多种方法算面积

相堂奎

学习了求多边形的面积之后，老师给同学们出了一道相关的题目：求下面组合图形的面积。

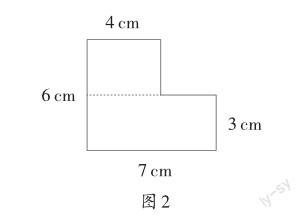
同学们思考片刻，纷纷动手算了起来。不一会儿，王艳同学举手发言说：“我是把这个多边形分成上、下两个长方形来计算的（如图2）。”

上面长方形的面积：4×（6-3）=12（平方厘米）

下面长方形的面积：7×3=21（平方厘米）

多边形的面积：12+21=33（平方厘米）

王雪同学也站起来发言道：“我是把这个多边形分成左、右两个长方形来计算的（如图3）。”

左側长方形的面积：6×4=24（平方厘米）

右侧正方形的面积：（7-4）×3=9（平方厘米）

多边形的面积：24+9=33（平方厘米）

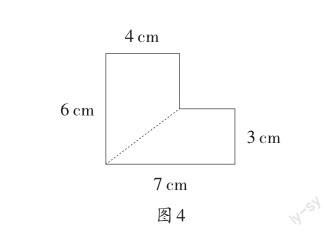
赵芬同学也举起了手，说：“我是把这个多边形分成两个梯形来计算的（如图4）。”

左上侧梯形的面积：（6-3+6）×4÷2=18（平方厘米）

右下侧梯形的面积：（7-4+7）×3÷2=15（平方厘米）

多边形的面积：18+15=33（平方厘米）

徐静同学起来发言道：“上面三名同学的算式虽然不同，但都是采用先分后合的方法，即合并求和。我是采用去空求差的方法，即先求出大长方形的面积，再求出小正方形的面积，最后求出多边形的面积（如图5）。”

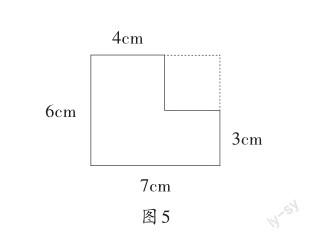
大长方形的面积：7×6=42（平方厘米）

小正方形的面积：（7-4）×（6-3）=9（平方厘米）

多边形的面积：42-9=33（平方厘米）

老师高兴地说：“同学们都有一双善于发现的眼睛，能思考出四种不同的解法！”聪明的你再想一想，看看还有其他的解法吗？