几类周期性delta 势的能带解
2024-01-10陆金成陈泽欢
陆金成,陈泽欢,王 晨
(1.苏州科技大学物理科学与技术学院,苏州科技大学江苏省微纳热流技术与能源应用重点实验室,江苏 苏州 215009;2.浙江师范大学物理与电子信息工程学院,浙江 金华 321004)
0 引言
在量子力学中,势能是一个非常常见并且重要的概念,许多基本问题都涉及了对于势能的讨论[1]。在量子力学的教学过程中遇到的最多形式的势能通常是方势能。而它的一种理想情况为delta 势。delta 势在教学与科研中频繁使用[2]。而采用了由delta 势所改进的量子粒子群-反向传播模型,则显著提升了BP 算法预测的精准度以及泛化性[3]。相比之前的模型,量子粒子群-反向传播模型所得到的误差也越小[4]。同样的,在研究非互易波二极管以及波的传播过程中[5],也通常会将非线性的交界面简化成一个delta 势来讨论,从而更好的解析得到波函数的表达形式。
在量子力学的教学过程中,接触过单delta 势的问题,由于delta 势所在位置的一阶导数不存在,由此推导出了delta 势所特有的一阶导数跃变条件,结合波函数的连续性得到了相应的波函数与能级表达式。本文从固体物理学中一经典例题出发[6],在单delta 势的基础上利用Bloch 波的形式讨论了周期性的单delta 势,Bloch 定理与单delta 势的解法相结合得到了相应的能带解析解。在这之后笔者不由想问周期性的双delta势。二维周期性的单delta 势等是否也能通过这样的方法解析解?于是本文就从推导单delta 势的解法出发,结合Bloch 定理得到周期性双delta 势的能带解析解,并画出相应的能带随势能强度,空间位置关系的图像。从中分析了能带性质。最后还讨论了二维周期性单delta 势的求解方法,它与一维周期性单delta 势的解密切相关[7]。
1 周期性的单delta 势求解
通常定态薛定谔方程的表达式如式(1)所示。
其中当V(x)=δ(x-a)V0时,V(x)δ 这样的形式就被称为delta 势。在教材中解决δ 势散射问题时通常采用的方法是利用波函数的连续性,以及波函数一阶导数的连续性。从而推导出本征解析解。然而δ 势的势能所在位置是一个奇点,其一阶导数是不连续的。因此在满足波函数的连续性的时,delta 势还需要推导相应的导数跃迁条件,才能获得其解析解。
首先从delta 势的定态薛定谔方程出发,如式(2)所示。
对于式(2),在一个无穷小的区间[a-∊,a+∊]中对薛定谔方程做积分,其中∊→1,如式(3)所示。
由于delta 函数的选择性,可以直接得到积分的结果,等式右边通过积分中值定理也可以化简得到式(4)。
其中ζ 取值范围为(a-∊,a-∊),等式两边取极限∊→0,可以得到delta 势的一阶导数跃变条件[7],如式(5)所示。
得到了delta 函数的一阶导数跃变条件,就可以结合波函数的连续性求解delta 函数的本征解析解。接下来讨论带有周期性的单delta 势,如图1 所示。

图1 周期性单delta 势垒
周期性单delta 势所对应的定态薛定谔方程如式(6)所示。
当x 取值为(0,a)时,V(x)=0,可以得到波函数如式(7)所示。
当x 取值为(-a,0)时,0<x+a<a,可以得到式(8)。
由于这个势具有周期性,可以把这里的波看作是Bloch 波,由Bloch 定理ψ(x+a)=eikaψ(x),如式(9)所示。
引入波函数的连续条件与delta 势的一阶导数跃迁条件。联立两个条件式子,如式(10)所示。
并化简得到k 和q 的关系式如式(11)所示。
从式(11)出发,画出了不同势能大小下的周期性单delta 势能级图,如图2 所示。
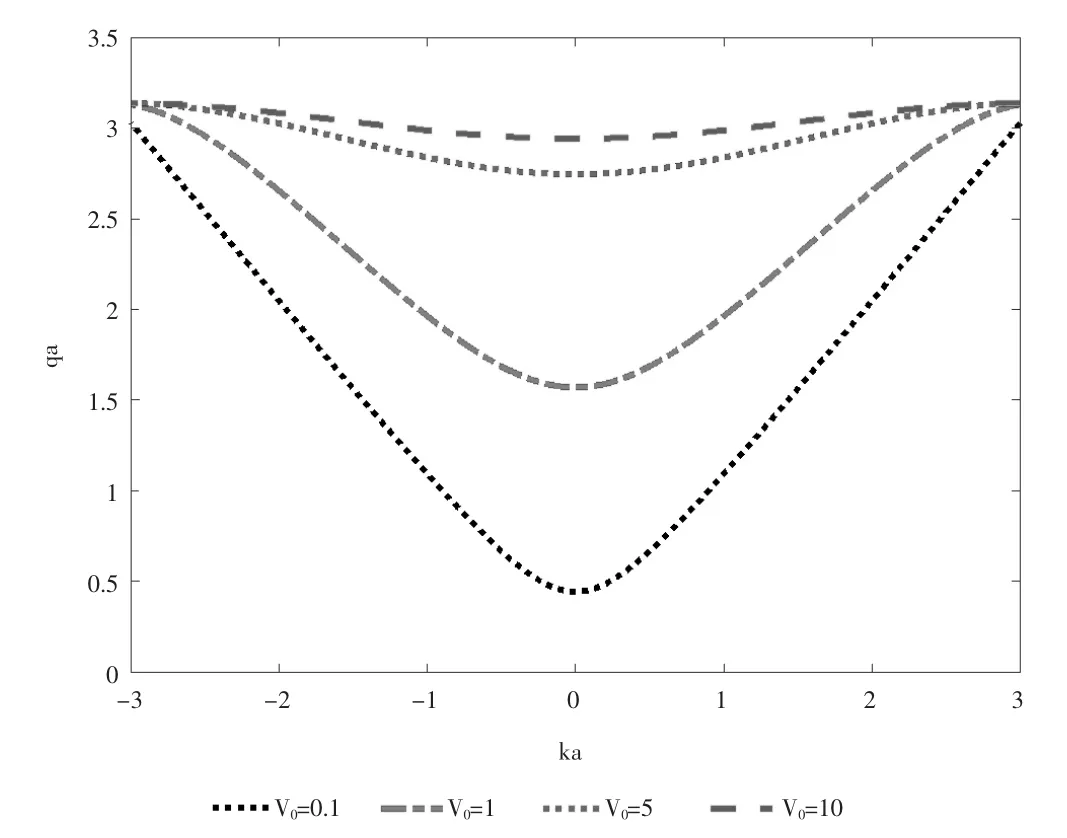
图2 周期性单delta 的能带图像
其中ka 代表波矢,(qa)2则正比于本征值,可以看出能级图是一个标准的偶函数。从式(11)看出,当V0=0时,k 与q 的关系是呈线性变化,反应出自由电子的特性。随着V0的引入,在k=0 附近,由于势能的影响,能带和自由电子行为差异很大。能量随V0的增大而增大。反观k=π 的附近,V0对能带行为产生的影响就越来越小。基于表达式,可以试着给出能带行为的描述,k=0附近时,假设q 的取值也在0 附近,这时式(11)第一项中的(sin q)/q≈1 是一个不可忽略的项。所以这时候V0散射就非常强烈,因此能带图像就与自由电子能带完全不一样。
2 周期性双delta 势求解
现在要考虑具有两个不同周期性的delta 势的能带图像,两个delta 势的空间位置a>b。在这样的情况下,薛定谔方程中表达如式(12)所示。
如同单delta 势的求解过程,我们首先列出不同区间的波函数表达,然后利用delta 函数的连续条件与Bloch 定理进行求解。
当x 的取值为(0,b)时,波函数如式(13)所示。
x 的取值为(b,a)时,波函数如式(14)所示。
x 的取值为(a,a+b)时,基于Bloch 定理,可以得到波函数如式(15)所示。
之后取x=a,x=b 两个交界面来求解波函数中的能级关系。
在x=b 的界面上,两边式子带入边界条件。
对式(16)进行化简,得到B,C 与A 的关系式。同理在x=a 的界面上,用边界条件也可以得到一组B,C 与A 的关系式,如式(17)和式(18)所示。
联立两个边界条件得到的关系式,并把A 在两边约去,得到只包含k,q 的关系式。其结果如式(19)所示。
这就是周期性双delta 势波矢与本征值的关系式,可以将得到的结果与周期性单delta 势的关系式进行比较。当V2≈0 时,式(19)变为式(20)。
发现这与周期性单delta 势的关系式是自洽的。
3 二维周期性单delta 势求解
二维周期性单delta 势,在一维的基础上利用分离变量法就可以求解。二维周期性单delta 势的薛定谔方程如式(21)所示。
利用分离变量法可以将哈密顿量进行两个维度上的分解,如式(22)~式(24)所示。
分离变量法,使两个维度上的波函数毫不相干,由此可以把一个二维的问题转化为两个一维的问题,直接就可以用周期性单delta 势的求解方法,如式(25)~式(26)所示。
式中:q1=,q2=。
4 结论
本文从固体物理教学中引入了具有周期性的单delta 势垒,结合delta 势的解析解法与Bloch 定理得到了相应的能带解析解。之后设想了一个周期性的双delta 势垒,用类似的方法进行了求解,并给出了相应的能带图像,并对能带行为进行了分析。发现在周期性delta 势场中,当k=0 时,delta 势的散射对于能带性质的影响较大。然而k=π 时,delta 势的散射影响就会变小。最后利用分离变量法解决了二维周期性单delta 势的问题。
