指数平均不等式及其应用

李玉佩

(汉寿县第一中学,湖南 邵东 415900)

对数平均不等式最近几年在高考中很活跃,很多文献都有介绍,甚至有些文献将对数平均不等式进行了深度的推广[1].而与对数平均不等式密切联系的就是指数平均不等式.笔者给出指数平均不等式的证明,并探究其与对数平均不等式的联系,最后给出指数平均不等式的应用.

1 指数平均不等式

2 不等式的证明

所以h(x)在(0,+∞)上单调递增,故h(x)>h(0)=0.得证.

这就是对数平均不等式,证明如下:

3 不等式的应用

例1已知f(x)=x-aex存在两个不同的零点x1,x2,证明:x1+x2>2.

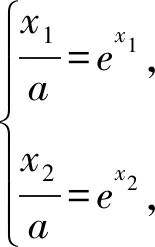
(1)若f(x)是R上的增函数,求a的取值范围;

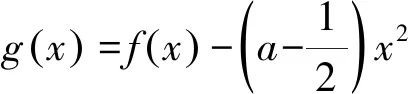
解析(1)a≤1.

这就是对数平均不等式,因此,x1+x2<2ln2a.

(1)若函数g(x)的图象与f(x)的图象关于直线y=x对称,且与直线y=kx+1相切,求k的值;

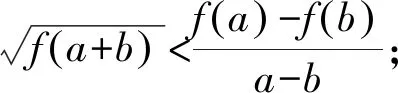
在两个结论中任选一个,并证明.(注:如果选择多个结论分别证明,按第一个计分)

(2)选择①:不妨设a>b,则a-b>0.

这就是指数平均不等式. 故结论①得证.

(1)证明:

①3

②函数g(x)有两个零点;

(参考数据:e≈2.72,e2≈7.39,e3≈20.09,ln2≈0.69,ln3≈1.1)

证明(1)①因为f′(x)=ex-1,当x>0时,ex>1,所以f′(x)>0,所以f(x)在区间(0,+∞)上递增.

因为x>0,a<0,所以ex-1>0,x-a>0,所以g′(x)>0,所以g(x)在区间(0,x0)上递增.

因为3

综上,g(x)存在两个零点.

(2)由(1)可知g(x1)=g(x2)=0,其中1

由g(x2)=0可知lnx2-a(x2+1)-x2lnx2=0.

设h(x)=lnx-a(x+1)-xlnx,则h(x2)=h(ex1)=0.

因为1e,x2>x0>3>e.

文中给出四道与ex有关的双变量问题的简便解法,让读者感受指数均值不等式的妙用,但是任何一种方法都有其局限性.我们在日常的学习中,要结合自身掌握程度和实际情况,选择最佳的解题方法,不可一味追求某一种解法,要学会从不同解法中汲取不同的数学思想,从而提高自身的数学核心素养与解题能力[3].