基于扰动观测器的无人机固定时间编队协同控制
2024-01-10贺林翰高晗威程鹏飞孙铭阳
贺林翰,高晗威,程鹏飞,孙铭阳,郭 永
(1.西北工业大学自动化学院,陕西西安 710129;2.西安现代控制技术研究所,陕西西安 710065;3.航天科工智能运筹与信息安全研究院(武汉)有限公司,湖北武汉 432200)
0 引言
近年来,无人系统的自主能力和智能化水平不断发展和提高,已经能够取代人类执行某些特定任务。无人机不仅广泛应用于任务侦察、目标打击等军事领域,还广泛应用于农业植保、遥感测绘、森林消防、影视航拍等民用领域[1-3]。随着无人机的应用越来越广泛,无人机所执行的任务也越来越复杂,任务难度也逐渐增加。单个无人机存在续航时间短、承载能力弱的缺点,这极大地限制了它的性能发挥,无法完成庞大的任务。在此背景下,多无人机协同控制与编队成为新的研究热点[4]。与单个无人机系统相比,无人机编队系统具有很多优点。例如,当无人机编队执行任务时,尽管编队中可能有一些无人机失败,但其他无人机可以继续执行任务,如此可以提高无人机完成任务的可靠性和效率。在无人机的编队控制中,需要使用一些编队控制方法,来完成多个无人机的协调控制,无人机的编队方法主要包括:领航-跟随方法[5-6]、虚拟结构法[7-8]、基于行为的方法[9]等。
无人机编队是1 个典型的多变量、强耦合非线性系统,而且在编队飞行过程中易受阵风等不确定外部扰动的影响。因此,提高无人机编队控制系统的鲁棒性和快速性至关重要。在各种干扰下提供准确稳定的编队控制是1 项具有挑战性的任务。到目前为止,大多数控制方法只能保证渐近或有限时间收敛,在这些方法中,收敛时间与初始状态有关。而在某些初始条件下,系统的收敛时间可能过长,这在工程实践中是不可接受的。文献[10]在研究双极限加权齐次系统稳定性的过程中发现了固定时间收敛特性。文献[11]对此进行了系统总结,提出了固定时间收敛的概念。固定时间收敛理论预先定义了1 个条件,即收敛时间与初始状态无关。这有效地解决了系统初值未知所带来的控制问题。现有的固定时间收敛研究主要集中在控制器设计和干扰观测器设计方面[12-14]。
基于固定时间收敛理论可使用各种控制设计方案设计控制器,以实现使系统固定时间稳定的目的。反步控制是1 种有效的非线性控制设计方案,它将原高阶非线性系统分解为不超过系统阶数的误差子系统,并利用李雅普诺夫稳定性理论计算控制律。文献[15]首先提出了求解非线性编队模型的反演控制方法,其基本思想是设计1个虚拟子系统的输入信号,并将其反馈给控制器,从而得到真实子系统的控制输入。该方法常用于无人机编队控制器的设计,并通过构造李雅普诺夫函数来验证其有效性。文献[16-17]将“leader-follower”方法应用于无人机的群体控制,将任意无人机作为“leader”,其他无人机作为“follower”;所考虑的问题可以简化为多无人机编队控制问题。然而,这种方法有一定局限性。文献[17-18]提出了虚拟领航者方法。他们将无人机视为刚体,每个无人机只能跟踪固定点并保持理想的队形。同时,文献[19]提出了基于行为控制方法的编队几何中心概念。此外,文献[20-22]采用基于“leader”的有向图协议共识方法,研究了多无人机的队形保持问题。
在控制器设计的过程中,为增强控制器的鲁棒性,基于扰动观测器的控制方法被提出,如模糊观测器[23-24]、非线性扰动观测器[25]、超螺旋观测器[26]、扩展状态观测器[27]等。超螺旋方法首先由Levant 提出,用于鲁棒精确微分[28]。超螺旋方法作为1种特殊的二阶滑模,具有不需要滑模变量导数信息的优点。文献[29-30]将超螺旋方法与其他智能控制算法相结合,进一步证明了其实用性。传统的超螺旋方法包括2个可调谐的固定增益,根据干扰的界来设计。文献[31]提出了1种多变量超螺旋滑模方法,但只实现了有限时间收敛。文献[32]通过对其进行修正,提出了1 种新的多变量固定时间的可重复使用运载火箭再入姿态控制方法。目前,国内对无人机编队的基于超螺旋观测器的固定时间控制研究较少。
综上分析,本文提出了1 种基于超螺旋算法的扰动观测器(super- twisting disturbance observer,STDOB)和固定时间反步控制(fixed-time backstepping control,FBC)的多无人机编队控制策略,并通过MATLAB 仿真软件对基于虚拟领航者的多无人机编队控制策略进行验证。相对于文献[31-32],总结出本文的关键创新点如下:
1)设计了1种基于超螺旋算法的扰动观测器,该观测器能够在固定时间内观测系统的外部时变扰动;
2)使用反步法解决无人机编队的固定时间控制问题,所设计的控制器实现了与无人机编队初始状态无关的固定时间收敛;
3)通过对扰动的精确观测,该控制器避免了传统自适应中对控制增益的过度估计,从而显著降低了抖振效应。
1 问题描述及预备知识
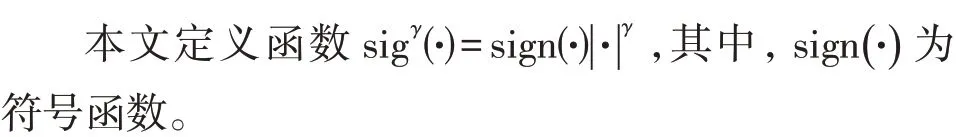
1.1 无人机单机及编队控制系统模型
考虑1 类含有外部扰动的无人机单机模型,第i架无人机的非线性运动学与动力学模型如下:

式(7)中:
为了构造编队误差模型,考虑1个由N架跟随者无人机与1 个虚拟领航者构成的多无人机系统,控制目标为:
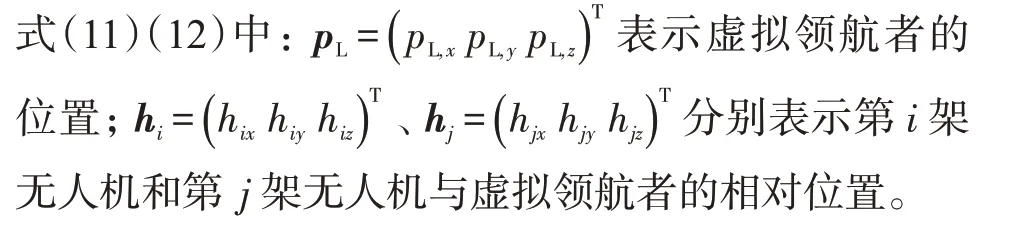
定义编队中第i架无人机的联合位置误差:
由上式可以看出,当联合位置误差ei收敛到0时,各无人机将按照预设的队形收敛到各自的期望位置,并形成期望队形。
定义编队联合位置误差与相对距离矩阵为:
则整个编队联合位置误差为:
定义:
则式(16)可以表示为:
对式(20)求导可得:
对式(21)求导并结合编队运动学与动力学模型,式(7)可得编队联合误差模型为:
式(22)中,d=。
令ė=ev,ev为编队联合速度误差,则式(22)编队联合误差模型可整理为:
本文的控制目标:针对一类含有外部时变扰动的无人机编队系统,设计1 种超螺旋干扰观测器观测系统的扰动;进而利用扰动信息设计反步控制器,使无人机编队能在指定时间跟踪上期望指令。
1.2 图论

1.3 预备知识
引理1[33]若有一连续径向有界函数为V:Rn→R+∪{0}符合以下条件:
1)V(x)=0 ⇔x=0;

则原系统能够在固定的时间内收敛到0,且对收敛时间T有:
注1 由式(24)可知系统的收敛时间仅由ϒ1、ϒ2、α、β决定,与系统的初始状态无关。
引理2[33]若有一连续径向有界函数为V:ℝn→ℝ+∪{0}符合以下条件:
1)V(x)=0 ⇔x=0;
2) 任 意x(t) 都 符 合 不 等 式V̇(x)≤-ϒ1Vα(x)-ϒ2Vβ(x)+ϑ,式中,ϒ1、ϒ2、α、β、ϑ都是正常数,并且0<α <1、β >1。
则原系统能够在固定的时间内稳定,且对收敛时间T有:
式(25)中,ϑ是满足0<ϑ <1的正常数。
引理3[34]若ε1,ε2,…,εM≥0,则有:
引理4(Yong’s Inequality)[35]对于∀(a,b)∈ℝ2,下列不等式成立:
式(27)中:ζ >0,Ψ >1,Φ >1,(Ψ-1)(Φ-1)=1。引理5[35]对于任意ι >0,x∈ℝ,存在不等式:
式(28)中,κ满足κ=,e 为自然常数,例如κ=0.278 5。
2 基于超螺旋算法的扰动观测器设计
针对无人机编队系统,设计了基于超螺旋算法的具有定时收敛特性的扰动观测器(STDOB),可以补偿等效扰动。此外,还分析了扰动观测误差的收敛时间。无论初始状态如何,该扰动观测器都能在有限时间内将估计误差收敛到原点的小邻域内。观测器的设计结构如下:

定理1 构造的扰动观测器(29)可以在固定时间内对外界扰动d精确估计,且观测误差σ为0。
证明对σ求导,可以得到:
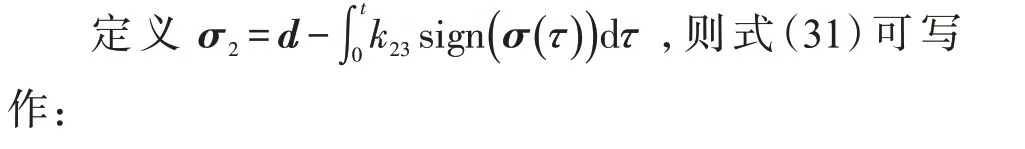
接着计算σ2的导数,可得:
由式(32)(33)可得误差如下:
基于文献[36]的结论,如果观测器的增益满足条件(30),则σ̇和σ̇2可以在固定时间t0内收敛到原点,且有:
则可得,当t≥t0时,σ=0,σ2=0。回顾式(31)可得σ̇=d-d̂=0,即d̂=d。因此,t≥t0之后,观测器可以精确地估计等效扰动,即可以实现固定时间扰动观测,证毕。
3 固定时间反步控制器设计
根据前文中建立的无人机编队模型以及所设计的固定时间扰动观测器,设计虚拟控制量evd和固定时间反步控制器F为:
定理2 考虑模型为式(23)的基于联合误差的无人机编队误差模型,设计基于扰动观测器(29)的固定时间反步控制器(37),可实现无人机编队控制,且闭环系统中所有的信号都是固定时间稳定的,编队联合位置误差e和编队联合速度误差ev在固定时间tm内收敛到0,且tm满足tm≤t+t0,t将在后文给出。
证明定义:
设速度误差与虚拟控制量的误差为:
构造李雅普诺夫函数:
对式(40)求导得:
将式(37)代入式(41)得:
由Young’s不等式(引理4)可知:
代入式(42)得:
对向量z1中的元素z1i(i=1,2,…,N)的值分情况讨论。若z1i >1,
若z1i <1,
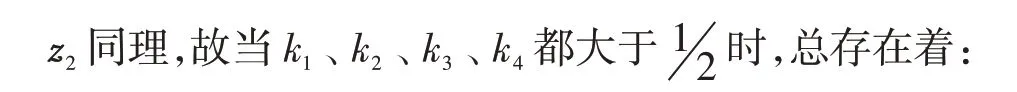
由引理5整理得到:

4 仿真分析
4.1 仿真条件
为了验证设计控制方案的有效性,在本文提出的控制器下对无人机编队飞行任务进行了数字仿真。仿真中的无人机编队包含3架实际编队飞行的无人机和1架虚拟领航无人机,所有无人机的初始信息如表1所示。无人机编队队形为以虚拟领航无人机(编号0)为中心,3架无人机(分别编号1、2、3)为3个顶点的等边三角形。在编队中,设计的队形中其他无人机与虚拟领航无人机的期望相对距离如表1 所示;编队中各个成员的初始参数如表2所示。
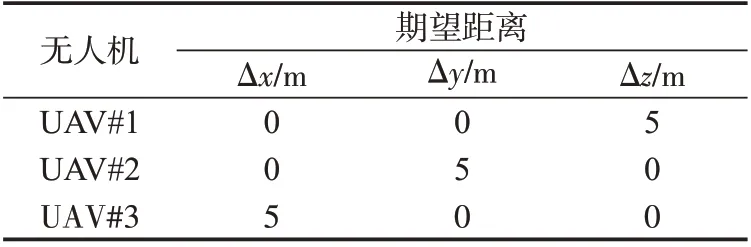
表1 无人机编队队形Tab.1 UAV formation
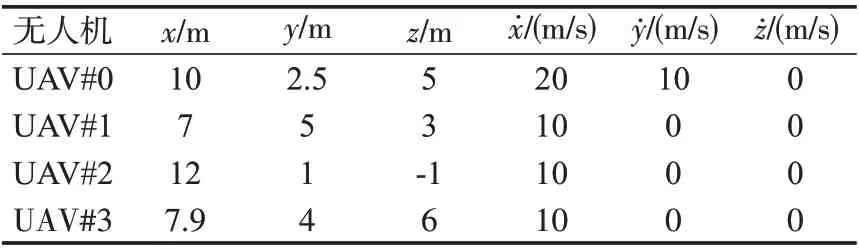
表2 无人机编队初始参数Tab.2 Initial parameters of UAV formation
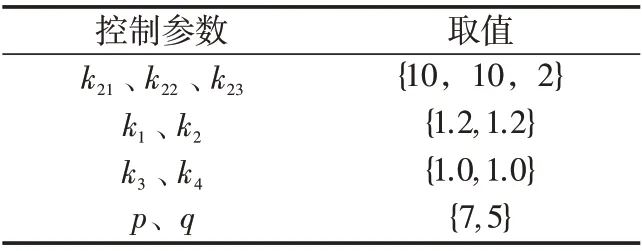
表3 控制参数Tab.3 Control parameters

4.2 仿真结果
图1为编队中3架无人机基于编队模型建立的编队联合位置误差。在设计的基于固定时间超螺旋干扰观测器的多无人机反步控制器的作用下,联合位置误差的跟踪曲线光滑且无超调,并且无人机#1的稳态误差在0.1 m 以内,其余2 架无人机的稳态误差在0.01 m 以内。
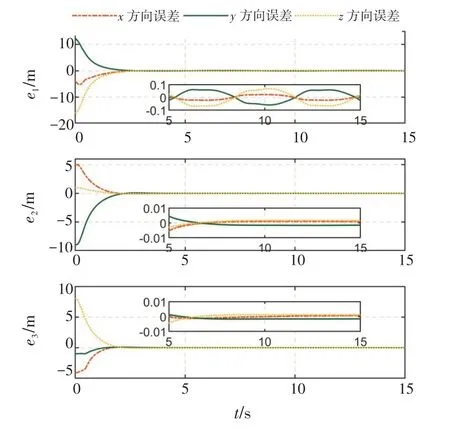
图1 无人机联合位置误差Fig.1 Joint position error of UAVs
图2 为3 架无人机的联合速度误差。可以看出,联合速度误差以较快的速度收敛,且无人机#1的稳态误差保持在0.15 m/s 内,其余2 架无人机的稳态误差在0.05 m/s以内。
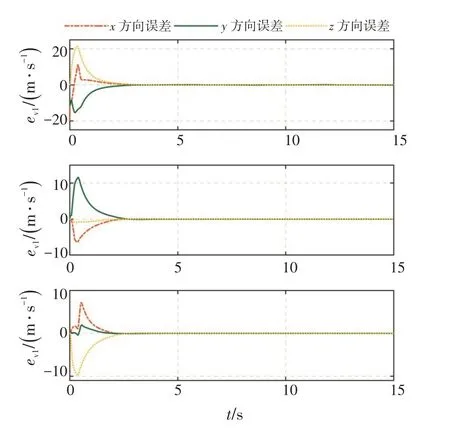
图2 无人机联合速度误差Fig.2 Joint speed error of UAVs
图3为3架无人机的实际上与自身在编队中的理想位置的绝对位置误差。可以看出,其收敛的时间与联合位置误差是一致的,且收敛过程无超调,稳定误差在0.1 m以内。
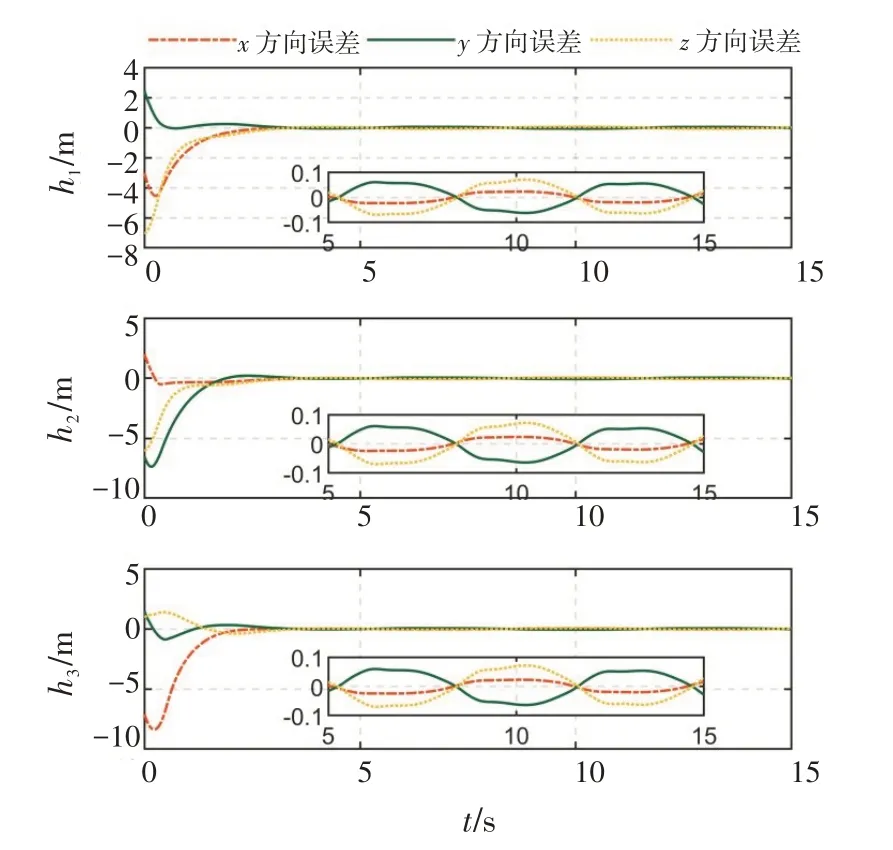
图3 无人机绝对位置误差Fig.3 Absolute position error of UAVs
图4为3架无人机的3个方向的控制力变化情况,控制力的输入有最大限制。系统在3个方向上存在正弦波形式的扰动,因此控制力也呈现一定的波动来抵消扰动,且控制力在波动的过程中保持在输入限制以内。
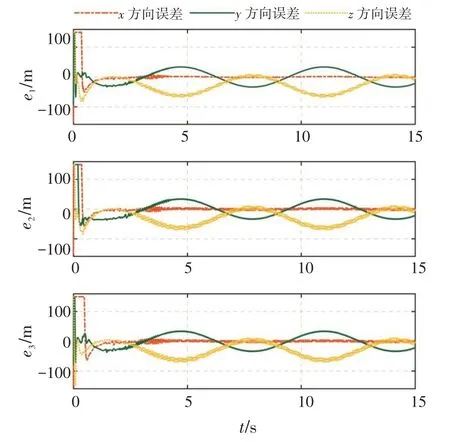
图4 无人机控制力Fig.4 Control force of UAVs
综上所述,基于本文所提出的超螺旋干扰观测器,可对系统中存在的外部扰动进行固定时间内的快速准确的估计。基于固定时间超螺旋干扰观测器的多无人机反步控制系统,可使无人机编队在固定时间内组成期望队形,并跟踪上虚拟领航无人机的轨迹。
5 结论
本文提出了1种基于固定时间超螺旋干扰观测器的多无人机反步控制系统。针对含有外部扰动的多无人机编队系统,基于超螺旋干扰观测器和反步法理论设计了固定时间控制器,使得系统的多架无人机能在指定时间内跟踪上期望的指令信号。最后,数值仿真结果证明了本文所提出的控制方法的可行性与先进性。
