多仓库下物流无人机协同配送方法

杜鹏飞，何 翔，张学军，2

（1.西华大学航空航天学院，四川成都 610039；2.北京航空航天大学电子信息与工程学院，北京 100191）

0 引言

随着电子商务快递业的快速发展，物流配送量与日俱增。当前，传统的地面车辆配送很难在短时间内配送大批量的包裹，且车辆易受到地形的影响，使得配送成本和配送时间大大增加。在此背景下，物流无人机逐渐兴起，并具有巨大的发展前景[1]，它可以有效提高配送效率。但大多数无人机存在电能不足、续航时间短等问题[2-3]。因为在物流配送中，为提高配送效率、减少配送成本，就需要进一步考虑任务协同分配[4]。所以，科学规划配送路线变得尤为重要。

在针对无人机配送建模中，大多是对无人机飞行范围、飞行时间等进行简单约束，构建的模型无法满足实际的配送需求。因此，精确估计载重、能耗等因素对于配送的影响至关重要。当前，很多研究者[5-8]在进行无人机路径优化过程中，充分考虑了路径长度、安全风险以及燃料损耗等目标，并通过加权求和，将这些目标转化为单目标问题。

文献[9]提出无人机和卡车存在同一个配送网络的问题，在建模中综合考虑了载重的变化。在对多仓库配送问题的解决方案中，文献[10]构建了1 个新的整数线性规划模型，该模型允许在目标函数内体现仓库位置和路线的优化。文献[11]考虑了不同仓库间车辆的共享，得出共享的车辆资源可以潜在地减少交付距离和燃料消耗。文献[12]提出了K互连多站多旅行推销员问题，并提出了1 种基于超启发式的人工蜂群算法。文献[13]采用边界分配法将该问题转化为单仓库车辆调度问题，并结合遗传算法（Genetic Algorithm，GA）与蚁群算法求解跨区域配送最优调度方案。文献[14]用聚类分析最短距离分配法，将多仓库车辆调度问题动态地分解为多个单仓库车辆调度问题进行求解。针对求解规划问题时存在易陷入局部最优的问题，文献[15]在求解无人机路径的基础上，基于传统PSO 的基础上，引入细菌觅食算法，有效提高了寻优能力。文献[16]针对传统的粒子群优化算法容易陷入局部最优解的问题，提出了1 种自适应粒子群优化算法，在迭代寻优过程中自适应地调节惯性权重和2个学习因子的数值。文献[17]针对多基地无人机协同规划航迹计算复杂、容易陷入局部最优的问题，在GAPSO的基础上，引入禁忌搜索算法混合为GAPSO-TS算法。文献[18]提到了基于深度学习和强化学习的任务分配研究在未来研究中的趋势。

当前的研究中，针对建模，各个模型考虑的因素有限，无法贴合物流配送真实场景。同时还需注意到，针对算法的改进，主要是通过改进操作算子以及融合其他算法以提高算法的搜索能力，进一步获取成本更优的配送方案。基于此，本文在允许无人机携带多个包裹的情况下，考虑了无人机的能耗变化、顾客混合时间窗以及同时取送货情况，构建多仓库物流配送模型。考虑到GA存在收敛速度慢的问题，基于GA引入LNS（Large Neighborhood Search Algorithm，LNS）用作局部搜索算子提出基于改进GA（Improved GA，IGA）的物流无人机协同配送算法，利用GA 的全局搜索和LNS局部搜索的优化机制进行求解，进一步获取最优配送方案。

1 配送问题建模

1.1 问题描述

设定某城市区域存在多个仓库和若干个顾客需求点，引入移动充电桩给物流无人机更换电池以提高无人机的飞行时长。在配送的过程中，可以到距离最近的充电桩充电。本文做以下假设。

1）网络中包含两类节点：第一类是仓库，仓库是无人机的出发和返回点；第二类是顾客点，每1个顾客都包含服务时间窗、服务时间、包裹需求以及寄送量等需求。

2）顾客的时间窗设定为混合时间窗模式，该模式包含软时间窗和硬时间窗。

3）针对顾客的取送货情况可分为3种情况，分别是同时有取货和寄货需求的顾客、只有取货需求的顾客以及只有寄货需求的顾客。无人机对3种类型顾客的服务时间不同。

4）无人机在配送过程中处于耗能状态，耗能速率随着载重而变化。

5）无人机的出发和返回配送站可以不同。

1.2 模型构建

1）参数与变量。本文涉及的参数如表1所示。

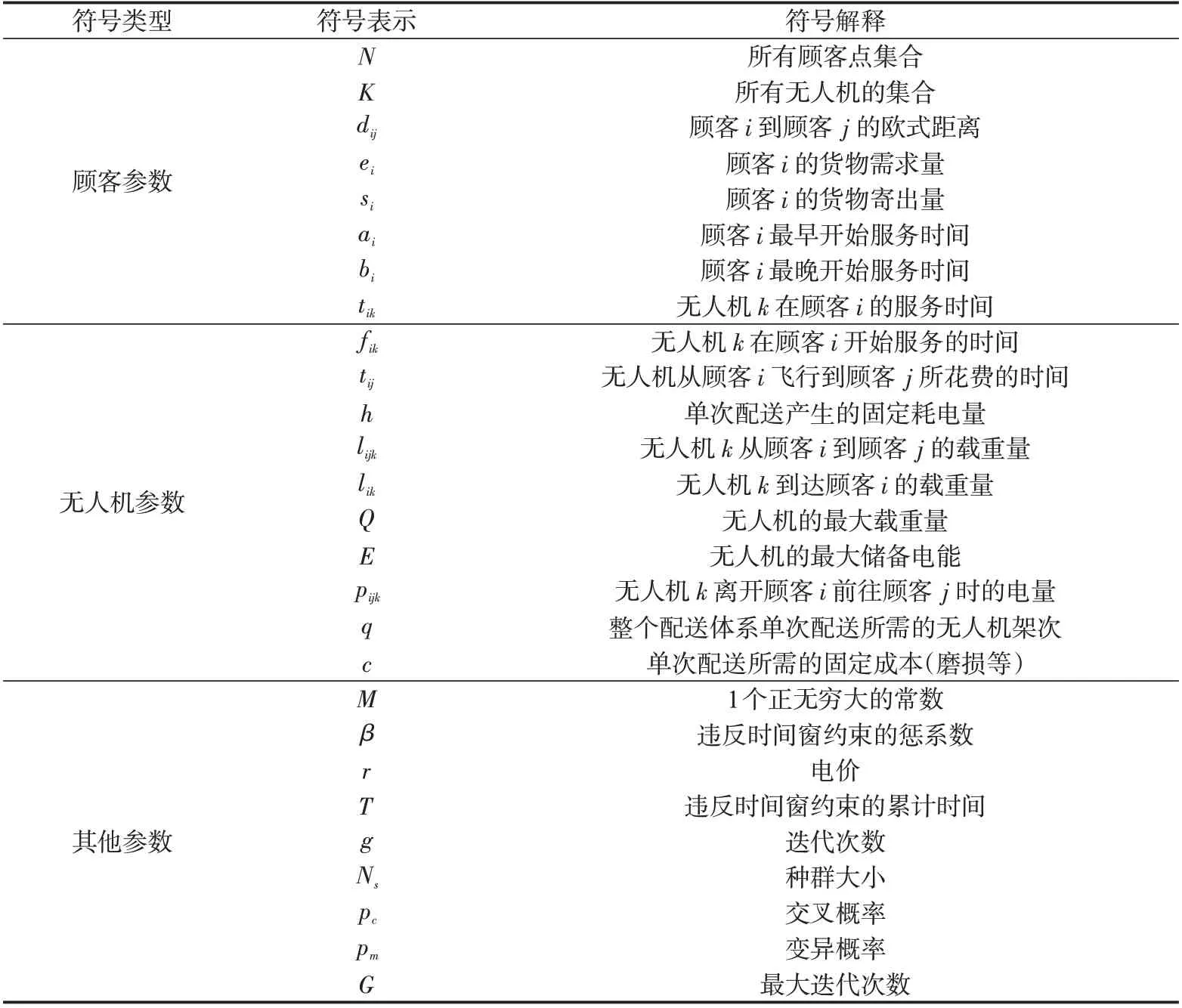
表1 参数定义Tab.1 Parameter definition

2）目标函数。本模型以优化经济成本为主，其中，根据无人机配送能量消耗过程建立模型[19]，电池功率表示为：

式（1）中：Pij为无人机从顾客i到顾客j时的飞行功率；W为无人机本身质量；l为无人机的载重；vij为无人机从顾客i到顾客j的速率；η为螺旋桨动力传递效率；γ为无人机升阻比；e为无人机电子元件能耗。考虑到电子元件耗能所占比重较小，因而在本文中不予考虑。

本文假设无人机以恒定速率飞行，则无人机从顾客i到顾客j之间消耗的电能可以表示为：

物流无人机协同配送的总目标是使得物流配送产生的成本最小，目标函数为式（3），其中：第1项为无人机在配送过程中的能耗成本；第2 项为无人机单次飞行的固定成本；第3 项为无人机违反顾客时间窗的惩罚成本。

3）约束条件：

针对无人机的约束，式（4）为0、1 变量，表示对于无人机k、顾客i与顾客j的路径是否联通；式（5）表示i点完成飞行的无人机数量等于在i点开始飞行的无飞机数量；针对载重的约束，式（6）表示每1 架无人机的载重量不得超过其最大载重；式（7）为保证无人机在2个顾客之间的载重约束；式（8）表示无人机从仓库出发时的载重为所经顾客的送货量之和；式（9）表示无人机返回仓库的载重为所经顾客的寄货量之和；针对时间窗的约束，式（10）（11）表示节点与节点之间的到达时间的关系；针对电能的约束，式（12）表示无人机在顾客点的电能均应小于最大电能E；式（13）表示无人机在2个顾客之间的飞行能耗剩余值之差等于其飞行过程中产生的能耗之和；式（14）表示无人机离开顾客i时的电能必须保证其到达顾客j。

2 算法设计

针对各种启发式算法的特点，本文使用基于GA对所提模型进行优化求解。基于GA与LNS的各自特点，在GA 中引入LNS 作为局部搜索算子，提出基于IGA的物流无人机协同配送算法

2.1 初始解的构造

在遗传算法中，初始解的构造是操作算子的基础，其使用实数进行编码，规则如下。

1）将顾客随机排列，按照序列依次添加客户点。

2）判断添加的顾客点是否满足无人机载重约束和顾客时间窗约束。若不满足，则判断是否能够直接添加仓库；若可以直接添加仓库，则添加仓库。

3）在判断无人机满足载重和顾客时间窗约束后，继续判断是否满足能耗要求。若能耗要求被满足，则直接将顾客点加入解码序列之中。

4）当该路径不符合载重约束或者能耗约束，则储存该条路径，同时新增无人机架次。

重复上述步骤，直到将每个顾客点都加入编码之中。考虑仓库会随着顾客分布而变化，因而在该解码序列中，仓库先不加入。在解码时，使用最近邻插入法，单独获取每1条路线的所属仓库，进一步计算目标函数值。

直接编码法[20-21]是将充电桩直接编入染色体编码中。在本模型中，即将无人机经过的所有顾客和充电桩都编入染色体编码中，但考虑到仓库的特性，不将其编入染色体编码，而将其以1 个符号表示。该编码流程较为直观，考虑了场景中各个元素，无须后期再插入充电桩。但是该方法也存在缺陷，最优的充电桩位置会随着算法的迭代而改变，甚至会出现配送路线无法满足约束条件。

最近插入法[22]表现为充电桩编码不参与直接编码。在编码中，只编入仓库和顾客的编码。在解码时，再考虑向配送方案中结合能耗需求选择最合适的充电桩。解码后的配送方案是否满足载重约束以及时间窗约束，还需进一步判断。该编码中，插入位置为没有充足电能的位置，无法在全局层面实现插入最优。

基于最近插入法提出综合插入法，即考虑到插入位置的全局最优，即不局限于向电能不足处插入充电桩，而是从整条路径出发，选择最合适的插入位置和充电桩。

2.2 局部搜索

考虑到遗传算法在求解模型的过程中收敛速度较慢，为提高算法搜索速度，在遗传算法的基础上加入局部搜索算子。本文引用了LNS的相关概念，通过移出和重新插入2 个过程，对染色体进行局部搜索。LNS包含破坏（Destroy）算子和修复（Repair）算子。破坏算子的作用是采用相关性原则从当前个体中移除若干个顾客；修复算子的作用是在满足载重和时间窗约束的前提下，将移除的顾客插回到使车辆行驶总距离增加最少的位置。若修复后的个体成本小于破坏前的个体成本，则用修复后的个体替代破坏前的个体。

2.3 算法流程

IGA 流程为：随机生成初始种群，再进行选择、变异、交叉和局部搜索。IGA的流程如图1所示。

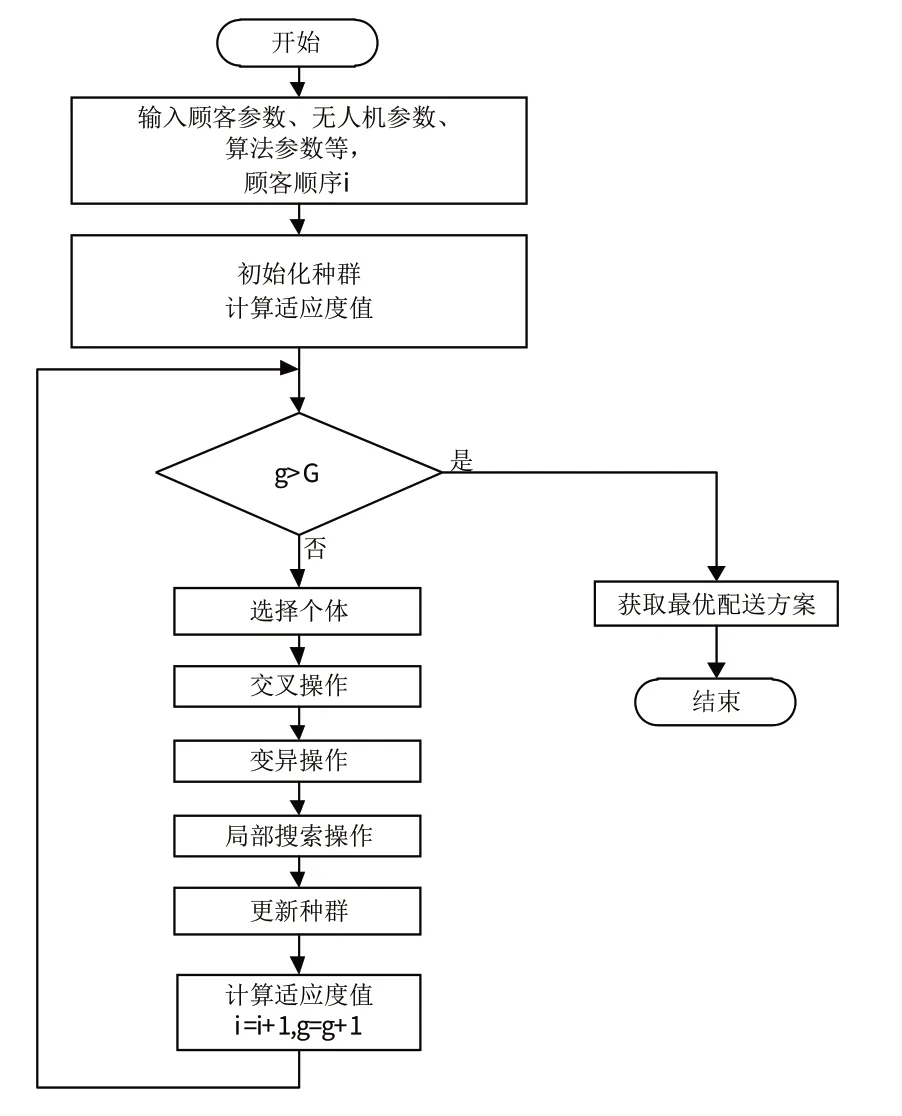
图1 IGA流程Fig.1 IGA process

3 仿真及结果分析

3.1 仿真测试pm

为验证模型和算法的有效性，结合算法对模型进行优化求解。为了能够直观地展示本文仿真试验结果，本节以顾客数量为50 的配送优化方案为例。其中，顾客位置按照均匀分布随机生成，送货量在小于无人机最大载重范围内随机生成，服务时间窗参考Solomn 数据C101 进行设定。本模型中，参数设置如表2所示。顾客、仓库和移动充电桩分布如图2所示。

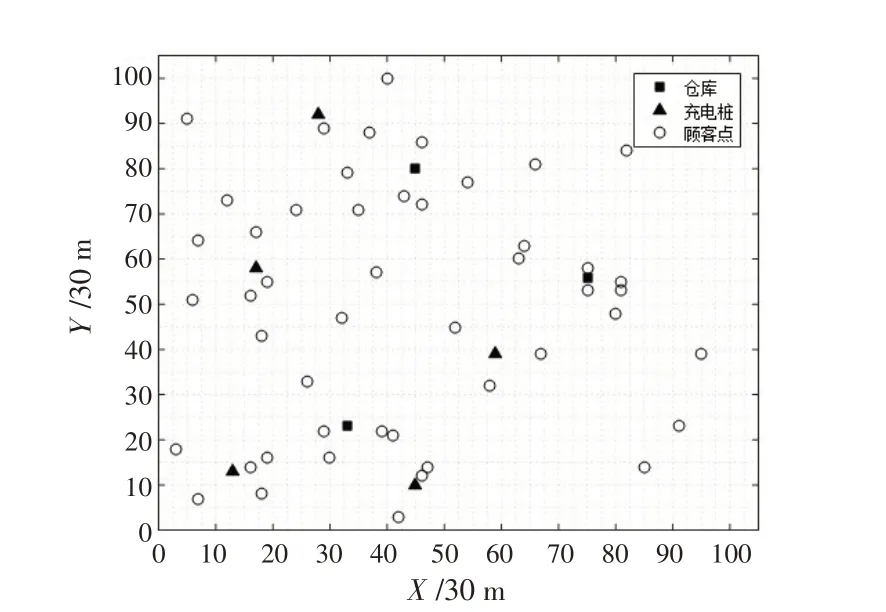
图2 仓库和充电桩分布图Fig.2 Distribution of warehouse and charging station

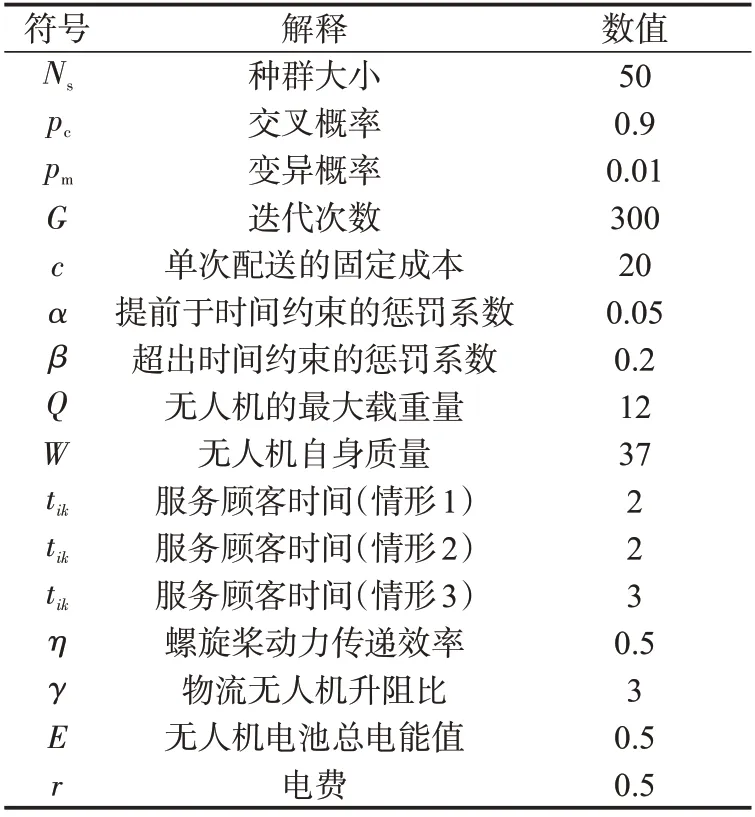
表2 模型参数值Tab.2 Model parameter value

本模型使用IGA和GA同时对模型进行求解获取最优配送成本。为寻找最佳任务分配方案，取20次重复仿真实验中算法适应度值最小的1 次实验结果，绘制其对应的迭代曲线如图3 所示。从图3 可以看出，通过对比算法获取最优配送成本，该算法在初期就显示出较快的收敛速度。在迭代200次时便已经得到了较好的结果，表现出了较强的搜索能力。图3中，IGA获取的最优配送经济成本为3 023元，GA为3 264元，IGA 较GA 显著降低了配送经济成本（降低了7.38%）。可以说，IGA在降低物流配送成本方面具有明显的作用。经检验，各架无人机均满足自身能耗和载重约束要求，进一步验证了算法的有效性。获取种群平均配送成本变化值，如图4所示，平均成本在前期下降之后，相对稳定。可以得出，该算法对于种群的优化效果是显著的。

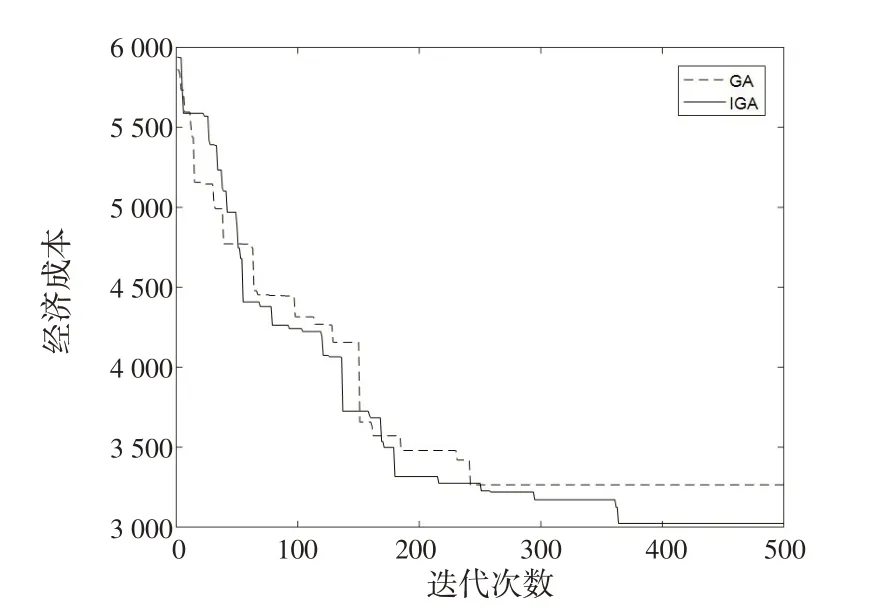
图3 经济成本优化过程Fig.3 Economic cost optimization process

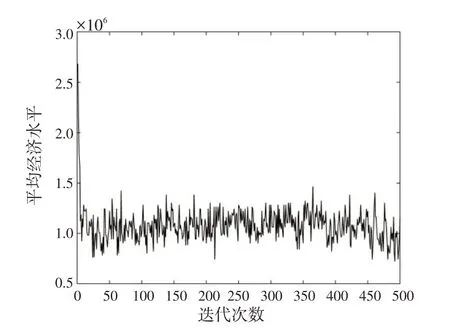
图4 平均成本变化图Fig.4 Changes in average cost

在此条件下，进一步获取种群的平均配送距离变化值，如图5所示。

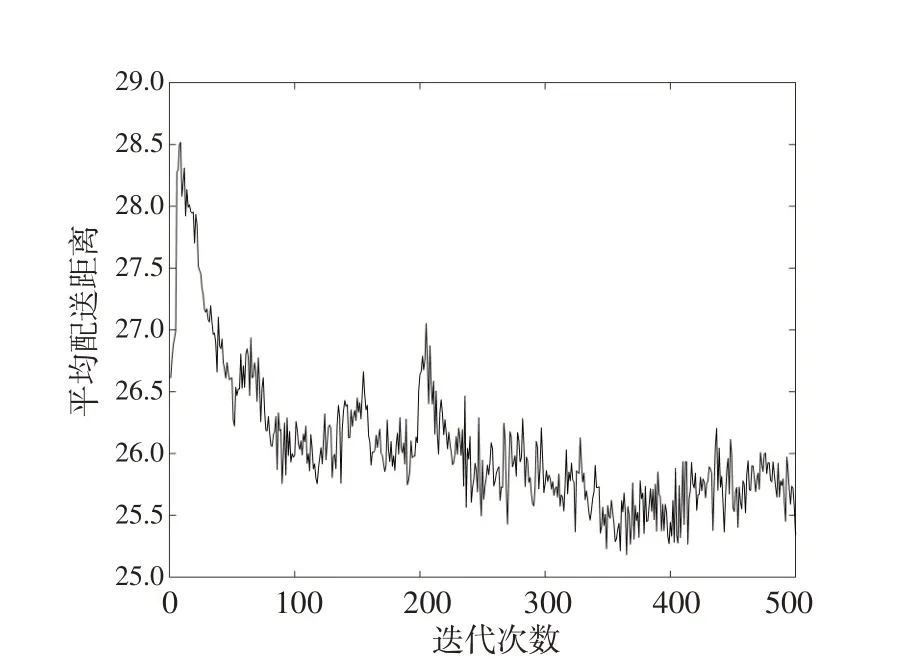
图5 平均配送距离变化图Fig.5 Change in average distribution distance

由于在优化过程中配送距离并非首要优化目标，因而在优化过程中的浮动相对较大，这是因为影响配送经济成本的因素不只有配送距离，还有违反时间窗总时长，但同时配送距离可以直接影响到配送经济成本。随着迭代次数地增长，种群平均配送距离呈现随着迭代过程逐渐下降且逐渐趋于平稳的过程。

3.2 Solomn数据验证

为验证上述方法的有效性，用所提方法IGA 对Solomn数据集进行仿真测试。在此测试中，考虑到数据集顾客需求与原设定无人机最大载重不相符，故设定无人机最大载重为60 kg，测试10 次取其平均值记录于表3。通过求解不同规模算例发现，在同一个算例系列中，随着顾客点比例增大，无人机的配送成本呈上升趋势。通过无人机的使用量发现，同一个算例系列中，随着顾客点比例增大，无人机数量有所增长。通过将IGA 与GA 的求解结果进行对照，进一步验证了所提算法的有效性。同时，在数量较少的算例中，各个算法求解的最优成本几乎一致，随着顾客数量增多，IGA求解效果更加显著，即该算法获取的最优配送成本。

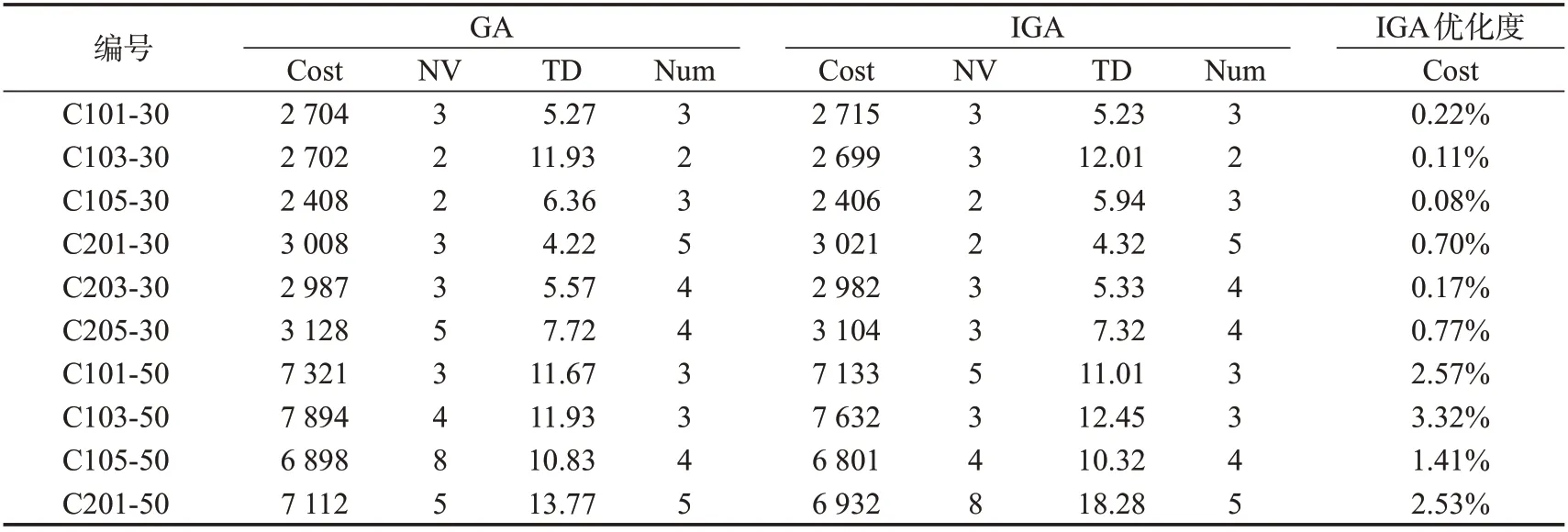
表3 Solomn数据验证结果Tab.3 Verification results of solomn data

4 结论

本文基于城市区域无人机配送场景，构建了以经济成本最小为目标函数的多机协同任务分配模型。为提高GA 的寻优能力，在GA 的基础上加入LNS 局部搜索算子，进而提出IGA 对所提模型进行寻优求解。仿真实验表明，基于IGA的物流无人机协同配送算法可以有效实现多目标优化，适合解决城市环境下多仓库的任务分配问题。同时，为进一步明确算法的有效性，通过引入Solomn进行测试，仿真结果显示，所提IGA可以有效降低物流配送成本。