基于Nussbaum函数的多无人机预设性能反步容错协同控制

孙朋悦，杨海川，李嘉旭，余自权

（南京航空航天大学自动化学院，江苏南京 211106）

0 引言

无人机在军用与民用领域作为日益重要的空中力量，被广泛用于植物保护、森林防火、巡检变电设备、智能物流调度、应急救援、空中作战等领域。多无人机对海上舰船作战是无人机应用的研究热点[1-6]。在集群无人机远航作战中，利用多机的高效率和高可靠性优势，部署多架无人机可满足海上侦察巡视、防卫干扰、火力打击等作战任务需求，然而复杂多变的海洋环境和执行器故障极易导致机间碰撞，对无人机的稳定性与安全方面会产生极大影响。未来多机协同完成任务过程中的安全性与可靠性会更加重要。

反步法是1 种递归过程的设计方法，可通过递归的方式构建出最终控制信号。由于反步法中会涉及虚拟控制变量微分的计算，致使反步法存在微分爆炸问题，而动态面控制可作为解决这一问题的有效途径之一。文献[7]针对同时存在执行器、外界干扰和多个未知控制方向的多输入多输出非线性系统，将模糊逻辑系统与反步技术相结合，利用Nussbaum 函数解决了控制增益方向未知带来的问题。在多无人机协同过程中，误差会通过通信拓扑传递给相邻无人机，可能导致整个集群系统的不稳定甚至无人机之间发生碰撞，对多机协同的稳定性与安全性造成巨大的影响，因此要求误差限制在一定的范围内。为使误差收敛在期望的范围内，研究人员提出了许多约束控制方案，如障碍李雅普诺夫函数、预设性能函数等。文献[8]针对扰动下的复合式变体无人机，设计了复合时变障碍李雅普诺夫函数和动态滑模面的控制方法。预设性能控制是1 种被广泛使用的控制算法，通过将系统的输出误差约束在期望的范围内，可使跟踪误差收敛到1 个小的残差集中，并同时兼顾了系统的瞬态与稳态性能。文献[9]设计了1 种具有预设性能的高速飞行器的自适应反步控制方法，并利用径向基神经网络逼近了高速飞行器的不确定项。

受文献启发，针对多无人机协同执行任务过程中可能遭遇执行器故障的问题，本文主要贡献如下：

1）与文献[10]处理故障的方法相比，本文基于Nussbaum 函数处理由故障引起的未知控制增益的问题，设计了分布式预设性能反步协同容错控制方案，降低了控制算法的复杂度，在多无人机遭遇故障时保证了系统协同执行任务的安全。

2）与文献[11]预设性能控制设计方法相比，由于故障率先对角速率产生影响，继而对姿态产生影响，因此设计了2 种预设性能函数。首先，约束角速率误差，保证无人机自身实际角速率跟踪上虚拟控制信号的角速率；然后，进一步约束无人机和相邻无人机之间的协同姿态跟踪误差，收敛到任意小的1个区域，且均满足期望的超调量与收敛时间，抑制了故障对系统造成的不利影响，以提升系统的容错性能。

1 问题描述与预备知识

1.1 UAV运动模型

本文面向由N架固定翼无人机构成的飞行编队，开展容错协同控制方案设计。第i架无人机力学方程表示为[12]：

式（1）中：i=1,2,…,N；mi和gi分别为无人机质量和重力；Vi、χi和γi分别为空速、航向角和飞行路径角；αi、βi和μi分别为迎角、侧滑角和航迹倾斜角；Ti、Di、Li和Yi分别为推力、阻力、升力和侧向力。

无人机姿态运动学模型表示为：

式（2）中：pi为滚转角速度；qi为俯仰角速度；ri为偏航角速度。

无人机的姿态动力学模型表示为：

式（3）中：ℒi、ℳi和Ni分别为总力矩在机体坐标轴系上的分量，即滚转力矩、俯仰力矩和偏航力矩。

式（2）中的推力Ti、空气动力Li、Di、Yi，式（3）中的空气动力力矩ℒi、ℳi和Ni表示为：

考虑增益损失故障，执行器故障模型为：

将式（7）故障代入姿态模型，可得：

将xi1求二阶导可得：

式（9）中，Fi=fi1+gi1xi2+gi1fi2,Gi=gi1gi2。

定义跟踪误差：

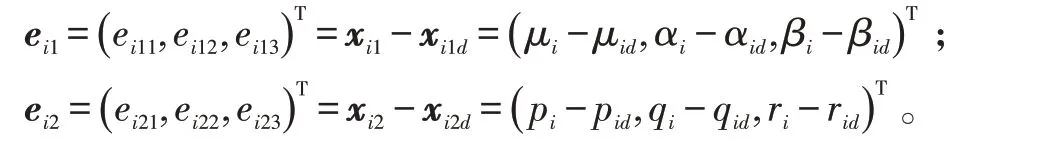
为了实现多架无人机的同步跟踪控制，定义如下分布式同步跟踪误差：

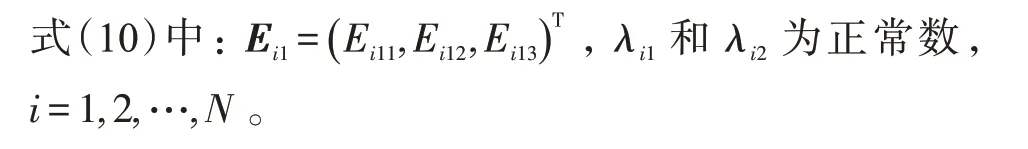
进一步，分布式同步跟踪误差可以化为：

1.2 预设性能

定义1 如果1个平滑函数ϖ(t):ℝ+→ℝ+能够满足以下条件，则称为预设性能函数[16]：

1）ϖ(t)是严格单调递减的正函数；

根据定义，选择如下预设性能函数[17-18]：

式（12）（13）中：εi1τ0、εi1τ∞、νi1τ、νi2τ、ιi1τ和εi2τ∞为待设计的参数；i=1,2,…,N，τ=1,2,3。显然，所选函数εi1τ(t)和εi2τ(t)满足预设性能函数的定义。

跟踪误差Ei1和ei2分别满足下述不等式：

其中：

式（16）（17）中，κi1τ=0.5 ln()。Γ(·) 是光滑的严格递增函数，存在下列特性：

1）Γ( 0)=0；

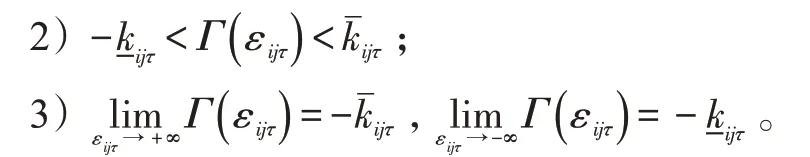
其中，j=1,2。

转换后的误差可以表示为：

进一步求导可得：

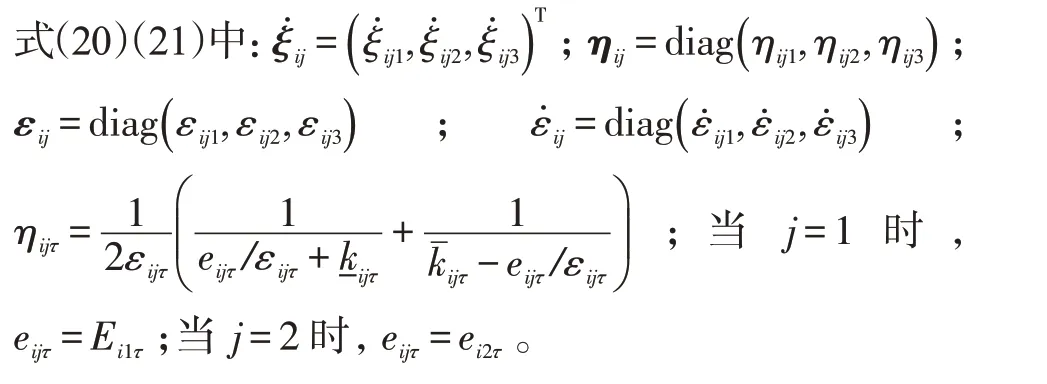
1.3 Nussbaum函数

定义2 如果函数N(ζ):ℝ →ℝ 具有如下的性质，则称其为Nussbaum函数：

选择偶函数ζ2cos(ζ)作为Nussbaum 函数来设计系统的控制器。

引理1 给定1个Nussbaum函数N(ζ)，则：

1）对于任意1 个有界的函数g(·):ℝn→ℝ，满足|g(·) |∈[ε0,g0)成立，其中ε0是任意的正的常数，g0是1个未知的正的常数且有ε0＜g0＜+∞成立，那么就是说g(·)N(ζ)也是Nussbaum的函数；

2）对于任意1 个函数如果满足c(·) ∈[-ε0,ε0]⊂ℝ成立，就说N(ζ)+c(·) 也是1个Nussbaum的函数。

引理2 设V(t)≥0，且ζ(t)是定义在[0,tf)上的光滑函数，同时函数N(ζ(t))是1 个偶的光滑Nussbaum 函数，如果下面的不等式成立[21]：

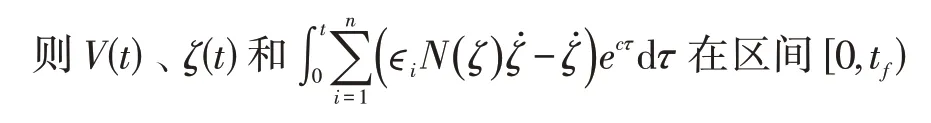
2 容错协同控制器设计

2.1 控制器设计

本节提出了基于Nussbaum 函数的预设性能反步容错协同控制方案，依据反步法，第i架无人机的中间虚拟控制信号设计为：

式（24）中：Λ=λi1+λi2ℒii；K1为待设计的参数。

基于Nussbaum函数，构建如下控制信号：

式（25）～（28）中：N(ζ)=diag(N1(ζ1),N2(ζ2),N3(ζ3))；K2为待设计的参数，ϑi的表达式如下：

式（29）中，K为待设计的参数。

2.2 稳定性分析

证明：选取Lyapunov函数为

对式（30）求一阶导数并代入式（6）（8）（11）（20）（21）（24）和（28）可得：

式（31）中：κi=2 min{λmin(K1),λmin(K3)}；υi=gi2ρi。

式（31）左右两边同乘以eκit，可得：

3 仿真结果及分析

为了验证本文预设性能反步容错姿态协同控制方法的可行性，对4 架固定翼无人机组成的飞行编队进 行 仿 真 。 邻 接 矩 阵 设 置 为A=[0,1,0,1；1,0,1,1；0,1,0,1；1,1,1,0]；每架无人机的初始速度均为30 m/s。

4架无人机的初始飞行条件如表1和表2所示。

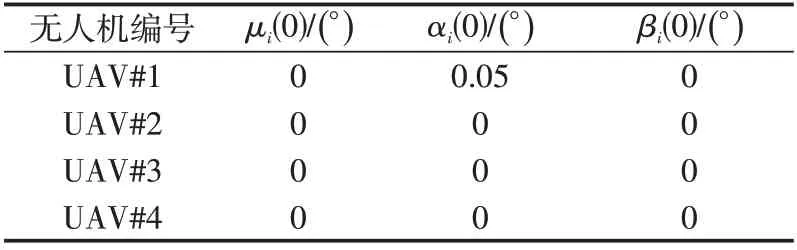
表1 无人机姿态初始参数表Tab.1 Attitude initial parameters of UAVs

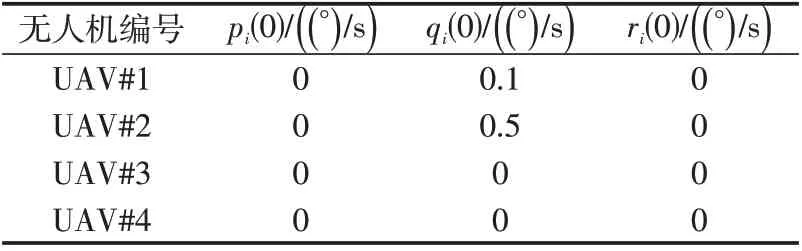
表2 无人机角速率初始参数表Tab.2 Angular rates initial parameters of UAVs

4架无人机的姿态角如图1所示。可以看出，无人机在遭遇故障的情况下依旧可以保持稳定飞行。

图1 姿态角xi1Fig.1 Attitude angles xi1

图2 展示了4 架无人机的控制输入，在遭遇故障时，控制输入能够及时做出反应。

图2 控制输入信号uiFig.2 Control input signals ui

由图3 可知，各无人机之间的姿态协同跟踪误差时刻处于预设性能界限内。

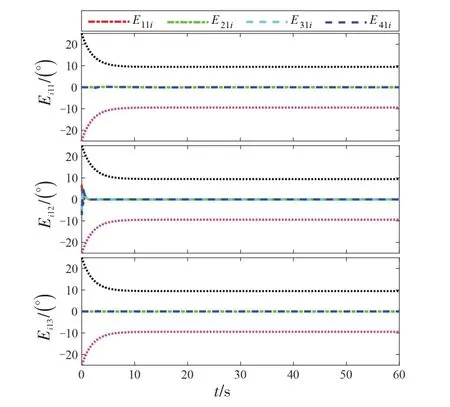
图3 姿态协同跟踪误差Fig.3 Synchronized attitude tracking errors

由图4 可见，无人机自身角速率误差均被限制在预设性能边界内，体现了预设性能容错控制的有效性。

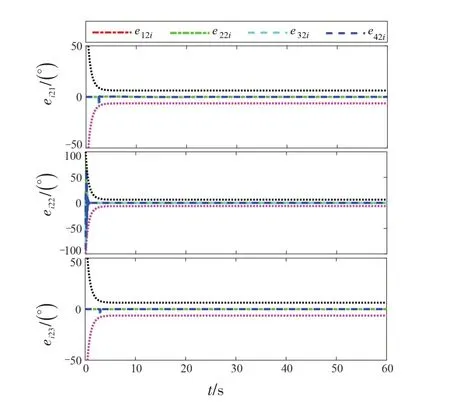
图4 无人机自身角速率跟踪误差Fig.4 UAV's own angular rate tracking errors

通过以上仿真结果可知，在无人机遭遇增益故障时，本文提出的基于Nussbaum-type 函数的预设性能反步容错协同控制方案，展示了较强的容错效果与较好的跟踪性能，各无人机的姿态角几乎保持一致，同时，也保证了多架无人机在执行任务时的飞行安全。

4 结论

本文研究了多机协同执行任务过程中遭遇执行器故障情况下的容错控制问题。针对遭遇执行器故障多机协同控制系统，提出了1种基于Nussbaum-type函数的分布式预设性能反步容错姿态协同控制方法。首先，给出了固定翼无人机动力学模型，进一步将动力学模型转化为面向控制的二阶系统，并将故障模型融入系统，构建具有执行器故障的控制系统；其次，针对定义的同步姿态跟踪误差与角速率误差，引入预设性能函数，将不等式约束转化为等式约束，构造了新的误差，基于转化误差设计反步控制器；再次，采用Nussbaum-type函数解决执行器故障导致的控制律增益未知问题；最后，通过仿真验证了控制方法的有效性。