因果语法的由来与可能
2024-01-09谭浩
谭 浩
(湘潭大学碧泉书院哲学与历史文化学院,湖南 湘潭 411105)
一、普遍语法与句法范畴的思想介绍
语言学研究的一个目标就是寻找普遍语法。语法grammar 的词源追溯到希腊语中grammatika,由gramma即“字母”和tika组成,意思是“字母的艺术”。语言学中语法的意思就是语言的技艺,语法学将这种技艺从语言中抽象出来,代表了主体的语言能力,包含了语言的声音、意义、形式、词汇这四个部分,分别构成了语音、语义、语形和词典。由于存在不同的语言,语言学家对它们的抽象就意味着有不同的语法。然而杜马塞(Du Marsais)在1750年提出:“在语法中,有一些部分属于所有语言;这些部分来自所谓的一般语法(general grammar)。除了这些一般部分之外,还有那些只属于一种特定语言的部分,它们构成了每种语言的特定语法。”[1]约1630年,阿尔斯泰德(Johann Heinrich Alsted)就指出一般语法是任何特定语法的模式规范。这种一般语法是所有语言所遵循的定律(law),即表示所有语言的共性——普遍语法(universal grammar)。根据乔姆斯基的观点,普遍语法是人类天生语言能力的一部分,刻画了可能的特定语法类。语言学家寻找普遍语法正如科学家寻找普遍科学定律,是一个无限接近真理的过程。语言学家对语言习得也感兴趣。儿童显然是出色的语言学习者,他们被置身于语言环境中,无需语言指导便可学习到语言的用法而与人交流,甚至在长大以后,他们可以使用高级的语法。乔姆斯基认为,正是天生根植于人类大脑中的普遍语法能力,使得人类是杰出的学习者,他们根据现实世界的语言,以及普遍语法所产生的特定语法类,归纳学习获得实际语言能力。
语法就是描述语言能力的一个真模型,就语形中的句法理论来说,句法范畴思想已经渗透到语言学研究的各个方面。句法理论研究句子的形成规则,范畴则是从各种真实语句中总结抽象出来规则所运用的组成部分。句法抽象的是语义之外的仅表示语句的共有结构,而范畴就是结构的端点。下面就以基本范畴语法(Basic Categorial Grammar,简称BCG)举例介绍。[2]BCG的范畴集由基本范畴集和其上的连接词“/”和“”构成的复合范畴组成。
定义1(范畴)
B为基本范畴集,CAT(B)为范畴集,是满足下列条件的最小集:1.B为CAT(B)的子集;2.如果A,B为CAT(B)的元素,则(A/B)为CAT(B)的元素,(AB)为CAT(B)的元素(一般约定最外层括号是省略的)。
在语言学中,基本范畴集一般可能由不同的元素组成,比如B={s,n,vp,v}或者B={s,np}。其中,就和语言的词性对应来说,s代表句子,n代表名词,np代表名词短语,v代表动词,vp代表动词短语。其中比较特殊的是范畴s,因为范畴之间的结构形成句子,那么就意味着范畴的形成要体现词汇(词汇类,范畴)与句子之间的关系,所以s一般而言是不可或缺的。既然范畴对应词性,归根结底它表示的是实际语言的具体词汇类。BCG通过词典来规定词汇与范畴之间的关系。
定义2(词典)
已知非空字符串集∑+和基本范畴集B。BCG词典LEX为∑+和CAT(B)的有穷关系。
具体来看,词典就是将每个词汇指派一个范畴,然而某些词汇可能有不同的词性,所以可能会指派给不同的范畴。给定了词典和范畴,接下来要确定范畴如何组成句子,即需要一个形成句子的规则。BCG的规则所使用的是矢列演绎系统。一个矢列公式就是如A1,...,An⇒B的形式,其中A1,...,An称之为前件,⇒称之为演绎,B称之为后件。该演绎系统由以下公理模式和Cut规则组成:
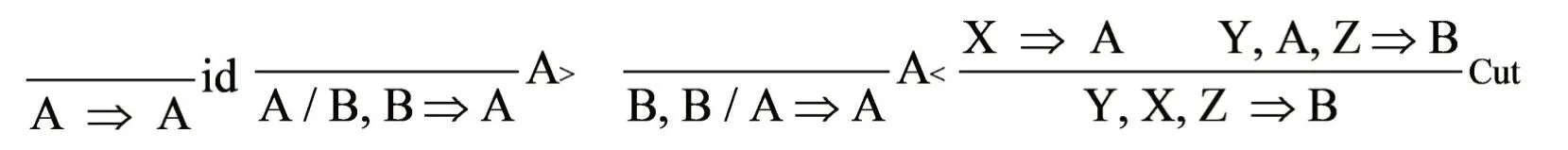
其中横线之下的矢列称之为从公理id、A>、A<与Cut规则有限多次运用由横线其上的矢列可导出,显然横线之上没有矢列则意味着无条件可导出。将此矢列演绎系统运用于范畴之上可得:
定义3(可导性)
已知B为基本范畴集,┝B称之为由B(确定的范畴集)可导关系,X⇒A由B可导即X⇒A属于┝B写作┝X⇒A。该可导关系集是满足下面条件的最小集合:对于任意的A,B,C属于CAT(B)以及X,Y,Z属于CAT(B)构成的有穷序列,有1.┝A⇒A;2.┝A/B,B⇒A;3.┝B,BA⇒A;4.如果┝X⇒A而且┝Y,A,Z⇒B,那么┝Y,X,Z⇒B。
就BCG而言,既然它要确定生成一个句子,那么可以指定一个集合S为最终要得到范畴集,一般可取S={s},其中s就是指表示为句子的范畴。这样,BCG句法由如下定义:
定义4(BCG句法)
已知非空字符串集∑+。BCG句法G为三元组
下面通过一个例子[3]310来说明BCG的句法生成。
令B={s,np};
LEX={
S={s};
有了如上确定的G,可以生成L(G)={catseatfish,fisheatcats},可以看到G生成的语句是没有空格字符的,但是并不影响理解。其中catseatfish的生成可由下面矢列形式分析树表示:
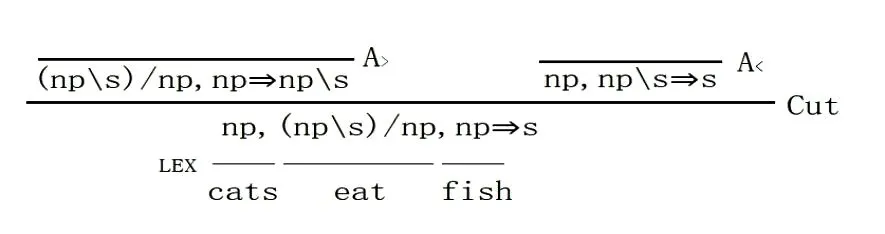
图1 catseatfish的BCG矢列分析树
将矢列形式的前件写在横线之上,演绎符号写为横线,后件写在横线之下,适当地将相同的后件与前件进行合并,该矢列形式分析树可写为更易看出生成结构的如下分析树:
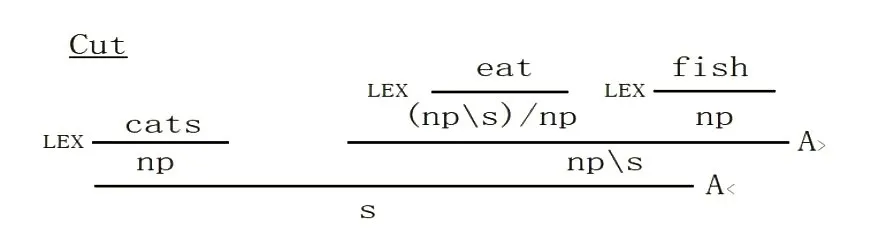
图2 catseatfish的BCG结构分析树
可见该句结构如下图:
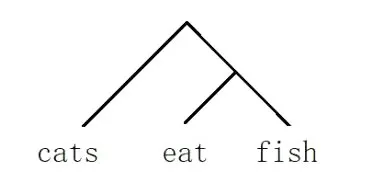
图3 catseatfish的二叉结构
显然,该语法下也可以生成同样结构的fisheatcats。保持词典不变,通过更改BCG所运用的演绎规则,可以生成同样结构的catsfisheat,这种SOV(主语-宾语-谓语)形式的句子一般出现在日语之中,不同于之前的SVO形式。特殊的情况下,如果句子的结构图如下:
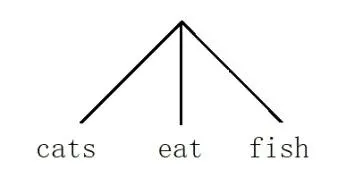
图4 catseatfish的三叉结构
则会称该句子的生成没有遵循一致的语法,或者至少没有遵循与BCG一致的语法。前面的几种情况与BCG一致,因为它们生成的结构相同,虽然可能属于不同的语法。这样就可以区分四类情况,一是BCG确定的一致结构的SVO形式,二是BCG确定的一致结构的SVO形式另一个具体实例,三是与BCG一致结构的SOV形式,四是与BCG不一致结构的形式。可以看到,语法分析具有三个层次,一是语法层次,二是分析树(结构),三是具体形式。前面一二情况具有同样的语法,结构,但是具体形式不同;三具有不同的语法,但结构一致,具体形式不同;情况四则结构不一致。这四种情况的最大公约数就是结构一致性问题,为了体现语法对结构的指导,与BCG一致结构的语法就成为了目前第一层次的存在。根据普遍语法思想,它生成所有具体语法,就意味着成为最高层次的存在。
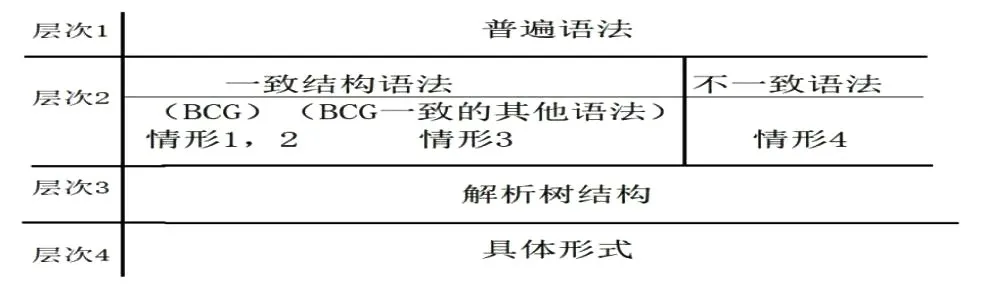
表1 语法分析的四种层次
二、普遍语法思想对因果理论的启示——因果语法
语言习得是归纳推理的过程,可以根据这种层级来规定。从原则上讲,任何一种真实语言的语法可以推出数量与复杂度上无限的结构集,并且推出无限具体实例。因此每个更高抽象层次都会生成下级情形,从而限制了更低层次的可能假设空间。因此语言的学习就变成了,结合该层次生成的较低级别的观察数据与该层次的较高级别生成的可能假设空间,推断在中间的抽象级别的层次内容。比如运用已知的语法推断具体语句的结构。然而,普遍语法的表示形式尚无共识,但是层次2的理论规定了一组抽象类别(范畴)和规则(演绎),这种构成也许是普遍语法可以借鉴的形式。这种形式可以只从下层实例归纳获得,比如通过具体语句总结结构;也允许在同一层次内部的推理,比如在语句缺词的情况下根据规则进行补完。因此,在每个层次都存在三种类型的学习与推理,一是同层次推断补完,二是从下层实例归纳学习获得该层知识,三是在上层知识约束的假设空间内,通过下层实例归纳学习获得该层知识。
因果图模型(网络)在一定程度上对应于具体语句的分析结构。进一步的类比可以得到最低级别的事件层次,即因果图中变量取特定值的实例。上一层级的因果理论层级,正如特定语言中的结构解析树是由更抽象的知识级别(一致语法)生成的,可以生成特定因果网络的假设空间。这种高一级别的因果理论可以称之为因果语法。与普遍语法类似,因果语法可能取决于一个真正的(和天生的)基础,即通用理论。因此,从高到低这四个层级分别是,通用理论,因果语法,因果图,事件。正如语言语法理论通常根据抽象句法范畴和语句构成规则来构建理论一样,我们也可以根据抽象因果范畴和范畴间的因果规则(也可称之为因果律)对因果语法进行形式化。由于因果图模型已经存在因果贝叶斯网络的表示形式,所以因果语法、通用理论也可以考虑通过贝叶斯网络进行形式化。
同样,在因果学习和推理上也存在三类问题。一是同层次的原因推断和预测结果。这是一个因果网络的补全过程,通过因果贝叶斯网络在因果图层次是可以做到的。它推断相关事件中隐藏的原因,或预测其未观察到的结果,将系统中因果联系起来形成完整网络结构。二是学习因果关系网络。在因果语法知识提供的约束候选因果结构中,根据下一层级的事件实例,在中间层次推论因果关系网络。三是学习因果语法。在未知通用理论的情况下,通过下层知识归纳学习上层知识。显然,如果只是从数据中学习因果网络结构的统计方法,在机器学习还是心理学等方面,作为拟合或构建因果模型的最基本的自下而上过程,都需要大量的训练实例。正如杰出的语言学习者儿童一样,因果网络的学习者通常也只是观察到稀疏的事件数据。例如,舒尔茨(Thomas Shultz)区分了因果关系的统计观点和因果机制观点,统计观点由因果之间因果共变特征确定,因果机制主要被定义为“力和能量的生成传递”。他的实验表明,学龄前儿童优先考虑能量传递的空间因果过程的证据(或线索),而非共变证据。对于共变证据,成年人更善于使用,但是也在直觉上更喜欢生成传递证据。[4]因果语法方法下,因果学习将自上而下和自下而上的约束整合在一起,以在与学习者理解相一致的候选中寻找最佳因果模型。这种观点似乎解释了人们如何从如此少的数据成功推断因果结构。实际上,除了高一层级的知识可约束因果模型的空间,其他的同层级先验知识也有可能。最终学习到的知识都要根据对所观察到的原始数据的解释程度来间接评估。下面通过简单的说明来举例因果语法的知识。[3]305
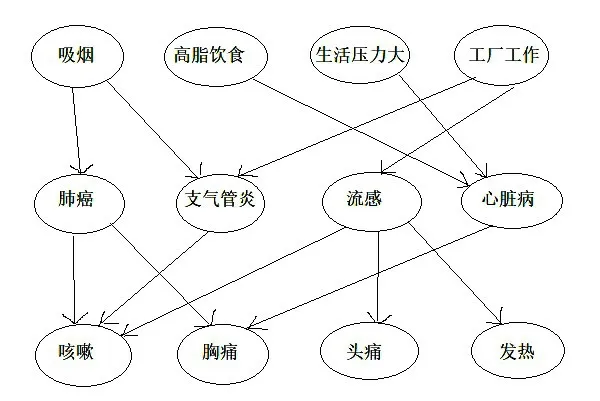
图5 症状和危险行为的因果知识网
该图代表的是几种疾病,其结果(症状)和原因(危险行为)的知识网,箭头代表可能的因果关系。给定一个患病个体的一个或多个观察到的症状,该网络给出了一组因果解释。网络还为假设分配相对概率。如果也观察到患者的某些行为,那么隐藏疾病变量的那些概率将发生变化,以反映从观察到的行为到症状的最可能途径。[3]304这种网络当然需要一种因果语法知识来进行构建,以表征该图与下面三个图之间的共同特性。
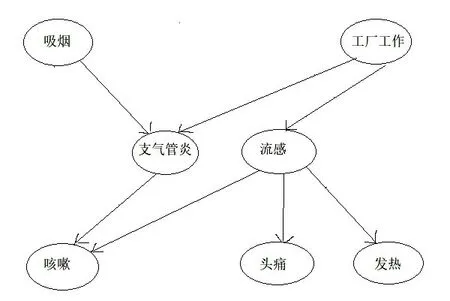
图6 具有共同因果语法特征的因果知识网(a)

图7 具有共同因果语法特征的因果知识网(b)
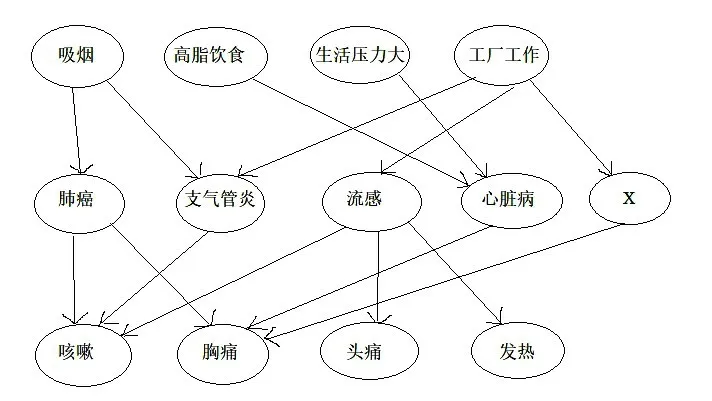
图8 具有共同因果语法特征的因果知识网(c)
该共同特性,又即因果语法可以用两个原则来简单说明:一是存在三类变量,症状,疾病和行为。这些范畴是开放的,并且大小不确定,因此可能会引入新变量。二是变量之间的因果关系因这些范畴而受到限制,可能的直接原因仅出现在从行为到疾病,从疾病到症状之间。显然前者规定了因果语法的范畴,后者规定了规则。下面两个图则提供了与该语法不一致的实例。
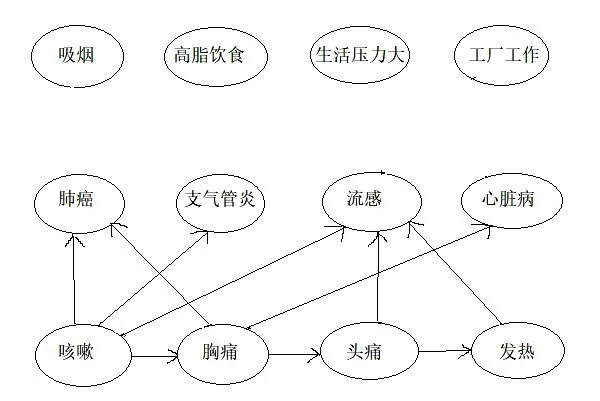
图9 不一致因果语法特征的因果知识网(a)
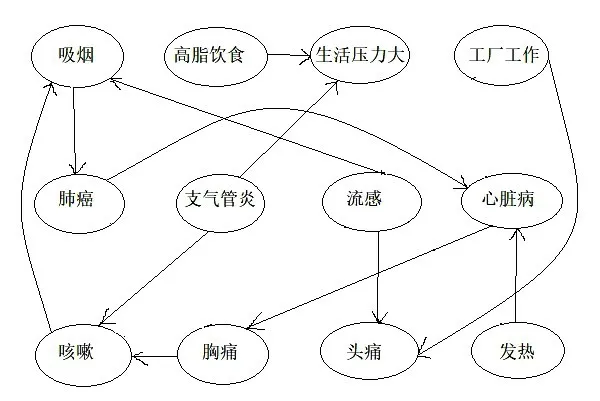
图10 不一致因果语法特征的因果知识网(b)
但上述语法表示是非形式化的,为了形式化表示就需要形式化语言。在贝叶斯方法的基础上,除了基于概率图模型的表示,还有基于多体谓词逻辑的表示方法。这两种方法存在表达能力和可学习性方面的权衡(trade-off),显然逻辑方法由于直接涉及到因果节点的语义层面,表达能力更强,但是复杂性更高。而且在逻辑上并没有一个统一的学习框架,因此对它的论述借助于小规模实例是有益的。
三、多体谓词逻辑表示的因果语法①
为了定义统一的逻辑术语,我们便有如下规定。常量用小写字母或单词(或加下标)表示,变量用大写字母(或加下标)表示,谓词用首字母大写单词(组)(或加下标)表示,全称量词用∀表示。需要注意的是,如果论域中有三个实体p1、p2和p3,则式∀P ChestPain(P)表示三个实体都具有胸痛属性,它所涉及的是命题的真相,亦即该式被写出就当且仅当该式的真值为真(真是冗余的陈述)。多体逻辑将实体划分为各种类型,并对谓词可以应用的实体类型加以约束。我们使用与谓词相同的表示法来引用类型,因为类型自然会转换为谓词。[5]334比如对于疾病,我们可能要区分两种类型的实体——People 和Object,并断言ChestPain是仅可应用于People类型的实体的谓词。由于类型的引入,这种多体谓词逻辑更加提供了比图语言更丰富本体的表示方法。下面就以blicket检测器的案例用它进行形式化。
blicket是一种特殊的立方块(block),存在许多方块,其中一些是blicket,它们与其他方块几乎无区别,而且blicket 只能通过blicket 检测器检测出来。受试者被告知通过将一个或多个方块放在检测器上,通过一些列试验,被要求说出哪些方块具有使检测器激活的能力(表示检测到了blicket)。戈普尼克(Gopnik)和索贝尔(Sobel)在其实验中,孩子们在一系列试验中看到一起放置在探测器上的两个块a和b,或者分别放置在探测器上。在每次试验中,blicket检测器被激活或者没有动静。这样的实验结果肯定和每次试验的顺序有关。用变量A和B对块与检测器之间的接触进行编码,用变量E对检测器的响应进行编码。接下来,对该实验所涉及因果语法进行形式化如下。
该理论包括本体,因果结构的表示。作为因果网络的生成语法,该理论分别生成网络的节点,节点之间的因果关系。本体规定了论域中实体的类型并在这些类型上定义谓词。这些类型是按层次结构组织的,首先分为Object,Power 和Trial。Object 类型进一步分为Block 和Machine。谓词分为结构谓词和因果谓词。因果谓词指定的变量在因果网络中显示为节点。结构谓词指定论域中实体的基本属性,并约束了基于因果谓词所定义的候选因果网络。这样,有两种类型的因果谓词:如果在试验T上对象O和O'接触,则有Contact(O,O',T);如果机器M在试验T上处于激活状态,则有Active(M,T)。这些谓词均适用于特定的Trial,代表实验的离散时间间隔。有两个结构谓词:如果对象O 拥有力P(比如是blicket),则有Has(P,O);如果力P 激活机器M,则Activates(P,M)(如该机器是blicket 检测器)。需要注意的是,这里假定只有一个力概念,即bilcket,是一种理论实体或属性。理论的因果律指定变量之间必须或可能存在的因果关系。该理论的结构性规定决定了特定因果关系存在的可能性。每个规则都包含一组根据结构谓词陈述的条件。该因果语法可由下表示。
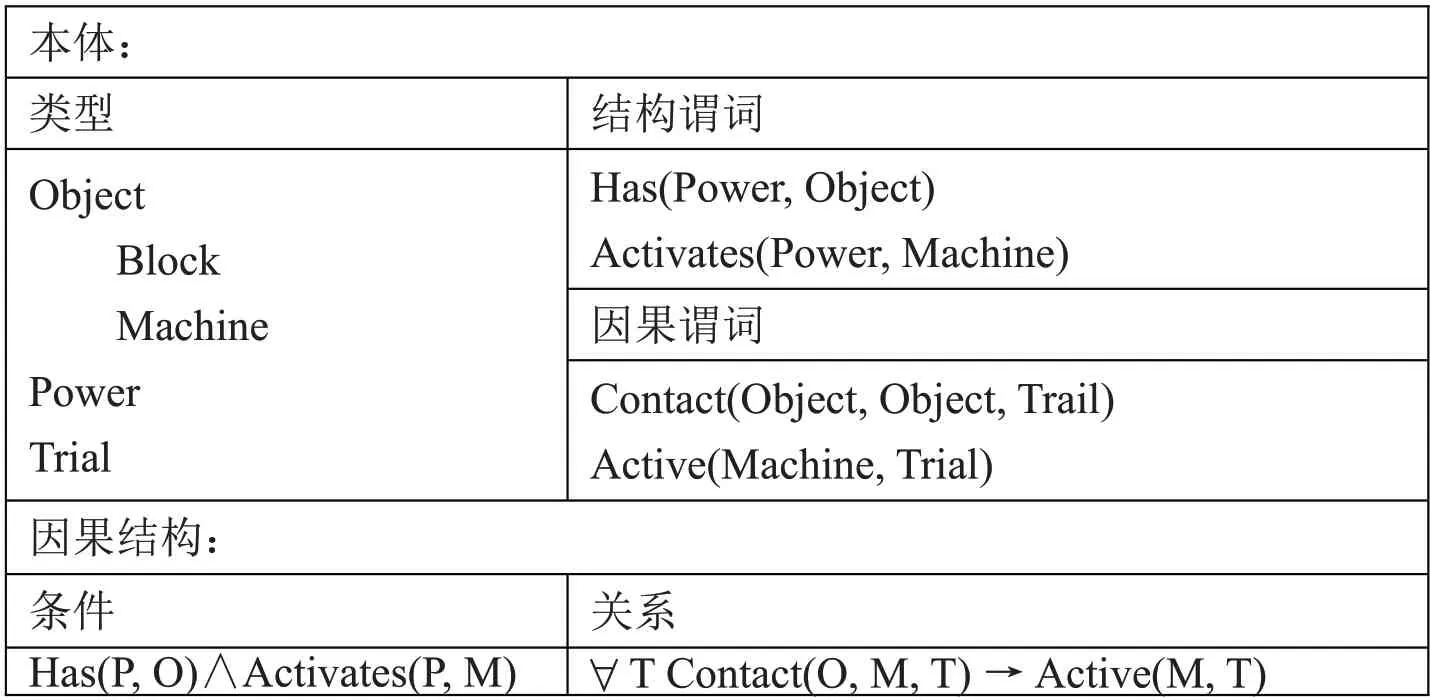
表2 blicket检测器的多体逻辑因果语法
该因果语法可以生成因果网络的假设空间。假设我们有两个块a和b,一个检测器d,一个力blicket,并且知道d由该力激活,则谓词集如下:Contact(a,d,T),Contact(b,d,T)和Active(d,T)。因为因果关系在所有试验T中都是恒定的,所以我们可以用四个图结构来表示这些可能因果网络。其中,我们使用变量A和B分别表示Contact(a,d,T)和Contact(b,d,T),而E表示Active(d,T)。
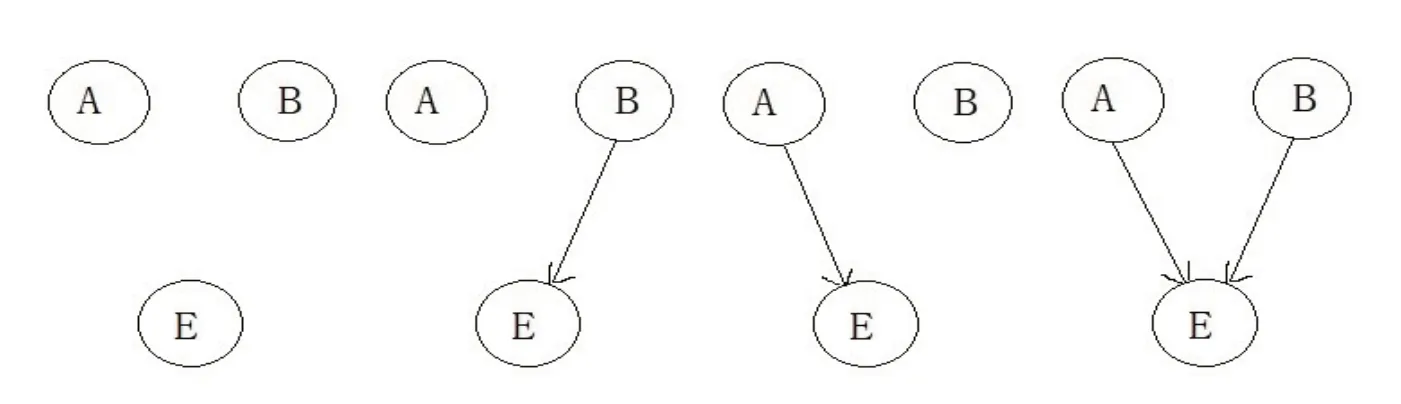
图11 blicket检测器的因果网络假设空间
在blicket实验中,通常要求学习者判断一个块(例如a)是否是一个blicket。此问题询问Has(blicket,a)是否为真。因为Has(blicket,a)在逻辑上条件于Contact(a,d,T)和Active(d,T)之间存在因果关系,所以可以将这个问题简化为关于因果网络结构的贝叶斯推断。blicket实验的因果学习过程由许多科学家进行了分门别类的研究。比如,特南鲍姆(Tenenbaum)等研究了反向阻塞(backward blocking)条件的实验。[5]339-341卡明(Kamin)将“阻塞”一词以说明在多因实验中,其中一个因与结果配对,它能获得正的关联强度,同时在加入另一个时,就并不能获得与结果的关联,因为它被已学习到的因果关联所阻塞。[6]反向阻塞则,受试者首先暴露于复合刺激下,然后才暴露于单独刺激,会产生对其中之一的关联强度的下降。该实验在成年人身上进行。受试者者被随机分为两组,不同的是他们如何引入先验概念。最初为两组受试者展示12个方块,一次放置在检测器上。在罕见(rare)情况下,这些方块中只有2个导致探测器启动。在常见(common)情况下,检测器会激活12个中的10个。这样可以假设学习者的先验概率为,在罕见条件下为1/6,在常见条件下为5/6。实验的判断阶段分为三次试验,在第1阶段中,仅向受试者展示了2个新方块,a和b;在阶段2中,受试者看到a和b一起放在检测器上,并激活了检测器;在阶段3中,仅将a放置在检测器上,并激活了检测器。在每个阶段之后,要求受试者对a和b是blicket的概率进行评分。通过对实验结果的权变(contingency)计算和利用贝叶斯模型计算结果的比较,得到该模型确实具有符合实验的学习性。在罕见情况下,在阶段2后,a和b成为blicket的概率增加;然后,阶段3试验提供了明确的证据,即a是blicket,而b是blicket的概率返回到阶段1时先验概率的情况。而在常见情况下,在阶段2后,a和b成为blicket 的概率没有明显变化,阶段3使a是blicket 的概率为1,而b是blicket的概率稍微下降。这些结果如下图引自注释1,其中横坐标从左到右表示三个阶段。至于高层次知识的学习问题可参见该注释的论文。
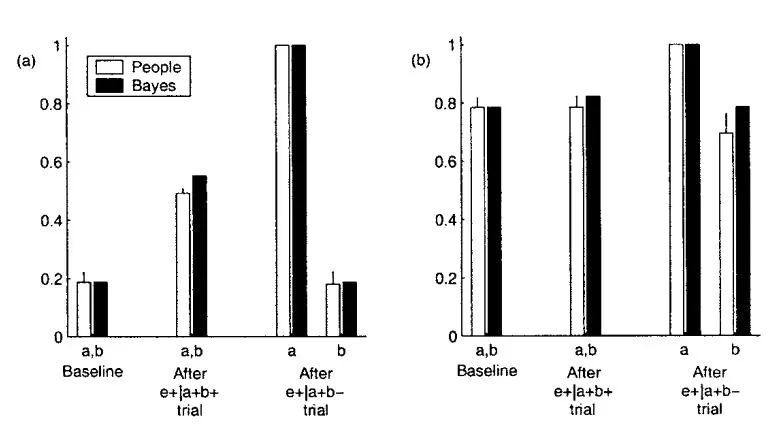
图12 blicket检测器的反向阻塞实验结果
需要注意的是,以上只是因果语法可能是什么样的建议,而不是充分的说明。这仅是一些理论的可能模型,这些模型可以解释人们因果推理能力的特定方面,并非一般的普遍的形式化模型。人们对因果语法的确切描述可能难以捉摸,就像对自然语言语法一样。从人们对语言的陈述或因果关系的判断的观察数据,到人们在做出这些判断时所承担的不可观察的抽象知识的形式描述,这种向后归纳工作并不容易。[5]343但这种因果语法的思想,为定位自然语言中因果语义的研究提供了工具。
四、从因果语法回到因果语义
首先需要说明的是,之前因果语法的术语所表示的是因果理论范畴,而这里因果语义的术语所表示的是语言学中的,语言所揭示出的是因果关系的语义关系。其基本思想是,因果分析是语言分析的基础,语言分析影响因果分析。[7]伦纳德·泰尔米(Leonard Talmy)关注于语言中的表示因果关系的语义分析。其中因果致使关系是基础的概念,致使是语言中的范畴,是人们对现实世界因果关系的认知结果。[9]泰米尔区分了多种复杂程度各异的因果致使(causative)情境,并将它们解析为基本的语义元素以及它们的组合。[8]其中,最为基本的语义情境称之为自主事件(autonomous events),最基本的致使情境称之为基本致使情境或基本因果(basic causation)。复杂因果是由自主事件,其他类型事件,基本因果,复杂因果组合而成。
语义分析中的致使术语表示的也是事件间的因果关系,这与因果理论是一致的。不同点便在于自主事件可以被认为是事件的潜在自我致使。比如“Water poured from the tank.”这个句子的事件被表述之后若要寻找其原因,也必须要付诸外部事件对其的致使,但是在语义分析中,该句的致使性并不能逃出该句本身,因此称之为自主事件。自主事件可以作为一个完成致使情境、因果情境、基本因果的组成元素。基本致使情境除了作为组成部分,也是所有复杂致使情境的共有结构。它由两个简单事件与它们之间的因果致使关系组成,由句法表示如下。②
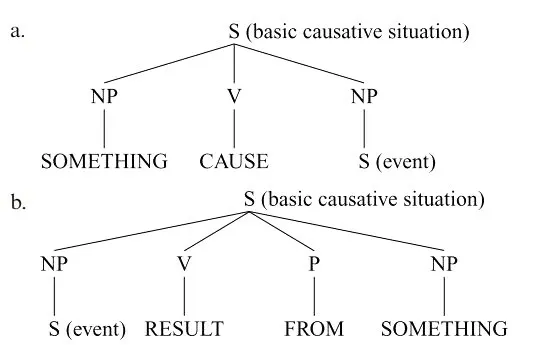
图13 基本因果致使结构的认知语义分析树
这个结构中的something 从某种意义上来说应指事件。比如“The window's breaking resulted from a ball.”若要表达致使义,其句式应该补全为“The window's breaking resulted from a ball's sailing into it.”。如若不清楚补全内容,可以用力这样的抽象实体以表明,如“The window's breaking resulted from a ball's power.”在这个句子中,球具有使窗户破损的力,并且施展了出来,成为一个事件。因此,上面a.和b.的语言形式可以视为a.S(event)CAUSE S(event)和b.S(event)RESULT FROM S(event)。这样,一个事件(cause左边的S事件)被称为致使事件,另一事件(在cause右边的S事件称为被致使事件或结果事件),对b的情况相反。
泰尔米还分析了复杂致使情境,这些情境包括:
A ball's rolling into it broke the vase.(致使事件的致使情境)
A ball broke the vase in(by)rolling into it.(工具致使情境)
I broke the vase in(with my/by)rolling a ball into it.(作者致使情境——有非预期结果)
The branch's falling down on it toppled the aerial.(2事件致使情境)
I slid the plate across the table by pushing on it with a stick.(连续致使情境)
具体可参见注释2。那么因果语法如何回到因果语义?这是一个开放的问题。首先,各表示致使关系语句的具体形式处在最低层级,它表示了一类(复杂)致使关系。然后,致使关系结构当属上一层次,但不同的复杂致使关系所表达的是简单事件的复合,该种复合关系如果是因果关系,那么就可以通过因果理论来表示成为因果网络,如果不仅是因果关系,则需要结合其他理论共同表示。最后,具体致使网络的高一级别理论产生了该层网络的候选假设,即意味着基本致使关系模式S(event)CAUSE S(event)处在该层级。这样,从现实中的不同因果关系,都可以产生无数的致使语句,而对致使语句的语义分析,最终可以通过建立高层级的现实因果理论来获得。而致使语句的因果结构,也不仅可以从具体语句中归纳获得,也可以从高低两个层级知识归纳获得。这便是从因果语法获得的对因果语义分析的启示。
注释:
①该节例子引自Joshua B.Tenenbaum,Thomas L.Griffiths.Two Proposals for Causal Grammars[A]//A.Gopnik,L.Schulz.Causal Learning:Psychology,Philosophy,and Computation[M].Oxford,UK:Oxford University Press,2007:333-342。
②图引自Talmy L.Toward a Cognitive Semantics,Vol.1:Concept Structuring Systems.Language,Speech,and Communication[M].A Bradford Book:The MIT press,2000:481。
