基于表面外推法的结构热点应力计算方法研究
2024-01-09赵春雨柳胜举黄文杰秦瑞冰
许 波,赵春雨,柳胜举,黄文杰,秦瑞冰
(明阳智慧能源集团股份有限公司,广东中山 528400)
0 引言
“十四五”规划要求大力发展新能源等新兴产业,风电行业迎来高速发展,风电机组也朝着大兆瓦发展,机组重量显著增大,对风电机组安全性、稳定性要求也越来越高[1-3]。风电机组部件有很多为焊接件,这些部件承受比较复杂的动静载荷,并且其焊接接头受焊接缺陷、应力集中的影响,疲劳强度大大降低[4-6]。由于应力奇异的影响,直接提取有限元直接计算结果不准确,且与通过结构热点应力法计算出的安全系数相差较大[7]。因此,国内外研究人员通常借助结构热点应力法计算关键位置的热点应力,进而评定焊接接头的疲劳寿命。因此,准确计算出热点应力,对风电机组焊接部件寿命设计具有重要意义。
结构热点应力法计算相对容易、效率高,被IIW(国际焊接学会)、DNV(挪威船级社)等协会纳入相应的疲劳寿命设计规范,用于计算热点应力[8-11]。吉伯海等[12]对钢桥面板顶板与U肋焊接接头的疲劳分析中发现,线性外推法与二次外推法计算的热点应力相近,接头附近应力对网格尺寸较敏感;板壳有限元模型网格尺寸细化到1.0t时,可得到稳定的热点应力。韩冰等[13]对比了4种单元类型对热点应力计算的影响,发现高阶单元稳定性更好,板壳单元得到的热点应力值更小。韩庆华等[14]采用多种外推法计算结构热点应力,IIW 建议的外推法计算结果大于DNV 建议的外推法计算结果;三点二次外推法计算结果略大于相应两点线性外推法计算结果。傅中秋等[15]对比热点应力取值方法对结果的影响表明,两点线性外推法和三点二次外推法计算得到的热点应力几乎相同,表面外推法得到的热点应力比沿板厚积分方法和表面1 mm 应力法结果大5%~10%。揭志羽等[16]研究发现,网格尺寸对热点应力的计算结果影响较大,当网格尺寸小于0.1t时,可忽略网格尺寸的影响。柯璐等[17]计算钢箱梁焊接接头的热点应力后发现,高阶单元模型对网格尺寸的收敛性较好,且计算精度优于低阶单元。对于风电行业焊接部件的结构热点应力计算方法研究较少,因此需要结合行业设计经验,探究合理的建模、计算方法,获得较为准确的结构热点应力,进而确保部件疲劳设计寿命的可靠性。
本文根据实际载荷、边界条件,建立不同单元类型、网格尺寸的有限元模型,对比分析网格尺寸、单元类型、外推方法对焊接接头结构热点应力计算的影响规律。
1 结构热点应力计算方法
1.1 结构热点应力定义
结构热点应力σhs是焊趾缺口处的局部应力。焊趾缺口处应力分布呈现高度非线性,这种非线性应力由膜应力σmem、弯曲应力σben和非线性峰值应力σnlp组成[14]。
结构热点应力只受限于焊接构件的几何形状,包含本身结构引起的应力集中效应,不包含焊趾局部缺口效应造成的非线性峰值应力σnlp[8,18-19]。尤其是对结构复杂且不连续、难以定义名义应力的焊接接头,推荐使用结构热点应力法,结构热点应力可通过远离焊缝的2 个或3 个参考点处的应力,外推计算得到。对于非线性应力分布明显对的焊接接头,建议采用三点二次外推法计算结构热点应力[20],如图1所示。
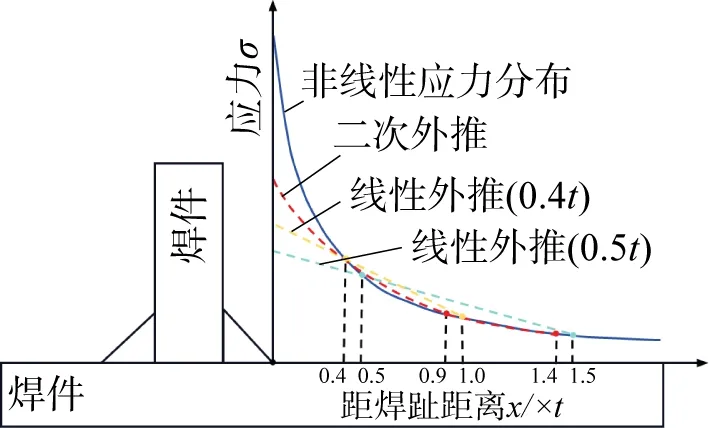
图1 外推法示意图
1.2 表面外推方法及原理
结构热点应力首先确定参考点处的应力,其次根据外推计算得到结构热点应力。离焊缝最近的参考点必须足够“远”,避免焊缝处缺口效应造成的非线性峰值应力影响,又要尽可能接近焊趾符合实际。这个距离一般为0.4t(t为焊件厚度)。利用拉格朗日插值法中的两点线性插值公式和三点二次插值公式分别列出σhs的两点线性插值法和三点二次插值法的解析式。
式中:σhs为焊趾处结构热点应力;x1、x2、x3分别为参考点与焊趾之间的距离;σ1、σ2、σ3分别为参考点处的表面应力。
IIW 规范中给出参考点与焊趾之间的距离,两点线性外推法根据网格尺寸分为两种[8]。对于细网格模型(网格尺寸不超过0.4t)选择距离焊缝0.4t,1.0t的点作为参考点。
式中:σ0.4t、σ1.0t分别为距离焊趾0.4t和1.0t处参考点处的表面应力。
对于高阶单元、粗网格模型,选择距离焊缝0.5t,1.5t的点作为参考点。
式中:σ0.5t、σ1.5t分别为距离焊趾0.5t和1.5t处参考点处的表面应力。
三点二次外推法适用于非线性应力分布明显的焊缝接头,且为细网格模型,选择距离焊趾0.4t,0.9t,1.4t的点作为参考点。
式中:σ0.4t、σ0.9t、σ1.4t分别为距离焊趾0.4t、0.9t和1.4t处参考点处的表面应力。
2 有限元计算建立
本文以风电机组工装为算例,建立工装完整的有限元模型,如图2 所示。工装内部的连接螺栓通过梁单元模拟,工装底部焊接固定,所以底部施加全约束。选取工装其中一个支腿与筋板的局部焊缝区域作为研究对象,如图3 所示。其中筋板的厚度为12 mm,宽度为66 mm;支腿的板厚为36 mm。整个工装的材料均为Q355,材料屈服强度取355 MPa。
图2 工装有限元模型
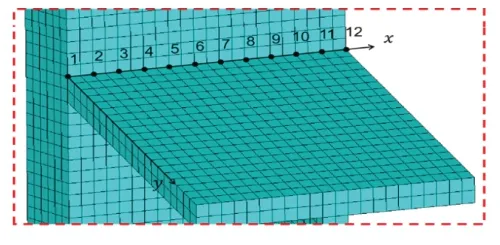
图3 局部焊缝模型
整个工装均由板件焊接而成,存在大量的焊接接头,为简化计算模型,提高计算效率,所有的焊接接头均未建模焊趾。根据IIW标准,如果焊接接头未建焊趾,为了避免焊趾刚度缺失造成应力的低估,可选择焊件交汇处作为热点。为了研究网格精度、单元类型以及外推方法对结构热点应力计算的影响,局部焊缝区域分别选择常用的六面体单元(SOLID186,高阶20节点实体单元)和四面体单元(SOLID187,高阶10节点实体单元)进行网格划分,计算五种网格精度(单元尺寸分别为0.5t,0.4t,0.33t,0.25t,0.2t,t为焊件板厚)的结构热点应力。建模完成后,首先施加螺栓预紧力完成预紧工况的计算,然后在此结果基础上重启动计算外载工况,最终得到各个模型的有限元计算结果。
3 结果分析
3.1 焊缝有限元应力计算分析
计算完成后,分别提取整理六面体单元、不同网格尺寸下的模型x向(沿焊缝方向)和y向(垂直焊缝方向)的表面应力,如图4所示。
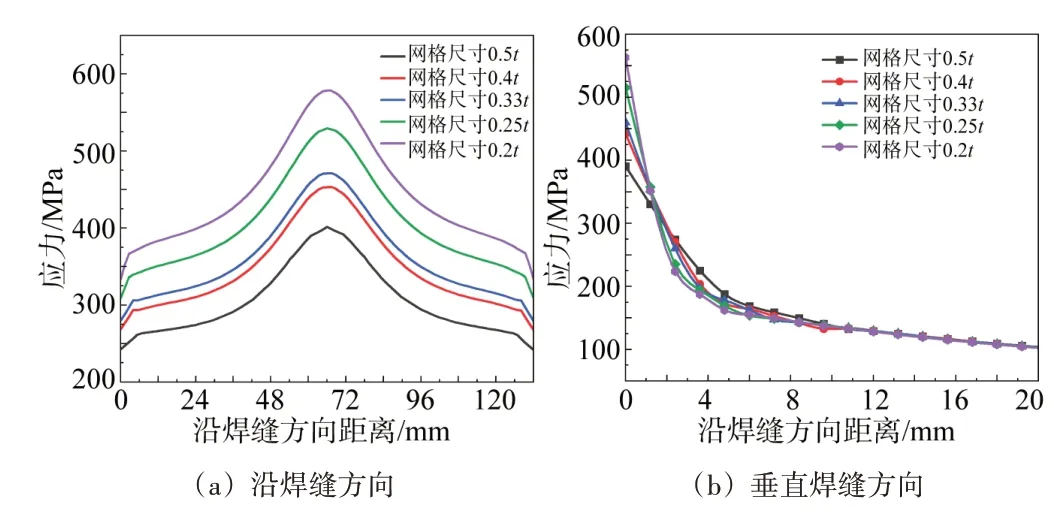
图4 焊缝区域表面应力
从图4(a)中可以看出,焊接接头的表面应力远远超过筋板的屈服强度。并且随着网格尺寸的不断细化,沿焊缝方向的表面应力逐渐增大,越靠近焊缝中心位置的高应力区,表面应力增幅越大。从图4(b)中可以看出,受非线性应力峰值影响,垂直焊缝方向的应力呈明显的非线性分布,网格尺寸越小,非线性现象越显著,无收敛趋势,因此需要借助结构热点应力法消除非线性峰值应力的影响。距离焊缝0.4t范围内,表面应力随着网格细化先增大后减小;距离焊缝0.4t~1t范围内,表面应力的差异逐渐减小,应力逐渐收敛;距离焊缝1t以外的区域,应力曲线基本重合且呈线性分布,可认为非线性应力峰值不影响该区域应力分布。
从以上分析可看出,改变网格尺寸仅对第一个参考点的应力造成影响,从而使得外推计算出的热点应力存在差异。
3.2 网格精度对热点应力的影响
选择两点线性外推法和三点二次外推法分别插值计算图示焊缝12个热点的结构热点应力。整理得到不同网格精度、不同网格类型以及不同外推方法的结构热点应力,如图5~6 所示。可以看出外推法计算出的结构热点应力远小于直接提取的焊缝表面应力,且小于材料屈服强度。
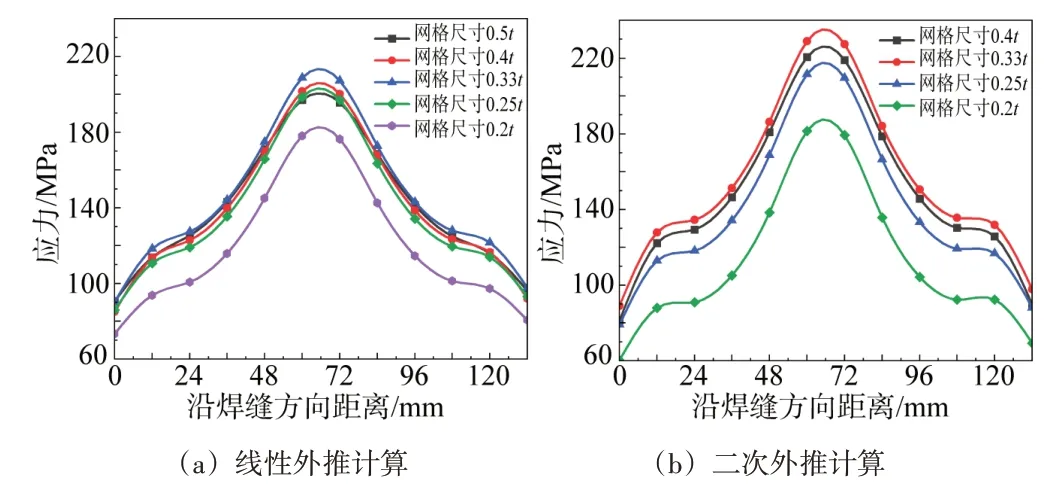
图5 六面体单元模型结构热点应力
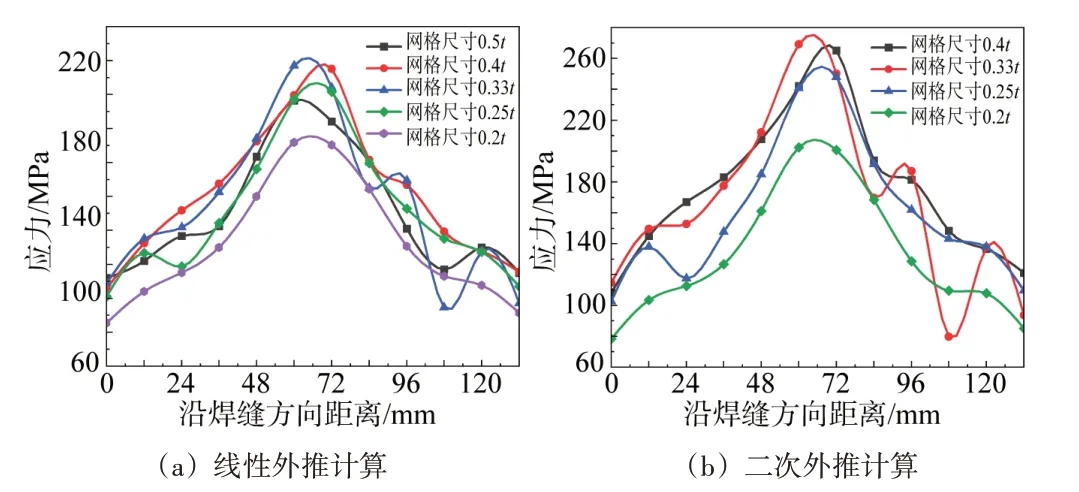
图6 四面体单元模型结构热点应力
结构热点应力随着网格尺寸细化呈先增大后减小的趋势,网格尺寸在0.33t时,计算得出的结构热点应力最大,后随着网格细化而热点应力逐渐减小。六面体单元模型线性外推法计算的最大、最小的热点应力比值为1.17,二次外推法计算的最大、最小的热点应力比值为1.27;四面体单元模型线性外推法计算的最大、最小的热点应力比值为1.23,二次外推法计算的最大、最小的热点应力比值为1.33,相比于线性外推法,二次外推法对网格精度更为敏感。
从以上分析可看出,网格精度对结构热点应力计算影响显著,从计算效率以及安全储备方面考虑,推荐局部焊缝区域的网格尺寸为0.3t~0.4t。
3.3 单元类型对结构热点应力的影响
计算整理焊缝热点6的外推结果,分析不同单元类型对结构热点应力计算的影响。从图5~6可以看出,各网格精度下,六面体单元模型沿平行焊缝方向的热点应力曲线变化平滑;而四面体单元模型计算结果有较大的离散性,在网格尺寸小于0.25t时,热点应力曲线变化趋于平滑。
单元类型对热点应力影响如图7 所示,由图可知,两种外推法下,四面体单元模型热点应力均大于六面体单元模型热点应力,且这一现象在二次外推法计算结果更为凸出。由单元类型造成的计算结果差异随网格细化而逐渐减小。

图7 单元类型对热点应力影响
从上述分析中可看出,四面体单元模型受网格尺寸的影响更显著,外推得到的热点应力结果更为保守。但是,四面体单元模型对网格尺寸要求较高,网格尺寸小于0.25t时,才能得到稳定的计算结果。六面体单元模型计算结果稳定性好,更适合热点应力法建。
3.4 外推方法对结构热点应力的影响
计算整理焊缝热点6的外推结果,分析各网格精度、单元类型下,不同外推方法对热点应力计算的影响。计算结果如表1 所示,不同外推法对热点应力计算影响较大,四面体模型两种外推法计算结果最大相差13.56%。相比于四面体模型,六面体单元模型受外推方法影响较小,各网格尺寸下两种外推法计算的应力差值比均在10%以内。两种外推法计算结果随网格尺寸减小逐渐接近,当网格尺寸细化到0.2t时,六面体单元模型两种外推法计算结果仅相差1.87%,而四面体单元模型在该网格尺寸下应力相差5.48%。IIW 规范中建议二次外推法用于非线性结构应力明显增加的热点[8]
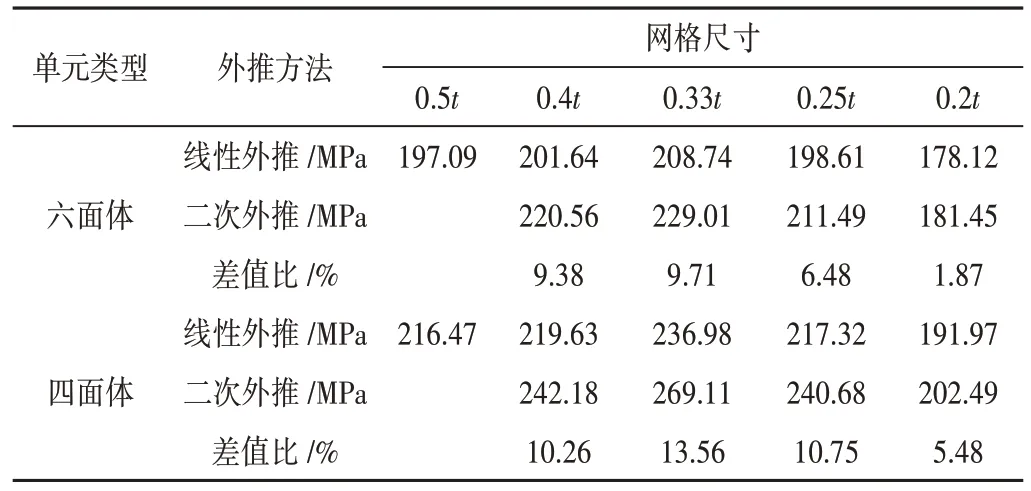
表1 不同外推方法下结构热点应力
4 结束语
本文建立风机工装有限元模型,计算不同模型的结构热点应力,得到以下结果。
(1)受非线性应力峰值影响,垂直焊缝方向的应力呈明显的非线性分布,网格尺寸越小,非线性现象越显著,且无收敛趋势;非线性应力峰值仅影响距离焊缝1t以内的区域,改变网格精度仅会影响第一个参考点的应力值。
(2)网格精度、单元类型、外推方法均对热点应力计算有较大影响;从结果稳定性、计算效率以及安全储备考虑,建议选择六面体单元建立有限元模型,局部焊缝区域按照0.3t~0.4t的网格尺寸进行划分,对于非线性结构应力明显增加的焊接接头,应选择二次外推法计算结构热点应力。
