ABAQUS退化的动力无限元单元

邹 烨

(湖南省交通科学研究院有限公司,湖南 长沙 410011)

岩土结构如隧道、高边坡、坝基等的动力稳定性一直是工程领域所关心的问题[1],而利用数值方法进行结构动力问题分析的关键之一就是边界条件的处理。岩土工程数值模拟过程中常使用人工边界条件,以实现近场区域与无限外部区域之间波动能量的交换[2],让波动自然传至无限域内。

人工边界可分为两种:全局人工边界和局部人工边界[3]。全局人工边界如边界元法,这类边界满足了无限域内的所有场方程和物理边界条件,具有较高的精度;而由于其时空耦联的特性(即某一边界节点的运动与其他所有边界节点之前各个时刻的运动有关),计算量与内存需求较大,难以满足大型工程问题的分析需求;局部人工边界是在一定的近似条件下导出的人工边界条件,目前常用的粘性边界、粘弹性边界、透射边界、无限元边界均属于局部人工边界[4]。局部人工边界具有时空解耦的特性(即边界上某一点的运动只与相邻边界节点与该节点上一时刻的运动情况有关),在牺牲一部分精度的条件下具有节省机时与内存的作用,在许多大型工程中得到了应用。

无限元是一种几何上趋于无穷的单元[5],ABAQUS中的无限元单元已有许多相关的研究与应用[6-12]。针对三维情况,仅有的八节点、十二节点与十六节点的六面体三维无限元单元要求有限域与无限域连接面为四边形,这一要求对于实际工程中复杂的地质模型比较严苛,因为复杂岩土工程模型为减小计算成本,获取更好的收敛性,往往采用四面体单元、六面体无限元单元的使用由此受到了限制。从这一问题出发,在ABAQUS中三维无限元的基础上进行改进,提出一种由六面体无限元单元演变而来的退化无限元单元以适应有限域与无限域交界面为三角形的情况,推导退化无限元单元的等效节点应力计算公式,并研究其地震动输入方式。通过建立有限元-无限元(FEM-INF)耦合分析模型进行数值试验,与理论结果进行对比验证退化无限元单元的合理性。

1 动力无限元人工边界

1.1 边界阻尼

无限元由Bettess和Zienkiewicz于1977年提出[13],用于解决有限元方法求解无限域问题时的局限性。ABAQUS中的无限元理论参考了Lysmer与Kuhlemeyer等的工作,其动力无限元可视为一种黏性吸收边界[14],通过引入边界阻尼d来消除反射。

w=f1(z-ct)+f2(z+ct)

(1)

式中:z为轴向坐标;c为波速;t为时间;w为波动所引起的边界节点位移,对于任意瞬时t,w为z的函数;f1(z-ct)、f2(z+ct)分别为入射波与反射波位移方程。阻尼力的大小可以表示为:

(2)

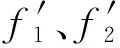
(3)

式中:G为传播介质的剪切模量;λ为拉梅常数;θ为体应变。

由边界节点的平衡条件有σ=σd,即:

(4)

(5)

(6)

同样按照‘边界上不产生反射’的要求,可得切向阻尼系数:

(7)

1.2 退化的动力无限元单元

ABAQUS提供了三种适用于连续实体介质的三维无限元单元,均为六面体单元,分别为八节点、十二节点和十八节点三种类型(见图1),单元形状决定了使用时要求有限元与无限元的交界面为四边形。对一些模型复杂的实际工程问题,网格划分时常采用适用性更强、计算规模更低的四面体单元,这时将不能使用仅提供的三维六面体无限元单元。

为解决这一问题,在现有单元的基础上提出了一种退化的无限元单元。具体做法是,让单元交界面上的任意一条边上的节点重合而退化成一个点,使交界面由(曲边)四边形退化成(曲边)三角形。交界面的退化过程见图2。

图2 交界面的退化过程

2 退化单元的等效节点力

(8)

2.1 等效节点力的计算

以地震波从底部垂直入射的情况为例,见图3。

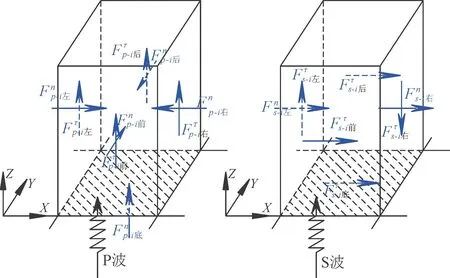
图3 等效节点力计算

(1)在P波作用下,假设输入波的速度时程为Vp(t)。

(9)

(10)

由对称性,右侧、前侧、后侧边界的法向与切向等效节点力分别为式(11)、式(12)、式(13):

(11)

(12)

(13)

(2)在S波作用下,假设输入波的速度时程为Vs(t)。

(14)

(15)

由反对称条件,右侧边界:

(16)

(17)

由对称条件,后侧边界:

(18)

各节点力的方向见图3。

上列各式中,Vp-1(t)、Vp-2(t)、Vs-1(t)、Vs-2(t)为相应节点在t时刻的振动速度,需要由入射波时程与反射波时程在计入对应的延时后叠加求得。其中:

(19)

式中:L为底面至顶面的距离,l为节点到底面的距离;当顶面非平面时,L取节点i在底面与顶面投影点之间的距离。

2.2 退化单元的等效节点力

退化单元等效节点力的计算原理与2.1节所示一样,在计算因退化而重合的节点的等效力时,把这些点仍然看成单独的点。以退化的八节点三维无限元单元为例,如图4所示。

图4 单元的转换

重合点的影响面积为:

(20)

非重合点的影响面积为:

(21)

式中:n为受节点i影响的单元的个数;Ak为单元的面积。

各边界上的等效节点力计算公式见表1。

表1 退化单元等效节点力计算公式

当节点为重合点时,q=2;当节点不是重合点时,q=4。

3 算例验证

为说明退化三维动力无限元单元的合理性,下面用数值试验加以验证。建立两个100×100×100的立方块,将这两个立方块分别划分为八节点六面体模型(C3D8)与四节点四面体模型(C3D4),以分别模拟无限域采用常规三维无限元单元与退化无限元单元的情况。立方块体模型除顶面外,其余5个面均采用无限元边界,无限元边界分别采用常规的八节点无限元单元与退化的八节点无限元单元。图5为有限元区域划分为六面体单元C3D8时的FEM-INF耦合模型;图6为有限元区域划分四面体单元C3D4时的FEM-INF耦合模型。边界上的节点一般较多,等效节点力的计算与输入要通过自编程序实现。

图5 有限域为六面体单元时的FEM-INF耦合模型

图6 有限域为四面体单元时的FEM-INF耦合模型

以P波的形式从模型底部边界垂直输入图7所示的波形,这是一个峰值加速度为4 m/s2的单峰波,其加速度为:

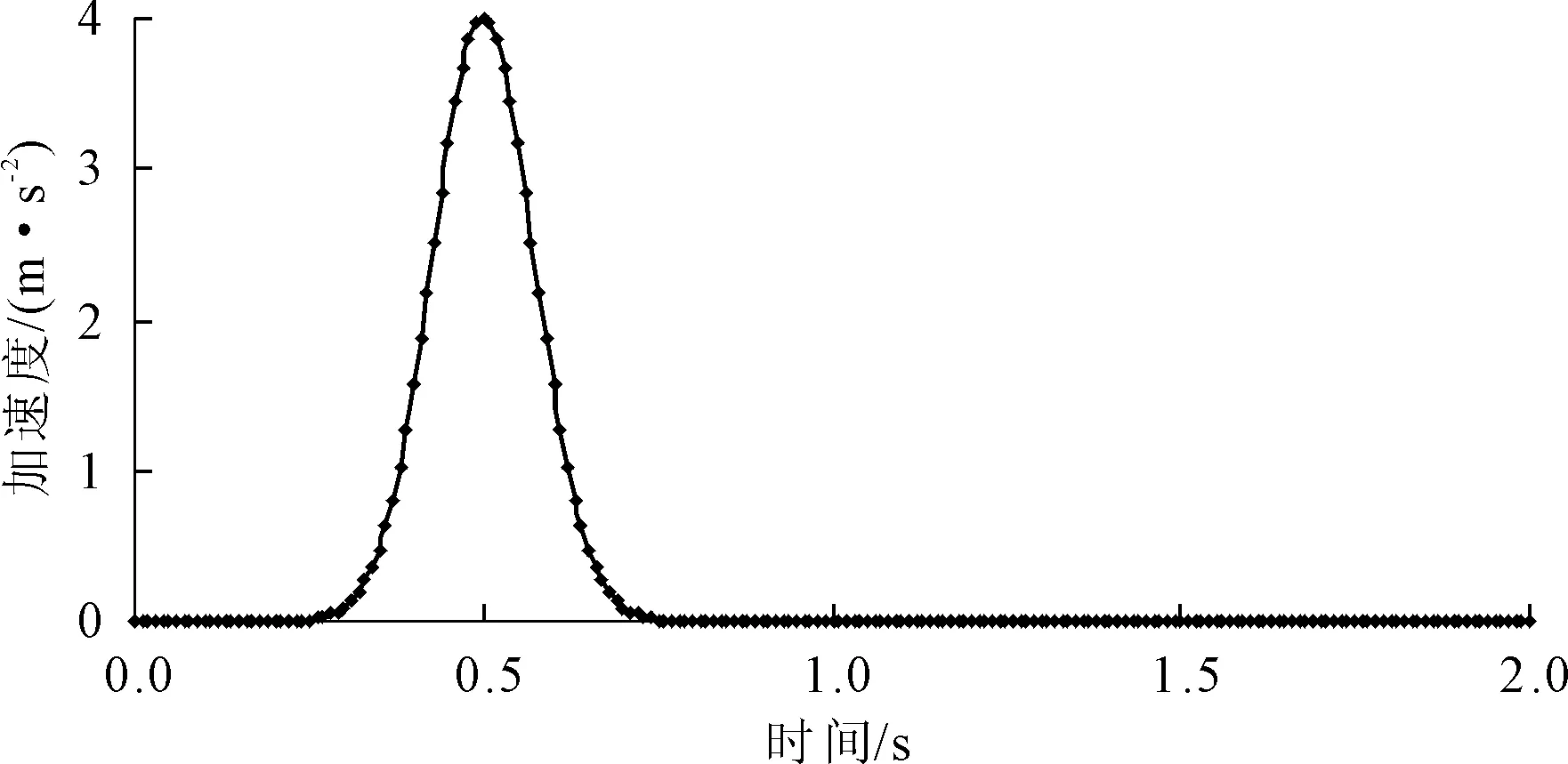
图7 入射波波形

A=4e-30π(t-0.5)2

(22)

模型的介质材料参数设置为:弹性模量E=50 MPa,泊松比ν=0.3;重度γ=25 kN/m3。模型除受重力与地震力作用外,无其他形式的力作用。

根据波速的计算公式,可得纵波波速为:cp=164.08 m/s;横波波速为:cs=87.71 m/s。因此,P波从模型底面传播至顶面的时间延迟约为0.61 s,S波从模型底面传播至顶面的时间延迟约为1.14 s。

考虑P波从底面垂直入射的情况,算例的计算结果见图8(a)。若不计立方块体材料介质的阻尼,按照理论计算的结果,P波从立方块体底部入射后,经过一定的时间延迟后到达顶面,由于这是一个与空气的界面,因此,P波将会在顶面发生反射,入射波与反射波叠加会在顶面出现一个2倍的放大效应,即顶面P波反射加速度的理论解为:

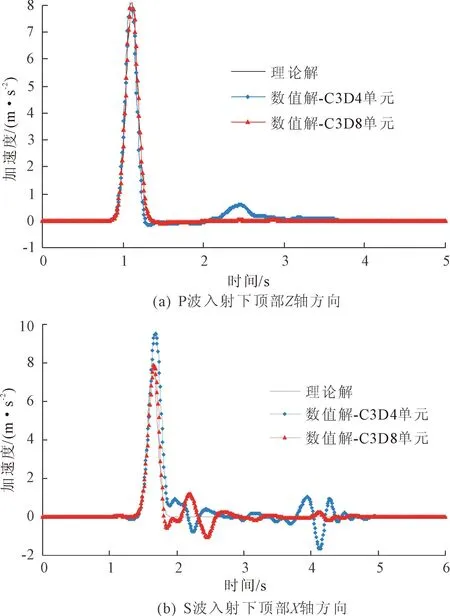
图8 加速度响应

Ap-顶=8e-30π(t-1.11)2

(23)

反射波在此传回地面后,在无限元边界的作用下,不再发生反射,传向了无穷远处,这也就是人工边界条件的作用,避免了波动多次反射现象的发生。从图8(a)可以看出,ABAQUS中的常规三维无限元单元在动力分析中取得了与理论解几乎一致的效果,而采用退化的三维无限元单元,虽在后续有小幅的波动响应,但其结果与理论解仍具有很好的吻合度。

S波从底部垂直入射的情况采用与P波入射时类似的方式进行。顶面S波反射加速度的理论解为:

As-顶=8e-30π(t-1.64)2

(24)

算例验证结果见图8(b)。从图可以看出,采用常规无限元单元与退化无限元单元对地震波均具有良好的吸收效果;采用退化无限元单元虽精度要求略低于常规无限元单元,当反射波离开顶面后,有小幅的波动现象发生,但很快趋于稳定,能基本满足动力计算上的要求。

4 结 论

在ABAQUS中无限元单元的基础上,提出了一种退化无限元单元,并利用数值试验进行验证,可以得到以下结论:

(1) 退化无限元单元能使有限域与无限域之间的交界面由四边形退化为三角形,对有限域为四面体单元的情况也能较好适用,提升了三维无限元单元对主体网格剖分方式的适应能力,且无需进行二次开发,方便工程应用。

(2) 退化单元数值模拟结果与理论解吻合良好,表明退化单元具有较好的精度,研究内容为构建复杂的FEM-INF耦合分析模型提供了便利,可应用于工程动力问题的分析。

(3) ABAQUS中采用动力无限元边界条件时,需要将地震动以等效节点力的形式进行输入。边界节点较多时,需要通过编程实现等效节点力的自动施加。

值得指出的是,研究内容虽然采用ABAQUS进行,但其中单元退化过程的处理方法对其他类似问题仍具有较好的参考意义。