高温环境下岩石热力学参数与抗压强度关系研究
2024-01-09穆智勇王新宇
杨 涛,穆智勇,杨 宇,王新宇,宿 辉
(1.河北工程大学 水利水电学院,河北 邯郸 056001;2.河北工程大学 河北省智慧水利重点实验室,河北 邯郸 056038)
在开挖水工隧洞过程中高地温现象越来越常见[1],在温度场作用下岩石内外部温差以及热力学参数不同使得同种材质的岩石有不同的力学性能,对实际工程的开展造成了一定的影响,所以研究在温度场作用下岩石热力学参数与峰值强度之间的关系是个亟待解决的问题。
杨家琦[2]利用PFC2D研究了岩石宏观力学与细观参数之间的关系,用宏观结果精确反演岩石的基本细观参数,并且利用Matlab将该算法封装成了一个程序;Potyondy[3]基于离散元程序模拟单轴压缩试验,分析了其宏观结果与基本细观参数之间的影响度;张宝玉等[4]研究了PFC2D平节理模型基本细观参数标定的方法,系统确定了基本细观参数的标定程序,并用实例验证了结果的准确性;Benvenut等[5]指出可以用BP神经网络的方法来标定离散元的基本细观参数;Hsieh等[6]通过数值模拟分析了岩石宏观力学受基本细观参数的变化的规律;陈振鸣等[7]通过试验获得了在一定温度范围内的岩石热力学参数的变化规律,结果表明温度变化会引起热力学参数的变化,但是在温度变化范围较小时,热力学参数的变化可以忽略;徐拴海等[8]对影响岩石导热系数的因素做了研究,表明导热系数与温度、矿物成分等因素有关;王彦丹等[9]研究了在一定温度下混凝土的密度、质量热容以及导热系数对混凝土组成以及细观结构的影响;周昊楠[10]基于Matdem建立了非均质/均质岩石的离散元模型,分析了岩石在高温环境下在加载过程中的损伤演化规律;姜海波等[11]研究了热力学参数对高地温段引水隧洞的喷层拱顶环向应力的敏感度进行了排序。
纵观过往研究发现,国内外学者针对岩石离散元模型的细观参数与宏观力学结果研究以及有关热力学参数的试验研究已较为成熟,但鲜有揭示在受环境高温影响下的热力学参数与岩石力学性能之间的响应关系,以及参数多要素之间交互作用对力学性能的影响。故此,本文采用颗粒离散元程序构建高温条件下岩石数值模型,针对模型热力学参数设计多因素正交试验和响应面试验方案,探寻独立参数及参数间交互作用下对岩石峰值强度的影响,并且建立岩石峰值强度与热力学参数间交互作用下的非线性关系,实现了在高温环境下对岩石峰值强度进行预测。
1 建立模型与试验设计
1.1 建立模型
岩石建模采用平行黏结模型来模拟岩石中颗粒与颗粒之间的接触方式,该模型在ball-ball、ball-pebble等5种接触面上可视为具有一定刚度的平行弹簧,均匀的分布在接触面和中心接触点。当接触处发生相对运动时,能够较好地传递所有类型接触间的力与力矩[12],也更加符合实际工程中的岩石情况。平行黏结中用Fi表示合力,Mi表示力矩,力的向量和力矩的向量可以被分解为法向和切向的分量,如式(1)和式(2)所示[13]:
Fi=Fnni+Fsti
(1)
Mi=Mnni+Msti
(2)
式中:Fn、Mn、Fs、Ms分别代表法向力、法向力矩、切向力以及切向力矩;ni、ti分别为法向和切向的单位向量。
在颗粒离散元程序中,利用内置fish语言建立200 mm×100 mm单轴压缩岩石试样。其中颗粒粒径为0.6 mm~0.9 mm,颗粒密度为2 200 kg/m3,孔隙率为0.16,共生成26 633个颗粒。在温度场下岩石参数标定主要包括基本细观参数与热力学参数。其中基本细观参数是基于最优化算法细观参数标定程序进行扩展和调试的,本课题组已将程序封装可直接输入宏观参数进行细观参数标定[2];热力学参数中导热系数是基于DRE-Ⅲ多功能导热系数测定仪试验测得,温差则通过实际的工程现场测量可得,岩石离散元模型的比热容和线膨胀系数的取值通过文献[14]大致确定,再通过“试错法”确定比热容和线膨胀系数和对岩石强度的影响,运用得到的变化规律并且反复调试,直到得到的与物理试验结果一致的为止。最终温度场下岩石离散元模型见图1,数值模拟与室内物理试验单轴压缩应力-应变比对如图2所示,由图2可知两者应力-应变曲线趋势一致且重合度较高,说明岩石离散元模型中参数选取基本无误,其中具体细观参数见表1,热力学参数表2。

表1 岩石模型细观力学参数

表2 岩石模型热力学参数
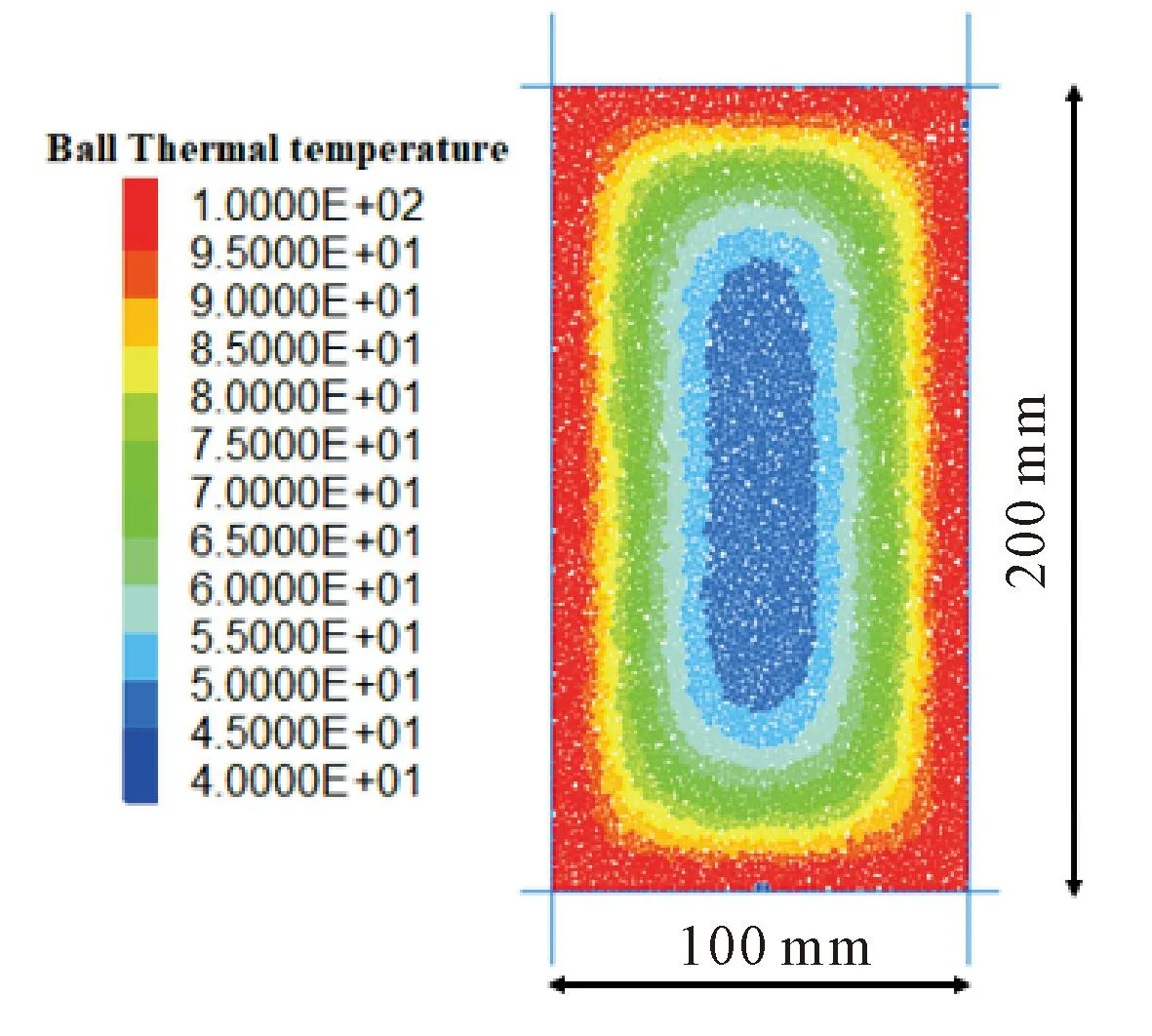
图1 温度场下岩石离散元模型
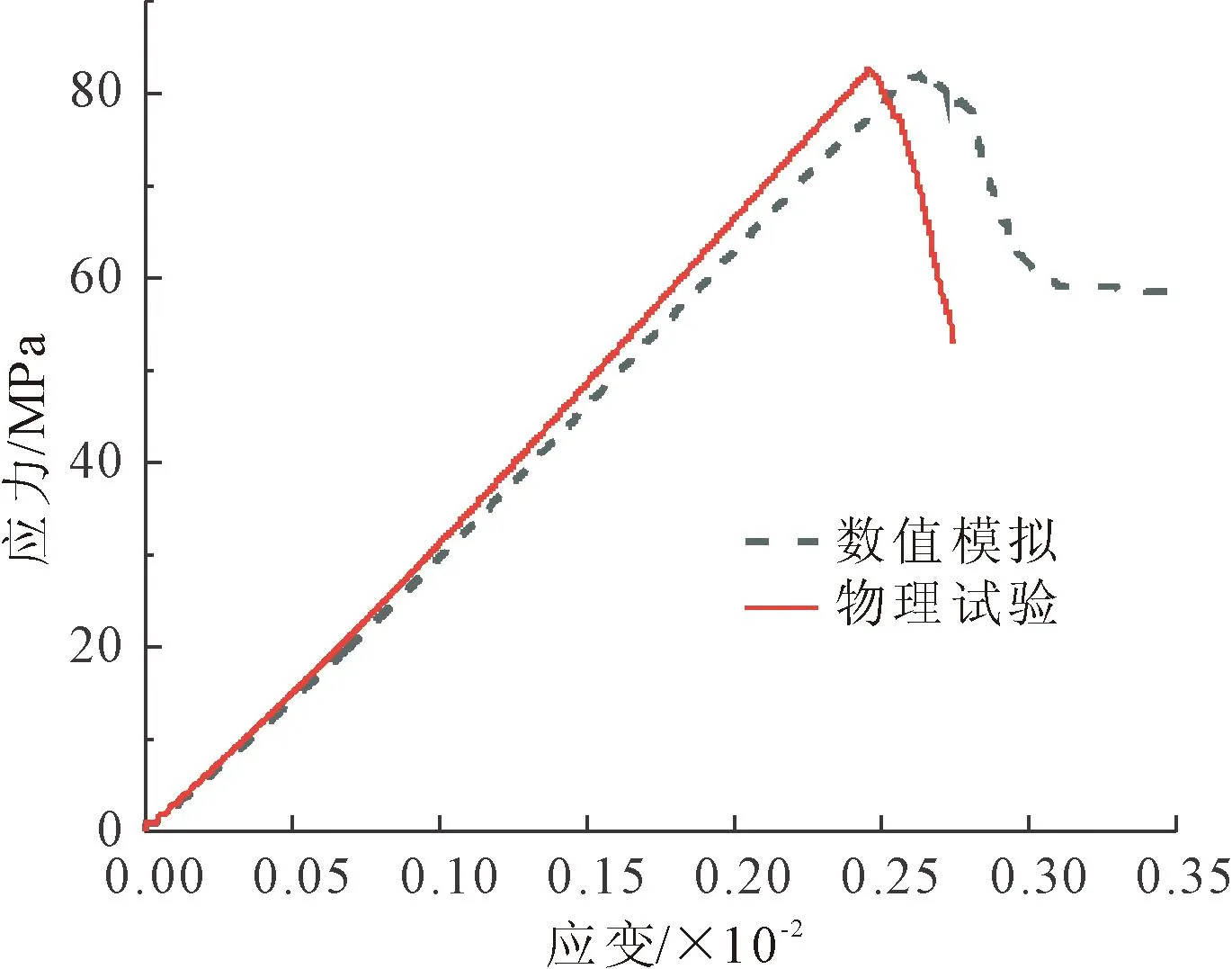
图2 数值模拟与物理试验单轴压缩应力-应变图
1.2 试验设计
在PFC2D热模块中,若要得到岩石峰值强度与热力学参数间的一组映射关系,需要考虑的因素有比热容、线膨胀系数、温差以及导热系数,试验指标为峰值强度。针对这类多水平、多因素问题采用全面试验进行研究将耗费大量时间和精力,故而需要借助试验设计方法合理安排试验以减少试验次数。正交试验设计所选试验点代表性较强[15],能在明显降低试验次数的前提下,给出可靠的研究结论。此外,正交试验设计不仅能够可以筛选出对峰值强度具有显著性影响的岩石热力学参数,而且对峰值强度与热力学参数间的定量关系进行初步估计。
但是正交试验以及多因素方差分析没有考虑参数交互对峰值强度的影响,而响应面设计可以对因变量敏感度高的几个参数进行交互分析,并且它可以对试验指标与因素间的非线性关系进行估计,给出二阶响应面公式。整体试验设计思路如图3所示。
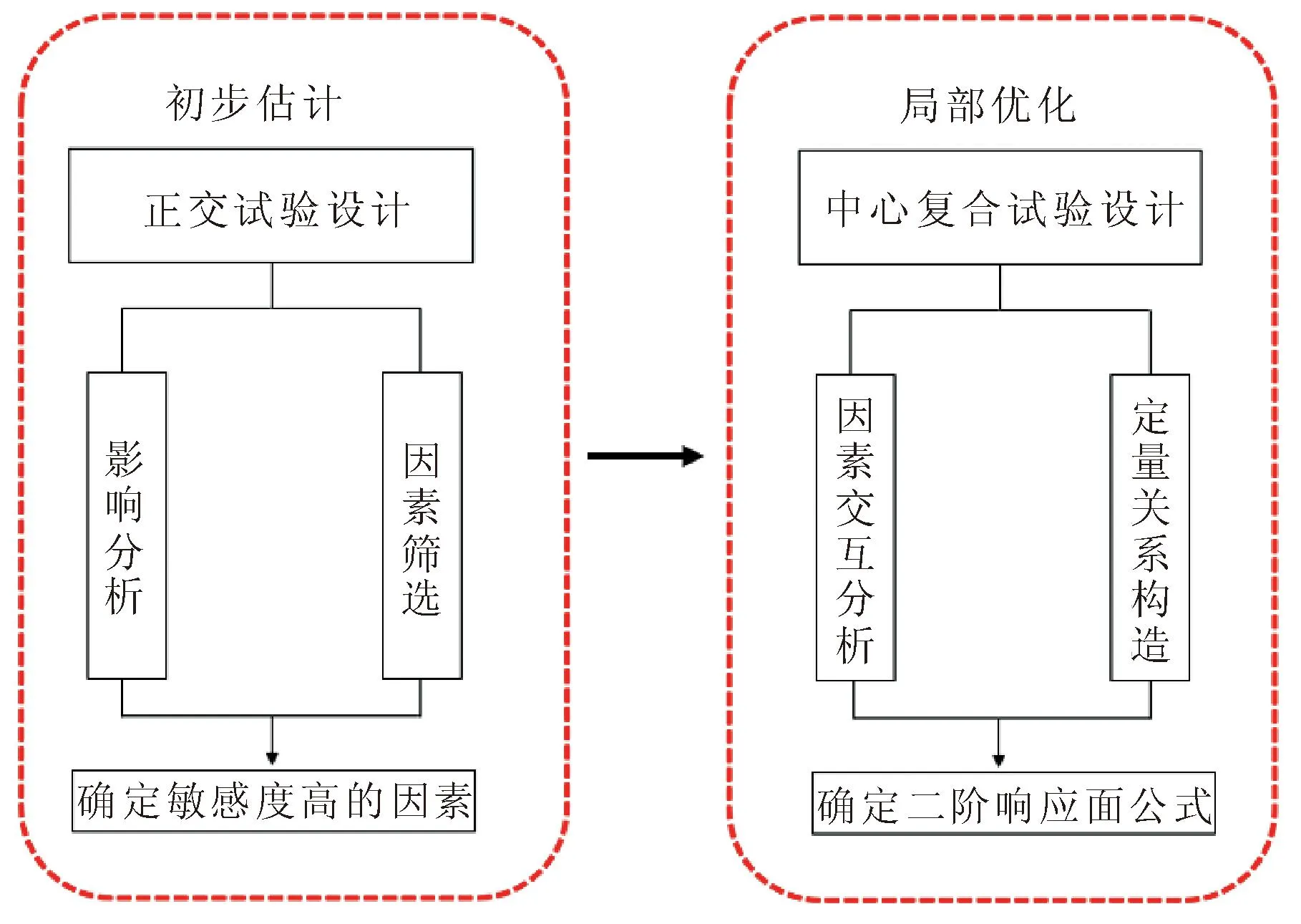
图3 试验设计思路
2 试验结果与分析
2.1 正交试验方案设计结果
通过阅读相关文献[16],并且结合实际工程背景,将岩石主要热力学参数的变化范围进行粗略估计:导热系数取值范围为1 W/(m·K)~4 W/(m·K),线膨胀系数变化范围为(2.0~5.0)×10-5/K,比热容取值范围设定为700 J/(kg·K)~1 000 J/(kg·K),另外假设岩体内部温度与现场环境的温差设定为50℃~80℃。最终确定各个因素水平见表3。在表3基础上设计了PFC模型热力学参数正交序列,最终确定岩石在一定温度下进行单轴压缩数值模拟并得到峰值强度,结果见表4。从表4可以看出数值模拟结果中岩石峰值强度取值范围在34.36 MPa~64.56 MPa,结果均在合理范围以内。
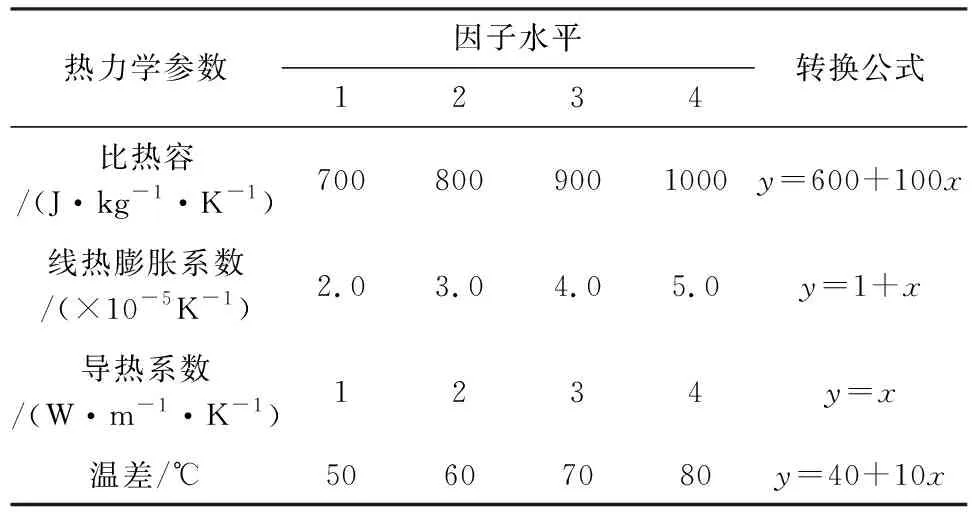
表3 热力学参数正交试验设计表
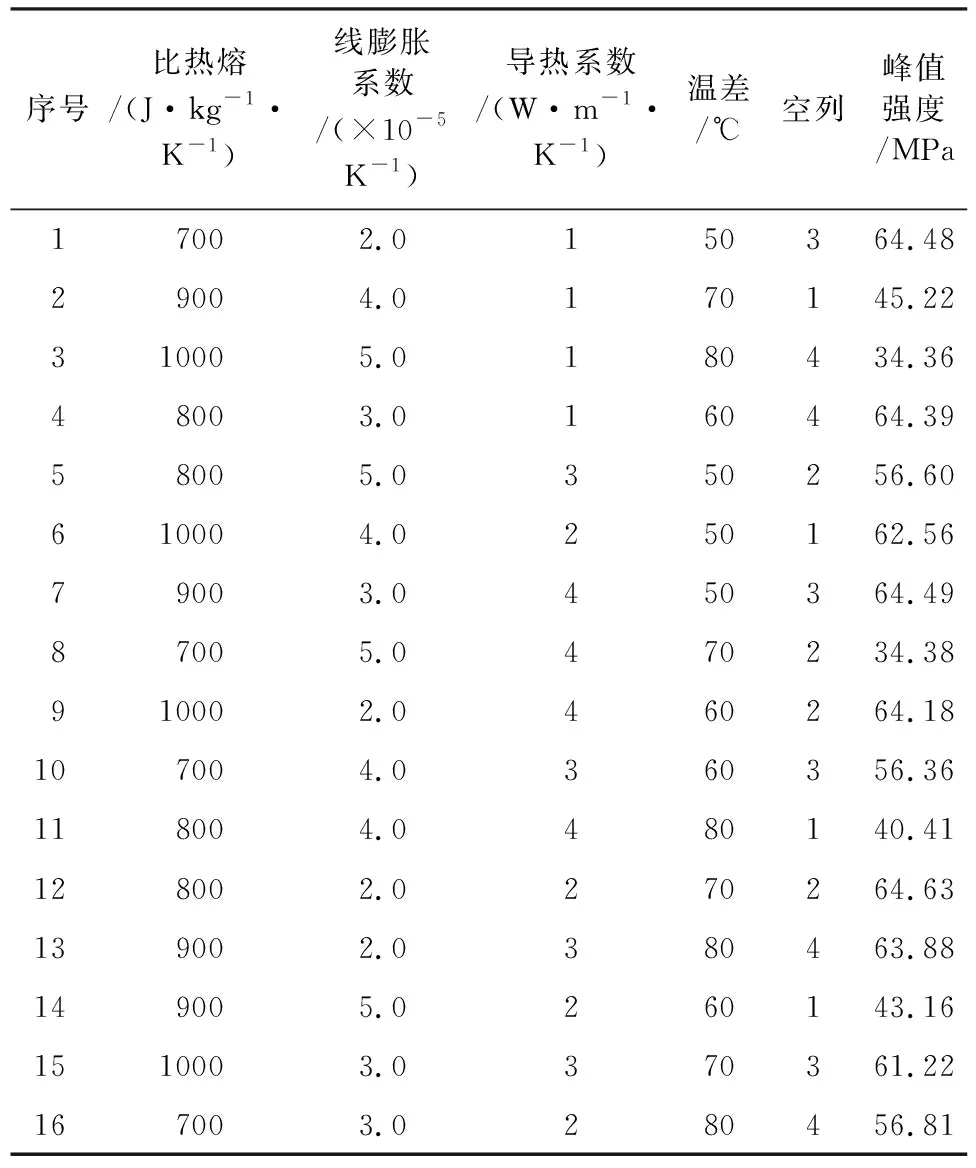
表4 正交设计矩阵序列及岩石峰值强度参数结果表
2.2 热力学参数对峰值强度的独立作用结果
借助Minitab进行极差分析并绘制试验指标平均效果变化趋势图如4所示,由图4(a)、图4(c)可知,随着导热系数和比热容增大,岩石峰值强度随之上下波动,说明导热系数以及比热容对岩石峰值强度的敏感度较低;由图4(b)、图4(d)可知:岩石峰值强度随着线膨胀系数增大而明显减小,这是由于在高温环境下,岩石中的矿物质会发生热膨胀和热收缩,导致岩石尺寸发生变化;此外岩石在高温环境中的矿物质会发生热化学反应,导致岩石中的结构加速发生破坏。随着岩石内外部温差增加,岩石的峰值强度反而减小,这主要是当岩石内外温度差异较大时,导致内部不同部位会产生不同的热应力,当热应力的大小超过岩石材料的强度极限时,岩石就会发生破裂。
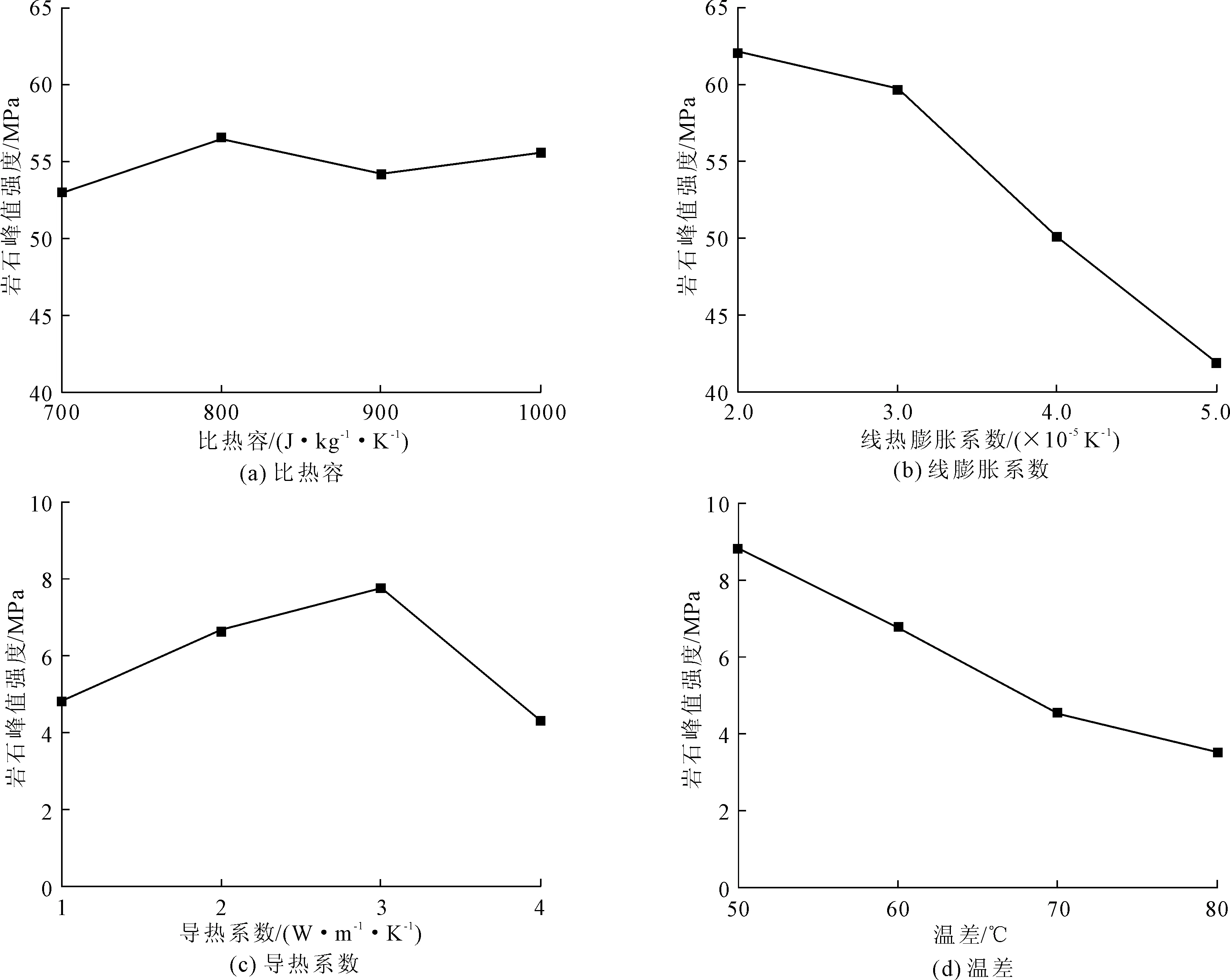
图4 热力学参数平均峰值强度变化趋势
极差分析见表5,由表5可以看出,线膨胀系数、温差、导热系数、比热容极差R分别为22.1675、13.1675、8.65、3.5,热力学参数对岩石峰值强度主次影响因素为线膨胀系数>温差>导热系数>比热容。

表5 极差分析
极差分析不能估计误差的大小,也不能精确地估计各因素的试验结果影响的重要程度[22]。为了研究热力学参数对峰值强度的敏感度,进一步选用多因素方差分析,对各个因素间的主效应进行分析,其中方差分析表见表6。
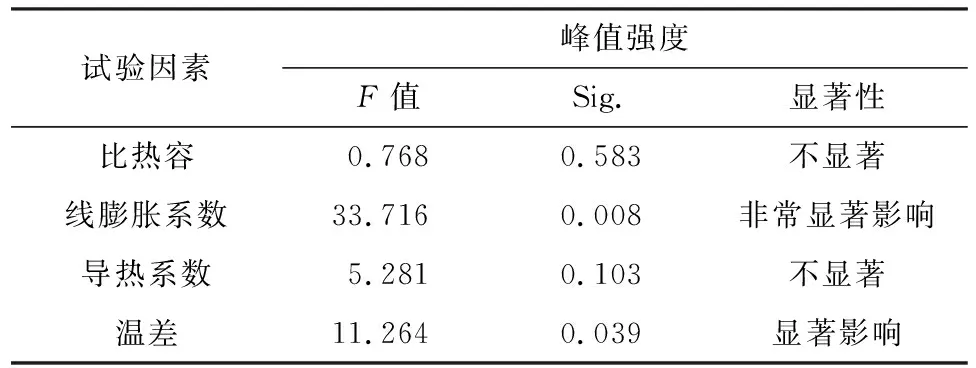
表6 方差分析表
sig.可以用于检验热力学参数是否对岩石峰值强度产生显著影响,假设sig.<0.01,产生非常显著的影响;假如0.01
岩石峰值强度的显著影响主要有线膨胀系数X1、温差X2,对这两个因素与峰值强度y进行线性回归拟合,见式(3),拟合系数R2=0.978,拟合结果较好,具体拟合结果见图5。由图5可知试验序号1实际与拟合峰值强度相差较大,其主要原因是因为序号1的线膨胀系数与温差这两个因素取值分别为2.0×10-5K-1和50℃,都是在因素取值范围最小时进行数值模拟,由图4(b)和图4(d)可知线膨胀系数、温差与峰值强度呈负相关,并且这两个参数对岩石峰值强度影响强度较大,所以相较于其他几组试验误差相对较大。
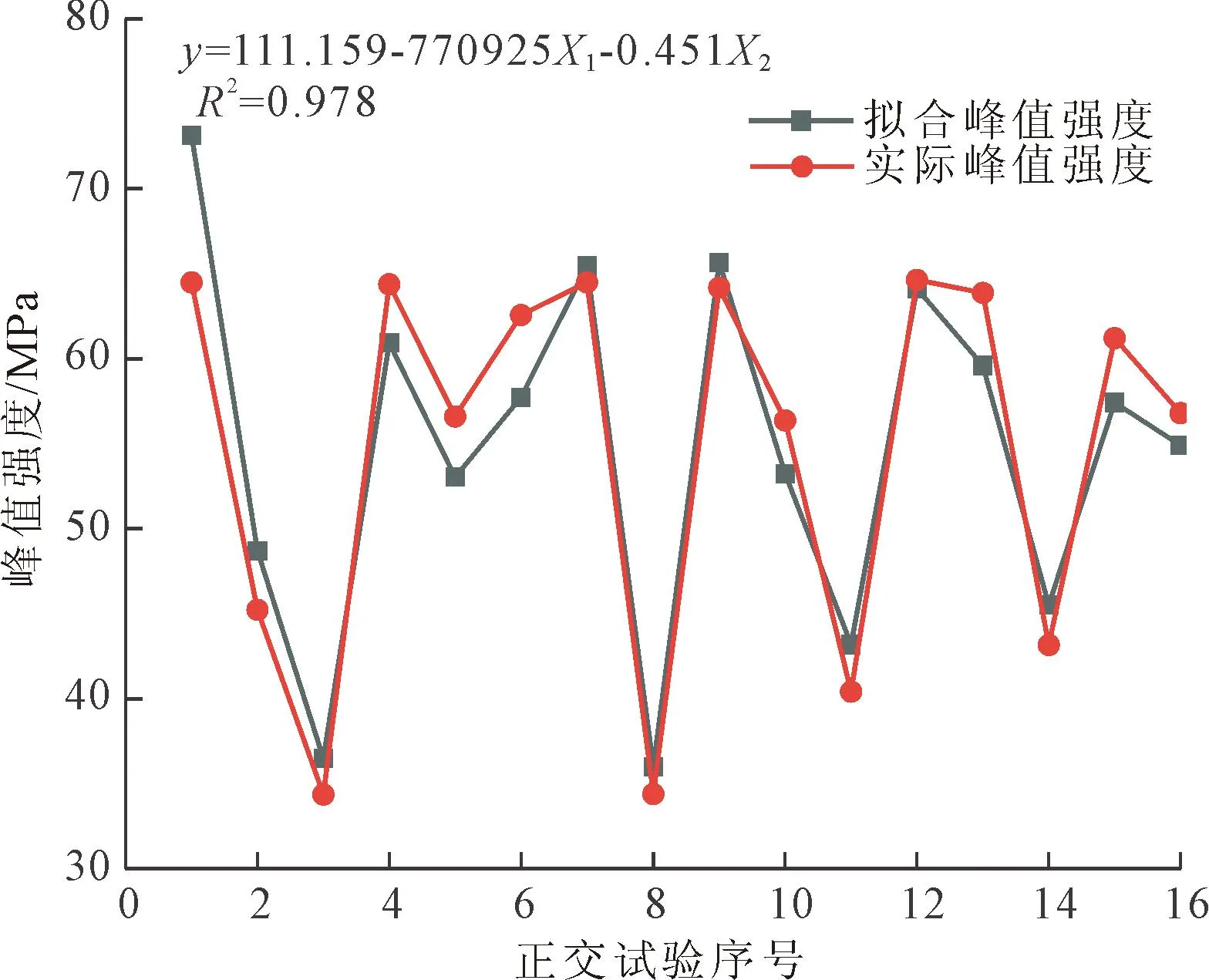
图5 峰值强度与热力学参数拟合
y=111.159-770925X1-0.451X2
(3)
2.3 热力学参数交互作用下对峰值强度的影响
根据正交试验以及多因素方差分析结果可知,对岩石峰值强度有显著影响的热力学参数有线膨胀系数、温差,所以对于设计峰值强度的响应面,只需考虑这两个对峰值强度敏感度高的变量即可。在进行响应面设计时,因素小于3个时应选用Central Composite Design(CCD)试验。具体试验方案见表7,从表7可以看到采用CCD试验方案模拟出的岩石峰值强度取值范围在32.2 MPa~64.46 MPa,结果均在合理范围以内。

表7 CCD试验方案及结果
表8为岩石峰值强度的CCD分析结果,借助Design Expert程序进行响应面设计分析,从结果可以看出线膨胀系数以及温差两个参数交互都对峰值强度的影响比较显著,其中线膨胀系数影响系数>线膨胀系数与温差两参数交互>温差。之后将线膨胀系数X1、温差X2、以及X1×X2与峰值强度y拟合,得到的二阶响应面公式,见式(4),拟合系数R2=0.9911,拟合结果较好,具体拟合结果见图6。由此也可以较好的确定在高温条件下,岩石峰值强度y与它的线膨胀系数X1和温差X2以及X1×X2之间有较强的关系。
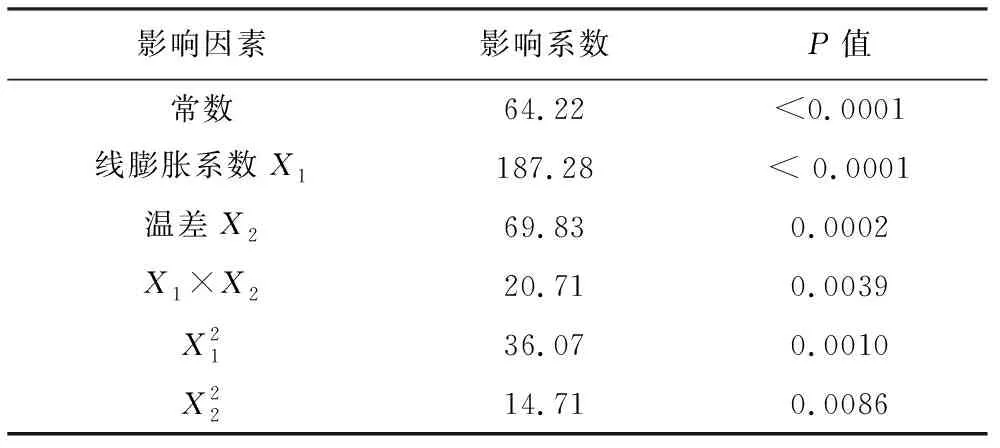
表8 岩石峰值强度CCD试验结果分析
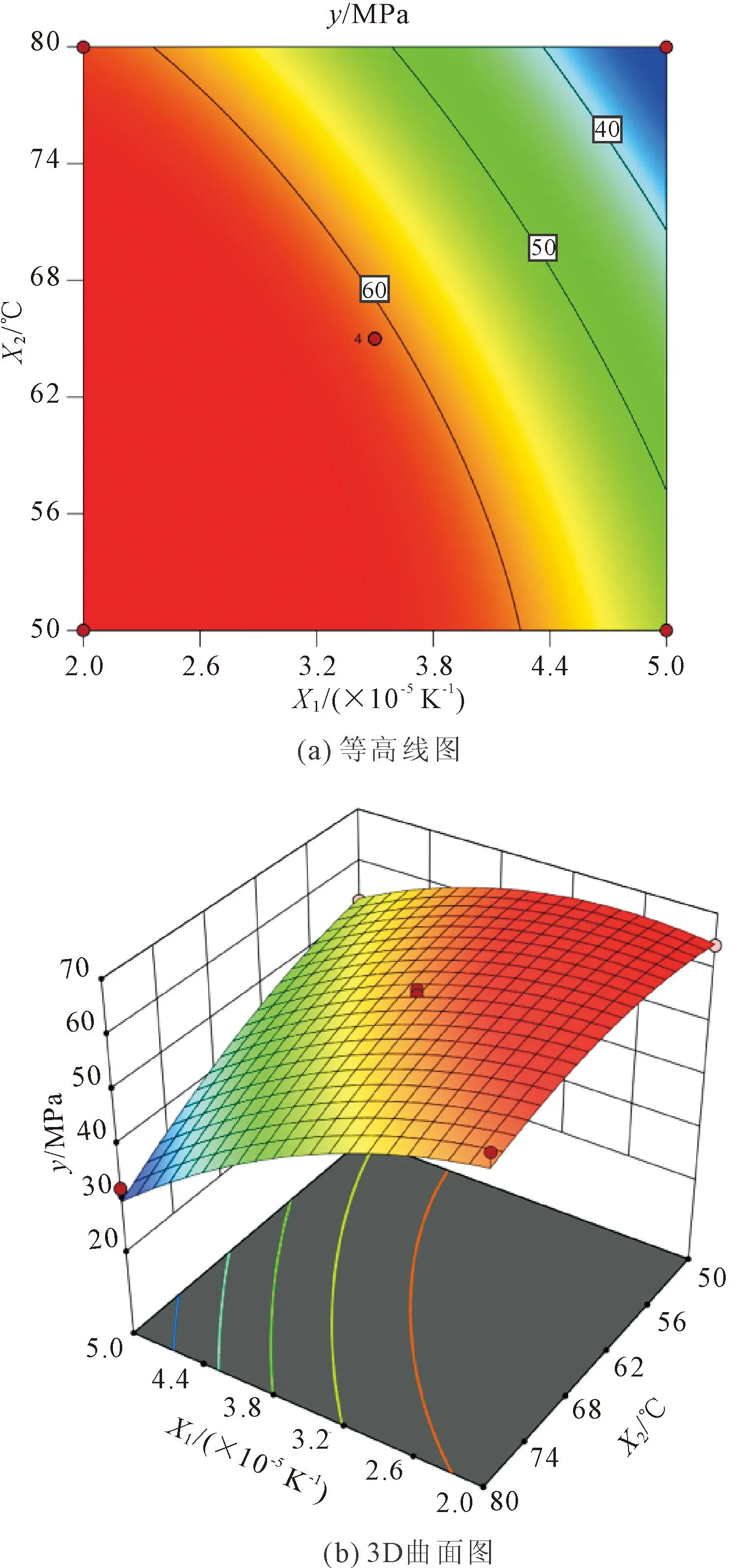
图6 峰值强度与热力学参数的响应面图
(4)
图6的响应曲面是一个坡面[24],图中线膨胀系数(X1)和温差(X2)增大的方向,响应面的高度随之下降,也就是说线膨胀系数(X1)和温差(X2)对峰值强度存在消极的响应,且线膨胀系数(X1)较大时,坡面更加陡峭,说明线膨胀系数(X1)越大对岩石峰值强度(y)影响越显著。
2.4 实例验证
为了验证热力学参数与岩石峰值强度的二阶响应面公式的准确性,对文献[20]中热力学参数进行代入验算。文献热力学参数、文献中岩石峰值强度以及用式(3)计算的峰值强度结果见表9,其中温差为110℃时误差最大为3.0%,主要原因是二阶响应面公式中温差因子水平区间为50℃~80℃,但误差也在合理的范围以内,从而可以证明因素交互作用下的二阶响应面公式可靠。
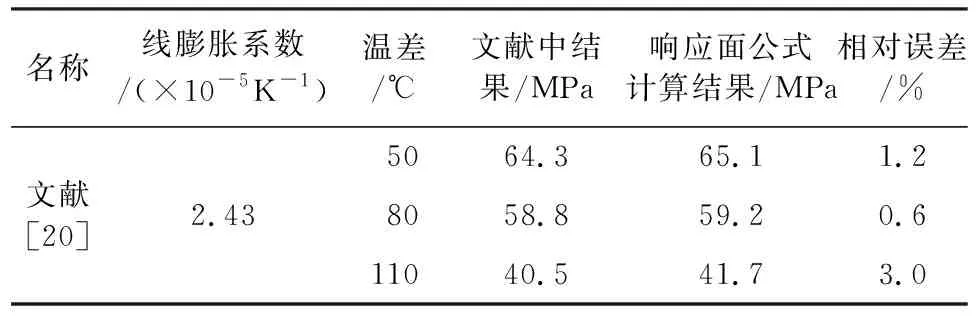
表9 文献结果与响应面公式计算结果对比表
3 结 论
本文通过颗粒离散元程序PFC2D建立了岩石的离散元模型,并基于正交试验设计和中心复合试验设计的思想,研究了岩石热力学参数与峰值强度关系。得到主要结论如下:
(1) 基于正交试验设计,通过颗粒离散元程序PFC2D进行岩石单轴压缩数值模拟,分析4个热力学参数对岩石峰值强度的影响程度,根据其影响进行排序,并建立了峰值强度与热力学参数之间的关系。
(2) 通过多因素方差分析和线性回归得到如下结论:岩石峰值强度主要受线膨胀系数以及温差的影响,且与线膨胀系数、温差均呈负相关关系。
(3) 采用响应面设计方法提出了一定范围内的岩石热力学参数与抗压峰值强度之间的二阶响应面公式,通过二阶响应面计算结果与实例结果相近,验证了本文方法的可靠性。
