基于裂纹诱导弦挠度的梁裂纹损伤识别

欧阳煜, 夏登科, 楚鹏辉

(上海大学力学与工程科学学院, 上海 200444)

起源于航空航天领域的结构健康检测技术在20 世纪80 年代起逐步应用于土木工程领域,同时研究者对建筑结构的健康检测开展了大量的理论与应用研究[1-3], 这些研究成果对保障结构安全运营具有十分重要的意义.目前, 梁中裂纹检测和损伤识别方法大致可以分为局部检测技术和整体检测技术[4].根据损伤识别中施加于结构的荷载不同, 可将全局损伤识别方法划分为基于静力响应的损伤识别方法[5-8]、基于动力响应的损伤识别方法[9-12]以及基于动静力响应的混合测试损伤识别[13-14].

随着测试设备与技术的不断更新和提高, 基于静力响应的结构损伤识别方法逐渐成为运用广泛的全局损伤识别方法, 具有测量精度高, 操作技术简单, 成本低等优点[15-16].梁结构在服役中可能产生各类裂纹, 由于梁正截面强度不足或正应力过大, 将导致梁中产生横向裂纹,如建筑结构的承重梁和PC 斜拉桥等.近年来在梁横向裂纹损伤识别方面, 基于裂纹诱导弦挠度函数的识别方法得到了广泛关注.Caddemi 等[16-17]将开裂纹等效为扭转弹簧, 分别提出了梁中单/多裂纹损伤解析识别方法.Koo 等[18]和Sun 等[19]提出了悬臂型结构的裂纹损伤识别方法.而考虑轴力二阶效应, 孟哲等[20]提出了悬臂梁支承及裂纹参数的识别方法.考虑裂纹缝隙效应, 汪德江等[21]和杨骁等[22]提出了梁中开闭裂纹损伤识别方法.基于裂纹诱导弦挠度函数的构造特征, 杨骁等[8,23]通过拟合分段线性函数, 提出了悬臂梁的裂纹损伤识别方法.

利用裂纹诱导弦挠度函数的构造特征, 本工作提出了基于挠度测量的任意边界条件下Euler-Bernoulli 梁裂纹损伤的静力识别方法.首先, 将裂纹等效为单向旋转弹簧, 得到了任意边界条件下裂纹Euler-Bernoulli 梁静力弯曲挠度的解析通解; 然后, 证明了裂纹诱导弦挠度函数为分段三次多项式函数, 且分段函数的交点坐标即为裂纹位置, 分段函数交点处的斜率改变量与裂纹等效扭转弹簧柔度有关, 并在此基础上提出了利用最小二乘法拟合裂纹诱导弦挠度函数的裂纹损伤识别方法; 最后, 数值验证了本工作提出的裂纹损伤识别方法的适用性和可靠性, 考察了挠度测量误差、裂纹位置和深度等对损伤识别结果的影响.

1 裂纹Euler-Bernoulli 梁的静力弯曲解析通解

如图1 所示, 设长和高分别为L和h、抗弯刚度为(EI)0的Euler-Bernoulli 矩形截面梁承受横向载荷q(x) 的作用, 且在x=xi(i= 1,2,··· ,N) 处存在深度为di的横向开裂纹.将x=xi处的裂纹等效为刚度Ki的扭转弹簧, 则裂纹梁的等效抗弯刚度[16-17,20]为

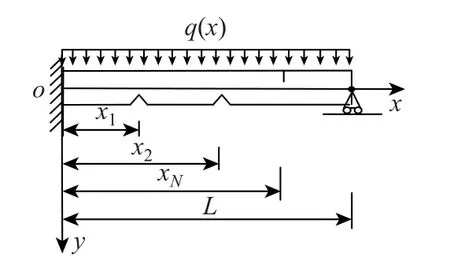
图1 裂纹梁Fig.1 Cracked beam

式中:δ(x) 和H(x) 分别为Delta 函数和Heaviside 函数[8,17,21]; (EI)e为裂纹梁的等效抗弯刚度; 而裂纹的等效扭转弹簧刚度[8,17,24]为

在横向载荷q(x) 作用下Euler-Bernoulli 裂纹梁静力弯曲挠度w(x) 满足的控制方程为

而裂纹梁的弯矩和剪力分别为

引入如下无量纲量和参数,

则无量纲控制方程为

而无量纲弯矩m(ξ) 和剪力fS(ξ) 分别为

利用Heaviside 函数H(ξ) 和Delta 函数δ(ξ) 的性质, 可得控制方程式(7) 的通解为

式中:Ci(i=1,2,3,4) 为待定常数; 而Q[i](ξ) 定义为

从而, 无量纲弯矩m和剪力fS以及裂纹ξ=ξi(i=1,2,··· ,N) 处的弯矩mi分别为

通常, 由梁的4 个边界条件可给出待定常数C1,C2,C3和C4满足的线性代数方程

式中: [A]为4×4 矩阵;{C}={C1,C2,C3,C4}T; 而{b}为常矢量.从而得到裂纹梁挠度w(x)的解析解.

2 Euler-Bernoulli 裂纹梁的裂纹诱导弦挠度

对于无裂纹的完整梁, 即fi= 0(i= 1,2,··· ,N), 由式(9) 及式(12) 可得无量纲挠度WI(ξ) 为

若梁在区间[ξa,ξb]⊂[0,1]中存在l条裂纹, 分别位于ξ=ξi(i=i0+1,i0+2,··· ,i0+l)处, 则区间[ξa,ξb]上的裂纹诱导弦挠度函数WC(ξ)[8,17-18,21]为

式中:WD(ξ) 为裂纹损伤诱导挠度, 定义为WD(ξ)=W(ξ)-WI(ξ).

可见, 裂纹诱导弦挠度函数WC(ξ) 是分段三次代数多项式函数.当区间[ξa,ξb]中不存在裂纹, 即fi= 0(i=i0+1,i0+2,··· ,i0+l) 时, 裂纹损伤诱导挠度WD(ξ) 和裂纹诱导弦挠度函数WC(ξ) 为三次光滑曲线; 当区间[ξa,ξb]中存在l条裂纹, 且mi /= 0(i=i0+1,i0+2,··· ,i0+l) 时, 裂纹诱导弦挠度函数WC(ξ) 为由l+1 条三次多项式函数组成的分段函数,且分段函数曲线的交点即为裂纹位置.同时,WC(ξ) 在裂纹ξ=ξi(i=i0+1,i0+2,··· ,i0+l)处, 裂纹诱导弦挠度WC(ξ) 斜率的改变量即横截面转角的增量为

可见, 若ξ=ξi裂纹处的弯矩mi /=0, 则ξ=ξi处裂纹的等效扭转弹簧柔度fi为

进而, 由式(6) 得到裂纹深度di(i=i0+1,i0+2,··· ,i0+l).至此, 建立了开闭裂纹损伤识别的理论依据.

3 基于挠度的裂纹损伤识别方法

由于裂纹诱导弦挠度WC(ξ) 是由若干三次多项式函数组成的分段函数, 而每个分段的三次多项式至少需要确定4 个常数, 因此每个分段的三次代数多项式至少需4 个挠度测量值才能唯一确定.为识别区间[ξa,ξb]中的裂纹, 初步假定裂纹个数为l个, 将区间[ξa,ξb]分为m≥l+1 个测量子区间, 每个测量子区间内给定n≥4 个挠度测点.则如图2 所示, 区间[ξa,ξb]的挠度测点数量共M=mn+1, 且记测量点ζr(r= 1,2,··· ,M) 处的挠度测量值为, 其中和分别为ζ1=ξa和ζM=ξb处的挠度测量值和

图2 梁挠度测量点ζFig.2 Beam deflection measuring points ζ

在测量点ζr(r=1,2,··· ,M) 处测得挠度值后,由式(13)得到完整无裂纹梁在测点ζr处的挠度WIr, 进而由式(14) 可得到测量点ζr处诱导弦挠度的近似值.由此,寻求近似裂纹诱导弦挠度函数的问题归结为依据测量数据点集合A==1,2,··· ,M}, 寻求最佳分段三次代数多项式函数的拟合.基于最佳分段线性函数的拟合方法[23,25], 建立最佳分段三次多项式函数的拟合, 具体算法如下.

Step 1: 给定拟合误差ε>0, 令NL=1,ms=1,mk=4.

Step 2: 根据测量点数据Ams(ζms),Ams+1(ζms+1k(ζms+mk,WC(ms+mk)), 利用最小二乘法拟合三次函数(ξ)=aNLξ3+bNLξ2+cNLξ+dNL.

Step 3: 如果mk=M,输出裂纹诱导弦挠度函数(ξ)=aNLξ3+bNLξ2+cNLξ+dNL,并且若NL>1, 计算函数

在区间[ζms-1,ζms]中的交点, 从而确定第NL-1 个裂纹的近似位置, 以及利用式(16) 得到该裂纹的近似等效扭转弹簧柔度, 结束计算; 否则, 计算函数WNL(ξ) 在点ζ=ζmk+1处的函数值WCNL(ζmk+1), 并计算

然而，地方财力不足的现状不能必然地导出消费税收入分配机制改革的合理性。税制变革应剖析其背后的理论依据。对此还有必要结合消费税改革进程，探究消费税收入分配机制调整的合理性，检视消费税收入分配机制调整与消费税其他改革措施的关联，以期能为理论研讨与立法调整有所裨益。

Step 4: 如果∆< ε, 即Amk+1(ζmk+1) 位于弦挠度函数WCNL(ξ) 上, 则令mk=mk+1, 并返回Step 2; 否则, 输出弦挠度函数=aNLξ3+bNLξ2+cNLξ+dNL.

Step 5: 令NL=NL+1,ms=ms+mk,mk=4, 返回Step 2, 继续执行.

在裂纹诱导弦挠度函数的拟合过程中, 由于挠度测量存在误差e, 导致计算误差ε确定较为困难.若ε取值不当, 可导致识别到虚假的裂纹, 或遗漏裂纹.所以, 为准确识别裂纹, 应尽可能控制挠度的测量误差e.同时, 应进行初步的判断, 尽量使每个识别区间[ξa,ξb]中只存在一条裂, 如通过逐步二分法识别区间[ξa,ξb], 使得识别区间最多只存在一条裂纹.

4 数值算例

接下来数值模拟本工作提出的梁中开裂纹损伤识别方法的有效性和可靠性.由于不可避免地存在挠度测量误差, 因此为数值模拟测量挠度, 假定挠度测量值[8,20]近似为

式中:e为测量误差;R() 为[-1,1]中的均匀分布随机数.

为描述损伤参数识别精度, 定义裂纹i位置识别误差eloc和等效扭转弹簧柔度识别误差ef分别为

式中:和分别为裂纹i识别的近似位置和裂纹等效扭转弹簧近似柔度.

设固支Euler-Bernoulli 矩形截面裂纹梁长高比L/h=10, 且承受无量纲均布载荷Q0=1的作用, 区间ξ ∈[ξa,ξb]分为m= 5 个测量子区间, 每个测量区段挠度测点n=5, 故[ξa,ξb]上共有M=26 个挠度测量点, 且裂纹损伤参数识别数值算法中的计算误差ε=0.01.

4.1 固支梁存在一个裂纹

图3 当ξ1=0.5 时, 不同裂纹深度d/h 下固支裂纹梁的拟合裂纹诱导弦挠度WCFig.3 Fitted cracked-induced chord deflection WC of clamped cracked beam for different crack depth d/h when ξ1 =0.5

表1 给出了不同测量误差e和不同裂纹深度d/h下识别的裂纹近似位置和裂纹等效旋转弹簧近似柔度分别与其精确位置ξ1和精确裂纹等效扭转弹簧柔度f1的识别误差, 其中eloc和ef分别为裂纹识别近似位置和裂纹等效旋转弹簧近似柔度的识别误差.可见,裂纹越浅, 测量误差越大, 识别精度越低; 裂纹位置的识别精度远高于裂纹等效扭转弹簧柔度识别精度; 随着裂纹深度增加和测量误差的减小, 裂纹位置的识别精度和裂纹等效扭转弹簧柔度识别精度都逐渐提高, 且在测量误差达到1%时, 裂纹等效扭转弹簧柔度识别精度相对较差.

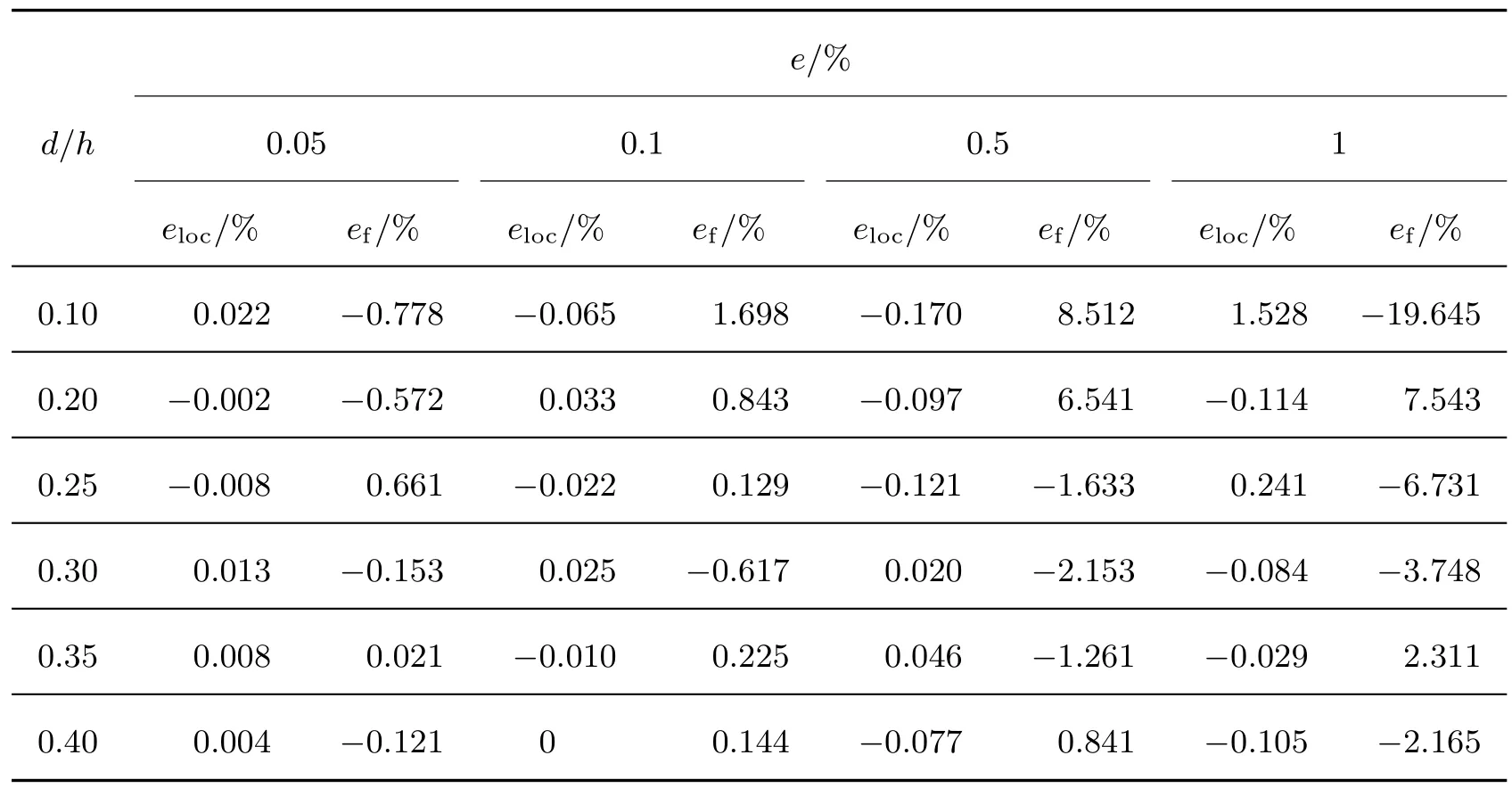
表1 当ξ1=0.5 时, 不同测量误差e 下裂纹损伤参数的识别误差Table 1 Identification errors of crack damage parameters for different measurement errors e when ξ1=0.5

4.2 固支梁存在两个裂纹

下面考虑裂纹个数对裂纹损伤参数识别的影响.设固支梁在ξ1= 0.35 和ξ2= 0.6 处存在深度为d1=d2=d的裂纹, 其他条件同上.图4 和5 分别给出了挠度测量误差e分别为0.05%, 0.1%, 0.5%和1%, 裂纹深度d/h分别为0.10, 0.20, 0.25, 0.30, 0.35 和0.40 时, 在测量区间[ξa,ξb]= [0,0.5]和[ξa,ξb]= [0.4,0.9]内的固支裂纹梁裂纹诱导弦挠度曲线.可见, 在保证裂纹识别区间内仅有一个裂纹的前提下, 裂纹个数不影响裂纹梁诱导弦挠度函数的性质.

图4 当ξ1=0.35 时, 不同裂纹深度d/h 下固支裂纹梁的拟合裂纹诱导弦挠度WCFig.4 Fitted cracked-induced chord deflection WC of clamped cracked beam for different crack depth d/h when ξ1 =0.35

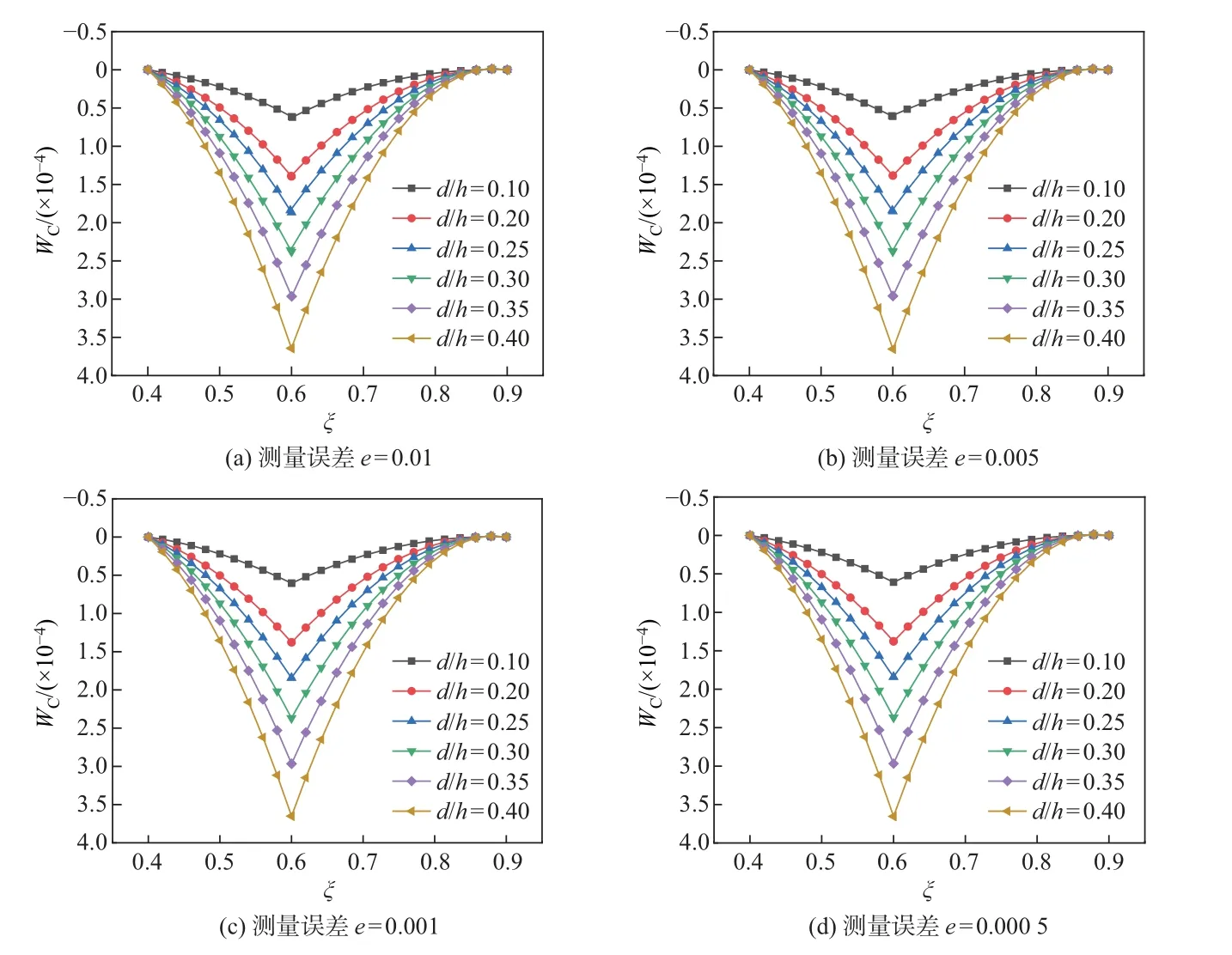
图5 当ξ2=0.6 时, 不同裂纹深度d/h 下固支裂纹梁的拟合裂纹诱导弦挠度WCFig.5 Fitted cracked-induced chord deflection WC of clamped cracked beam for different crack depth d/h when ξ2=0.6

表2 和3 分别给出了不同测量误差e和不同裂纹深度d/h下识别的裂纹近似位置和裂纹等效旋转弹簧近似柔度分别与其精确位置ξ1,ξ2和精确裂纹等效扭转弹簧柔度f1,f2的识别误差.对比表1 可知, 在保证裂纹识别区间内仅有一个裂纹的前提下, 裂纹个数对开裂纹参数的识别精度影响有限.

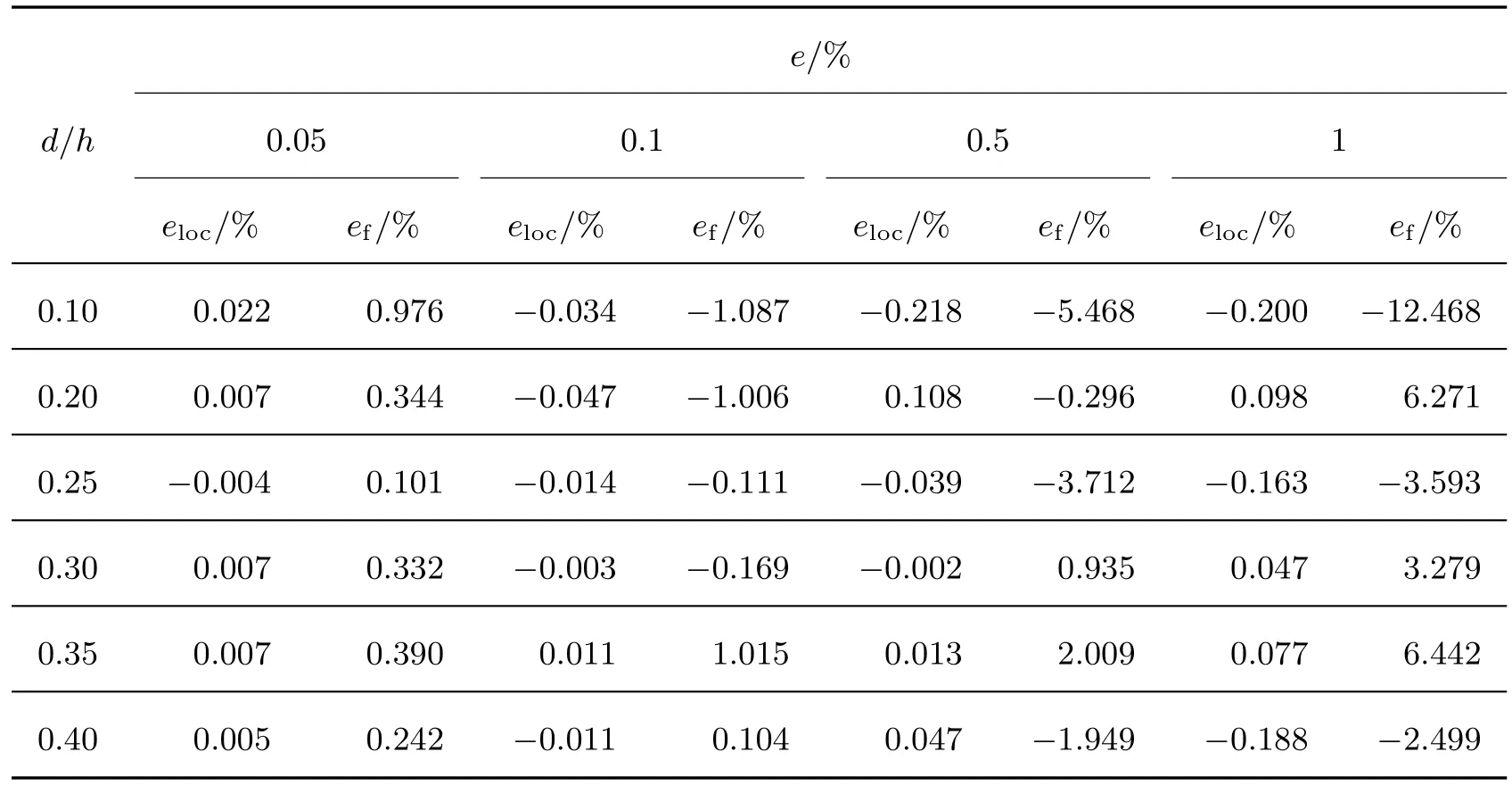
表2 当ξ1 =0.35 时, 不同测量误差e 下裂纹损伤参数的识别误差Table 2 Identification errors of crack damage parameters for different measurement errors e when ξ1 =0.35

同时, 数值模拟结果表明, 在识别区间内仅有一个裂纹的前提下, 裂纹识别区间[ξa,ξb]的选取不影响诱导弦挠度曲线的性质, 即裂纹诱导弦挠度曲线为分段三次多项式函数, 只影响其大小, 并且对裂纹位置及等效扭转弹簧柔度的识别结果影响有限.可见, 本工作提出的开裂纹损伤识别方法具有较好的鲁棒性.

5 结 论

本工作提出了基于裂纹诱导弦挠度的Euler-Bernoulli 梁横向裂纹静力损伤识别方法.首先, 将裂纹等效为线性扭转弹簧, 利用Delta 函数和Heaviside 函数, 得到了任意边界条件下裂纹Euler-Bernoulli 梁静力弯曲挠度的解析通解; 然后, 推导出裂纹诱导弦挠度的表达式, 发现裂纹诱导弦挠度函数为分段三次多项式函数, 并基于裂纹诱导弦挠度函数的性质, 利用最小二乘法拟合裂纹诱导弦挠度函数, 提出了基于挠度测量的裂纹位置和裂纹等效扭转弹簧柔度的数值识别方法; 最后, 数值验证了本工作提出的裂纹损伤识别方法的适用性和可靠性, 考察了挠度测量误差、裂纹位置和深度等对损伤识别结果的影响, 得到如下结论.

(1) 基于裂纹诱导弦挠度函数的裂纹位置和裂纹损伤程度识别方法避免了基于有限元的裂纹识别方法的非线性方程组的求解, 且裂纹数量及裂纹识别区间的选取对裂纹损伤识别结果的影响有限, 具有较强的鲁棒性.

(2) 当区间只含有一条裂纹时, 诱导弦挠度函数曲线由两段三次多项式函数曲线构成, 裂纹位置为两段曲线交点横坐标, 且裂纹处裂纹诱导弦挠度斜率改变量随着裂纹深度的增加而增大.

(3) 裂纹位置的识别精度高于裂纹等效扭转弹簧柔度的识别精度.同时, 为控制识别误差,应严格控制测量精度.

(4) 对于连续梁, 裂纹诱导弦挠度仍为分段三次多项式形式, 因此本工作提出的方法适用于连续梁的裂纹损伤识别.