基于全寿命周期的隔震结构整体性优化

段博洋, 朱杰江

(上海大学力学与工程科学学院, 上海 200444)

传统抗震设计理念以保障生命安全为首要目标, 设防目标为“小震不坏, 中震可修, 大震不倒”, 很少考虑因地震破坏而引起的巨大经济损失.大震不倒并不能保证恢复结构的使用功能及安全, 结构可能在震后不可修复[1], 因此必须采用更加合理的方法来处理初始成本和预期损失之间的关系.随着技术的革新以及设计方法、建筑材料的进步, 人们开始追求高的经济性、安全性、易维护性和舒适性等目标性能, 故基于性能的抗震设计理论在这种背景下产生了.

基于性能抗震设计思想的提出, 改变了以往抗震规范以生命安全为原则的单一设计方法,业主能够在结构抗震性能和震后修复费用之间寻找到最佳的平衡点[2].隔震作为一项重要的结构控制技术, 可以较好地与基于性能的抗震设计相结合, 自20 世纪90 年代以来, 很多学者对隔震结构的参数优化设计方法和优化算法进行了研究与探讨, 马玉宏等[3]充分考虑了隔震结构在地震作用下的变形特点, 提出了隔震结构全寿命周期成本的评估模型, 直观且定量地分析隔震结构的抗震性能, 证实了隔震结构在全寿命期内具有较好的经济效益; 洪邵文等[4]根据建筑结构隔震设计的特点, 研究了基于成本-效益指标的隔震支座参数优化问题, 提出了以成本-效益指标为目标函数的隔震支座参数优化方法; Wang 等[5]评估了全生命周期内采用基础隔震技术的天然气储存罐的总成本, 研究了地震烈度等级对隔震结构总成本最小化的影响, 并提出了一种新型的评估方法.上述研究表明, 成本-效益准则综合考虑技术、经济、社会和政治等诸多因素, 通过比较工程的全部成本和总效益来评估工程价值[6]; 基于性能的隔震结构在进行优化设计时, 如果采用成本-效益准则作为目标函数, 则可以保证隔震结构在满足既定设计功能的前提下使得工程整体的经济效益明显优于传统的抗震结构.

隔震结构的设计主要包括隔震层设计与上部结构的设计, 目前普遍采用分部设计法来设计基础隔震结构, 即根据设定的抗震目标反复试选隔震支座, 直到结构响应满足所有的规范指标为止.分部设计法最大的优点在于可以利用有限元设计软件来完成上部结构的设计[7], 但是该方法将上部结构与隔震层分开设计, 无法将隔震结构作为一个整体来评估其经济价值, 因此有必要提出基于性能的基础隔震结构整体性抗震设计方法.本工作根据隔震结构的设计特点,以上部结构梁柱截面尺寸和隔震支座参数作为设计变量, 基于成本-效益准则对设计变量进行整体性优化, 期望在保证隔震结构设计目标的前提下, 以最小的成本获取最优的隔震效果.另外, 通过建立优化模型, 采用免疫遗传算法对算例进行优化研究, 验证了隔震结构比传统抗震结构在全寿命周期内更具优势, 并间接证明了本优化方法的可行性.

1 基础隔震结构全寿命成本

美国军方于20 世纪60 年代提出了全寿命周期成本(life-cycle cost) 这一概念, 随后将其应用于军用器材采办并迅速推广至民用企业.在评估结构全寿命周期内成本时, 涉及到结构初始费用、维修费用与损失费用的总费用问题, 由于这3 项费用处于结构全寿命周期内的不同时刻, 因此需要考虑贴现率, 将未来的费用转化为现值, 用以评估总费用的现值.隔震结构在全寿命周期内成本投入的期望值WISO为

式中:CI为隔震结构的初始造价;CM为隔震结构养护维修费用;CF为失效损失费用, 包括直接损失、间接损失还有人员伤亡损失等, 失效损失费用的评估不仅仅是工程问题, 还涉及政治、经济、社会和人道等诸多因素, 因而难以对其进行准确的评估;t为结构的使用年限;λ为贴现率;n代表维修次数.

确定合理的贴现率对可持续性发展, 特别是代际公平分配自然资源相当重要, FEMA 227(1992) 建议公共建筑年贴现率取3%∼4%, 非公共建筑取4%∼6%.本工作结合当前中国经济发展情况, 选用基准收益率作为贴现率, 同时假定结构的初始造价、修复费用等均采用不变的价格计算, 如果不考虑通货膨胀, 则贴现率的计算公式为

式中:i1为年贷款利率, 以2021 年12 月的银行短期年贷款利率为基准, 取i1为4.35%;i2为年风险贴现率, 参考建筑行业统计数据, 取i2为2%.因此, 在不考虑通货膨胀的前提下计算得到λ为6.44%.

1.1 隔震结构初始成本

《建筑抗震设计规范》(以下简称《抗规》)[8]第12.2.7 条规定: 隔震后上部结构的抗震措施可适当降低, 一般以水平向减震系数0.40 为界, 并明确降低的要求不得超过一度.因此, 一个合格的隔震结构初始成本往往由降级设计后上部结构的造价CS和采取隔震措施后所增加的费用Ciso组成, 隔震结构的初始费用表达式为

式中:CS为降级设计后的上部结构造价, 包括混凝土造价、构件配筋造价、箍筋造价和楼板造价;Ciso为采用隔震措施而增加的费用(主要包括隔震支座费、设计费、构造措施费及施工费等);Cc、Cs、Csv和Cf分别为混凝土单价、钢筋单价、箍筋单价和每立方米楼板造价;Nc和Nb分别为框架梁、柱的个数;N为楼层数;Bk和Dk分别为第k个构件矩形截面的宽度和高度;lk为第k个构件的高度(跨度);Ask、A′sk和Asvk分别为第k个构件纵向受拉钢筋、受压钢筋和箍筋的截面积;s为箍筋间距;ρ为钢筋密度.

1.2 隔震结构损失费用

通常把结构到达某一极限状态的失效概率Pf, 例如最大层间位移角或最大层相对加速度的失效概率, 转化为结构在不同地震烈度下各破坏等级的发生概率, 也就是说结构失效概率需要通过极限状态易损性概率和一定地震动发生概率的乘积得到, 故隔震结构的预期损失费用CF可以表示为

式中:CL(Di) 为各等级Di破坏所对应的震害损失;P(Di|Id,Ij) 为设防烈度Id的建筑物在地震烈度Ij下发生Di级破坏的易损性概率;P(Ij) 为某一地震动的发生概率.本工作针对基于性能的抗震设计方法特点并结合我国抗震规范, 对结构构件提出了5 种性能水准(破坏状态): 基本完好D1、轻微破坏D2、中等破坏D3、严重破坏D4和倒塌D5, 具体对应的破坏指标如表1 所示.

表1 基础隔震结构性能控制指标Table 1 Performance control index of base-isolated building

1.2.1 震害损失

震害损失由经济损失和人员伤亡损失2 部分组成.其中经济损失包括直接经济损失、间接经济损失和人员伤亡损失.表2 给出了各破坏等级Di所对应的震害损失CL, 其中CI与NP分别为隔震结构的初始成本和总人数;a、e和d分别为间接经济损失比、救灾投入比和室内资产与结构造价比[9].

表2 钢筋混凝土结构的震害损失Table 2 Expected loss of RC structures 万元

1.2.2 极限状态易损性概率

目前, 很多研究人员基于Park 和Ang 提出的损伤指数模型建立了隔震结构的地震损伤模型, 采用概率密度演化理论[10]或基于动力可靠度的易损性分析方法, 通过理论计算分析和试验分析来确定给定设防烈度下隔震结构的失效概率, 这样就可以把结构的失效概率转化为结构各个破坏等级的发生概率:

式中:Pk为第k层发生Di级破坏的概率;p(D,t) 为概率分布函数.许多研究人员已对传统结构的层间位移角、顶点位移等概率分布函数做了大量研究, 可直接通过相应方法的计算结果代入式(5) 来计算隔震建筑上部结构相应破坏等级的发生概率.

1.2.3 地震动发生概率

我国地震烈度概率符合极值Ⅲ型分布, 引入50 年内超越概率10% 所对应的基本烈度I0(一般情况下, 取设防烈度Id为基本烈度I0), 推导可得地震烈度危险性曲线表达式为

式中:κ为地震形状参数, 我国对应地震危险特征区划为Ⅰ区,κ取值为6.87;ω为地震最大烈度, 取12[11].

根据所取的设防烈度Id和形状参数κ值, 可求出给定烈度Ij对应的超越概率值P(I≥Ij), 进而由式(6) 求得烈度为Ij的地震动发生概率P(Ij) 为

1.3 隔震结构维护费用

考虑到隔震支座在使用寿命内的老化损伤, 本工作对传统抗震结构维修费用CRB与结构反应之间的静态分段线性近似函数做出了适当的调整,即令隔震结构的维修费用CM=αCRB,根据工程经验,α值一般取1%∼3%.基础隔震结构的维修费用CM与结构响应之间的线性分段函数表达式为

式中:δu为隔震结构顶点位移;δus为结构屈服位移;δub为结构极限位移;CS为上部结构重建费用, 即降级设计后的上部结构造价.

2 隔震结构优化模型

《抗规》中规定: 水平向减震系数是指隔震结构与非隔震结构最大层间水平剪力的比值,当水平向减震系数Cβ,DBE<0.4 时, 降低一度设计隔震建筑的上部结构.考虑到隔震体系的隔震层与上部结构是整体协调运作的, 因此根据成本-效益准则, 同步确定隔震层参数和上部结构截面尺寸, 对隔震结构进行整体性优化设计, 从而满足建筑安全性、功能性和经济性等多方面的要求, 避免出现顾此失彼的现象.根据上述设计特点, 以上部结构梁柱截面尺寸和隔震器参数作为优化模型的设计变量, 将隔震结构与传统抗震结构的全寿命成本比µiso/non作为成本-效益指标, 同时希望结构在地震作用下的层间位移尽量小, 且隔震层位移不超过设计允许值.优化模型可以表示为

式中:X为隔震层的一组设计变量;as为屈服强度比[12];η为隔震层铅芯含量[13];Bi和Di分别表示梁、柱构件截面尺寸;WNON为抗震结构的全寿命成本;θk是最大层间位移角, 应小于《建筑抗震设计规范》的规范限值θlim;Uiso,MCE为罕遇地震下隔震层最大水平变形;Ucr为罕遇地震下隔震层的允许位移;VW为隔震结构所遭受的风荷载;Qtot为隔震层总屈服力.

2.1 优化变量

本工作将隔震层划分成4 个区域, 编号分别为①、②、③和④, 隔震层四周区域布置铅芯叠层支座(lead rubber bearing, LRB), 内部区域布置天然橡胶支座(linear natural rubber bearing, LNR), 同一区域内随机放置相同规格的隔震支座, 不同区域的支座布置情况则互不干扰, 这样的布局既能增强结构的抗扭能力, 又能有效消耗地震能量.其中, 铅芯叠层支座的性质主要由屈服前刚度KR、屈服后橡胶水平刚度KP和屈服剪力Qd来确定, 天然橡胶支座的性质主要由橡胶水平刚度KP来确定, 上述指标决定了隔震层消能减振效果, 为隔震层功能性优化提供了设计依据.因此, 模型将屈服强度比as(as=Qtot/((ms+mi)g)) 和铅芯含量η作为设计变量.实际工程中采用的隔震支座为定型产品, 通过配合使用不同型号的铅芯叠层支座和天然橡胶支座来布置隔震层, 即可实现上述2 个参数的变化, 从而获得理想的as值和η值.图2 为铅芯隔震支座的双线性模型, 图中Keq、uy、um和Fm分别为LRB 支座的等效刚度、屈服位移、最大设计位移和最大设计力.

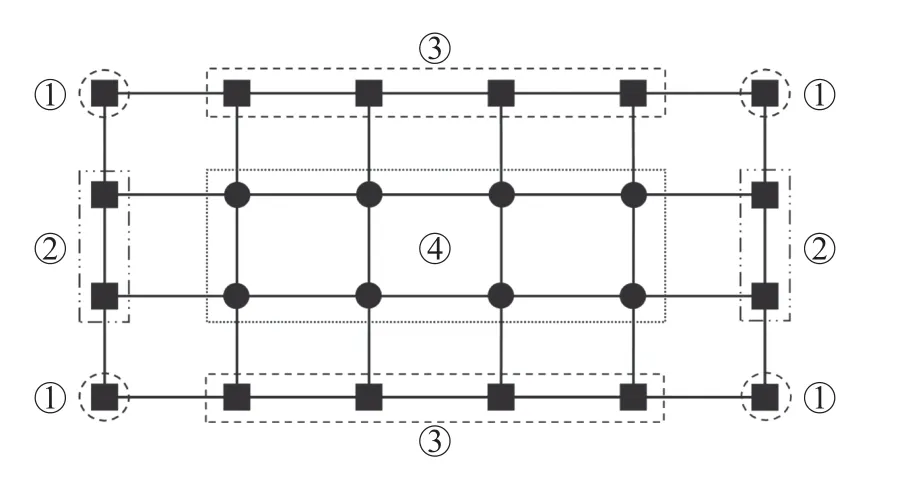
图1 隔震层支座布局划分示意图Fig.1 Layout diagram of isolation bearings

图2 LRB 隔震支座双线性模型Fig.2 Hysteresis model of LRB isolation bearing

除隔震支座以外, 梁、柱构件截面尺寸也对降低结构造价起到了关键性的作用.假设混凝土框架结构有Nb组梁、Nc组柱, 则优化对象为梁、柱截面高与截面宽:Bbi、Dbi(i= 1,2,··· ,Nb),Bcj、Dcj(j= 1, 2,···,Nc).综上所述, 本工作兼顾了隔震层参数和构件截面尺寸参数.

2.2 优化目标函数

模型优化目标为在满足约束条件下使成本-效益指标最小.为了全面综合地评价隔震结构的成本和效益, 成本-效益指标被定义为隔震结构与传统抗震结构的全寿命成本比.一个合格的隔震体系优化设计方案, 其成本-效益指标µiso/non通常介于0∼1 之间,

2.3 约束条件

基础隔震结构在设防地震(design-based earthquake, DBE) 下的设计目标是确定合理的水平向减震系数Cβ,DBE, 以便上部结构实现降低一度设计; 在罕遇地震下的设计目标是确保隔震层水平变形Uiso,MCE不超过隔震支座的变形限值Ucr, 因此将这2 个指标作为优化模型的约束条件是必要且合理的.此外《抗规》中还规定: 风荷载作用下的隔震层水平剪力设计值应小于隔震层总屈服力, 即VW≤Qtot, 因此本工作的优化程序将隔震层总屈服力作为约束条件, 确保隔震结构在迭代优化中不至于出现风荷载作用下的倾覆现象.

《抗规》虽然给出了等效剪切型隔震结构水平向减震系数的简化计算方法, 但仍具有一定的局限性, 当隔震后结构基本周期TISO>5Tg时, 水平向减震系数难以确定, 需要进行专门的研究.隔震结构和传统抗震结构层间剪力最大值在上部结构的首层, 且多自由度(degree of freedom, DOF) 体系的上部结构可以通过模态转换转化为单自由度体系, 因此基础隔震结构可简化为如图3 所示的双自由度简化模型.

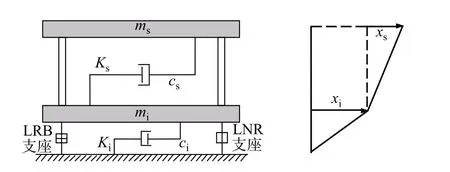
图3 双自由度简化模型Fig.3 2 DOFs model of base-isolated structures

图3 中,ms、Ks和cs分别为上部结构的质量、侧向刚度和阻尼系数;mi、Ki和ci分别为隔震层的质量、水平等效刚度和等效阻尼系数.参照文献[14], 基于振型分解反应谱法可推导求得水平向减震系数和隔震层最大水平变形.水平向减震系数和隔震层最大水平变形分别为

式(11) 和(12) 中的SDBE(ω,ζ) 和SMCE(ω,ζ) 分别表示为设防地震作用下和罕遇地震作用下的规范加速度反应谱的谱值;ω1和ω2为该隔震结构的1 阶和2 阶模态圆频率:

式中:ζ1和ζ2为该隔震结构的1 阶和2 阶模态阻尼比,

ωs为上部结构的自振圆频率,ωs= (Ks/ms)1/2;ωi为隔震结构整的自振圆频率,ωi=(Ki/(ms+mi))1/2;γ和λ分别为上部结构和隔震结构之间的频率比和质量比,γ=(ωi/ωs)1/2,λ=ms/(ωi/ωs)1/2;ζs和ζi分别为上部结构和基础隔震结构的阻尼比,ζs=cs/2msωs,ζi=ci/(2(ms+mi)ωi).

3 隔震结构优化程序

3.1 优化程序概述

本工作基于改进的免疫遗传算法, 在C# 环境中依靠SAP2000 有限元软件的结构分析功能及其开放应用程序接口, 编写了框架混凝土隔震结构优化程序GA-ISB.EXE.程序由3 个模块组成: 前处理模块、遗传算法模块和成本计算模块.程序启动后首先运行前处理模块, 读取SAP2000 初始模型的基本信息及参数, 并规范化初始模型, 方便后续迭代操作; 之后则进入遗传算法模块, 该模块为程序的核心模块, 程序以结构全寿命成本作为适应度值的基础, 通过SAP2000 的2 次开发接口进行模型的修改以及内力计算, 优化过程中反复进行内力提取、构件配筋计算及构件造价计算, 根据遗传算法的步骤对基础隔震结构的隔震层和梁柱构件截面尺寸同时进行优化, 最终迭代出隔震结构全寿命成本最优解; 结构全寿命成本计算模块则依附于遗传算法模块, 其主要作用是返回染色体所对应的结构造价, 即根据造价计算出适应度值返回给遗传算法模块.

3.2 免疫遗传算法

遗传算法是一种模拟生物进化过程的优化算法, 通常被用来优化复杂或多维的目标函数问题[15-16], 其基本原理是效仿物种选择学说和达尔文进化论的法则对种群进行选择, 从而实现随机搜索和优化.该优化算法的基本思想为基于解集种群, 如撒网一般在解空间中进行搜索, 利用种群的历史信息进行种群的迭代进化, 智能推断出潜在高适应度值的下一代种群集合, 最后收敛到一个符合最优适应度值的解.本免疫遗传算法主要有以下几个组成部分.

3.2.1 种群初始化

采用二进制编码的方式生成染色体个体, 等位基因由二值符号集{0, 1}组成, 编码内容主要包括: 隔震支座的规格、柱截面尺寸和梁截面尺寸.算法会随机生成若干个由优化变量组成的染色体, 然后将多个染色体组合形成种群, 这个过程即为种群初始化.种群规模的大小直接影响种群的进化, 种群规模过小不利于实现种群的多样化, 进而影响遗传算法的优化性能; 种群规模过大则会增大遗传算法的计算量, 降低算法的优化效率, 因此种群规模不宜过大也不宜过小, 建议取值为10∼100.

3.2.2 免疫算子

随机生成的染色体可能会出现以下情况: ①梁截面宽大于柱截面宽; ②第k+1 层柱截面尺寸大于第k层柱截面尺寸.上述情况在实际工程中是不存在的, 大量无效的染色体会影响算法的收敛方向, 使算法最终收敛到一个不可行解, 因此需要引入免疫算子来解决模型几何约束问题.

免疫算子作用在适应度函数计算和遗传操作之前, 根据约束条件对染色体中不满足规则的基因进行调整, 避免优化过程中的无效操作.针对上述问题的调整方法为①若梁截面宽Bb大于柱截面宽Bc, 则梁截面宽更替为柱截面宽减50 mm; ②从下至上, 如果第k+1 层柱截面尺寸大于第k层柱截面尺寸, 则调整第k层柱截面尺寸与第k+1 层柱截面尺寸相同, 同时为了避免因顶层柱截面过大而导致下层没有变截面的可能, 顶层柱截面尺寸设置为该类构件随机产生值中的最小值.

3.2.3 改进的适应度函数

在完成种群初始化和免疫识别后, 程序将计算每一条染色体的适应度函数值.由于目标函数是结构造价的最小值, 故基础隔震混凝土框架结构优化问题是在有约束的前提下寻求最小化的问题, 遵循适应度函数非负性原则, 求解时需要将最低造价的目标函数转换为求最大值的形式.传统方法通过设定一个足够大的数值减去或除以目标函数值来求解最小值问题.如果选用不合理的适应度函数, 可能会导致在算法之初就出现一批竞争力较强的超常个体.在进行染色体筛选时优胜劣汰效果过于明显, 会影响到算法的全局优化性能, 或者会导致算法过早收敛, 这是因为种群中染色体之间的差异较小, 即便使用遗传操作也很难跳出当前的局部最优解.为杜绝上述问题的发生, 优化程序在选取适应度函数时需要考虑染色体的进化过程, 即在搜索速度与搜索能力之间取得平衡, 故优化算法使用改进的乘幂适应度函数[17]:

式中: Fit 为乘幂变换后得到的新适应度函数, 是隔震结构全寿命总成本WISO的函数;Cmax为一个适当的相对较大的数;ξ为一个随进化代数增加而逐渐发生动态变化的正数;t为当前进化代数;T为遗传算法最大迭代次数; avg(WISO) 为当前种群中结构总造价的平均值;ε代表一个充分小的正数, 防止分母为零.

3.2.4 罚函数

在完成当前种群P(t) 的适应度值的计算后, 需检验如下约束条件: ①每一条染色体对应隔震方案的水平向减震系数Cβ,DBE是否小于0.4; ②罕遇地震作用下的隔震层最大水平位移Uiso,MCE是否小于允许位移Ucr; ③隔震结构整体的层间位移角θk是否小于规范限制θlim;④风荷载作用下的隔震层水平剪力设计值是否小于隔震层总屈服力.

程序使用变系数的罚函数来设置上述约束条件, 当某次方案满足各约束条件时程序会保留此条染色体, 作为备选最优方案, 通过上述方法可以有效淘汰不满足约束要求的染色体, 从而提高算法的收敛性.

3.2.5 遗传操作

完成上述步骤后, 算法将运用遗传操作生成新一代种群P(t+1), 遗传操作包括选择、交叉和变异.算法采用经典的适应比例来选择策略, 染色体对应的适应度值越大, 说明该染色体更适于生存, 因此这些染色体被选中的概率就越大, 反之则会被淘汰.交叉概率是不同染色体中局部基因进行交换的概率, 交叉概率取0.8, 变异概率是染色体中基因发生变异的概率, 变异概率取0.09.

3.3 优化流程

隔震结构优化设计流程如图4 所示, 总结基于成本-效益指标的隔震结构优化流程如下:

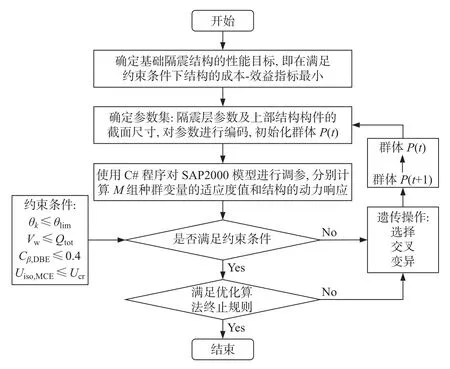
图4 优化设计流程图Fig.4 Optimization design flow chart

(1) 创建合理的数学优化模型, 确定设计变量、约束条件以及优化目标;

(2) 在结构设计软件SAP2000 中建立初始有限元模型;

(3) 优化程序中的遗传算法模块依据上述设计变量, 随机生成染色体来构建初始种群;

(4) 通过OAPI 接口调用SAP2000, 对初始模型的隔震支座和构件尺寸进行调参, 每一条染色体对应一种隔震方案, 程序会自动对隔震体系的上部结构降一度烈度设置抗震措施, 提取到构件内力后根据规范对构件进行配筋计算, 完成上述步骤以后优化程序会对免疫遗传算法中的目标函数进行抗原识别, 即对群体中的每一条染色体进行适应度函数的计算;

(5) 程序使用变系数的罚函数来设置模型约束条件, 当某次方案满足各约束条件时程序会保留此条染色体作为备选最优方案;

(6) 程序运用遗传操作对当代种群中的染色体个体进行选择、交叉和变异, 产生子代种群后, 再对子代种群的个体进行罚函数、目标函数和适应度函数的计算, 最后将子父代混合并进行选择操作, 产生下一代子代种群, 直到优化结果满足收敛精度为止.

4 算例分析

4.1 隔震模型建立

以一幢5 层基础隔震的钢筋混凝土框架结构为例, 按本工作思路进行整体性的优化设计,楼层层高为3.2 m, 建筑总高度为16 m.建筑结构的安全等级为二级, 设计使用年限为50 年,建筑抗震设防标准为重点设防类型, 设防烈度为8(0.2 g), 地震分组为第二组, 场地类别为第Ⅲ类, 场地特征周期为0.55 s, 混凝土选用C30, 钢筋选用HRB400, 钢材选用Q235 型钢, 隔震支座选型的具体布置如图5 所示.

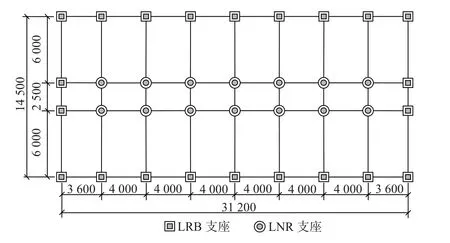
图5 隔震支座选型布置图Fig.5 Isolator arrangements of isolated building

使用SAP2000 对隔震结构进行初始建模, 其模型如图6 所示.模型的隔震层外围布置铅芯叠层支座, 内部核心区布置天然橡胶支座, 每个柱底设置一个隔震支座(共36 个).隔震层支座型号来源于优化程序中的铅芯支座库和橡胶支座库, 支座库中包含支座参数和价格, 优化时通过改变隔震支座的配比组合来实现屈服强度比as、铅芯含量η和隔震层造价的变化; 上部结构每一层的梁、柱截面尺寸都有所不同, 第k层楼层构件尺寸的长宽均不大于第k-1 层的截面尺寸, 设计变量取值的上下限如表3 所示.

图6 基础隔震结构SAP2000 模型Fig.6 SAP2000 structure model of isolated building

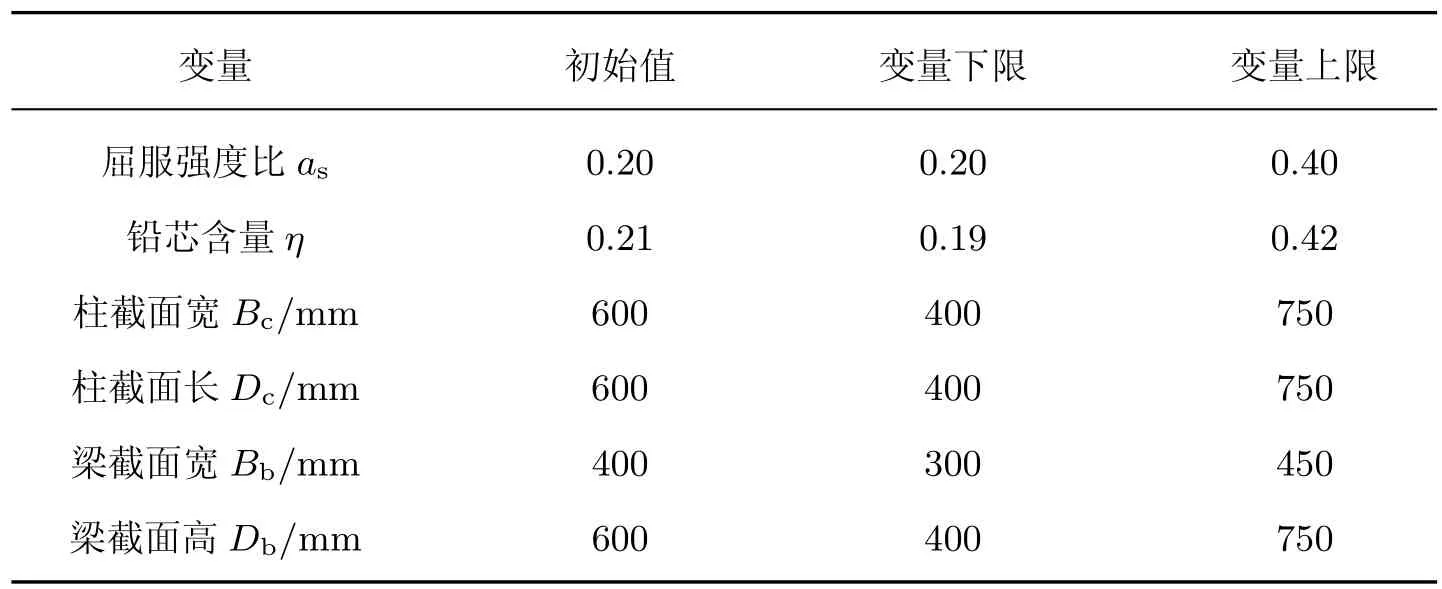
表3 设计变量上下限及初始值Table 3 Upper and lower limits of design variables and initial values

采用二进制方式对表3 中的设计变量进行编码, 算例的遗传算法参数如下: 种群数为10,交叉概率为0.8, 变异概率为0.09, 最大迭代次数为50 次, 以迭代次数作为循环的终止条件.求解任意设防烈度下结构失效概率时, 可采用基于地震动参数的易损性分析方法, 采用动力时程分析法计算隔震体系抗力值, 进而分析不同破坏等级对应的易损性矩阵, 或利用缩尺模型进行振动台试验并统计大量数据, 建立经验值来简化求解过程.为简化求解过程, 本工作采用谢礼立等[18]的经验数据来求解损伤费用, 8 度设防下混凝土框架结构各破坏等级对应的失效概率如表4 所示.

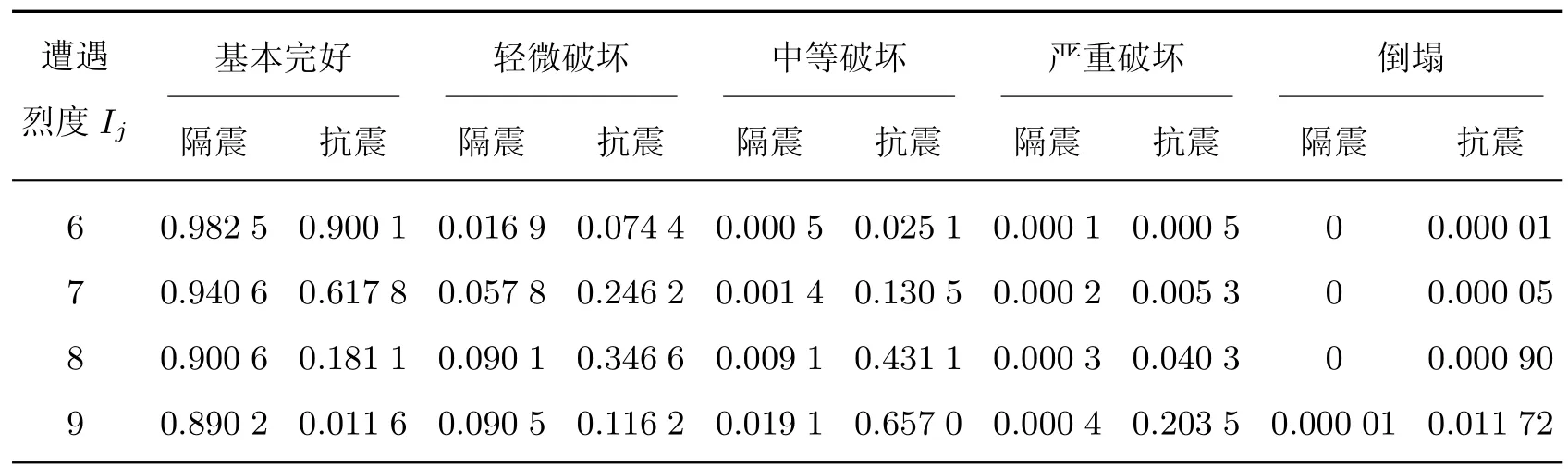
表4 隔震与抗震结构的条件失效概率Table 4 Conditional failure probability of isolated building and fixed base building

4.2 优化结果

表5 为优化后的结构梁、柱截面尺寸, 梁截面尺寸各层一致, 情况如下:x向框架梁250 mm×600 mm、y向框架梁300 mm×650 mm.隔震层支座布置情况如下: 角柱底端放置LRB350 型支座、x边柱底端放置LRB400 型支座、y边柱底端放置LRB350 型支座、中部核心区放置LNR400 型支座.隔震层参数如下: 屈服强度比as为0.246, 铅芯含量η为0.278.

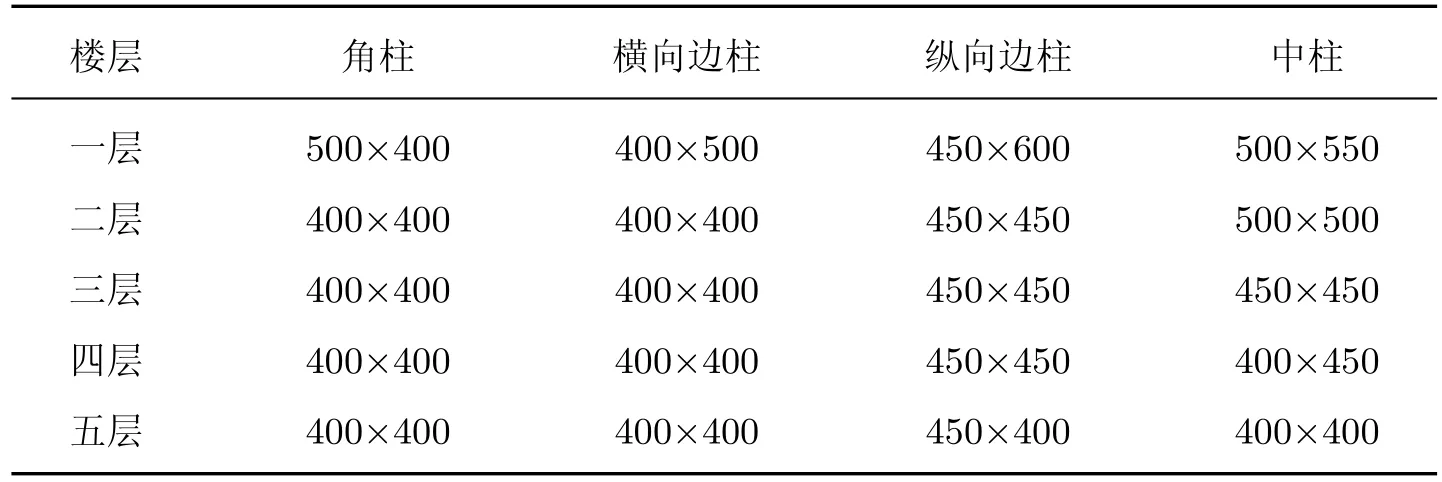
表5 设计变量的优化值Table 5 Optimal values of design variables mm

在优化计算过程中, 目标函数值µiso/non的遗传迭代过程如图7 所示.图中, 目标函数值呈现整体下降并趋于平稳的趋势, 最终µiso/non稳定在0.815 左右, 优化结果验证了优化模型及算法的正确性.优化后结构的总造价为1 429 088.36 元, 结构在生命周期内的各项总费用列于表6.

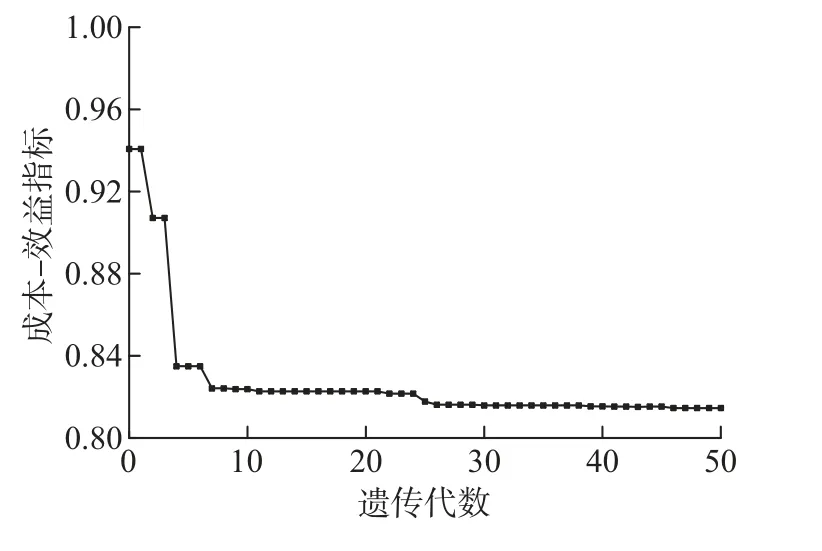
图7 µiso/non 遗传迭代示意图Fig.7 Iteration diagram of µiso/non

表6 结构各项费用优化值Table 6 Optimized values of various expenses of structure 元

4.3 时程分析法的补充验算

本工作选用2 条天然地震波和一条按抗震规范反应谱合成的人工波, 对优化后的结构进行设防烈度和罕遇烈度下的补充验算, 地震加速度分别调整至200 和400 cm/s2, 地震动输入的平均拟加速度反应谱应与规范反应谱相符合.时程分析法求得隔震结构的水平向减震系数为0.23, 地震影响系数最大值为0.046, 满足地震烈度降低一度设计的要求(见表7), 且总水平地震作用高于结构在6 度设防时的总水平地震作用, 罕遇地震下隔震支座的最大水平位移值均小于其允许极限位移值min(0.55D, 3Tr) (见表8), 满足《抗规》要求.

表7 隔震层以上结构水平地震影响系数最大值Table 7 Maximum value of the horizontal seismic influence coefficient

表8 罕遇地震下隔震支座最大水平位移Table 8 Maximum displacement of isolator under maximum considered earthquake mm

抗震结构与优化之后的隔震结构在各波形下x、y方向的最大层间位移角见表9 和10 所示.图中2 种结构在设防烈度下的层间位移角均小于1/550, 在罕遇烈度下2 种结构的弹塑性层间位移角也均小于1/50, 满足《抗规》的要求, 验证了优化模型及优化算法的正确性.

表9 设防烈度下的最大层间位移角Table 9 Maximum interlayer displacement angle under design-based earthquake

表10 罕遇烈度下的最大层间位移角Table 10 Maximum interlayer displacement angle under maximum considered earthquake

图8 显示了罕遇地震作用下上下部结构的最大层间位移角情况.从图8 中可以直观地看出: 在罕遇地震作用下, 2 种结构都能满足《抗规》中弹塑性层间位移角小于2% 的限值要求,但优化后隔震结构的上部结构最大弹塑性层间位移角与传统抗震结构相比要小很多, 减幅达到100%, 这表明基础隔震结构在罕遇地震作用下也具有良好的抗震性能.

5 结 论

(1) 本工作打破了基础隔震结构分部设计的固有思维, 采用了基于性能的基础隔震结构整体性优化设计方法.在确保隔震层性能满足设计要求的前提下, 按降低一度设计的方法对上部结构进行内力及配筋计算.最终优化后的屈服强度比as为0.246, 铅芯含量η为0.278.

(2) 通过免疫遗传算法对隔震结构进行优化后, 隔震结构工程整体的成本-效益指标明显优于传统抗震结构的设计方法, 最终目标函数值µiso/non稳定在0.815 左右.研究结果表明,采用成本-效益指标为目标函数的基础隔震结构支座参数及构件尺寸优化方法, 可直观且定量地确定建筑物的抗震性能, 在确保上部结构降低一度计算与人员安全的同时, 实现工程经济效益最大化.

(3) 优化后的基础隔震结构即使在罕遇地震作用下也具有良好的抗震性能, 与传统抗震结构的地震响应相比, 隔震结构在地震作用下可能遭受的损失将较大减少.因此, 预计在使用寿命50 年内, 隔震结构比传统抗震结构的全寿命费用低很多, 具有长远的安全性与经济性.