考虑仿真步长延时的MMC高频阻抗模型

伍双喜, 闫斌杰, 杨银国, 满九方, 刘 洋, 姚增慧, 谢小荣

(1.广东电网有限责任公司电力调度控制中心, 广东 广州 510600; 2.中国华能集团有限公司, 北京 100031; 3.清华大学电机工程与应用电子技术系, 北京 100084)

1 引言

基于我国可再生能源集约化开发与能源消费的逆向分布特征,柔性直流输电凭借其在大容量、远距离输电方面的稳定性和经济性优势已成为我国跨区输电的主要选择[1]。近年来,在包含模块化多电平换流器(Modular Multilevel Converter,MMC)的柔性直流输电系统中,高频振荡事件频发[2,3]。柔直系统高频振荡可能导致保护动作造成停电事故,进而引发大范围潮流转移,威胁电力系统的安全稳定运行,已经成为制约我国可再生能源发展的不利因素[4]。

为探究柔直系统高频振荡的产生机理,迫切需要建立分析适用的阻抗模型[5,6],其中模块化多电平换流器的准确建模是关键[7]。模块化多电平换流器内部控制环节复杂多样,通常包括锁相环、派克变换、外环控制、正序和负序电流内环控制、派克反变换和调制环节。此外,相比于传统的两电平或三电平换流器,受应用场景的限制,MMC设置了更长的控制链路延时。研究表明该延时对高频阻抗特性的影响不可忽视[8]。

由于交流信号不具备传统小信号模型线性化所需的直流工作点,因此早期的阻抗建模工作大多建立在dq坐标系下[9]。但是,dq坐标系下的阻抗模型在三相不平衡系统中交流时变,难以线性化;此外,dq坐标系下的阻抗模型没有明确的物理意义,且无法直接测量得到,难以验证理论推导结果的正确性。考虑到上述限制因素,后续研究大多采用谐波线性化方法建立abc坐标系下的小信号阻抗模型。文献[10]考虑了锁相环动态响应, 建立了abc坐标系下换流器的单入单出序阻抗模型。但是,换流器中不对称控制环节导致频率互补的分量间存在耦合,一维阻抗不适用于存在耦合关系的情况[11,12]。为解决此问题,文献[13,14]分别在αβ坐标系和dq坐标系下建立了由二维传递函数表示的多入多出阻抗模型。但是,该矩阵中的元素没有明确的物理意义,难以通过理论分析或时域仿真进行辅助验证。在此基础上,文献[15,16]在 abc坐标系下建立了考虑频率耦合效应的二维阻抗模型,利用非对角线元素表示两个互补频率分量之间的耦合关系。非对角线元素数值越大,耦合关系越明显。然而,无论阻抗模型的维度如何,以往的阻抗建模过程仅考虑换流器的内部控制环节,未充分考虑仿真步长的影响,无疑会为高频条件下的阻抗模型引入误差。

MMC复杂的控制结构以及频率耦合效应极大地提高了阻抗建模的难度,并且理论推导的模型正确性应能得到充分的验证[17]。鉴于实际工程验证的困难性,目前大多采用基于时域仿真的阻抗辨识方法进行验证。文献[18]利用阻抗辨识法验证了次/超同步频率范围下频率耦合阻抗模型的正确性[19,20]。然而,频率越高,仿真步长延时对阻抗辨识结果影响越大。因此在高频范围内,需要仔细考虑延时影响,避免阻抗辨识结果不准确,无法验证理论推导模型的正确性,不利于振荡事件的机理分析。

针对上述问题,本文首先介绍了采用的MMC二端口频率耦合阻抗模型,然后分析了仿真软件内部延时对MMC高频阻抗辨识的影响机理,进而提出了一种考虑仿真步长和控制延时的MMC阻抗建模方法。最后通过时域仿真进行检验,证明了所提出的建模方法在高频条件下阻抗辨识结果的正确性,适用于对实际柔直系统高频振荡问题的分析。

2 MMC频率耦合阻抗模型

2.1 MMC二端口频率耦合阻抗模型

由于坐标变换固有的频率变换机制以及锁相环等不对称控制环节,导致MMC交流侧存在频率耦合效应,如果在MMC交流侧注入一个频率为fp的小信号电压扰动Vp,则MMC不仅会在其交流电流中产生频率为fp的电流响应Ip,而且还会在其互补频率2f1-fp处产生电压、电流分量Vpc和Ipc来响应该扰动。现有的阻抗建模工作考虑频率耦合效应后,建立MMC的二端口频率耦合阻抗模型为:

(1)

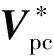
2.2 MMC二端口频率耦合阻抗模型的建立

本节采用谐波线性化方法在abc坐标系下建立MMC二端口频率耦合阻抗模型,使其在高频范围下也具有准确性[21]。

首先,基于交流端口所注入的两个频率互补的谐波扰动,推导得到控制环节生成的参考电压。在推导中,各环节输入均以时域形式表达,经理论推导得到输出结果后,再将其用频域相量表示,进而可得不同环节的传递函数。

按照上述推导原则,可将外环控制环节表示为:

(2)

同理,可推导电流内环控制的传递函数。电流内环控制中的派克变换与外环控制的派克变换基本相同,仅增加了一个标幺化环节,因此电压电流都以标幺值表示。电流内环控制包括PI环节、解耦环节以及电压前馈环节。根据其控制结构,可将电流内环控制环节表示为:

(3)

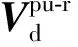
根据式(3)可知,电流内环控制生成的dq轴参考电压与dq轴电压和电流分量以及外环控制生成的dq轴参考电流有关。此外,根据派克变换,dq轴电压和电流分量可分别表示为:

(4)

(5)

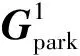
联立式(3)～式(5),换流器生成的三相参考电压标幺值可表示为:

(6)

(7)

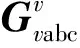
随后,推导MMC输出电压与谐波扰动之间的传递函数矩阵,即差模回路公式的传递函数矩阵。MMC的单相拓扑结构如图1所示,Lg为电网侧等效电感,Rg为电网侧等效电阻,每个桥臂含有N个子模块,L0为桥臂电感,R0为桥臂等效电阻。

图1 MMC单相拓扑结构Fig.1 Single phase topology of MMC

根据图1可得MMC差模回路公式为:

(8)

由于谐波扰动在换流器变压器网侧注入,为推导MMC的阻抗模型,需建立换流变压器网侧和阀侧的关系。由此,可建立两个互补频率下MMC的差模回路公式为:

(9)

Z=T-1A

(10)

同理可得柔直换流器频率耦合导纳模型为:

Y=A-1T

(11)

3 仿真步长延时对MMC高频阻抗辨识的影响机理分析

目前常用的电磁暂态仿真软件大多采用数值积分方法,设定的仿真步长将会影响MMC模型中各个控制环节的输入和输出结果,进而影响整个MMC阻抗模型的辨识结果。本节以PSCAD仿真软件中的锁相环控制环节为例,分析仿真步长的影响。锁相环的控制结构如图2所示,首先通过派克变换将网侧三相电压变换到dq坐标系下。然后,将派克变换得到的q轴电压分量经PI控制环节、低通滤波环节和积分环节得到相角,并将该相角反馈给派克变换环节,直至达到一个稳定状态,即可锁定网侧电压的相角θPLL。此时,派克变换输出的q轴电压应接近于零。

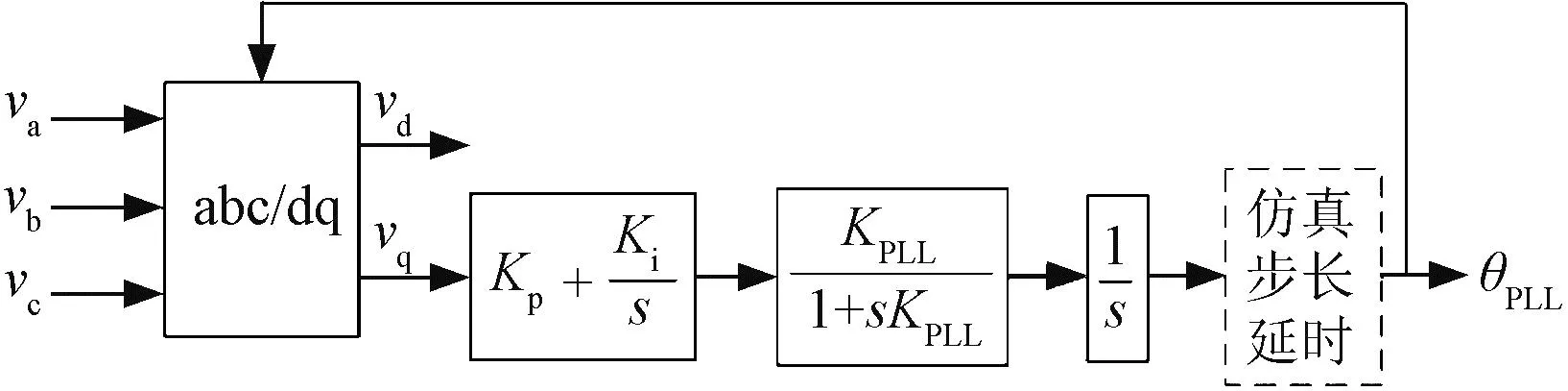
图2 锁相环控制结构图Fig.2 PLL control structure diagram

在换流器控制中,锁相环锁定的相角将用于后续外环控制和电流内环控制的派克变换中。为研究仿真步长对后续环节的影响,对比了以下两种情况:一种是设置锁相环为前序环节,使用锁相环输出相角对网侧电压进行派克变换,派克变换使用的相角经历了仿真延时环节;另一种是不设置前序锁相环环节,直接使用未经仿真延时的相角对网侧电压进行派克变换。使用的锁相环模型参数见表1,表1中,TPLL为锁相环低通滤波环节截止频率的倒数。二者时域仿真的对比结果如图3所示。如果忽略仿真步长延时的影响,两种情况下派克变换环节的输入电压和相角相同,所得到的d轴和q轴电压分量应该一致。

表1 锁相环控制参数Tab.1 Control parameters of PLL

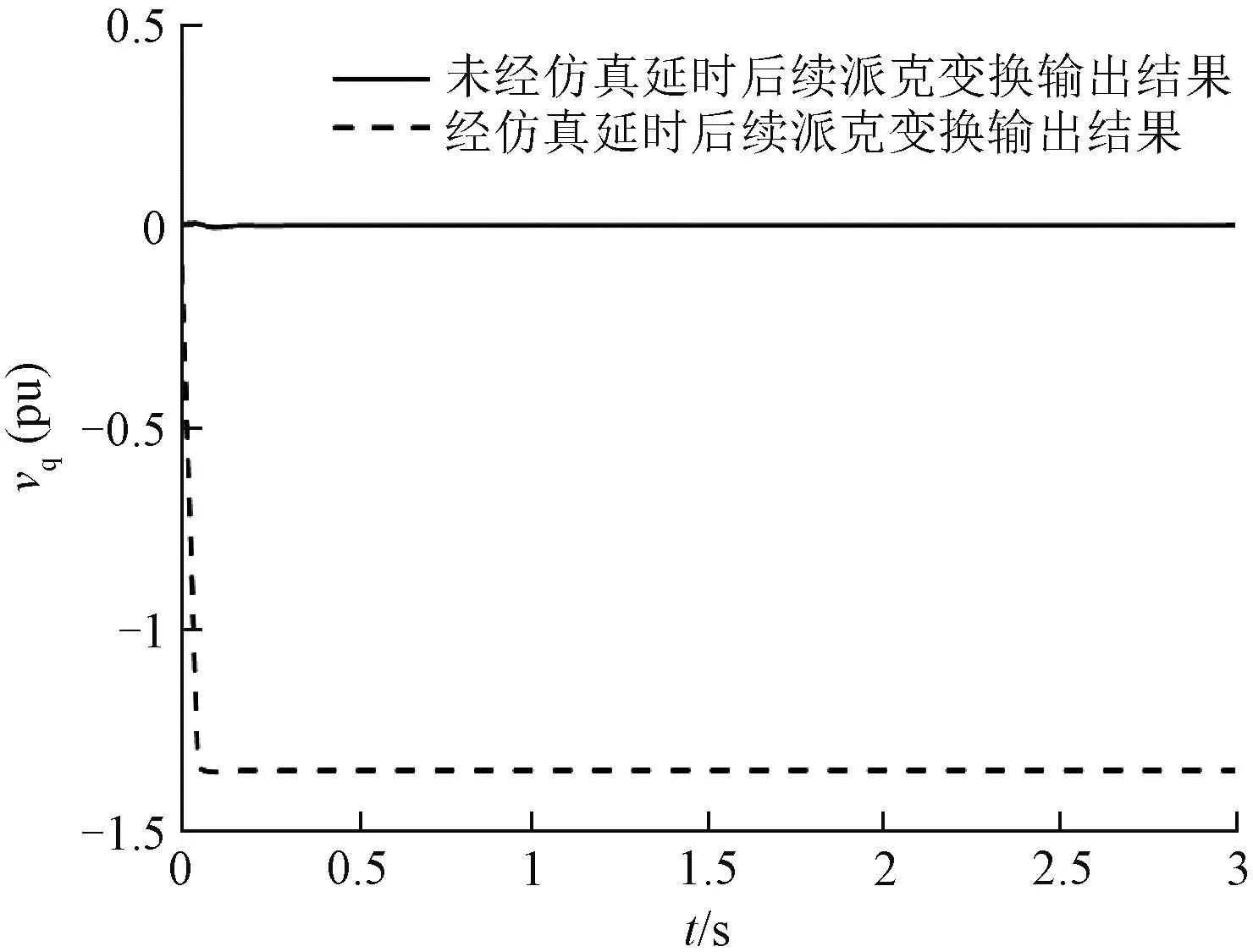
图3 q轴电压分量的对比Fig.3 Comparison of q-axis voltage components

根据图3所示结果,两种情况下派克变换输出的q轴电压分量稳定后存在明显差异,说明仿真步长延时将会影响后续环节的输入输出。而每种情况下q轴电压分量在稳定前都经历了一个时长约为0.1 s的过渡阶段,这是由于软件内部采用离散化算法所致,不会直接输出稳定结果。如果将锁相环输出的相角超前一个仿真步长,再代入后续网侧电压的派克变换,即可得到与时域仿真中相同的输出结果。因此,在理论推导中,如果某个环节的输入与前序环节有关,该环节的输入应超前一个仿真步长以保证与时域仿真结果的一致性。

根据图2所示的锁相环控制结构,采用谐波线性化方法建立锁相环的传递函数。考虑两个频率互补的谐波分量后,q轴电压中谐波分量可表示为:

(12)

式中,V1为电压基波分量幅值;ω1为基波角频率;ωp为扰动角频率;Vp为角频率ωp处电压分量幅值;φp为角频率ωp处的电压分量初相角;ωpc为扰动角频率的互补角频率;Vpc为角频率ωpc处的电压分量幅值;φpc为角频率ωpc处的电压分量初相角;θPLL为派克变换使用的锁相环相角。

由式(12)可知,谐波电压扰动将在q轴电压中产生频率为fp-f1的谐波分量。根据锁相环控制结构,该谐波分量将产生同频的相角扰动。锁相环的输出相角可表示为:

θPLL(t)=ω1t+Δθ(t)

(13)

Δθ(t)=AΔθcos(ωpt-ω1t+φΔθ)

(14)

式中,AΔθ为角频率ωp-ω1处的电压分量幅值;φΔθ为角频率ωp-ω1处的电压分量初相角。

将式(13)代入式(12),并忽略二阶及以上阶数的谐波分量后可得:

(15)

在频域下,可将式(15)表示为:

(16)

锁相环内部的PI控制环节、低通滤波器环节、积分环节的传递函数为:

(17)

q轴电压与锁相环输出相角之间的关系为:

Δθ=HPLL(sp-s1)ΔVq

(18)

式中,HPLL(sp-s1)为锁相环输出相角与q轴电压的传递函数。

将式(16)代入式(18),可推导得:

(19)

式中,闭环传递函数为:

(20)

尽管上述推导考虑了时域仿真中锁相环的各个环节,理论推导和时域仿真的结果仍存在较为明显的差异。考虑到仿真步长延时的影响,在锁相环输出中附加一个仿真步长延时环节,如图2所示。此时,锁相环输出相角的理论推导结果与时域仿真结果在宽频范围下可保持一致。进一步推广,为了与时域仿真结果对应,在理论推导中,每个控制环节的输出均应延时一个仿真步长。

根据本节的分析结果,仿真软件内部的仿真步长延时对控制环节的输入输出结果会产生较大影响。为了与时域仿真结果对应,在对相关环节进行建模时,每个控制环节的输出均应延时一个仿真步长,而输入则取决于与前序环节的关联性。

4 考虑仿真步长和控制延时的MMC模型

4.1 考虑仿真步长对控制环节的修正

由上述分析可知,在时域仿真中仿真步长延时将影响各个环节的输入和输出。如果在阻抗建模时忽略仿真步长的影响,理论推导结果和时域仿真中的阻抗辨识结果难以在高频范围下保持一致,无法相互验证各自的准确性。因此,在阻抗建模过程中考虑仿真步长延时对于各个环节输入和输出的影响十分必要。根据各环节输入量是否与前序环节的输出有关,仿真步长延时可分为两种情况考虑:

(1)输入量与前序环节输出无关

当某控制环节的输入量与前序环节无关时,该环节的输入量无需考虑仿真步长的影响。该环节的输出量需延时一个仿真步长,等效仿真软件内部计算延时。

(2)输入量与前序环节输出有关

当某控制环节的输入量与前序环节有关时,该环节的输入量需超前一个仿真步长来补偿前序环节的内部计算延时,保证时域仿真中各环节的计算能够在同一时刻进行;输出量则需延时一个仿真步长,等效仿真软件内部计算延时。

需要注意的是,对于线性环节且输入量与输出量的频率完全相同时,输入量的超前和输出量的滞后可以相互抵消,无需考虑仿真步长的影响,如PI控制等环节。

4.2 考虑仿真步长的MMC频率耦合阻抗模型

采用谐波线性化方法在abc坐标系下建立考虑仿真步长和控制延时的MMC频率耦合阻抗模型。首先,基于交流端口所注入的两个频率互补的谐波扰动,推导得到控制环节生成的参考电压。随后,根据MMC差模电压回路建立MMC输出电压与外部注入谐波扰动之间的关系。最后,将上述结果联立,建立MMC的频率耦合阻抗模型。建模方法流程如图4所示,具体步骤如下:

图4 阻抗建模方法流程图Fig.4 Flow chart of impedance modeling method

步骤1:收集目标柔直系统的换流器电气参数,通常包括换流变压器参数、桥臂电阻、桥臂电抗等。

步骤2:收集目标柔直系统的换流器控制参数,包括锁相环控制参数、外环控制参数、电流内环控制参数、调制比和控制链路延时等。

称取10 g经预处理的丝瓜络纤维，在室温下平衡24 h后称重，然后置于50℃的烘箱中，纤维开始放湿，每5 min称量一次，当前后两次重量之差小于5%时，则已达到平衡。此时的重量为干燥重量，计算回潮率，结果见表1。

步骤3:推导控制环节传递函数。按照MMC各个控制环节的建模过程进行推导。需要注意的是,在推导过程中需考虑仿真步长的影响,对输入和输出进行修正。例如,在锁相环推导中,进一步考虑仿真步长影响,加入延时环节,可将锁相环开环传递函数修正为:

(21)

式中,Td为锁相环延时的时间常数。

修正后得到的锁相环输出相角与时域仿真结果完全一致。

步骤4:推导MMC输出电压与谐波扰动之间的传递函数矩阵,即差模回路公式的传递函数矩阵。

步骤5:将上述结果联立,构建MMC的频率耦合阻抗模型,如式(10)所示。

5 仿真验证

为验证前述所提出的考虑仿真步长延时的MMC频率耦合阻抗模型理论推导结果的正确性,本节在电磁暂态仿真平台进行MMC的阻抗辨识,仿真步长设为10 μs。

以典型的柔性直流输电系统拓扑为例,如图5所示,在PSCAD/EMTDC电磁仿真平台中搭建了单端换流器的非线性仿真模型,两侧分别接入理想的交流电网和直流电网。MMC具体拓扑结构如图6所示。其中,换流器额定容量为1 000 MW,直流电压等级为±350 kV,桥臂电感为105 mH;换流变压器采用单相双绕组变压器组,额定容量为3×375 MW,变压器变比为525 kV/375 kV,漏抗为0.14 pu;换流器详细参数见表2。

表2 换流器参数Tab.2 Parameters of MMC

图5 单端柔性直流输电系统仿真结构Fig.5 Simulation structure of single-ended flexible MMC-HVDC transmission system

图6 MMC仿真拓扑Fig.6 MMC simulation topology

图7 MMC控制结构框图Fig.7 MMC control structure block diagram

分别在考虑仿真步长延时和不考虑仿真步长延时两种情况下,通过理论推导得到了换流器的频率耦合阻抗模型,二者与时域仿真中的阻抗辨识结果在高频(1 000～2 000 Hz)范围内的对应结果如图8所示。图8中,R表示实部,I表示虚部。

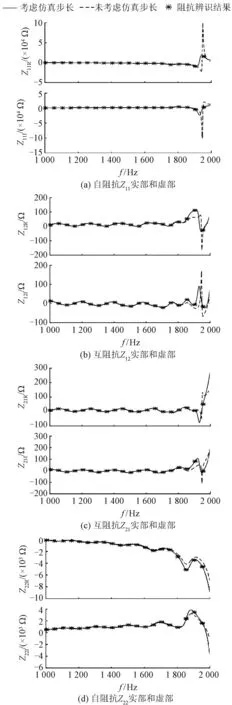
图8 两种情况下理论推导和阻抗辨识结果的对比Fig.8 Comparison between theoretical derivation and impedance identification

图8结果显示,仿真步长延时将影响换流器在高频下的阻抗特性。考虑仿真步长延时后,换流器频率耦合阻抗模型的理论推导结果与时域仿真中的阻抗辨识结果在高频范围下仍保持高度一致。若不考虑仿真步长,理论推导结果与时域仿真中的阻抗辨识结果在高频范围下将存在明显的误差。对比结果表明,本文所提出的考虑仿真步长延时的MMC频率耦合阻抗模型能够与阻抗辨识结果在高频下相互验证各自的准确性,具有较强的应用价值,可应用于实际柔直系统高频振荡的稳定性分析。

6 结论

针对高频范围下理论推导阻抗模型与时域仿真中的阻抗辨识结果无法相互对应的问题,提出了考虑仿真步长延时的阻抗建模方法,并建立了考虑仿真步长和控制链路延时的MMC频率耦合阻抗模型。在理论推导过程中,分析了仿真延时对MMC控制环节的输入和输出的影响并对模型进行修正。最终的仿真结果表明,考虑仿真步长和控制链路延时后的MMC模型与阻抗辨识结果在高频范围内保持一致,证明了该模型的正确性,解决了仿真步长导致的阻抗辨识的高频偏差问题,可用于柔直系统高频振荡的稳定性分析。