考虑一次调频死区的风电机组虚拟同步控制参数优化研究

2024-01-08曹俊英刘育明李登峰李小菊

电工电能新技术 2023年12期

曹俊英, 姚骏, 刘育明, 罗艺, 李登峰, 李小菊

(1.输变电装备技术全国重点实验室(重庆大学), 重庆 400044; 2.国网重庆市电力公司电力科学研究院, 重庆 401123)

1 引言

在环境污染和能源危机的压力下,新能源的开发和利用在现代电力系统中得到了越来越多的关注和快速发展[1,2]。风电机组通过电力电子变流器接入电网导致其与电网解耦从而不能提供频率支撑,因此,用风电机组代替传统的同步发电机必然会减小系统惯量,削弱系统的频率调节能力[3-6]。在受到干扰的情况下,高比例可再生能源系统更容易发生电网频率事故[7,8]。

一方面,为解决高占比可再生能源系统低惯量弱阻尼这一问题,国内外众多学者提出了虚拟同步发电机控制策略,即通过模拟同步发电机的转子特性,使逆变器具有惯量和阻尼[9,10]。在一定程度上可抑制其输出频率和功率的波动,提高系统稳定性,具有广阔的应用前景[11]。

另一方面,风电机组参与调频的方式主要通过减载控制[12-14]和转子动能控制[15,16]来实现。减载控制又分为桨距角控制和转子超速控制,使风电机组无法运行在最大功率跟踪(Maximum Power Point Tracking, MPPT)运行点上,即减少了风能捕获量,降低了风电场的经济效益,且桨距角动作频繁会增加风电机组的机械磨损程度。转子动能控制方式能使风电机组在正常运行时仍工作在最佳运行点,无需额外投资。因此,本文重点研究利用转子动能实现风电机组的频率支撑。转子动能控制中调频系数过小不利于充分发挥风电机组的调频能力,调频系数过大易导致机组转速超过约束值。因此,国内外学者对风电机组转子动能控制中一次调频系数的选取展开了研究。文献[17-19]采用固定一次调频系数控制,新能源机组适应性较差,在不同风速工况下新能源机组的频率响应能力具有一定的局限性。为此,文献[20]通过适应不同风速工况制定变下垂系数控制方法,但风机处于减载状态,未运行在最优工作点,降低了风电场的经济性。文献[21]通过模型预测控制,对风机桨距角和储能功率进行优化分配,首先该策略的执行过程较为复杂,其次桨距角频繁动作会缩短风电机组使用寿命,且引入储能将增加风电场投入成本。文献[22]考虑风机转子动能限制及系统频率二次跌落,通过优化得到风电机组最优功率曲线,然而该方法并未综合考虑变流器容量是否超过限制。文献[23]利用模糊控制与预测控制相结合的联合控制方法提升虚拟同步发电机(Virtual Synchronous Generator,VSG)参与系统频率响应支撑性能,但该方法假设该逆变器具有无限大储能,并未将该控制策略应用于有限调频能力的风电机组中,实际工程应用价值有限。文献[24]研究了一种自适应惯量阻尼综合控制策略,提出了VSG虚拟转动惯量系数与虚拟阻尼系数的交错控制策略,但未说明惯量与阻尼系数的参数制定原则。文献[25]综合考虑基于VSG控制的风电机组与储能系统的一次调频特性,提出一种风储协调调频控制策略。综上所述,在已有研究中,缺少深入挖掘VSG控制中实际能量来源的频率调节能力。其次,未有对于风电机组转子转速约束与变流器容量限值综合考虑后的参数制定原则。且上述文献均未定量考虑风电机组一次调频死区对风电机组参与调频过程中的影响,有研究表明如果不计及一次调频死区的影响,分析所得频率偏差小于实际值,将不能全面评估风电机组频率调节能力[26]。因此,在进行风电机组调频参数优化研究时,应更精细化考虑一次调频死区的建模,以此准确地表征风电机组一次调频能力,提高新型电力系统应付负荷突变的能力以及系统的频率稳定性。

针对上述问题,本文首先在采用VSG控制的风电机组模型基础上计及一次调频死区的影响,从系统频率响应的量化解析表达式入手,通过时域解析推导了系统发生负荷扰动后系统频率响应全过程的评估指标表达式;进而从轨迹灵敏度分析的角度出发研究风电机组调频参数与频率响应的关联程度,选取起关键作用的虚拟阻尼系数进行参数整定;进一步考虑转子转速约束及变流器容量限值得出调频物理约束边界下虚拟阻尼系数优化值;基于此,本文提出了一种考虑一次调频死区及调频物理约束边界的风电机组虚拟同步控制参数优化方法,最后通过Matlab/Simulink仿真表明所提策略的有效性。

2 基于VSG控制的风电机组调频控制

2.1 VSG控制

风电机组由于采用变流器控制使得机组转速与系统频率完全解耦,无法提供频率支撑。实际运行过程中可通过模拟同步发电机特性来改进风电机组控制技术,从而使风电机组为电网提供惯量和阻尼,图1为VSG控制框图。

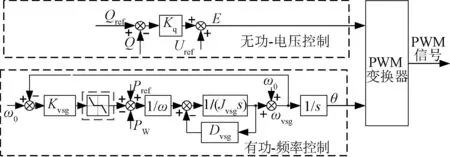
图1 VSG控制框图Fig.1 VSG control block diagram

VSG控制策略主要包括有功-频率控制和无功-电压控制。VSG的有功-频率控制方程式如下所示:

Dvsg(ωvsg-ω0)

(1)

式中,Pref为有功参考值;PW为输出有功功率;Kvsg为一次调频系数;ω0为额定角频率值;ωvsg为VSG输出角频率;Jvsg为VSG虚拟惯量;Dvsg为VSG虚拟阻尼。

VSG的无功-电压控制方程如下所示:

E=Kq(Qref-Q)+Uref

(2)

式中,Qref为系统无功功率参考值;Q为VSG控制输出无功功率;Uref为逆变器输出电压幅值给定值;Kq为无功-电压下垂调制系数。将该VSG控制应用于风电机组进行频率调节,提升系统频率稳定性。

2.2 基于VSG控制的风电机组调频控制模型

VSG控制的风电机组模型包括风力机模型、轴系转动模型、最大功率跟踪控制和VSG控制系统。设风力发电机(Wind Turbine Generator,WTG)工作在最大功率跟踪模式,只能利用转子动能对系统频率提供支撑。基于VSG控制的风电机组调频控制框图如图2所示。

图2 风电机组控制框图Fig.2 Control block diagram of WTG

当风电机组运行在MPPT模式,即采用最大功率跟踪控制,此时风电机组输出功率仅由WTG转子转速决定,此时MPPT输出功率可表示为:

(3)

式中,kω为最大功率跟踪系数;ωr为风机转子转速。

由于本文需量化推导出系统的频率响应表达式,因此采取最小二乘法对MPPT控制环节输出功率进行线性化处理,将该环节解析为传递函数表达。风机转子转速最小约束值为0.7 pu,最小二乘法拟合过程如图3所示。

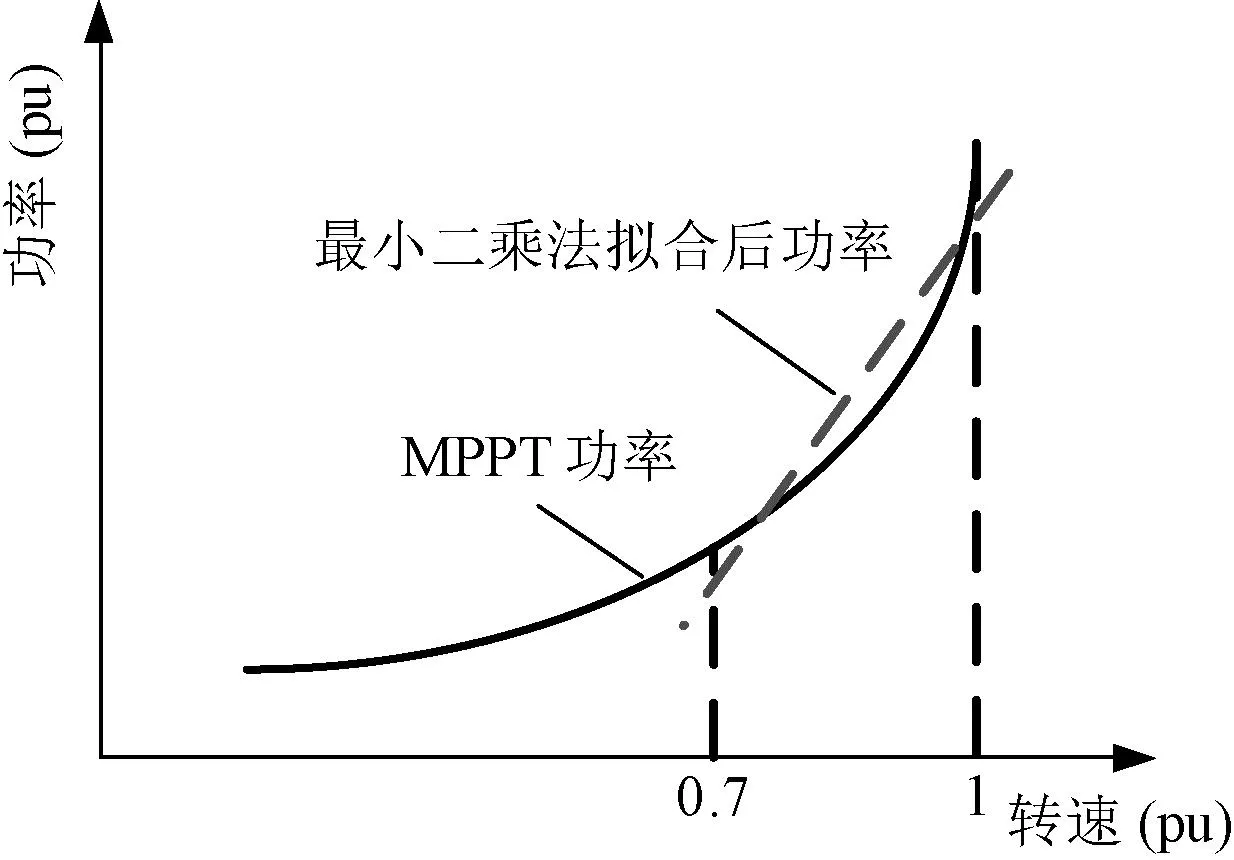
图3 最小二乘法拟合过程Fig.3 Least square fitting process

通过最小二乘法线性化后MPPT输出参考功率为:

PMPPT=kωr-b

(4)

式中,k、b为经过最小二乘法线性拟合后直线的斜率与截距。

风机输出电磁功率可表示为:

PWTGe=PMPPT+ΔPd

(5)

式中,PWTGe为风力机输出电磁功率;ΔPd为风机附加调频控制模块输出的电磁功率修正量。

风电机组转子运动方程为:

(6)

式中,HWTG为风力机惯性时间常数;PWTGm为风力机捕获功率。

在风机参与系统调频过程中,风机转子转速将发生变化,而在这一时间尺度下,可认为风速不变。为简化分析,可忽略PWTGm的变化,假定风机的机械出力等同于风机在MPPT控制下的输出功率。因此,在风机参与调频过程中,式(6)的小信号方程可表示为:

(7)

式中,ωr0为风机调频前初始转子转速;ΔPWTGe为风机输出功率变化量;Δωr为风机转子转速变化量。

联立式(4)、式(5)将其代入式(7)有:

(8)

3 电网频率响应分析

为推导整个系统的频率响应解析表达式,本文假定该系统具有统一频率,任何节点或发电机的频率动态都是相同的。所分析系统拓扑图如图4所示,包括一个同步发电机、一个风力发电机、一个负载,通过时域解析来推导该系统频率响应表达式。

在对系统频率响应建模过程中,通过加入风电机组调频控制,对经典频率响应模型进行修正,系统频率响应控制框图如图5所示。

图5 系统频率响应控制框图Fig.5 System frequency response control block diagram

假设t0时刻前系统处于正常运行状态,常规同步发电机、风力发电机、负载功率处于平衡状态。在t=t0时,系统负载在原有PL0基础上增加ΔPL,系统频率降低。传统的同步发电机和风电机组检测到频率偏差后共同参与一次调频,整个系统的发电机转子运动方程如式(9)所示。

(9)

式中,H为系统等效惯性时间常数;DL为系统负荷阻尼系数;ΔPSG为常规同步发电机的输出功率变化量;ΔPW为风力发电机的输出功率变化量。

对于常规同步发电机,功率增量ΔPSG与频率偏差Δf成正比,同步发电机一次调频动作可简化为一阶惯性环节。因此,常规同步发电机的功率方程为:

(10)

式中,TG为汽轮机再热时间常数;KG为常规同步发电机一次调频系数。

对于VSG控制的风力发电机,功率变化ΔPW与频率偏差和频率变化率有关,风机输出功率变化ΔPW表达式如下所示:

(11)

式(11)中,ΔPref=ΔPMPPT,VSG控制的有功功率参考值即风力机MPPT输出功率。通过VSG控制,风机在参与调频控制过程中附加的电磁功率增量如下所示:

(12)

将式(12)代入式(8)可得风机参与调频过程中转子转速偏差表达式为:

(13)

将式(13)代入式(11)可得风机输出功率变化量表达式为:

(14)

在实际电力系统中,风电机组一次调频死区的设置至关重要,可避免频率小范围扰动时机组频繁动作而降低设备寿命。为进一步直观分析风电机组一次调频死区大小d对系统频率响应的影响,按照表1的仿真参数,绘制不同调频死区大小系统的频率响应曲线,如图6所示。

表1 仿真参数Tab.1 Simulation parameters

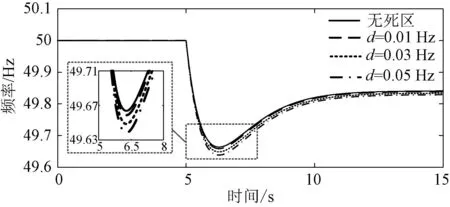
图6 系统频率响应曲线Fig.6 System frequency response curve

根据图6可知,与考虑风电机组一次调频死区作用的结果相比,无一次调频死区的系统频率响应特性更优,且死区设置越大,系统频率响应最低值越小。

据此,如果在进行系统频率响应分析时不考虑一次调频死区的影响,则频率偏差分析结果将小于电网实际频差,这会影响风电机组频率调节能力的准确估计,不能充分挖掘风电机组一次调频能力,不利于新型电力系统协调稳定运行。因此,量化分析一次调频死区带来的影响,全面评价风电机组频率调节能力、对指导提高新型电力系统负荷应变的能力、提高新能源消纳具有积极的意义。

含一次调频死区的风力发电机组在参与系统频率调整时,首先将系统频率偏差与死区大小进行比较,若频差小于等于死区时,风电机组不参与系统一次调频;反之当频率偏差大于死区时,风电机组有功-频率下垂附加控制发挥作用。因此,含死区的一次调频功率表达式如下所示:

(15)

式中,ΔPf为一次调频输出功率;d为死区幅值;Δf=fvsg-f0,fvsg为风机输出频率,f0为电网频率。

设负荷突增使频率跌落大于死区,当考虑一次调频死区的量化与建模后,其一次调频功率表达式较不考虑死区相比附加一个常数量表达式-Kvsgd,此常数量表达式可作为扰动量加在传递函数框图中,此扰动量与负荷扰动量在框图中位置一致,含一次调频死区的系统频率响应控制框图可认为在输入的负荷扰动量上叠加死区常数量。综上,可得VSG控制的风电机组参与调频的电网频率响应模型如图7所示。

图7 风机参与调频的频率响应模型Fig.7 Frequency response model

在图7传递函数框图分析的基础上,当频率响应受到阶跃功率扰动ΔPL,令DP=Dvsg+Kvsg,该系统输出Δf(s)的表达式如式(16)所示。

(16)

式中

p0=2HWTGωr0TG

p1=TGk+2HWTGωr0

p2=k

q0=4HWTGHωr0TG+2JvsgTGHWTGωr0

q1=2JvsgHWTGωr0+2TGHWTGωr0DP+2HTGk+

4HWTGHωr0+2TGHWTGωr0DL

q2=2KGHWTGωr0+2HWTGωr0DP+2Hk+TGkDL+

2HWTGωr0DL

q3=KGk+DLk

将式(16)整理后进行拉普拉斯逆变换可得时域表达式为:

(m0+m1eλt+C1eλ1t+C2eλ2f)

(17)

式中,m0、m1、C1、C2、λ、λ1、λ2为系统频率响应的时域表达系数。

由式(17)可求得最大频率偏差Δfmax与最大频率变化率,如下式所示:

(18)

式中,t1为频率最低点所对应时间。式(17)和式(18)分别表征了考虑一次调频死区后系统频率变化的时域特性及关键指标,该解析表达将为后文进一步优化频率调节参数奠定量化基础。

4 轨迹灵敏度分析

(19)

式中,Δxi为第i个参数的变化量;m为待分析的参数个数。

较大轨迹灵敏度所对应的调频参数对频率响应具有较强的动态轨迹影响,即当该值发生微小变化时,频率响应的动态轨迹会发生较大改变;反之,较小轨迹灵敏度所对应的调频参数发生微小变化不会对频率响应的动态轨迹有明显地改变。将调频参数Jvsg、Dvsg、Kvsg及d的轨迹灵敏度进行仿真计算分析后,得出各参数发生变化对频率响应全过程的动态轨迹影响的强弱程度,如图8所示。分析结果表明虚拟阻尼系数Dvsg对频率响应具有较强的动态轨迹影响,在调频过程中起关键作用。

图8 轨迹灵敏度曲线Fig.8 Trajectory sensitivity curve

由于实际系统通常为离散系统,所采集的观测量为离散量,而式(19)主要用于计算连续观测量的轨迹灵敏度,将式(19)离散化可得到离散观测量的平均灵敏度计算公式如式(20)所示。

(20)

式中,L为数据总长度。

由式(20)计算得到的离散灵敏度大小见表2,该表可定量表示灵敏度大小。根据表2可知,虚拟阻尼系数Dvsg离散灵敏度最大,此结果与轨迹灵敏度曲线分析结果一致。

表2 轨迹灵敏度大小Tab.2 Trajectory sensitivity

由此,选取与系统频率响应关联程度最大的虚拟阻尼参数进行设计,更具有针对性地来提高频率响应动态性能。

5 风电机组调频物理约束边界的虚拟阻尼参数优化研究

由第4节分析可知,选取虚拟阻尼系数进行参数优化设计,由于虚拟阻尼系数的大小直接影响到风电机组参与系统的一次调频出力,在不同的风速条件下风电机组的实时可用调频容量不同,如果采用固定的虚拟阻尼参数不利于调频效果。

基于此,为使风电机组充分利用旋转动能响应系统频率变化,本节根据不同运行工况及调频物理约束边界条件,量化风电机组频率调节能力,进而推导出虚拟阻尼系数范围。从以下两方面来分析不同风速工况下风电机组的调频物理约束条件,一是转子转速约束,二是变流器容量限值。

首先考虑转子转速约束下的虚拟阻尼系数范围,最低转速应大于最低值(0.7 pu)。

Δωr≤ωr0-0.7

(21)

联立式(13)、式(21)可得考虑转子转速约束的虚拟阻尼系数取值上限如下所示:

(22)

式中,Δωr.max为转速最大变化量;dωr/dt为转速变化率;Δfmax及dΔf/dt可通过式(18)计算得到,其余系统参数均为已知值。因dωr/dt不断变化,为满足变化过程中式(22)不等号始终成立,dωr/dt应取最小值。在ωr由初始值变化为最小允许值的过程中,当ωr处于最低点时,dωr/dt最小,此时取值为0。由此,将dωr/dt的最小值代入式(22)即可求出满足转子转速约束的虚拟阻尼系数取值上限。

在频率响应过程中,调频物理约束范围内虚拟阻尼系数越大,风电机组所能提供的转子动能支撑力度越大,系统频率响应性能最好。因此,根据式(22)计算出的虚拟阻尼系数取值上限即为考虑转子转速约束后的虚拟阻尼系数优化值。

其次,考虑变流器容量限值。风速越大,风电机组输出功率越接近容量限值,为保证机组的安全运行,机组调频过程中应满足风电机组输出电磁功率小于变流器容量限值Pmax,该限值大小为1.2 pu。由风电机组输出电磁功率表达式与变流器容量限值约束可求得虚拟阻尼系数取值上限如下所示:

(23)

同理,根据式(23)得出的虚拟阻尼系数取值上限即为考虑变流器容量限值约束后的虚拟阻尼系数优化值。

综上,风电机组频率调节能力的评估应综合考虑转子转速约束和变流器有功容量限制。高风速时转子动能储存量大,但调频过程中易受变流器容量限值影响。低风速时,变流器容量裕度大,但其转子转速低易降至最低允许值以下,将可能引发频率发生二次跌落问题。因此,在不同运行工况下虚拟阻尼系数的优化取值结果应同时满足转子转速约束和变流器有功容量限制约束,虚拟阻尼参数优化值Dvsg.opt为式(22)与式(23)中的较小值。

Dvsg.opt=min(Dvsg.1,Dvsg.2)

(24)

6 仿真分析

6.1 仿真系统

在Matlab/Simulink软件中搭建了如图4所示的系统仿真模型。该模型包含一台5 MW火电机组,一台2 MW永磁直驱风电机组和负荷。为分析本文所提虚拟阻尼参数优化设计方法在不同风速情况下的有效性,选取三个典型算例进行仿真分析,选取低、中、高代表风速依次为9 m/s、11 m/s、13 m/s,并将扰动方式设置为在第5 s时系统突增负荷,一次调频死区按0.03 Hz的典型值进行设置。

6.2 低风速仿真分析

算例1:风速为9 m/s,在第5 s时系统突增负荷0.2 MW。虚拟阻尼系数Dvsg分别取为2 pu、4 pu、5.53 pu,其中5.53 pu为按照本文设计方法整定的虚拟阻尼系数,仿真结果如图9所示。

图9 算例1仿真结果Fig.9 Simulation results of example 1

由图9(a)可得,在虚拟阻尼系数Dvsg分别取2 pu、4 pu、5.53 pu时,频率跌落的最低点分别为49.792 Hz、49.808 Hz、49.822 Hz。同时观察频率的跌落速度,当Dvsg为2 pu时,系统频率响应经过2.52 s到达最低点;当Dvsg为4 pu时,系统频率响应经过3.21 s到达最低点;而当Dvsg为5.53 pu时,系统频率响应经过3.92 s跌落至低点,表明当Dvsg取5.53 pu时可在频率下降期间降低频率变化率,且在频率恢复过程中,恢复速度更缓和。由图9(b)可知,当虚拟阻尼系数设置为5.53 pu时,转子转速最小值接近但不低于0.7 pu,表明所提策略可充分利用机组的转子动能,提高系统频率稳定性。

6.3 中风速仿真分析

算例2:风速为11 m/s,在第5 s时系统突增负荷0.5 MW。虚拟阻尼系数Dvsg分别取为4 pu、6 pu、8.05 pu,其中8.05 pu为按照本文策略优化的虚拟阻尼系数,仿真结果如图10所示。

图10 算例2仿真结果Fig.10 Simulation results of example 2

图10(a)中,当虚拟阻尼系数Dvsg分别取4 pu、6 pu、8.05 pu时,频率最低点分别为49.468 Hz、49.476 Hz、49.490 Hz。同时观看频率变化速度,当Dvsg取4 pu时,系统频率响应经过3.01 s到达最低点;当Dvsg为6 pu时,经过3.36 s到达最低点;而当Dvsg为8.05 pu时,经3.78 s跌落至最低点,表明当Dvsg取8.05 pu时可在频率下降时期降低频率变化率。在频率恢复过程中Dvsg取8.05 pu时变化速度也更缓和。图10(b)中,当虚拟阻尼系数设置为本文所提策略计算值时,转子转速最小值为0.74 pu,表明在中风速情况下风电机组充分利用可用调频容量,提升风电机组频率支撑性能。

6.4 高风速仿真分析

算例3:风速为13 m/s,在第5 s时系统突增负荷0.5 MW。虚拟阻尼系数Dvsg分别取6 pu、7.9 pu、9.87 pu,其中9.87 pu为按照本文所提策略设计的虚拟阻尼系数,仿真结果如图11所示。

图11 算例3仿真结果Fig.11 Simulation results of example 3

从图11(a)可以看出,在虚拟阻尼系数Dvsg分别取为6 pu、7.9 pu、9.87 pu时,频率跌落的最低点分别为49.730 Hz、49.752 Hz、49.773 Hz。同时观察频率的跌落速度,到达最低点时间几乎一致,但当Dvsg为9.87 pu时,最低点高于其他两种取值,可表明当Dvsg取9.87 pu时可在频率下降期间降低频率变化率,且在频率恢复过程中更缓和。由图11(c)可知,当虚拟阻尼系数设置为9.87 pu时,风电机组输出有功功率最大值接近1.2 pu,表明采用此控制策略可充分利用机组的转子动能同时满足变流器容量不超过其限值,由此提高风电机组频率支撑能力。