计及饱和磁化的铁磁材料EEL损耗模型研究

赵志刚, 赵安琪, 王丽美, 高鹏旭, 卢子奇

(1.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学), 天津 300132; 2.河北省电磁场与电器可靠性重点实验室(河北工业大学), 天津 300132)

1 引言

开展铁磁材料磁特性及损耗特性研究,对变压器电磁设计、结构优化和节能降耗有着十分重要的工程意义[1]。铁心损耗是变压器产品设计中的一项重要指标,其准确计算是变压器磁特性分析中最基础、最重要的环节。随着电力电子器件以及非线性设备广泛应用于直流输电系统,很多电磁装置运行于谐波激励条件[2,3]。相较于正弦激励,谐波工况下铁磁材料的磁滞回线会发生明显的畸变,有些情况甚至会出现局部磁滞回环,进而引起磁损耗的显著增加[4,5],造成变压器局部过热,影响绝缘性能,威胁到变压器的安全运行稳定性,甚至会降低变压器的使用寿命。因此提出一种高效且准确适用于谐波工况的损耗计算方法具有重要意义。

目前针对铁磁材料磁心损耗的研究方法主要包括三种:Steinmetz经验公式法、损耗分离法以及磁滞模型法。Steinmetz经验公式是关于磁化频率和磁通密度幅值的函数,公式所需要的参数可从厂商提供的数据中提取,在工程中应用最为广泛。但原始经验公式仅应用于正弦激励条件,为解决非正弦激励磁损耗的计算问题,多个改进Steinmetz经验公式如MSE、GSE、IGSE等被相继提出[6-8]。然而,经验公式法缺少对磁性材料损耗产生机理的描述及解释,缺乏一定的物理意义;且模型参数随频率变化明显,难以适应宽频下的损耗预测,因此具有相对的局限性。

损耗分离法考虑了材料磁化过程中的能量交换和物理机理,将铁磁材料磁损耗分离为磁滞损耗、涡流损耗和异常损耗分别进行计算。针对复杂非正弦服役工况,现有文献大多利用激励波形特征在损耗分离公式中引入修正系数,使改进损耗模型适用于多工况磁损耗的计算[9-11]。损耗分离模型具有一定的物理意义,在计算损耗时可以充分考虑材料的磁化特性和波形特征,普适性更好。但在计算复杂谐波工况时,损耗分离法很难直接考虑偏滞小回环对损耗的影响,使得损耗计算产生很大的误差。

磁滞特性建模法是通过建立磁通密度B与磁场强度H之间的本构关系,实现铁磁材料磁性能的有效模拟,目前经常应用的磁滞模型主要分为J-A模型、 Preisach模型、Energetic模型[12-14]。磁滞模型有其特定的物理意义,并且可以模拟铁磁材料的磁滞曲线,同时计算磁损耗,具有良好的有效模拟性和工程实用性。但磁滞模型计算成本高,静态参数的辨识依赖于大量实验数据的准确性,在工程中的应用性低。

鉴于上述问题,椭圆回线面积等效法(Equivalent Elliptical Loop,EEL)椭圆等效模型基于磁滞回线等效的思想,用椭圆回线描述磁滞回线,将磁场强度划分为可逆磁场强度和不可逆磁场强度,并对铁心损耗与椭圆回线面积进行数值等效。文献[15]基于EEL椭圆模型,建立了等效磁场强度随磁通密度、频率等参数的变化规律,推导了无直流偏磁下PWM励磁的磁心损耗模型;进而根据直流偏磁下磁心损耗的测量结果及其特征分析,构思了直流偏磁条件下PWM励磁的磁心损耗模型。文献[16]基于EEL等效椭圆模型,采用磁通密度幅值、磁场强度幅值以及频率表示损耗分离法中的磁滞损耗系数kh,提出磁滞损耗的时域计算模型,并结合磁通密度轨迹的拐点建立瞬态损耗建模算法。文献[17]将等效椭圆模型与损耗分离模型相结合,建立铁磁材料时域动态磁滞模型,该模型能应用于与二维和三维有限元分析,并以良好的精度预测瞬时磁滞损耗。EEL等效椭圆模型具有表达形式简单、参数少、计算简便的优势;但其在计算接近饱和磁通密度情况的铁心损耗时存在一定程度的局限性,同时现有文献鲜有对EEL模型在谐波工况下损耗计算的系统研究。

综合上述问题,本文基于铁磁材料的磁特性测试与数据分析,充分考虑磁化频率和磁通密度对磁滞回线形状的影响,结合磁性参数,对饱和磁滞回线进行有效的形状表征,建立正弦高磁通密度情况下的改进EEL椭圆模型;同时针对谐波激励工况,有效考虑畸变磁通所引起的局部磁滞回环对磁损耗的影响,采用磁滞回线解耦方式,分别对主磁滞回环与局部磁滞回环进行等效处理,进而建立谐波激励下的损耗模型,扩展了EEL损耗模型的适用范围,以实现对磁损耗的高效求解。最后将实验测量值与上述模型的解析计算结果进行对比,验证了文中所提磁损耗方法具有较高的计算精度和工程适用性。

2 传统EEL损耗模型

基于回线面积等效思想,文献[14]提出使用EEL计算铁心损耗,该方法将磁场强度分离为可逆分量Hrev及不可逆分量Hirr两部分,认为磁滞损耗仅与不可逆分量有关,并将不可逆分量等效为标准椭圆回线,如图1所示,通过计算标准椭圆回线的面积便可得到磁滞损耗。

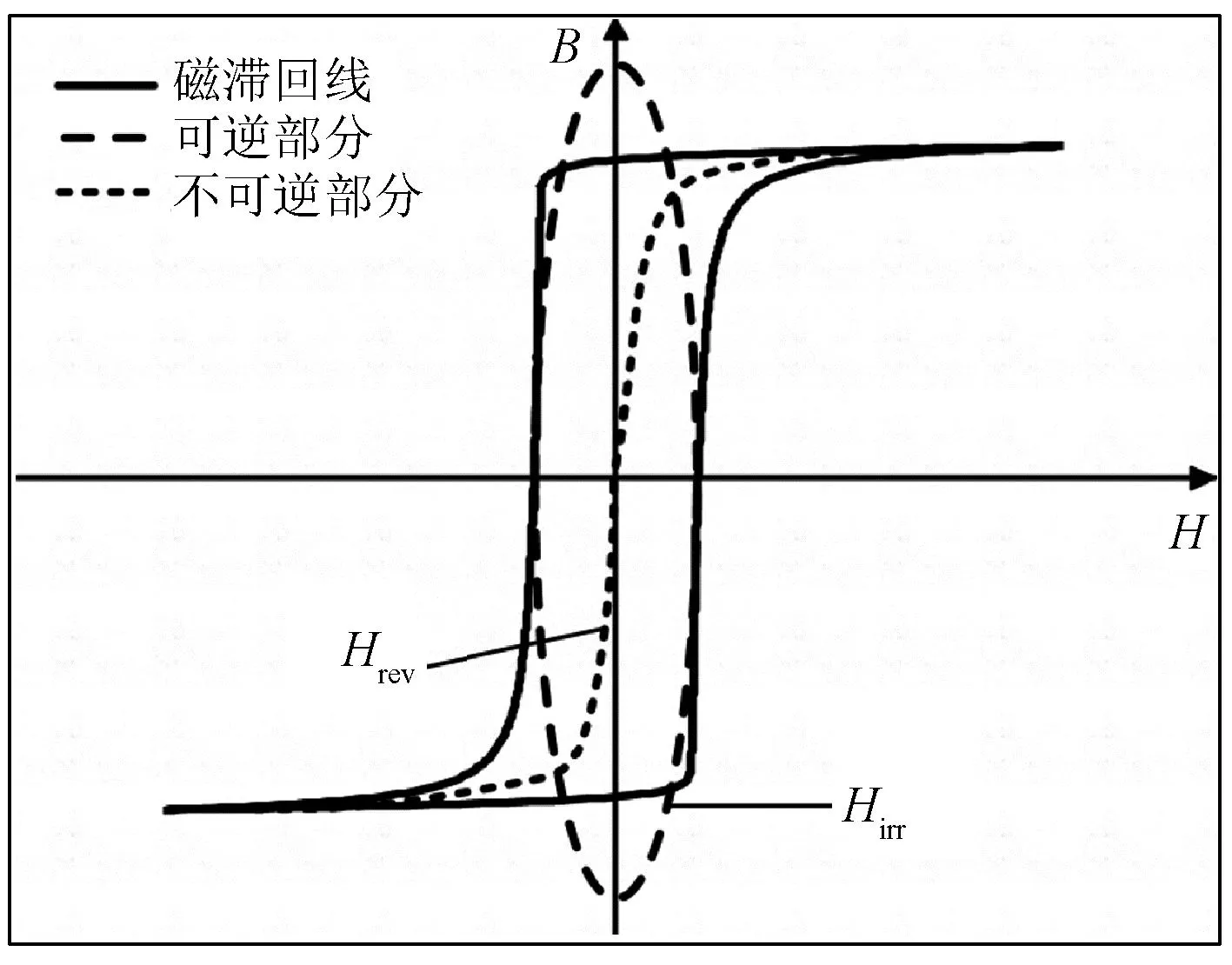
图1 磁滞回线与等效椭圆回线Fig.1 Hysteresis loop and equivalent elliptic loop

动态磁化是指铁磁性材料受交变磁场而发生的周期性重复磁化过程。铁磁性材料在动态磁化时,经过一周的磁化,其单位体积的磁损耗数值与其动态磁滞回线所包围的区域面积相等。动态磁滞回线在外形上和静态磁滞回线类似,但在结构上,动态磁滞回线所包含的区域更大。这是由于铁磁性材料在静态磁场下仅有磁滞损耗,而在动态磁场下不但有磁滞损耗,还有涡流损耗和异常损耗。因此,可以通过对由动态磁化引起磁滞回线所包围区域面积的计算,来获得一个磁化周期中铁磁材料的总磁损耗[18]。

根据等效椭圆法[15]可得标准椭圆回线的数学模型为:

(1)

式中,Hirr为不可逆磁场强度分量;Hm为磁场强度幅值;Bm为磁通密度幅值;ω为角速度。则铁磁材料在一个磁化周期T内的单位体积磁损耗可表示为:

=πfHmBm

(2)

式中,f为磁化频率。

考虑到交变磁场的磁化频率和磁化强度是影响EEL损耗模型计算精度的主要因素,本文选取牌号为B30P105的取向硅钢片作为试验样件,基于爱泼斯坦方圈实验测量系统进行损耗测量。设置激励源为正弦激励,从磁化频率和磁场强度两个角度出发对EEL损耗模型进行验证。如图2所示,在频率变化的情况下,EEL损耗模型在中等磁场或弱磁场励磁条件下的计算精度非常高;然而,当磁通密度幅值增大到1.7 T时,损耗计算结果出现了较大误差,可见在接近饱和磁通密度时EEL损耗模型已经不再适用。

图2 正弦激励EEL模型预测值与实际值对比Fig.2 Comparison between predicted value and actual value of sinusoidal excitation EEL model

从铁磁材料磁化机理的角度分析,在低磁通密度励磁条件下,铁磁材料的磁化机制以畴壁位移为主;随着外磁场的不断增大,畴壁位移基本完成,此时铁磁材料的磁化机制以磁畴转动为主;当外磁场增大到一定程度时,畴壁位移及磁畴转动都已基本完成,此时铁磁材料的磁化强度大致稳定不变,磁化逐渐趋于饱和,其宏观表现为磁滞回线逐渐由椭圆形变为S形,以50 Hz为例,如图3所示。

图3 50 Hz时的磁滞回线簇Fig.3 Hysteresis loop cluster at 50 Hz

本文针对高磁通密度励磁条件下EEL损耗模型无法有效考虑铁磁材料磁滞回线形状变化导致损耗计算误差较大的问题,将从完善模型物理机理及优化模型计算精度的角度出发,提出一个反映磁滞回线形状变化的回线形状因数,对饱和磁滞回线进行有效的形状表征,建立能够准确计算饱和磁通密度磁损耗的改进EEL损耗模型。

3 改进EEL损耗模型

传统EEL损耗模型在低磁通密度情况下展现了较好的计算精度,但其在处理高磁通密度条件下的损耗计算时仍存在缺陷。EEL损耗模型改进的关键在于寻求一个既能有效反映磁滞回线形状变化,又能准确描述动态磁化过程中损耗特性的形状因数,从而可以对饱和情况的磁滞回线进行有效表征。为此,本文以铁磁材料的磁性参数及磁场基本物理量为基础,结合大量实验数据进行形状因数的拣选及确定,并联系交变磁场的磁化频率和磁化强度得到EEL损耗模型修正系数KE。综上所述,本文建立的改进EEL损耗模型可以表示为:

P=KEPEEL

(3)

式中,P为正弦激励下铁磁材料磁化一周单位体积的总损耗。

3.1 改进损耗模型的建立

矫顽力HC和剩余磁感应强度BR描述了铁磁材料在外加磁场作用下达到饱和磁化时的基本磁特性,是铁磁材料的重要磁性参数。为了便于数据处理和实验分析,本文将其重新定义并推广到未饱和磁化的情况。在任意外部磁场情况下,HCA为磁感应强度为零时的磁场强度,BRA为磁场强度为零时的磁感应强度,磁滞回线如图4所示。

图4 磁滞回线及参数定义Fig.4 Hysteresis loop and parameter definition

技术磁化中常用矩形比R来表征磁滞回线的矩形程度,将其定义为剩余磁感应强度BR与饱和磁感应强度BS之比,即R=BR/BS。但是实际情况铁磁材料往往未达到饱和磁化,为此本文结合磁通幅值Bm和磁场强度幅值Hm,提出使用形状因数RB、RH以及RBH描述磁滞回线的形状特性,将其分别定义为RB=BRA/Bm、RH=HCA/Hm、RBH=Bm/Hm,并结合实验数据对三者进行对比分析。以频率50 Hz为例计算不同形状因数数值,如图5所示。图5中,KE-M=PM/PEEL,PM为铁心损耗实量值。尽管RBH在数值上与KE-M并不完全匹配,但是其变化趋势与KE-M一致,能够准确表征动态磁化过程中的损耗特性,因此选择RBH为修正系数中的形状因数。

综合考虑频率以及磁通密度的影响,在形状因数基础上引入KE1、KE2表征不同频率不同磁通密度,基于上述分析结果,本文提出的修正系数KE表达式为:

(4)

依据式(4)中参数KE1、KE2随磁化频率f的变化趋势,如图6所示。

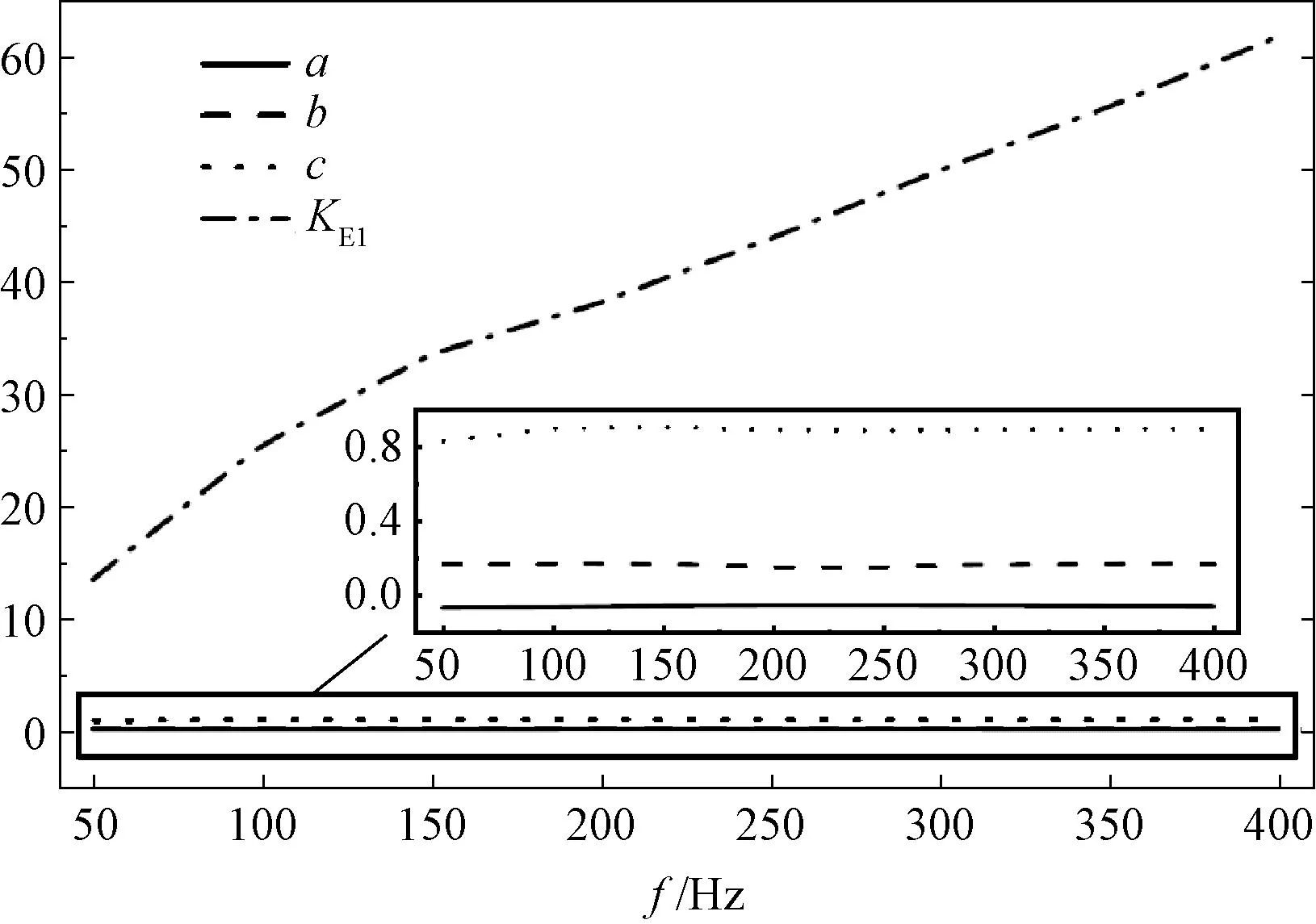
图6 KE1、KE2各参数随频率变化趋势Fig.6 Variation trend of KE1 and KE2 parameters with frequency

可见KE1是关于频率f的一次函数;KE2是关于磁通密度幅值Bm的表达式,对其进行回归拟合,得到参数函数关系式:

(5)

式中,m、r、a、b、c为模型参数。经过回归分析后求得参数见表1。

表1 仿真模型的参数Tab.1 Parameters of simulation model

综上所述,针对正弦激励条件,建立了可以考虑材料饱和磁化特征并能够适用于高磁通密度情况的改进EEL损耗计算模型为:

P=KEPEEL

(6)

(7)

3.2 改进损耗模型的验证

为了探究正弦激励下高磁通密度EEL损耗模型的准确性,本文旨在从工程应用和理论研究两个方面,聚焦于叠片电工钢材料,选取牌号为B30P105的取向硅钢片作为试验样件,搭建了铁心交变磁特性实验测量平台。该系统主要由信号发生器、功率放大器、功率分析仪以及标准爱泼斯坦方圈组成。测试平台的设备连接图和原理图分别在图7和图8中显示。实验获得磁化频率50～400 Hz范围内的正弦磁损耗数据。信号发生器和功率放大器组成测试系统的激励源部分,信号发生器产生不同频率的信号,在经过功率放大器放大处理之后,输出稳定可靠的激励信号;待电压稳定后,功率分析仪用来采集与分析测试结果,获得被测样件上施加的激励电压波形、励磁感应电流波形以及损耗值。通过对感应线圈的实验测量,借助Matlab软件编程处理,可应用电磁感应定律计算得到B-t曲线即磁通密度波形;基于实验所测的励磁电流波形,利用安培环路定理求得实验测量过程中的磁场强度波形H-t曲线,结合测得的磁通密度B,进而绘制出各种激励工况下铁磁材料的磁滞回线,继而得出铁心的损耗特征曲线。

图7 磁性能测试系统实物图Fig.7 Physical drawing of magnetic property test system

图8 磁性能测试系统原理图Fig.8 Schematic diagram of magnetic test system

基于以上分析,对本文所提正弦改进损耗计算方法进行相关的实验验证,磁损耗计算值与实测值对比如表2、图9所示;可以看出,上述模型可以准确获取不同磁通密度和不同频率正弦工况下的磁损耗计算结果,模型计算值与实测结果吻合较好,特别是在高磁通密度情况下同样体现了高度的准确性,验证本文所提模型的有效性,并为相应条件下磁损耗预测提供技术支撑。

表2 改进EEL损耗模型磁损耗计算值与实测值对比(Bm=1.7 T)Tab.2 Calculated magnetic loss of the improved EEL loss model was compared with the measured value(Bm=1.7 T)

图9 改进EEL损耗模型的验证Fig.9 Validation of improved EEL loss model

4 谐波激励EEL损耗模型应用

4.1 谐波激励控制

为了探究谐波工况损耗的计算方法,采用图7测试平台对不同阶次、不同含量、不同相位谐波条件下的磁损耗及磁特性进行测量。谐波激励的表示方法比较繁杂,需使用3个特征量:谐波阶次、谐波含量变化以及谐波相位差才能精准刻画。采用磁通密度可控的方案,通过调节激磁电压波形获得所需要的谐波工况下磁通密度波形为:

(8)

式中,φ1为基波相位,在本实验中取0°;U(t)为电压控制函数;φn为n次谐波分量相位,0°≤φn≤360°;n为谐波阶次;N为线圈匝数;S为硅钢片叠片横截面积;B1为基波磁通密度幅值;Bn为第n次谐波分量的磁通密度幅值;kn为n次谐波在基波中所占的含量;θn为n次谐波与基波的相位差。

4.2 谐波激励EEL模型

实验测得相应谐波工况下的磁滞曲线,以局部回环存在较为清晰明显的基波叠加30%相位为0的三次谐波为例,发现在任意谐波激励工况下,当磁通密度波形发生局部波动时,会对应出现局部磁滞回环,如图10所示;与仅能产生主磁滞回环的激励源相比,激发了局部磁滞回环的非正弦激励损耗计算更加困难。为了准确计算谐波工况下的磁损耗,将主磁滞回环与局部磁滞回环分别进行处理,计算两者对应的损耗值,再将两者归并得到总损耗。采用磁滞回线解耦的方法,将磁滞回线分解为主磁滞回环与局部磁滞回环两部分,如图11所示。

图10 谐波磁通密度波形及磁滞回线Fig.10 Harmonic hysteresis loop

图11 谐波磁滞回线解耦Fig.11 Harmonic hysteresis loop resolution

由图11可以看出,主磁滞回线的形状与正弦工况下的磁化曲线形状相似,因此可以将主磁滞回环等效正弦化,再结合上述正弦改进EEL损耗模型对谐波主磁滞回线损耗进行求解;对于分解后的局部磁滞回环,将其近似成椭圆形状,再利用EEL损耗模型计算,近似后的曲线如图12所示,图12中的实线段为谐波激励工况下的磁滞回线,虚线部分为等效后的磁滞回线,具体计算模型表达式为:

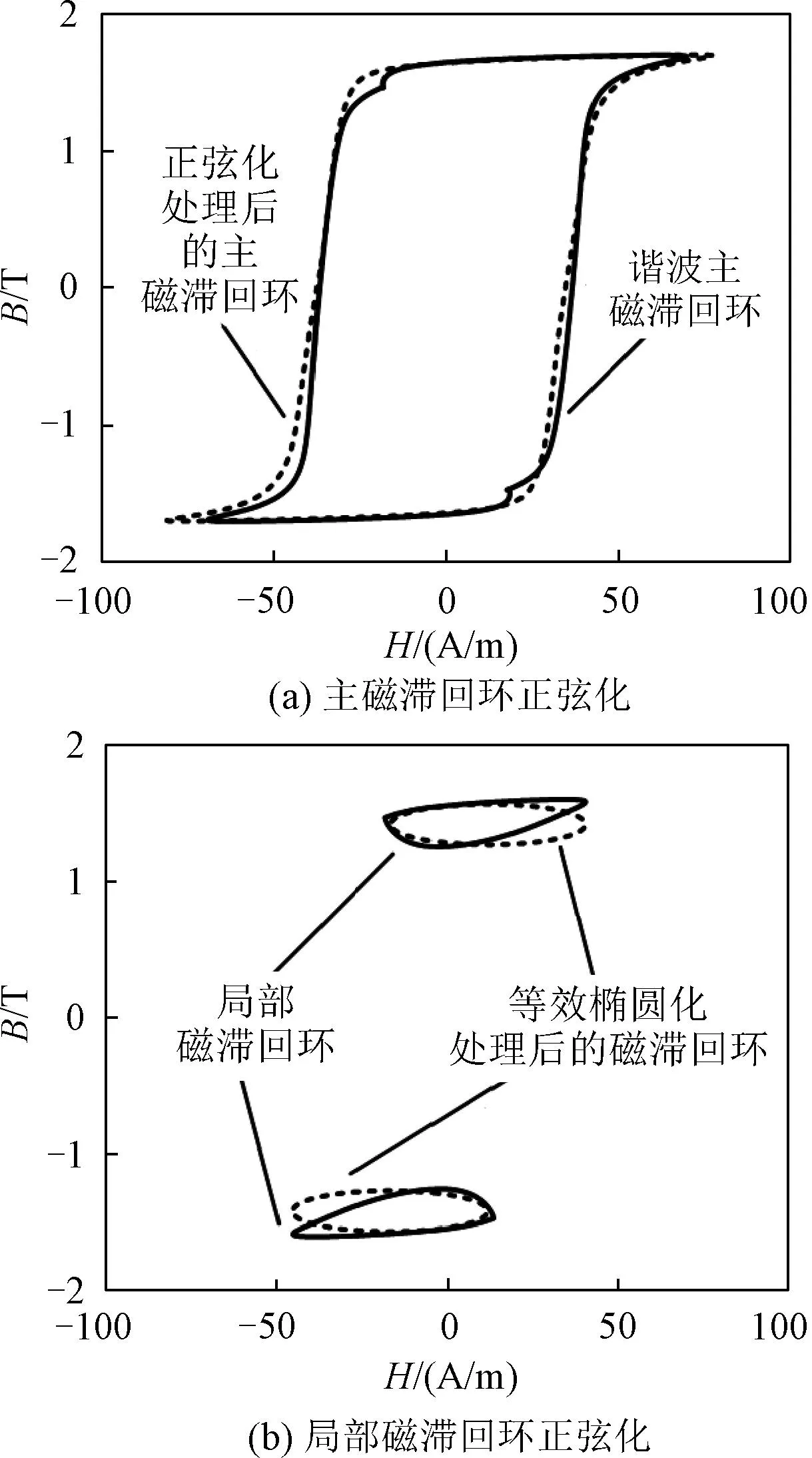
图12 谐波磁滞回线正弦化Fig.12 Harmonic hysteresis loop sinusoidal

(9)

式中,PHAR为谐波激励下铁磁材料磁化一周的总损耗;Pmajor为主磁滞回环损耗值;Pminor为局部磁滞回环损耗值;损耗修正系数KE取对应频率下的数值;Bi、Hi、fi分别为局部磁滞回环的磁通密度幅值、磁场强度幅值及频率;i为局部小回环个数。研究发现,局部磁滞回环其位置关于坐标轴是对称分布的,它们的形状、大小近乎相同,因此可以认为不论是磁化回路还是反磁化回路上的局部磁滞回环,其对磁损耗特性产生一样的影响,从宏观上看导致增加的损耗大小也是一致的。

目前研究谐波工况时,通常从影响磁通密度波形发生畸变的三要素:谐波阶次、谐波幅值以及谐波相位出发,表征磁通密度畸变波形。为合理描述磁损耗与磁通密度波形畸变程度的相关性,体现谐波激励特性,综合考虑谐波阶次以及Bm、Bn的影响,本文提出在式(9)基础模型上引入谐波修正系数KHAR来描述磁通密度的畸变程度[19,20]:

(10)

即:

PHAR=KHAR(Pmajor+Pminor)

(11)

基于3.1节中提出的谐波EEL损耗模型,逐一从不同谐波阶次、不同谐波含量变化、不同谐波相位差三个方面对磁损耗进行实验计算验证,以Bm=1.7 T为例,得到结果见表3～表5。

表3 不同谐波阶次磁损耗计算值与实测值对比Tab.3 Calculated values of magnetic losses of different harmonic orders compared with measured values

表4 不同谐波含量磁损耗计算值与实测值对比Tab.4 Calculated values of magnetic losses of different harmonic content compared with measured values

表5 不同谐波相位磁损耗计算值与实测值对比Tab.5 Calculated values of magnetic losses of different harmonic phases compared with measured values

针对基波叠加多次谐波的工况,本文仍采用式(11)模型求解,当Bm=1.7 T时,求解结果见表6。通过对比结果可以看出,本文所提磁损耗计算模型在多次谐波工况下同样适用,且误差较小,效果较好。

表6 基波叠加多次谐波磁损耗计算值与实测值对比Tab.6 Calculated value of multiple harmonic magnetic loss of fundamental wave superposition compared with measured value

通过表3～表5可以看出,本文所提谐波激励条件下的磁损耗模型计算值与实验测量值之间的误差较小,验证了文中所提磁损耗方法的合理性和工程适用性。

5 结论

(1)正弦激励条件下,由于饱和磁化对磁滞曲线形状的影响,致使EEL椭圆模型在饱和磁通密度情况下不再适用。本文基于铁磁材料磁特性测试与数据分析,从完善模型物理机理及优化模型计算精度的角度出发,综合考虑磁化频率和磁通密度的影响,对饱和磁滞回线进行有效的形状表征,建立了正弦EEL改进损耗模型。

(2)本文有效考虑了谐波激励条件下局部磁滞回环对磁损耗的影响,将主磁滞回环与局部磁滞回环分别处理,并对其进行近似等效,进而建立了谐波工况下的损耗模型,实现了磁损耗的有效计算,扩展了EEL损耗模型的适用范围。

(3)本文通过搭建复杂工况磁特性测量装置进行相关实验验证,验证了文中所提磁损耗方法具有较高的计算精度和工程适用性。文中改进EEL等效损耗模型,形式简洁,计算量小,能够为变压器优化设计阶段的铁心损耗计算提供支撑。