压差式静力水准成果数据滤波和预测算法研究
2024-01-08张子真周宏磊张建坤贾辉
张子真,周宏磊,张建坤,贾辉
(北京市勘察设计研究院有限公司,北京 100038)
0 引 言
2011年至今,我国城市地下空间飞速发展,地下空间开发规模达“千万级”的城市屡见不鲜,地下空间开发深度的纪录也在不断刷新。然而,地下空间开发施工过程中,必须对周边环境进行持续监测,以确保安全。有些既有建(构)筑物对变形监测的要求非常严格,以地铁为例,其允许变形值往往只有3~5 mm,这给监测精度提出了极高的要求。
目前,静力水准是进行沉降自动化监测的常用手段,根据伯努利原理,静力水准可以测量出各测点在任意时刻的高程,然后再计算累计沉降量。静力水准受环境因素,例如气压、振动、温度等影响明显,未经滤波处理的数据,表现出极大的噪声,难以满足实际工程精度需求,需要对监测成果进行滤波处理。另外,静力水准积累的大量数据,也给预测算法的实现创造了可能。
本文主要研究了滑动平均法、中位值法、中位值平均法、限幅法和3σ准则法等5种滤波方法对静力水准成果数据的降噪效果,并在此基础上,提出了预测算法,然后将滤波和预测算法编入了自动化监测信息平台,可用于实际生产应用。
1 滤波方法
1.1 滑动平均法
当信号在某一数值范围附件频繁波动,可滑动平均法,它适用于对随机干扰信号的处理,例如流量、液位测量等。滑动平均法历史悠久、方法简捷,计算量小。它分为简单滑动平均法和加权滑动平均法[1]。
其基本方法是,连续取N个测值计算算数平均值。显然,当N较大时,滤波后的平滑度较高,但灵敏度降低,反之,平滑度降低,灵敏度提高,如图1所示。

图1 滑动平均法效果示意图

图2 中位值滤波法效果示意图
1.2 中位值滤波法
当测值变化缓慢,可推荐采用中位值滤波法,当测值变化迅速时,则不建议采用该方法。中位值滤波法尤其擅长处理偶然因素引起的扰动或误码等脉冲干扰。中位值滤波是一种典型的非线性滤波方法。改进的中位值滤波算法包括中心加权中位值滤波算法[2]、开关中值滤波算法[3]、自适应中位值滤波算法[4]等。其基本方法是,连续采样N次(N是奇数),然后把采样值从小到大排列,取中间值为滤波结果。
1.3 中位值平均滤波法
中位值平均滤波法又称防脉冲干扰平均滤波法,可消除偶然脉冲性干扰,抑制周期性干扰,适用于高频振荡系统。中位值平均滤波法应用广泛,它融合了滑动平均法和中位值滤波法的特点,其基本方法是,连续采集N个数据,剔除它们中的最大值和最小值,然后取剩下数据的平均值为滤波结果,如图3所示。它虽然可以有效滤除偶然脉冲雨后春笋,但反应速度慢。

图3 中位值平均滤波法
1.4 限幅滤波法
限幅滤波法是应对随机干扰的另一种方法。它[5]分为传统滤波法、迭代限幅滤波法,可变限幅滤波方法等,它可有效降低峰均比,抑制高频噪声。其基本方法是,比较相邻N和N-1时刻的两个采样值s(N)和s(N-1),如果两次采样值的差值超过最大偏差,删除y(N),然后用y(N-1)代替y(N);若未超过所允许的最大偏差,采用本次采样的s(N)。最大偏差值是根据经验来确定的。
根据长期既有线监测经验,确定静力水准最大偏差值 1 mm,处理效果如图4所示。
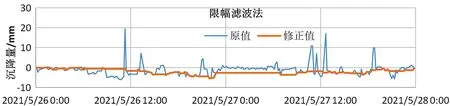
图4 限幅滤波法效果示意图
1.5 3σ准则滤波法
当数据量较大,且服从或近似服从正态分布时,可采用3σ准则,也叫拉伊达准则,该方法是用来剔除粗大误差的[6],先按一定概率确定一个区间,认为超过这个区间的误差属于粗大误差,并予以剔除。
在正态分布中σ代表标准差,μ代表均值。x=μ即为图像的对称轴。
数值分布在(μ-3σ,μ+3σ)中的概率为 0.997 3。可以认为,取值超过(μ-3σ,μ+3σ)区间范围的概率不到0.3%。
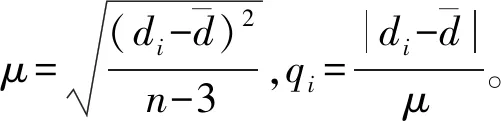
当qi>3时,认为xi是奇异值,应予以舍弃。效果如图5所示。
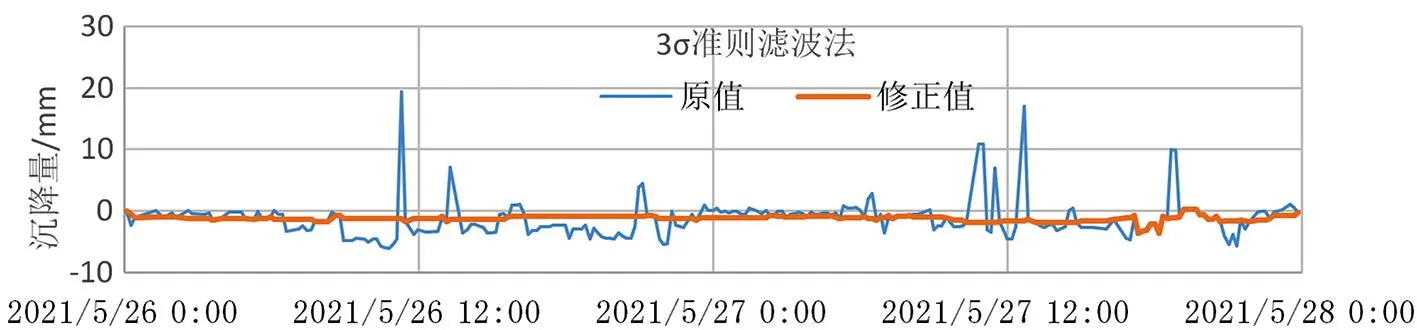
图5 3σ准则滤波法效果示意图
2 滤波算法应用效果分析
第1.1节~1.5节是对静力水准的成果数据进行滤波处理,将滤波后成果放在一起,如图6所示,从中可以看出,虽然原值是相同的,但不同的滤波方法,会得到不同的滤波效果。限幅滤波法的成果要更平缓一些,而算法平均法波动得最严重。
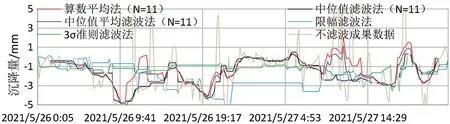
图6 滤波后成果对比
中位值滤波法可以很好地将脉冲噪声滤除掉,例如图7所示,但是对于小范围的波动,则并没有起到很好的处理效果。
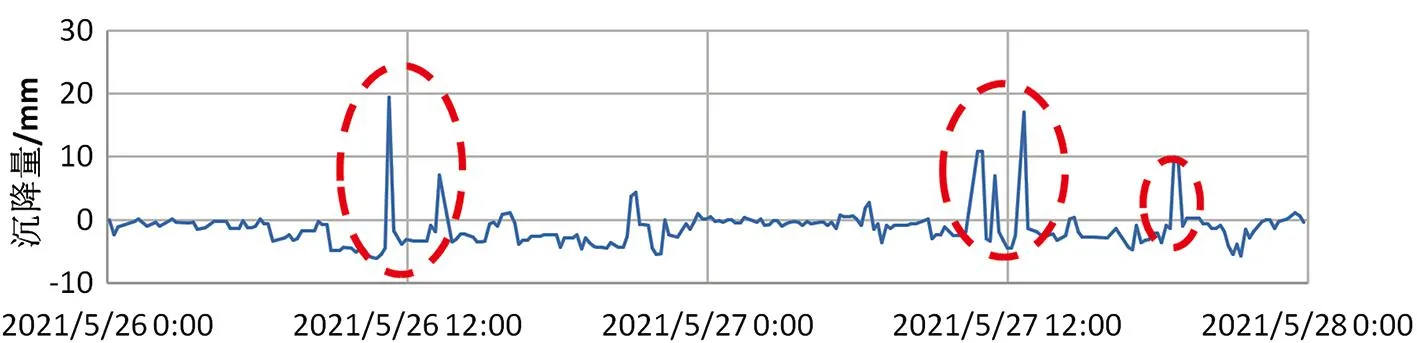
图7 脉冲噪声
滑动平均法、3σ准则滤波法、中位值平均滤波法比较适用于服从正态分布的数据,为了验证图6的不滤波成果数据是否服从正态分布,可以对其进行卡方检验。
卡方检验的原理是,假设样本服从正态分布,样本容量是n,按其大小分布范围,划分为互不统属的k个区间,统计落入每个区间的频数Oi,计算每个区间的理论频率pi和理论频数npi,最后计算卡方值,卡方值服从自由度为k-s-1的卡方分布,即:
求出事件发生的概率值,当其小于显著性水平0.05时,则说明数据不服从正态分布,当概率值大于0.05时,则判断数据服从正态分布。
图6的不滤波成果数据,样本容量n=245,最大值是19.40,最小值是-6.10,极差为25.5,分为k=11组,平均值是-1.29,标准差是3.04。最终卡方值是 311 158 634,自由度是8,概率是0.00<0.05,所以数据不服从正态分布,如图8所示,因此滑动平均法、3σ准则滤波法,以及中位值平均滤波法并不完全适用于静力水准的成果数据分析。

图8 概率分布直方图
限幅滤滤法可以用来处理脉冲噪声,但要求对系统的采样数据范围要有准确的判断,否则如果允许误差值设置不合理,可能会将系统中正常的数据滤掉,例如图9~图12是同一组数据采用限幅滤波法处理,采用不同的最大偏差值所得的结果,可见最大偏差值设定越小,曲线越平滑,但这也可能丢失掉一些重要的真实变化数据。
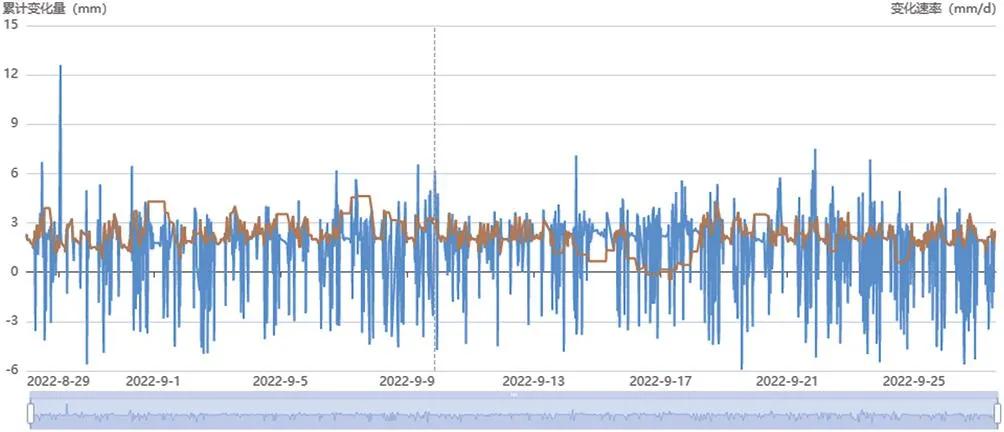
图9 限幅滤波法(最大偏差值:1 mm)
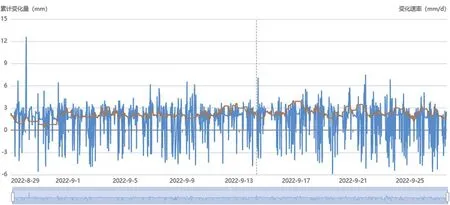
图10 限幅滤波法(最大偏差值:0.5 mm)
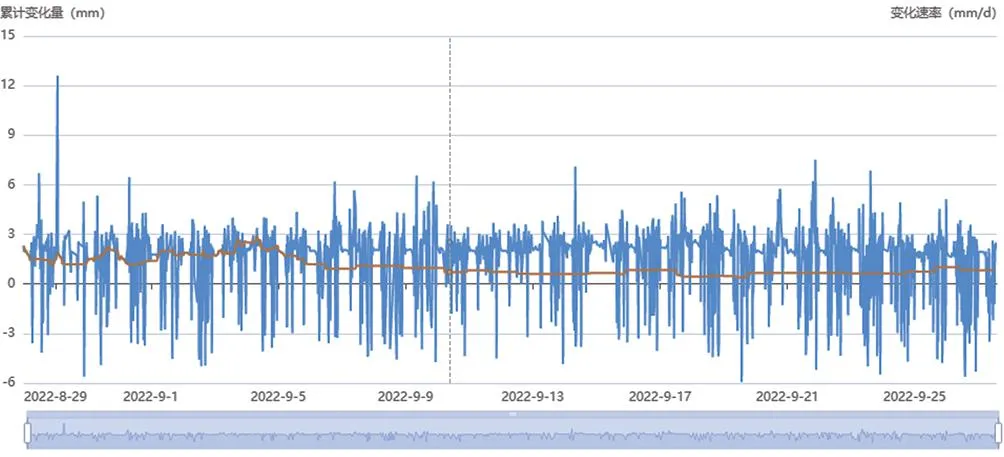
图11 限幅滤波法(最大偏差值:0.3 mm)

图12 限幅滤波法(最大偏差值:0.1 mm)
3 数据预测算法研究
选择一段既有数据,对一条曲线进行拟合,然后将拟合后的曲线,向未来延伸,即得到一条预测曲线,这是预测算法的思路,如何选择用于拟合的成果数据,是本任务的关键。如果滑动平均法、中位值滤波法、中位值平均滤波法、限幅滤波法、3σ准则滤波法等5种方法滤波后的数据直接拟合,如图13所示,相关系数R=0.5,中度相关,相关程度较低,这主要是因为,滤波后的成果,仍然带有较大的离散性。
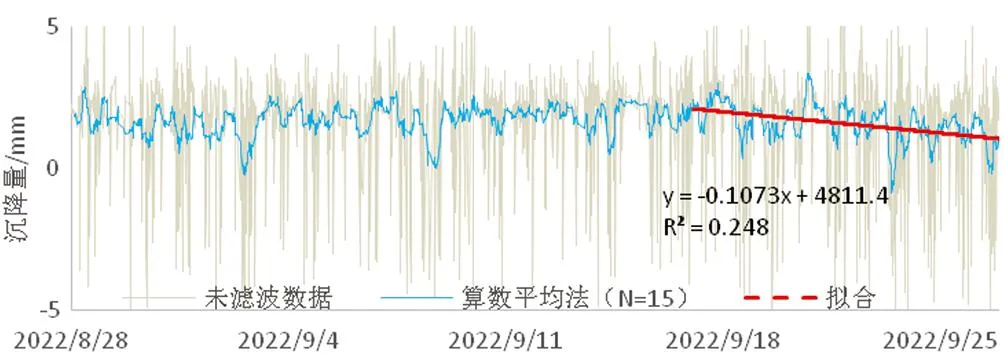
图13 未考虑卡尔曼滤波的拟合结果
卡尔曼滤波处理后的数据,收敛性很好,如果将滤波后的成果数据,再进行一次卡尔曼滤波,然后用卡尔曼滤波后的数据,去拟合曲线,效果会更好,如图14所示,相关系数达到0.89,达到高度相关水平。
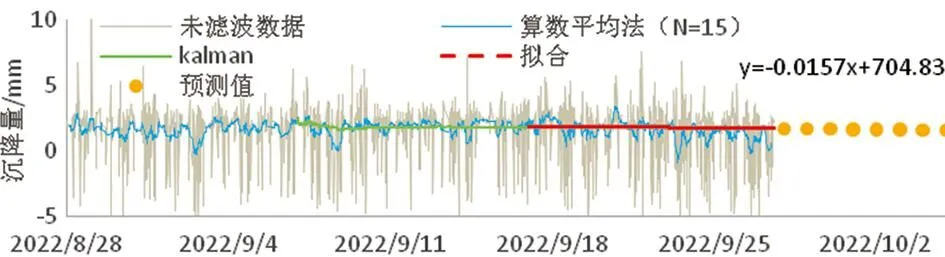
图14 未考虑卡尔曼滤波的拟合结果
根据上述效果对比,提出以下预测算法步骤:
(1)对原成果数据,任选五种滤波方法其一,进行处理。
(2)从当前时刻倒推2N天时间,对滤波后的数据,进行卡尔曼滤波处理。
(3)从当前时刻倒推N天时间,利用卡尔曼滤波成果,进行预测曲线进行拟合。
(4)拟合曲线向未来延伸,视作预测数据。
目前,已将滤波和预测算法编入自动化监测信息平台,如图15所示。蓝色曲线表示未经处理的成果数据,橙色曲线表示经过移动平均后的成果数据,灰色曲线表示卡尔曼滤波处理后的曲线,拟合部分未在图中表示,最后绿色曲线表示预测的变形趋势。

图15 滤波和预测成果
4 结 论
(1)选择滑动平均法、中位值滤波法、中位值平均滤波法、限幅滤波法、3σ准则滤波法,可以对静力水准成果数据进行滤波处理。中位值滤波法对脉冲噪声有明显降噪作用,滑动平均法、中位值平均滤波法、3σ准则滤波法在数据服从正态分布时,效果更好,限幅滤波法对参数选择的敏感度很大。
(2)通过对滤波后的成果数据,再进行一次Kalman滤波,可以明显提高预测曲线拟合的相关系数,从而实现预测算法。
