卫星三平面法动平衡试验方法及在轨实践

2024-01-08张天赫吴成松陆姗姗张文巧

上海航天 2023年6期

张天赫，吴成松，陆姗姗，张文巧，刘瑞，诸成

（1.上海微小卫星工程中心，上海 201203；2.中国科学院微小卫星创新研究院，上海 201203）

0 引言

随着航天技术的迅猛发展，为了满足不同功能需要，遥感卫星的对地观测载荷也由单一、固定遥感载荷向大型、回转、低速跟踪的遥感载荷方向发展［1-2］。同时伴随卫星平台小型化、星载一体化理念的不断发展，载荷的质量、惯量占比整星的比例越来越高。回转体载荷由于制造、装配、轴承晃动、精度偏差等多方面原因导致其自身质量分布存在偏差，自身惯量轴与旋转轴存在偏差进而引起回转体载荷的动不平衡。因此对于带有回转体类载荷的卫星，其回转体载荷的动平衡指标的提升是卫星在轨实现高精度观测的重要影响因素。

动平衡这一概念最早起源于带有转子的旋转机械行业，各种分析理论及动平衡机应用主要集中在汽轮机、发电机、电动机、离心机以及气体压缩机［3］。而对于卫星在太空微重力环境下，回转载荷支撑和润滑状态与地面设备大不相同［4］。因此卫星对回转体载荷的动平衡指标要求更高。目前国内外对动平衡研究主要集中在动量轮等小质量、小惯量回转体上［5-8］，如LIU 等主要对欧洲某太阳观测卫星上的反作用飞轮的高速转动不平衡干扰进行了建模、分析及验证，赵煜等对反作用飞轮的扰动特性进行了测量及研究，并评估了对主要解决了高速旋转体的动不平衡对寿命、对卫星姿态干扰的影响。

在大型回转体的低速动平衡研究方面，牛宝华等［9］开展了对海洋二号微波辐射计的动平衡仿真及试验方案进行了设计及验证工作，通过仿真分析及试验结果明确了柔性体天线刚性支撑下的动平衡试验方法必要性及有效性。薛孝补等［10］为实现对带旋转体卫星姿态的高精度控制，在卫星姿控动力学模型中引入转动部件动不平衡干扰动力学模块，通过对动不平衡的干扰力及干扰力矩进行试验配平，完成了低速、大质量旋转体动不平衡下的卫星姿态仿真并完成了在轨验证。然而，以上研究对于大质量、大惯量、低转速、高精度的回转体动平衡计算、测量、试验方法仍借助传统的旋转机械行业的相关理论方法。对于卫星而言，传统试验方法的配重质量、试验次数、试验时间等代价仍然较大，会对卫星的质量、卫星研制时间、回转体载荷地面转动寿命有较大影响。

本文根据既有双平面动平衡配平方法，基于双解耦立式动平衡机，提出了应用于卫星动平衡测试的三平面配平方法，并将该方法在某卫星星座研制中进行了工程实践。

1 双平面配平原理

双平面配平法是动平衡试验中常用的配平方法，假设有一连续转子离散为n个平面，则其不平衡质量分布图如图1 所示。

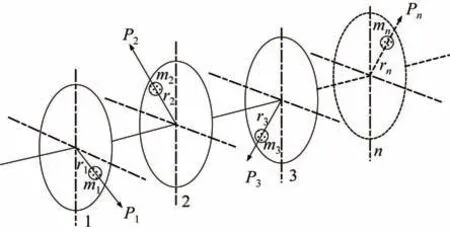
图1 转子动不平衡Fig.1 Dynamic unbalance of the rotating body

将每个平面不平衡量简化为不平衡质量mi，其不平衡矢径为ri，当转子以角速度ω转动过程中，等效偏心质量产生离心力Pi。对于双平面配平法，选取两处配平平面，将离心惯性力Pi分解至配平平面，如图2 所示。

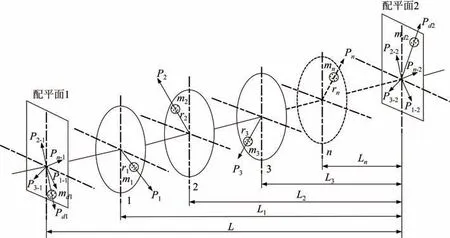
图2 双平面配平法原理Fig.2 Principle of the two-face balancing method

由以上可知，将n个不平衡离心惯性力分解至两个动平衡配平面1、2 上，在1、2 平面上形成空间力系，则有：

根据式（1）、式（2）可知，只需在配平面1 和配平面2 的相应矢径位置增加相应质量的配重即可以实现该回转体的双平面动平衡配平，这也是一般动平衡试验的常用配平方法。

2 低转速载荷卫星的动平衡试验原理

为实现回转体的双平面动平衡配平，使其在工程实践中能够得到应用，利用动不平衡的振动信号对其进行测量。对于高转速的回转体，其惯性力由于高转速的放大作用会提高信号的测量精度，能够将其从不平衡力矩信号中分离出来，进而完成动平衡的测量，通常这种回转体的动平衡测量采用硬支撑动平衡机测量。

而卫星的常用回转体载荷其转速较低，一般为10～30 r/min。在低转速的回转体动不平衡测量中，其离心力的大小取决于不平衡质量m和转速ω。而卫星载荷的旋转质量较小且低转较速使离心力产生的振动信号弱，并且力矩量远大于离心力，所以测量过程中力矩信号对离心力信号干扰严重［11］。同时受限于卫星构型特点，无法在卧式动平衡机上进行试验，而传统的硬支撑双面立式动平衡机有分离比差、测量精度低等问题［12-13］。因此，提出采用一种解耦式的新型立式动平衡机进行带有低转速载荷的某卫星动平衡测量。新式动平衡机原理如图3所示。

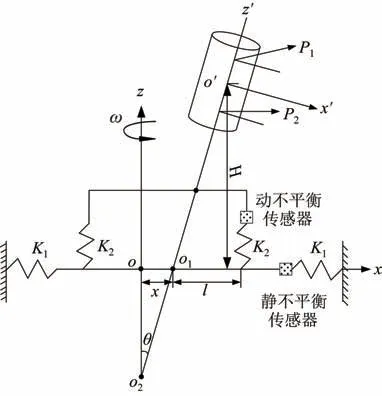
图3 动平衡测试原理模型Fig.3 Principle model of the dynamic balancing test

该动平衡机通过一套互相解耦的双主轴摆动系统实现对微弱的离心力信号进行解耦，利用K1平动板簧及K2摆动板簧分别获取离心力产生的平动振动及动不平衡产生的摆动振动，进而避免测量信号的混叠。如图3 所示，该模型描述了低转速、高精度的卫星回转载荷的不平衡测量方法。P1、P2分别为双平面不平衡法中配平平面的不平衡量，α1、α2分别为对应相位角。因为振动振幅较小，因此假定该系统的振动为小位移且忽略系统阻尼。

式中：m为振动系统总质量（包含两套摆动主轴系统、簧板、支架等）；m1为主轴系统质量；J为主轴系统的转动惯量；h为静不平衡至摆动中心位置即质心平面至摆动中心位置。

对式（3）、式（4）进行拉式变换，整理得：

式（5）、式（6）进行简化得到：

因该系统的支撑仍为双立面硬支撑系统，故ωn1≫ω，ωn2≫ω，即振动系统的平动固有频率、摆动频率均远大于测试回转体角频率，因此将式（7）、式（8）进行简化得到：

式中：Um、Vm分别为被测回转体的静不平衡量和偶不平衡量；α3、α4分别为Um和Vm的相位。

因此，双配平平面上的P1m、P2m不平衡量可以通过静不平衡和偶不平衡U、V来表达，如下：

式中：z1、z2为双平面配平法中配平面1、2 的纵向坐标。

由式（9）、式（10）和式（11）可知，通过对振动的解耦能够有效测量P1m、P2m及α1、α2。根据振动信号指示在相应平面进行加重，实现回转体的动平衡。

3 低转速载荷卫星动平衡试验系统

安装有低转速载荷的卫星在进行地面动平衡试验时，其载荷转动过程中由于结构、展开机构、热控多层等产生的空气阻力较大，而在太空环境为真空环境，因此对动平衡结果会产生较大影响。同时，卫星上旋转载荷的润滑方式一般为MoS2固体润滑，其转动过程中对环境的洁净度及湿度要求较高。

基于以上特点，结合立式硬支撑动平衡机的工作特点，本文设计了一个低转速载荷卫星动平衡试验系统。该系统由低压真空罐系统、动平衡机系统、测量数采系统、控制系统组成。试验系统组成如图4 所示。

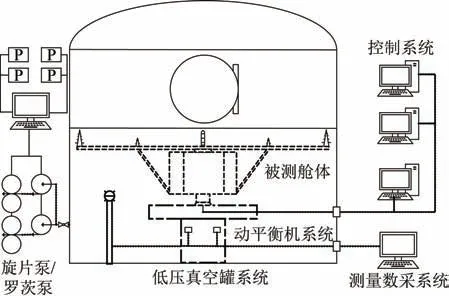
图4 动平衡试验系统Fig.4 Schematic diagram of the dynamic balancing test system

其中低压真空罐系统主要由低压真空罐、真空泵、真空罐控制台、液氮冷凝系统组成。真空罐采用二级真空泵系统，即旋片泵＋罗茨泵的形式，确保实现罐内低压。同时在真空罐与真空泵连接管道处安装液氮冷凝系统，实现防挥发确保罐内无挥发污染。动平衡机系统由立式动平衡机、转速测量系统、标准标校砝码组成。分别实现被测舱体的不平衡量测量、转速测量以及动平衡机精度标校。测量数采系统及控制系统通过罐壁上的真空插头连接转接电缆对被测舱体、动平衡机系统进行控制及数据采集。

本文构建的动平衡试验系统以低转速立式解耦动平衡机为测试设备，能够充分模拟被测舱体在太空中所处真空环境，可以实现真空度优于1 Pa 的常温真空环境，规避了常压下动平衡试验中空气阻力及多层状态对试验结果的影响，同时使转动载荷在充分保护下完成动平衡测量试验。

4 卫星动平衡三平面配平法

第2 节所述试验方法能完成低速回转体的动不平衡测量及双平面配平。虽然该动平衡测试理论能够实现低转速回转体的动平衡配平，但是双平面配平方法主要借鉴传统回转机械行业，应用在卫星的动平衡试验中主要有以下不足。

双平面法存在静平衡量与偶平衡量同时耦合配平，其配平质量的有效性、配平试验次数受到静不平衡量和偶不平衡量的相位α3、α4的影响较大，随机性较大，相位α3、α4与配平效率的关系如图5所示。

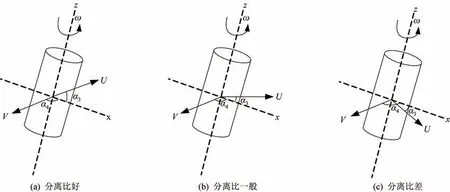
图5 双平面配平法效率Fig.5 Efficiency of the two-face balancing method

卫星回转体载荷是精密设备，其主要工作在微重力环境下，不承受重力，只承受旋转的不平衡力及力矩。因此对地面工作时间及转动次数均有严格的要求。地面转动次数过多，对载荷轴承、滑环的寿命均存在影响。而双平面法的随机性会增加配重质量、试验次数，造成配重质量的浪费及试验时长增加，并且因为双平面法的随机性，其高精度动不平衡指标的实现存在一定随机性，而卫星批产对指标一致性要求较高，因此不利于保持批产卫星的指标一致性。

采用第2 节的方法进行动平衡测量，该方法直接可以测量出静不平衡量及偶不平衡量。而双平面法并未充分利用直观的物理概念解决配平问题，而是通过式（6）对测量量转化得到物理意义不清晰的中间试验量。通过该方法实现高精度动平衡指标，需增加卫星舱体的配平孔位分布密度来适配配平角度，而卫星舱体为复核材料蜂窝板，对于安装孔位要进行埋件预埋，且质量代价较大，其孔位密度也存在一定限制。因此通过双平面法实现卫星舱体高精度动平衡指标存在一定困难。

从测量原理出发，解耦静偶不平衡量。通过测量得到的振动信号，选定质心平面作为静平衡配平平面，在舱体质心平面进行配平即能完成静平衡，并在试验前选定的两个平面作为偶平衡配平平面，进行配平即能完成偶平衡，即通过“三平面”法能够清晰快速的完成动平衡试验。根据式（5）可知，Um、Vm分别为被测回转体的静不平衡量和偶不平衡量，α3、α4分别为Um和Vm的相位。则有：

式中：m1、m2为偶不平衡量配平质量；z1、z2为对应平面的纵坐标，要求m1、m2的配平位置相位差为180°，m3为静平衡配平质量，配平平面为舱体质心平面，r3为其配平半径。工程实践中一般取r1=r2，则m1=m2。

5 实践及在轨评估

某型卫星星座共30 颗组网工作，分为10 批次发射，每组3 颗卫星，单星质量340 kg，载荷舱质量为128 kg。其载荷舱为一带展开机构的回转体舱体，展开后的回转直径为3 000 mm，转速为15 r/min。其回转舱体的结构形式如图6 所示。

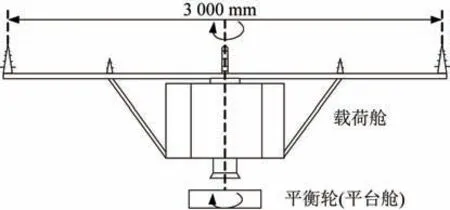
图6 卫星载荷舱Fig.6 Payload module of the satellite

根据前文所述动平衡试验方法，将卫星载荷舱体划分为3 个平面，卫星配平平面如图7 所示，其中双平面配平法采用图7 中的上下平面，三平面配平法采用图7 中的上中下3 个平面。其中中平面设置在舱体理论质心处，上下平面设置在舱体可设置配平平面的最大包络处。

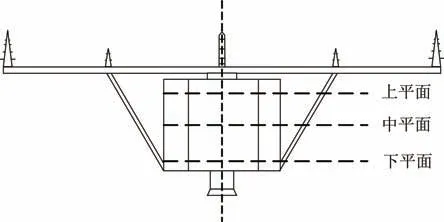
图7 卫星配平平面Fig.7 Balancing planes of the satellite

该卫星质量特性参数及转动特性见表1。其中首组3 颗卫星采用双平面配平法，后续27 颗采用三平面配平法。

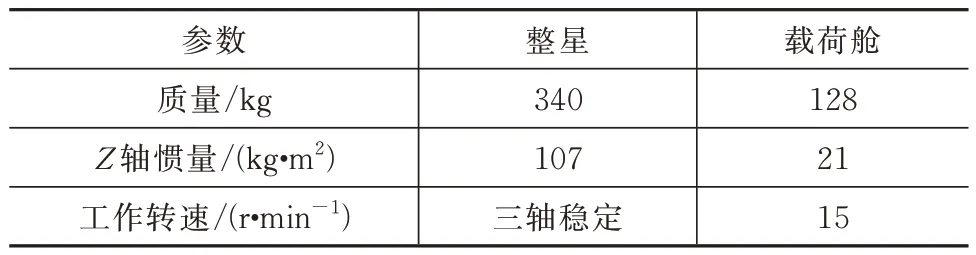
表1 被测卫星质量特性参数Tab.1 Mass property parameters of the tested satellite

首先对30 颗卫星的静不平衡量、偶不平衡量进行分析，被测卫星动平衡试验结果如图8所示，该卫星姿控分系统要求载荷舱的静不平衡量≤24 kg·mm，偶不平量≤20 000 kg·mm2，从图8 中可以发现采用两种方法对卫星进行配平，均能够实现动平衡技术指标要求，且有较大余量。由于实现动平衡精度较高，在低转速条件下，受到配重角度、配重质量近似的影响，试验结果存在一定随机性。

图8 被测卫星动平衡试验结果Fig.8 Results of the satellite obtained from the dynamic balancing tests

在两种试验方法均能够满足技术指标的情况下，分别从配重质量、试验时间、配平次数等试验过程数据方面对两种试验方法进行比较，如图9 所示。由图9 可知，与双平面法对比，三平面法在配重质量、试验次数、试验时长等方面均存在明显优势。

图9 被测卫星动平衡试验数据Fig.9 Data of the satellite obtained from the dynamic balancing tests

相比于双平面法，三平面法因配重不需要考虑相位角度的随机性，可以减少配重质量50%以上。因静偶不平衡量充分解耦，配重角度和质量更加准确，不需要近似，其试验次数及试验时间也大幅减少25%以上。因此，该方法的应用可以大幅减少配重质量，并且减少卫星载荷地面试验时间及试验次数。

为评估本文提出的三平面方法的有效性，本文进一步通过卫星遥测数据对不同动平衡试验方法的在轨效果进行评估。被测卫星在轨工作的控制策略为载荷舱开始旋转的同时转动轴方向的平衡轮开始工作，进行消旋，平衡轮只对旋转轴进行消旋，其余干扰均由整星姿控分系统进行控制。在载荷舱开始旋转180 s 后，卫星姿控分系统介入并对载荷舱动不平衡产生的整星干扰力及力矩进行控制。因此，通过载荷舱起旋180 s 内的其余两轴的姿态角速度工程遥测可以评估动平衡试验的在轨效果。

选择动平衡试验结果较为接近的03 星、04 星的工程遥测进行对比，其两星试验结果见表2。图10及图11 给出被测卫星03 星（双平面法）和04 星（三平面法）的偏航及滚转角速度工程遥测对比曲线。

表2 03/04 卫星动平衡试验数据Tab.2 Data of the 03/04 satellited obtained from the dynamic balancing tests

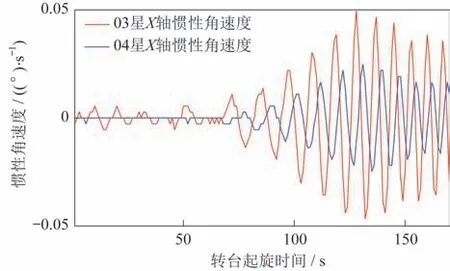
图10 被测卫星转台起旋姿态遥测数据（X 轴）Fig.10 Attitude telemetry data of the satellite when the payload module is rotating（X-axis）

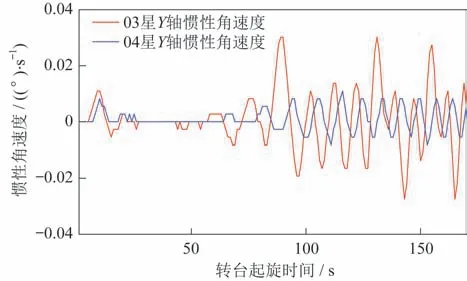
图11 被测卫星转台起旋姿态遥测数据（Y 轴）Fig.11 Attitude telemetry data of the satellite when the payload module is rotating（Y-axis）

从卫星在轨工作测试来看，03 星、04 星均能够正常开展工作，所有指标均满足要求。但从图10 与图11 对比曲线可以看出，在地面试验指标相近的情况下，三平面法的在轨实际效果明显优于双平面法，角速度动态量明显优于双平面法。载荷舱起旋过程中，三平面法配平的载荷舱对卫星的干扰力/力矩明显优于双平面法，其两轴的角速度幅值可以减少50%以上。较小的干扰代表卫星稳定控制更快，风险更低，姿控分系统介入后，卫星能够更快达到姿态控制指标要求，进入工作模式所需的时间更短。