多约束航迹规划与跟踪制导律
2024-01-08尹中杰杨建东刘艳斌蔡克荣
尹中杰,王 磊,杨建东,刘艳斌,王 楷,蔡克荣
(上海机电工程研究所,上海 201109)
0 引言
升力式飞行器是指能够在20~70 km 高度进行高机动飞行,可执行侦查与对抗等任务的飞行器。因其具有航程远、机动性强等优势,受到各国的重视。考虑到升力式飞行器在滑翔过程中存在多方面的过程、终端约束,其中的航迹规划以及跟踪控制律设计引起了国内外学者的广泛研究[1-4]。
滑翔段航迹规划是指在不违背热流、动压、过载等各种约束的前提下,通过制导控制将升力式飞行器引导至中末制导交班点的工作。研究大致分为非线性优化、预测—校正、人工势场法或启发式4类。在非线性优化方面,赵吉松等[5-9]基于配点法通过对控制、状态变量进行离散,构建出一种非光滑轨迹优化方法。周鼎等[10-13]利用考虑终端状态的伪谱法将连续最优控制问题转化为非线性规划问题,开展非致命故障下的任务降级轨迹规划问题研究。该方法具有性能最优、制导精度高的特点,但也存在强约束问题易收敛至局部最优解、优化时间较长的问题。在预测—校正方面,都延丽等[14-16]基于确定倾侧角翻转位置的航路点制导律,提出基于能量剖面的轨迹规划策略。在此基础上,章吉力[17]引入预测落点偏差作为目标函数进行指令求解,有效提升终端制导精度。此方法具备在线规划能力,但由于倾侧逻辑单一且不考虑能耗最优等指标,存在制导策略局限导致航程无法覆盖全部能力范围的问题。随着启发式概念的升温,空天飞行器轨迹设计逐渐智能化[18-19]。陈上上等[20-21]通过计算再入走廊边界的解析解,将约束转为对参考剖面剩余坐标限制的指标函数,完成采用粒子群优化的轨迹规划。但是粒子群优化只得到航迹剖面而非控制参数剖面,存在粒子数少于实际需求导致制导精度不足,轨迹无法物理实现的风险。
在轨迹跟踪制导律设计方面,李晓龙等[22-23]将高度回路转化为二阶无静差系统实现高度跟踪。在此基础上,刘凯等[24-26]应用期望极点配置完成轨迹误差时变反馈系统设计。但是基于经验设置的期望极点并不能保证二阶系统控制性能的全局适应性,上述方法不适用于动力学特性变化较大的全空域轨迹跟踪。
综上所述,考虑到现有方法在规划并跟踪有绕禁飞区需求、能量单调且冗余不足的升力式飞行器航迹时存在针对性不强的问题,提出飞行策略预划分手段,设计性能指标最优的多策略分段剖面函数。通过优化剖面飞行攻角、倾侧角剖面函数特征参数的方式将无穷维轨迹优化问题转化为有限维参数规划问题,完成多约束航迹规划。同时,基于LQR 调节器以位移加权误差最小为优化指标完成极点实时寻优的轨迹跟踪制导律二阶系统设计,从而满足全空域的高精度轨迹跟踪。最后,通过拉偏情况的仿真,证明了方法的有效性。
1 动力学建模与问题描述
1.1 质点动力学模型
质点动力学模型在弹道坐标系中建立,采用倾斜转弯模式(Bank To Turn,BTT),全再入过程均为无动力状态,在球形大地假设下给出三维质点动力学模型:
式中:V为速度;θ为弹道倾角;ψ为弹道偏角;h为高度;λ为飞行器在地表投影点的经度,ϕ为飞行器在地表投影点的纬度;Re为地球半径;g为重力加速度;m为飞行器的质量;γ为倾侧角;D为阻力;L为升力。
L和D的计算方法由式(2)给出:
式中:ρ为大气密度,可以视为高度的函数;Sref为参考面积;CL、CD分别为升力和阻力系数。
1.2 多约束航迹规划问题描述
多约束航迹规划是指在已知飞行器初始状态的情况下,设计满足末端状态和过程约束的攻角、倾侧角剖面,并为飞行器装订满足多种约束条件且性能指标函数最优的控制参数,从而完成优化设计的工作。已知初始状态和控制量为
为满足特殊的任务需求以及飞行器动力学特性,飞行全程将面临着严格的过程约束,如动压Qv、距离特定禁飞区最小斜距ΔRi等,具体可以描述为以下形式:
除此之外,为确保在中末制导交班点飞行器状态位于末制导窗口区间,需要设置如下的终端约束条件:
选用末速Vf最大作为性能指标,则多约束航迹规划问题可以转化为如下最优控制问题:
1.3 航迹跟踪制导问题描述
轨迹跟踪制导问题可以描述为对于给定的滑翔段标称轨迹:
利用线性二次型控制器设计原理,设计如下的状态反馈控制器:
状态反馈控制器基于设定的综合考虑制导控制偏差与偏差控制量积分的加权性能指标函数:
计算满足J最小的状态反馈控制器系数,使得飞行器能够用较小的加权偏差控制量确保实际飞行状态与跟踪标称飞行轨迹中装订值总的偏差加权值最小。其中:
则轨迹跟踪制导问题转化为如下的状态反馈控制器参数优化设计问题:
2 多约束飞行航迹优化设计
2.1 飞行策略剖面设计
针对现有方法(见表1)存在的计算量大、物理约束不满足问题,本文基于策略预划分手段分段设计策略剖面并优化参数,将无穷维轨迹优化问题转化为有限维参数规划问题,找到一条末速最优、又不违背各种约束的飞行轨迹,完成滑翔段强约束轨迹规划。滑翔段策略剖面分为纵平面、横侧向两部分,下面分阶段给出具体策略剖面设计方案。

表1 方法对比表Tab.1 Comparison of methods
2.1.1 纵向平面飞行策略方案
升力式飞行器滑翔段动力学特性差异明显,所以对某一固定单一的飞行策略剖面进行参数优化可能无法得到满足约束的全局最优、次最优解。针对这个问题,基于策略预划分手段将滑翔段分为3部分,分别为高空高速段、中空中速段和低空低速段,对应大攻角滑翔策略、定攻角策略和过渡段策略,通过分三段优化攻角剖面参数的方式完成纵向剖面设计。
在大攻角滑翔段,考虑到滑翔段初期飞行高度高导致大气密度低升重无法配平,为避免飞行器以较大的高度变化率下滑,轨迹整体高度过低导致航程缩减,过渡段采用固定大攻角下滑。弹道逐渐拉起后,待高度变化率为正后切换至定攻角飞行段。
在定攻角飞行段,考虑到该阶段飞行时间较长,设计复杂的攻角剖面形式存在优化时间过长的问题,所以采用定攻角模式飞行,幅值以末速最大为优化指标获得,当弹目相对距离Dr小于预设值Dr0后切换至过渡段。
在过渡段,考虑到中末制导交班点存在严格的高度、速度和弹道倾角约束,简化的定攻角优化方式并不适用,所以采用多项式剖面。但为减小优化维数,结合升阻系数计算方式(2),将攻角形式设置为与速度相关的函数。在此基础上,引入弹目距离Dr倒数为自变量的修正项,从而在弹目距离足够小时对攻角进行微调,确保终端条件得到满足。
综上,攻角剖面可以表示为以下形式:
式中:α1、α2、a3、a4为待优化参数;C1为初始值为0的标志位,若θ≥0°则恒为1。
飞行器首先由于C1默认为0 且Dr>Dr0执行α1指 令;当C1变 为1 且Dr>Dr0时执行α2指令,当Dr≤Dr0后执行α(V Dr)指令,攻角剖面如图1所示。

图1 攻角剖面Fig.1 Sketch of the attack angle section
2.1.2 横侧向平面飞行策略方案
由于制造业企业所得税结构受各国税制结构因素的影响,因而制造业企业在税基设置、税率水平、税前扣除、税收优惠等方面也迥然不同。
横侧向平面策略函数优化倾侧角剖面γ(t DrΔRi)。首先,为确保滑翔段末段弹道偏角满足约束,设计自变量为弹目距离的弹道偏角过渡函数γc,通过平滑过渡的方式将弹道偏角转至期望值ψf,确保在滑翔段末段弹道偏角满足约束。
除此之外,为与禁飞区保持一定距离,设置了自变量为导弹与禁飞区斜距倒数的斥力场函数。当相对距离小于预设值ΔRimin后加入修正指令Δγ,确保不会进入禁飞区。
式中:b1、b2、b3、bi为待优化参数。
2.2 非线性参数规划算法
考虑只含有等式约束条件的非线性规划问题:
式中:c(x)为向量函数c(x)={c1(x),c2(x),…,cm(x)}T。
则拉格朗日函数为
可写成如下形式:
若矩阵Bk是Hessian 矩阵L(xk,λk)的良好近似,则下式成为拟牛顿法的迭代公式:
上述的SQP 法,理论上只具有局部收敛性,为使其具有整体收敛性,则:
具体算法流程如图2 所示:

图2 SQP 程序框图Fig.2 Program chart of the SPQ algorithm
3 轨迹跟踪制导律设计
将高度H、射击系z项位移影响作为关注状态量,引入位移微分项对状态方程扩维,沿飞行轨迹线性化可得:
描述为状态空间形式为
考虑飞行过程中与标称轨迹的偏差,沿着e(t)=0,(t)=0 进行线性化可以得到
针对线性化后的时变系统,这里需要设计一个状态反馈控制器:
通过线性二次型调节器配置反馈矩阵K,找到一组控制量u(t)。假设ATP+PA+Q+KTRK-KTBTP-PBK存在一个常量矩阵P使得:
令K=R-1BTP,则:
在此基础上,通过求解黎卡提方程得到矩阵P与控制参数K,轨迹跟踪制导律为以下形式:
4 仿真分析
4.1 仿真输入
假设飞行器初始点经纬度为(0.0°,0.0°),计划绕过经纬度为(4.7°,0.5°)、经纬度为(6.7°,0.7°)的两个半径为50 km 的禁飞区,并到达距离经纬度为(11.3°,1.0°)的目标点航程90 km 的中末制导交班点。结合上述情况,初始状态见表2。
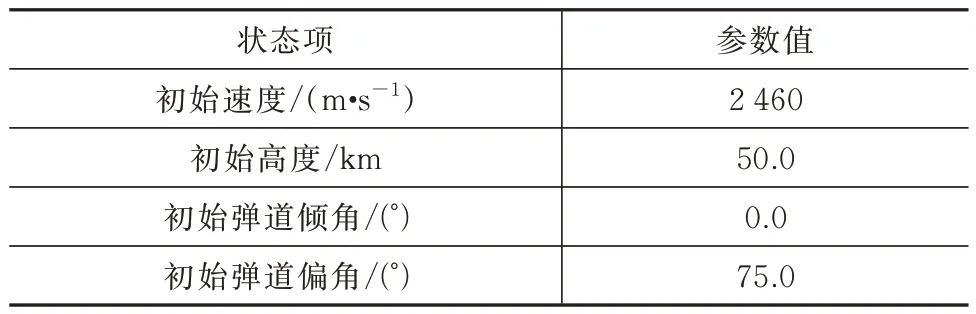
表2 初始状态信息表Tab.2 Initial state information
这里设置如表3~表4 的过程、终端约束,以末速最大为优化指标,优化满足所有约束的滑翔段轨迹。
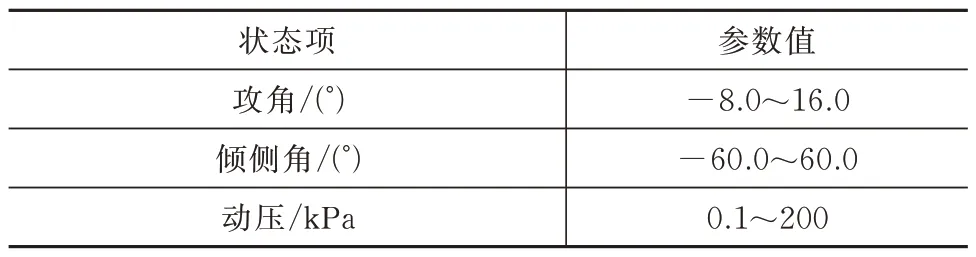
表3 过程约束信息表Tab.3 Process constraint information

表4 终端约束信息表Tab.4 Terminal constraint information
4.2 轨迹优化仿真分析
滑翔轨迹如图3 所示,由图3 可知,飞行器能够飞抵中末制导交班点,且能够与上述禁飞区保持安全距离。

图3 滑翔轨迹Fig.3 Gliding trajectory diagram
速度、高度-时间曲线如图4 和图5 所示,由图4和图5 可知,采用非线性参数优化算法飞行时间约为470 s,最大高度为初始点的50 km,末速为1 406 m/s。考虑到末速为本次优化指标,利用全局优化算法进行指标检验,在此基础上开展两者的优化计算效率对比分析。非线性参数规划算法(470 s,1 406 m/s)相较于优化算法(463 s,1 412 m/s)末速减小0.4%,但是优化时间由原有162 s 减小为70 s,提升131.4%。

图4 速度-时间曲线Fig.4 Speed-time curve

图5 高度-时间曲线Fig.5 Height-time curve
弹道倾角-时间曲线如图6 所示,由图6 可知,标称轨迹的终端弹道倾角为-3°位于终端约束范围内,飞行器状态满足中末制导交班条件。

图6 弹道倾角-时间曲线Fig.6 Trajectory inclination angle-time curve

图7 弹道偏角-时间曲线Fig.7 Trajectory declination angle-time curve
4.3 轨迹跟踪仿真分析
考虑气动不确定性的轨迹跟踪仿真分析,验证TLC 算法是否具有稳定跟踪标称弹道的能力。功角、倾侧角-时间曲线如图8 和图9 所示,由图8 和图9 可知,在升力系数10%、阻力系数20%偏差的情况下,TLC 算法能够基于当前时刻的位置、速度偏差解算修正指令,使得跟踪误差不发散。

图8 攻角-时间曲线Fig.8 Attack angle-time curve

图9 倾侧角-时间曲线Fig.9 Pitch angle-time curve
高度误差、Z向位置误差如图10 和图11 所示,由图10 和图11 可知,飞行器在拉偏情况下,实际轨迹与标称轨迹Y、Z轴误差全程均小于0.1 km,基于TLC 算法得到修正指令后能够稳定跟踪原有轨迹,从而确保飞行器精确到达中末制导交班点。
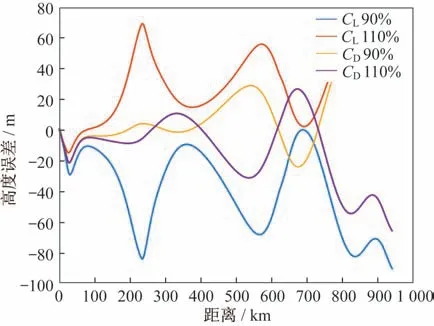
图10 高度误差-时间曲线Fig.10 Height error-time curve

图11 Z 向位置误差Fig.11 Position error along the Z-axis
5 结束语
本文针对升力式飞行器滑翔段多约束航迹规划问题,首先结合飞行器不同空域的任务需求及弹道特性,基于飞行策略预划分手段提出针对不同飞行状态的攻角、倾侧角分段剖面函数。在此基础上,利用序列二次规划方法通过优化满足过程、终端约束的剖面函数特征参数的方式,得到性能指标函数最优的控制构型剖面,从而完成多约束航迹规划。最后,通过线性二次型控调节器实时解算位移误差加权值最小的状态跟踪反馈控制器系数,完成考虑气动不确定性的轨迹跟踪制导律设计,从而为升力式飞行器多约束航迹规划方案提供具备工程实用价值的技术途径。
