几何结构对S-CO2离心压缩机热力学性能影响分析
2024-01-08赵富龙田游游田瑞峰胡朝营刘凯
赵富龙, 田游游, 田瑞峰, 胡朝营, 刘凯
(1.哈尔滨工程大学 核科学与技术学院,黑龙江 哈尔滨 150001; 2.黑龙江省核动力装置性能与设备重点实验室,黑龙江 哈尔滨 150001; 3.中车株洲电机有限公司,湖南 株洲 412000)
在核能利用方式上,采用S-CO2布雷顿循环在循环效率、设备紧凑性、结构复杂度等方面均有明显优势,因此布雷顿循环在未来能源转化利用方向上有广阔的前景[1]。压缩机是S-CO2布雷顿循环的核心部件,对于发电功率小于50 MW的S-CO2发电循环,循环系统可以选用单级或多级离心压缩机[2-3]。对于小型S-CO2布雷顿循环,离心压缩机由于具有较大的稳定工作区间,有着广泛的应用。在整个布雷顿循环系统中,离心压缩机对S-CO2做功,以提高S-CO2的循环压力,保证布雷顿循环系统的正常运行[4-5]。
在离心压缩机设计阶段,需要考虑到众多几何参数对其性能的影响,例如叶片数、叶顶间隙、叶片后弯角、分流叶片长度、无叶扩压器长度等几何参数。Lettieri等[6]发现使用有叶扩压器可以提高低速度系数的S-CO2离心压缩机的效率。Monje等[7]研究了S-CO2压缩机的设计方法,阐释了如何选择一维设计参数,介绍了多维设计方法,在S-CO2压缩机设计中采用了锥形扩压器,研究了锥形扩压器在不同工质下(空气和S-CO2)的气动性优劣。Behafarid等[8]设计了3种一维模型,模型之间的区别在于采用的物性不同,分别为理想状态、可压缩、不可压缩物性,通过直接数值模拟对3种模型结构进行了数值计算,发现一维模型的精确性对可压缩与不可压缩这2种物性并不敏感,而理想气体物性带来了较大的误差。Kim等[9]对S-CO2离心压缩机整机(包括扩压器和蜗壳结构)进行了计算流体力学模拟,发现运行工况点远离S-CO2临界点时使用SSTk-ω湍流模型计算比较准确,当压缩机进口工况在临界点附近时,数值模拟误差会变大。Pecnik等[10]以Sandia实验室的S-CO2主压缩机为原型,开展了稳态下的性能计算分析,发现超S-CO2压缩机进口工况靠近临界点时,容易产生跨临界流动。Budinis等[11]对S-CO2离心压缩机的控制系统进行了设计与分析,提出了评估压缩系统的控制性能和功耗的性能指标,比较了亚临界压缩和超临界压缩在离心压缩机防喘振过程中的影响。美国Sandia实验室[12-13]、日本东京工业大学[14-16]、韩国原子能研究所[17]和中国科学院工程热物理研究所[2]均公开了S-CO2布雷顿循环系统中离心压缩机的相关设计参数和试验结果,其他研究机构也对不同功率级的S-CO2离心压缩机内部流场、变工况特性等开展了很多机理性的研究[18-20],针对某一种几何结构的研究较多,但对多种结构对S-CO2离心压缩机性能影响研究并不全面。
本文对某S-CO2离心压缩机从叶片数、叶顶间隙、叶片后弯角、分流叶片长度、无叶扩压器长度几个较典型的结构特征着手,采用控制变量法,通过每次只改变一种结构参数,分析它们各自对S-CO2离心压缩机的热力性能的影响。利用了线性加权和法[21]对每种结构下的离心压缩机性能进行了定量评价。
1 S-CO2离心压缩机模型与数值方法
1.1 S-CO2离心压缩机几何模型
本文对某MW级S-CO2离心压缩机进行了一维和三维建模,子午面如图1所示,该离心压缩机由叶轮和无叶扩压器组成。叶轮叶顶间隙布置方式为常数控制法,叶轮叶片数为带分流叶片8+8形式。该离心压缩机设计参数为:进口压力8.15 MPa,进口温度308 K,流量135 kg/s,转速20 000π rad/min,压比1.9。该兆瓦级原型压缩机几何结构参数如表1所示,几何造型如图2所示。

表1 S-CO2离心压缩机设计参数Table 1 Design parameters of S-CO2 centrifugal compressor

图2 S-CO2离心压缩机几何造型Fig.2 S-CO2 centrifugal compressor geometric modeling
1.2 数值方法
1.2.1 三维CFD求解方法
本文采用数值方法求解三维定常Navier-Stokes方程。空间离散采用二阶中心格式,湍流模型采用SSTk-ω模型,动静交界面采用混合平面法,边界条件采用压力进口流量出口边界。对出口温度与进出口流量比进行监测,当监测点变化幅度小于0.5%时,即可认为达到收敛,其计算结果可信。由于超临界二氧化碳物性的特殊性与离心压缩机内存在强烈的逆压梯度,直接求解会导致计算稳定性很差,所以需要在正式求解之前选择一个合适的初场,该初场在额定工况的基础上,适当缩小后计算可得。求解速度的快慢与时间尺度因子关系较大。时间步长为自动时间步长与时间尺度因子之积,自动时间步长由算法自动选取,只有时间尺度因子需要进行控制。时间尺度因子越大,收敛速度越快,但会带来计算不稳定的缺点,本文时间尺度因子在1~10选择。
1.2.2 线性加权和法
压比和效率是离心压缩机的2个关键性能指标,关于离心压缩机的性能评价与选择需要权衡这2个方面的优劣。分析多目标优化问题时由于最终只需要一个最优解,故通常将多目标问题转化为单目标问题,引入一个评价函数即可实现,利用线性加权和法构建性能评价函数。由于指标数只有2个,使用最常用的标准离差法进行权重确定,各指标的权重为[21]:
(1)
式中:n为指标数;ωi为第i个指标的权重;σi为第i个指标的标准差。
压缩机的性能评价函数为[16]:
γ=ω1ε′+ω2η′
(2)
式中:ω1和ω2分别为压比和效率的权重;ε′=(εi-εmin)/(εmax-εmin),εmin为压比最小值,εmax为压比最大值;η′=(ηi-ηmin)/(ηmax-ηmin),ηmin为效率最小值,ηmax为效率最大值。
1.3 网格无关性验证
S-CO2离心压缩机三维CFD计算网格如图3所示,由于结构对称,为节省计算资源,采用单流道进行计算。当第1层网格厚度约为1.5时足以满足计算需要,因此本文后续所有网格的划分都依照第1层壁面网格厚度1.5的标准[22]。在此基础上对S-CO2离心压缩机进行网格无关性验证,在保证计算准确性的同时降低计算成本,以得到最佳网格数。表2为不同网格数下压缩机的总压比和效率,可以看到,当网格数在165万时,网格数对总压比和效率的影响已降到较小水平,综合考虑计算成本和精确度,最终选择165万网格数进行后续计算。

表2 网格无关性验证Table 2 Grid independence verification

图3 S-CO2离心压缩机单流道三维CFD计算网格Fig.3 Single channel 3-D CFD computational grid of S-CO2 centrifugal compressor
2 S-CO2离心压缩机数值模拟与性能分析
2.1 几何结构选取
本文在1.1节中所设计的兆瓦级S-CO2离心压缩机设计基础上,从叶片数、叶顶间隙、叶片后弯角、分流叶片长度、无叶扩压器长度这几个较典型的压缩机结构特征参数着手,采用控制变量法,每次只改变一种结构参数,分析对S-CO2离心压缩机的性能的影响。
2.2 原型压缩机流动状态
图4为50%叶高处B2B截面的流动参数分布。B2B截面为流道展向截面,叶片表面压力分布曲线中,每条封闭曲线代表一个叶片,其中较短的封闭曲线为分流叶片,每条封闭曲线的上半部分表示压力面,下半部分代表吸力面,两者的差值为叶片所受到的载荷。在主叶片进口前缘处存在较小的冲角,冲角的存在造成了进口前缘吸力面与压力面压力和温度的不同分布,分流叶片进口前缘处由于上游流道的约束性,流体流动比较稳定,冲角小于主叶片处,故主叶片进口冲击载荷要大于分流叶片。由于尾缘的处理方式为直接铣削,厚度较大,故能在尾缘处观察到明显的射流-尾迹结构[23]。流道内压力和温度的主要升高区域在叶轮后半段和扩压器段,熵增主要出现在流道尾部的叶片吸力面、无叶扩压器中来自上游的尾迹区和进口前缘吸力面。

图4 50%叶高处B2B截面的流动参数分布Fig.4 The flow parameter distribution of B2B section at 50% blade height
2.3 不同结构对性能影响分析
图5(a)为额定工况下不同叶片数的S-CO2离心压缩机性能变化曲线。随着叶片数的增加,叶轮做功能力逐渐增强,压缩机压比增加。压缩机效率在14~16叶片区间附近达到极大值,12和18叶片效率均有所下降。以上压缩机特性的出现与轴向涡流有关,轴向涡流的存在使实际流动出口角小于叶片的后弯角,进一步造成出口绝对速度的切向分速度的减小,因此压比减小。叶片数的增加有利于抑制轴向涡流,故压比随叶片数增加而增加,但摩擦损失的增加和可能发生的堵塞,造成了18叶片数下的效率下降。
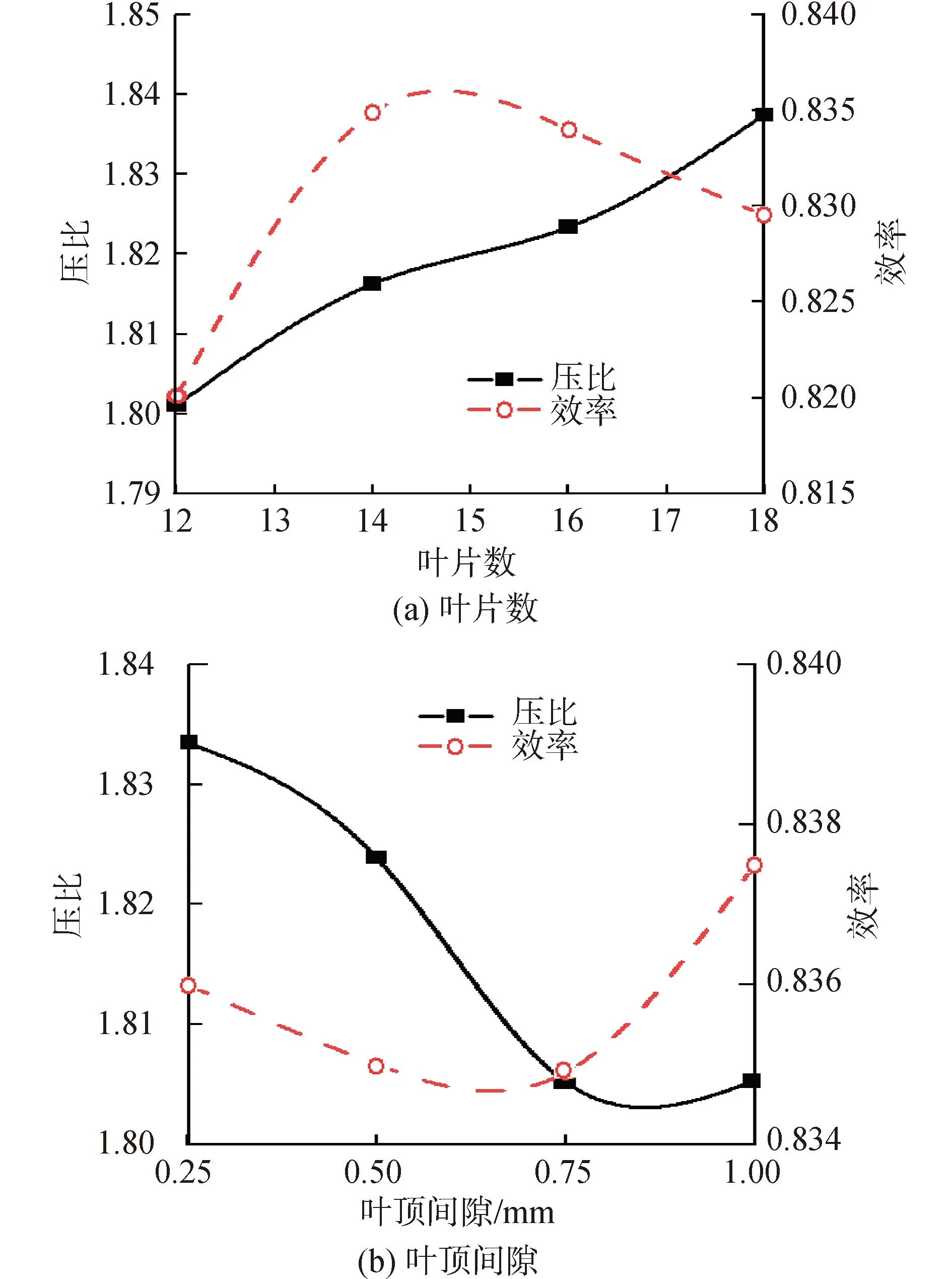

图5 不同结构下离心压缩机性能变化曲线Fig.5 The performance change curves of centrifugal compressor under different structures
图5(b)为不同叶顶间隙下离心压缩机性能变化曲线。从整体上来看,叶顶间隙对压缩机的压比影响最大。叶轮的效率是总焓增与叶轮消耗功的比值。叶顶间隙的增大对压比的提高起负增益效果,但当间隙不小于0.75 mm,后压比基本不变;在0.25~0.75 mm内,叶顶间隙增大后效率随叶顶间隙的增大而减小,但叶顶间隙为1 mm时效率有小幅提升。经计算,叶顶间隙变化造成的压比相对变化量为1.6%,造成的效率相对变化量为0.6%,显然压比对叶顶间隙的敏感性更强。在0.75 mm间隙以下时,叶顶间隙增大使压比和效率同时下降,所以尽量小的叶顶间隙一直是离心压缩机的设计目标之一,这也能解释相同参数下闭式叶轮比半开式叶轮效率高。
图5(c)为不同叶片后弯角下的离心压缩机性能变化曲线。随着后弯角的增加,压缩机压比减小,叶轮做功能力逐渐减弱。增加后弯角对出口速度三角形的影响效果与轴向涡流带来的影响效果等效,当后弯角增大时,相对出口速度向右滑移,使绝对出口速度的切向分速度减小,叶轮做功能力会减弱,造成压比的降低。压缩机效率在后弯角-40°附近达到极小值,在此基础上,减小或增大后弯角叶片效率均会有所增加,增大后弯角对效率的增益更大。总体上在合理范围内大后弯角下的压缩机效率更高,后弯角增大后,相对出口速度向右滑移,使绝对出口速度减小,出口动能的减小意味着总耗功中用于提高流体压力的耗功增大,即叶轮效率会提高;另一方面,后弯角增大后流体相对出口速度的滑移使流体在无叶扩压器中的绝对速度气流角增大,缩短了流体在无叶扩压器中的流程,减小了摩擦损失,这意味着无叶扩压器效率的提高。综合后可以得到大后弯角下的压缩机效率更高的结论。
图5(d)为不同分流叶片长度系数下离心压缩机性能变化曲线。当分流叶片长度从较小水平增加到较大水平的过程中,压缩机的压比和效率的变化表现出一致性,均在分流叶片长度为0.74处达到极大值。增加分流叶片的长度有助于改善压缩机内的流场,但过长的叶片也会带来流动堵塞问题和更大的摩擦损失。
图5(e)为不同无叶扩压器长度下离心压缩机性能变化曲线。当无叶扩压器长度增加后,离心压缩机的总对静压比在无叶扩压器长度系数1.4~1.6时迅速增大,大于1.6之后增速减缓。离心压缩机效率也随无叶扩压器的长度的增加而提高,且当无叶扩压器长度系数为1.2时,效率远低于其他结构。因为扩压器中流程太短,流体来不及进行减速扩压,更多的能量以动能的形式被带走浪费而没有变成设计预期的总对静压比的提升。总体上无叶扩压器增加长度不仅可以提高有效压比,还能提高效率,因此在适当范围内提高无叶扩压器长度有利于离心压缩机性能的提高。
从表3中可以看到,随着叶片数的增加,离心压缩机的性能值逐渐提高,因为压比所占的权重值更大,且随叶片数的增加效率变化率小于压比变化率,综合影响下叶片数越多性能值越大;随着叶顶间隙的增加,总体上离心压缩机的性能值在下降。间隙越小越有利于压比的提高,由于压比在性能评估中占比很大,就造成性能值随叶顶间隙的增加而减小的现象;后弯角增大后压比在大幅减小,即使叠加上效率增加的影响后性能值依然无法弥补地下降,总体上性能值随叶片后弯角的增大而减小;在分流叶片长度为0.74时,压比和效率均为4种结构中的最优值,性能值达到最大值1。当分流叶片长度继续小幅增大时,性能会有所下降,分流叶片长度减小为0.6时,压缩机性能值下降明显,仅为0.108 8。综合评判下分流叶片长度0.74左右下的压缩机具有最优性能;当无叶扩压器长度系数为1.7时,压比、效率和性能值均为4种结构中的最大值;当长度系数为1.2时,效率相较于压比下降更为明显,离心压缩机性能最差。由于叶轮处结构完全一样,4种结构的差距主要来自于无叶扩压器段,较大的无叶扩压器长度系数能有效改善扩压器内的流场,提高离心压缩机整机的性能。

表3 不同结构下离心压缩机样本数据
2.4 几何敏感性分析
表4对5种不同结构下离心压缩机压比和效率变化量进行了总结,图6为5种不同结构下离心压缩机压比和效率相对变化量。叶片后弯角的变化对离心压缩机的压比和效率同时造成较大的影响,效率对无叶扩压器长度的变化十分敏感。压比对各个结构变化的敏感性排序:叶片后弯角>无叶扩压器长度>叶片数>叶顶间隙>分流叶片长度;效率对各个结构变化的敏感性排序:无叶扩压器长度>叶片后弯角>分流叶片长度>叶片数>叶顶间隙。可见叶片后弯角和无叶扩压器长度对离心压缩机压比和效率的影响最大,在设计时要优先考虑这2种结构对离心压缩机性能的影响。
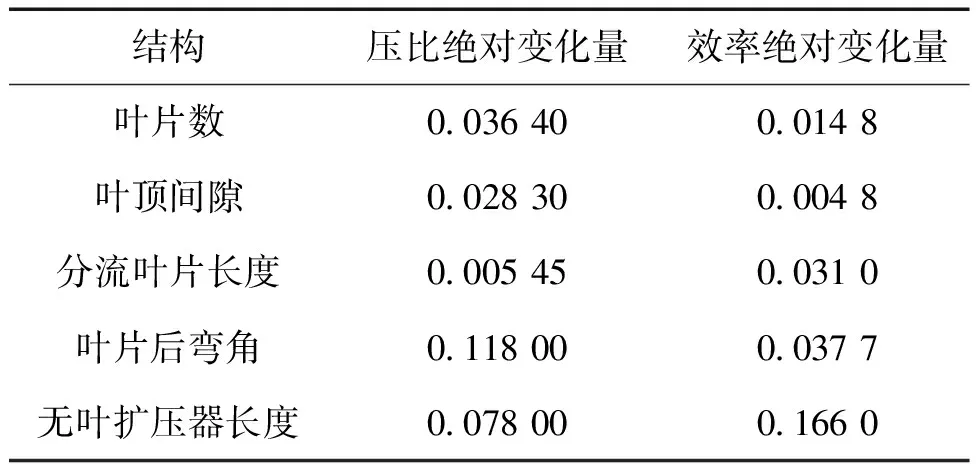
表4 性能参数的均值和方差计算误差
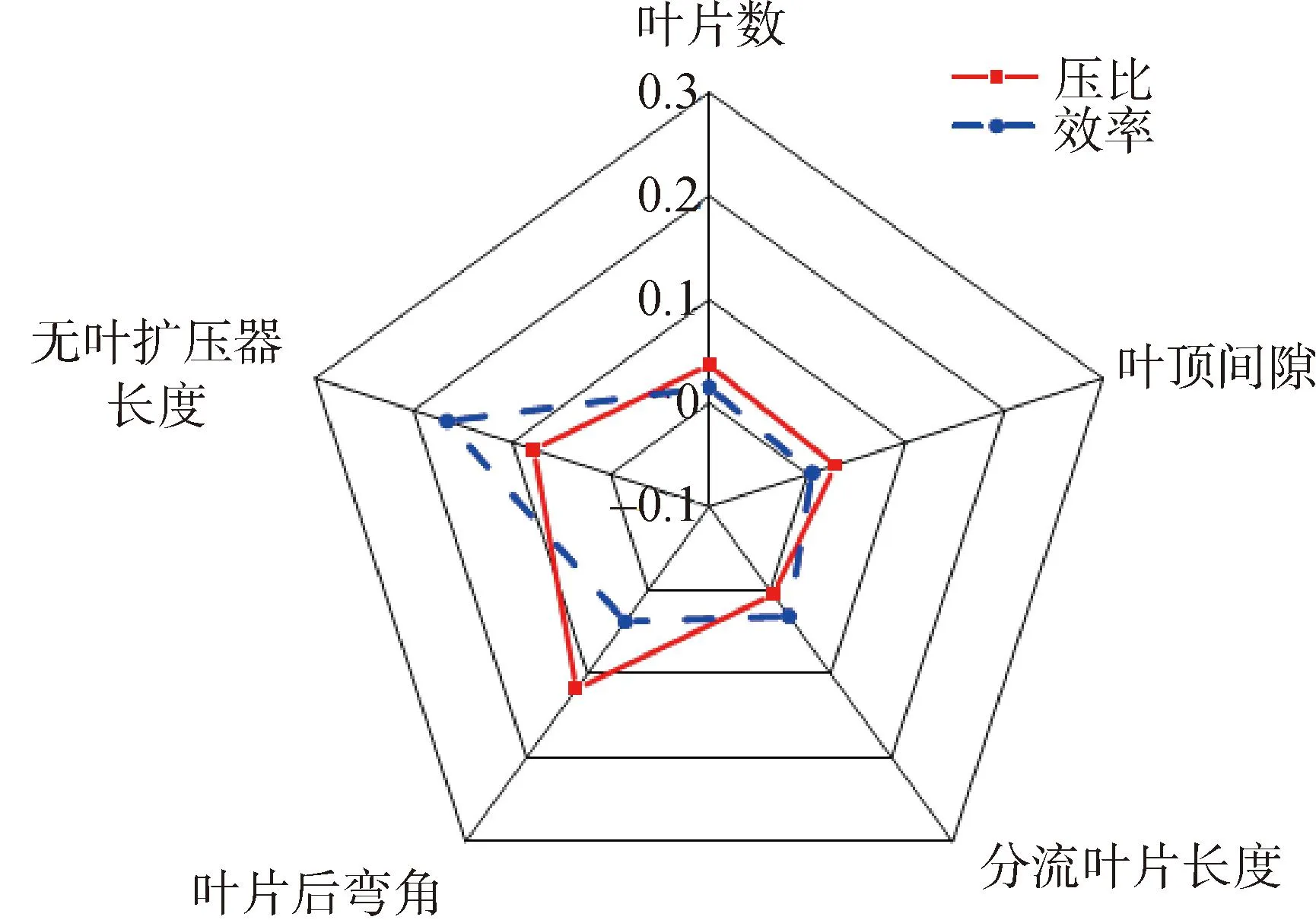
图6 不同结构下压比和效率变化百分比Fig.6 The percentage change of pressure ratio and efficiency under different structures
3 结论
1) 叶片数增加可提高叶轮做功能力和压比,但过多会降低效率;叶顶间隙应在强度和裕量允许的前提下尽量取较小值;本文中最佳分流叶片长度系数为0.74。
2) 叶片后弯角对离心压缩机压比和效率影响较大,后弯角的增大会降低叶轮做功能力从而降低压比,但大后弯角有利于离心压缩机效率的提高;无叶扩压器长度也存在一个最优值,在本文的计算工况中,无叶扩压器越长对离心压缩机的性能提高越有利。
3) 通过分析5种结构下离心压缩机压比和效率的相对变化量,发现叶片后弯角和无叶扩压器长度对离心压缩机性能影响最大,其次是叶片数、分流叶片长度和叶顶间隙,因此在进行离心压缩机设计时应优先考虑叶片后弯角和无叶扩压器长度。
