数形结合思想在中职数学教学中的应用探析

何平

【摘要】客观世界是一个相互关联的整体，事物之间通过各种方式相互依赖、作用和制约.在数学研究中，数与形是两类基本对象，同样遵循这一原则.在中职数学教学中，教师可以将某些数量关系问题和图形性质问题建立密切联系，以达到“形”助“数”或以“数”赋“形”的目的.数形结合的实质就是通过一定的方式将直观的图形与抽象的数学符号联系起来，进而在形象思维和抽象思维之间建立沟通交流的桥梁.这样，通过使用直观的图形，学生能够更好地理解抽象概念，并将其与具体的形象和表达方式联系起来.这种方法使得原本复杂的问题变得简单易懂，烦琐的计算变得简洁明了.基于此，文章结合以往的教学经历，以中职数学教学为载体，将数形结合思想在教学中的应用展开研究分析，以期能够为教育从业者提供借鉴参考.

【关键词】数形结合思想；中职数学；数学教学

引 言

对于中职学生来说，数学教学活动的开展会对学生的理性思维能力的培养具有推动作用.针对现有中职数学教学形式而言，教育工作者的追求一直都是致力于探讨如何有效开展中职数学教育.笔者认为，在研究中融入数形结合思想将会对中职教育具有十分积极的影响，不仅能提升学生解题的效率，还能培养他们的数学思维能力.在如今素质教育的大力推广下，学校不再将重点放在成绩上，而是将学生综合能力的培养放到更重要的位置上.因此，当前如何借助数形结合思想提升教师的教学质量和学生的学习效果成为很多教师重点关注的问题.

一、数形结合思想的内涵介绍

数形结合思想是一种在数学教学中广泛应用的方法，旨在通过将数学概念与几何图形相结合，促进学生对数学知识的理解和应用.数形结合思想强调数与形的统一，即通过观察几何图形的特征和性质，揭示其中蕴含的数学规律和关系.这种思想将抽象的数学概念转化为具体的可视化形象，以提高学生的学习兴趣和理解能力.数形结合思想的内涵主要包括以下几个方面：

（1）数形结合思想追求数学与几何的有机融合.传统的数学教学往往将数学抽象地呈现给学生，导致学生难以理解和应用.而数形结合思想通过将数学概念与几何图形联系起来，使学生能够直观地观察和感受数学规律，加深对抽象概念的理解.（2）数形结合思想注重培养学生的空间想象力和几何思维能力.通过观察几何图形的形状、大小、位置等属性，学生可以锻炼自己的空间想象力，提高解决几何问题的能力.同时，数形结合思想也鼓励学生进行推理和证明，培养他们的几何思维能力.（3）数形结合思想强调实际问题与几何图形的联系.在数学学习中，学生经常会遇到与实际问题相关的几何图形，如建筑、地图等.数形结合思想通过将这些实际问题与数学概念相结合，使学生能够将抽象的数学知识应用于实际生活中，加深学生对数学的认识和兴趣.（4）数形结合思想还注重激发学生的创造力和探索精神.通过观察和研究几何图形的规律，学生可以主动探索和发现数学知识，培养自己独立思考和解决问题的能力.总体而言，数形结合思想是一种将数学与几何相结合的教学方法，通过数与形的结合，更清楚地向学生揭示其中所蕴含的规律，从根本上提升学生对于数学的理解，并在不断积累中提升学生学习数学的兴趣.

二、数形结合思想在中职数学中的应用优势分析

（一）数形结合思想适用于中职数学的内容

对于数学学科教學来说，数形结合思想具有广泛的适用性.数学作为一门抽象性较强的学科，在传统的教学模式中，常常被理解为纯粹的符号运算.然而，数形结合的思想通过将数学与几何图形相结合，能够将抽象的数学概念具象化，使学生更容易理解和掌握相关知识.例如，在解决实际问题时，学生常常需要利用图形进行建模和分析.通过数形结合的思想，学生可以将数学概念与具体的图形相联系，进而更好地理解问题的本质和解题方法.此外，数形结合能够拓宽学生对数学知识的认知范围，将数学与几何、统计等学科进行整合，促进学生跨学科的思维发展.

（二）数形结合的思想可以激发学生的学习兴趣

在中职数学教学中，作为教育者，我们可以发现很多学生对数学常常存在一定的抵触情绪，认为数学难以理解和应用，从而有很多学生在课堂上无精打采，对学习提不起兴趣.而数形结合思想能够通过图形的直观表达激发学生的学习兴趣，使学习过程变得更加有趣和具有挑战性.借助数形结合思想，学生可以通过观察、探索和实践，感受数学的实用性.在几何学习中，学生可以通过绘制几何图形来发现形状之间的规律与联系，从而培养对几何学的兴趣和好奇心.此外，教师还可以引入一些趣味性的活动和游戏，如立体图形的分解，借助游戏的形式开展数学教学活动可以有效激发学生主动参与和提高学生的学习动力.

（三）数形结合思想可以提高学生的思维能力

众所周知，数学教学的目的并不是机械呆板地向学生传达数学符号之间的关系，然后让学生死记硬背，数学教学更重要的是培养学生的数学思维能力.而数形结合思想能够使学生对事物进行仔细观察、认真分析和具有针对性的推理，从而提高他们的逻辑思维和问题解决能力.通过数形结合的思想，学生需要将抽象的数学概念转化为具体的图形表达，而直观的图形关系也可以借助数学符号表达出来.在这个过程中，学生需要运用空间想象、几何推理等多种思维方式进行思考.学生在解决一个几何问题时，他们需要观察图形特征、辨别形状属性，并据此进行逻辑推理和证明.这样的思维活动对于培养学生的综合思维和创新思维具有积极的促进作用.

（四）数学结合思想可以让学生轻松记忆知识点

在中职数学学习中，学生需要掌握大量的数学知识点和公式.然而，传统的死记硬背方式常常使学生感到厌烦和困惑.而数形结合的思想可以通过图形和模型的视觉呈现，帮助学生更轻松地记忆和理解相关知识.数形结合思想通过将抽象的数学符号与图形相结合，使学生能够通过直观的图像记忆理解相关的知识点.在学习平面几何的定理时，学生不再感觉枯燥，学生可以借助图形的特征和位置关系来记忆定理的内容和证明方法.这样的视觉记忆不仅使学生能够更好地理解知识，还能够提高他们对知识点的准确性和记忆的持久性，进而从源头上达到对数学学习改观的目的.

三、数形结合思想在中职数学中的具体应用分析

（一）数形结合思想的应用：解决椭圆与直线相交求最小值的问题

通过对数学教学实践的观察可知，我们通常需要将一些几何问题转化为数量关系图形来进行解答.几何图形虽然具有鲜明的直观性，但还是需要借助于数量关系进行表达.所以，在教学实践中，数形结合思想是学生学好数学所必须要掌握的思维能力.学生通过数形结合思想才能在问题解决中主动寻找数量关系，从而更精确地定位图形并成功解决问题.而对于教师来说，在教学中应重视研究将图形转化为数量关系的教学方法，引导学生认识图形的几何特性和表达方式.学生将直观的几何图形用数量关系进行表达需要掌握相关步骤，并能从中提取出重要的信息.同时，学生也能在这个转换过程中深入理解问题的关键所在，并更好地处理好数学问题.数形结合思想可以有效拓宽学生的解题思路，使学生在面对问题时，不易遗漏核心信息，并提高数学学习的效率.比如，在解决椭圆与直线相交求最小值的问题时，教师在具体讲解过程中就可以引导学生先找出问题中不易发现的隐藏条件，接着就是在数形结合思想的指引下用文字数量关系定位图形.按照这个思路，学生通过观察几何图形，就能够将图形转化为数字的形式，从而成功解决问题.这种通过数量关系解决几何图形问题的方法，在不断的练习培养中可以帮助学生更好地把握数量背后的关系，进而与图形特征建立对应关系.数与形的结合，有效达到了简化问题和提高数学解题效率的目的.同时，对于学生的学习经验积累来说，不断运用数形结合思想还在潜移默化中提升了学生的形象意识、思维意识，为学习质量的进一步提升提供了必要的助推.

（二）数形结合思想的应用：解决集合的相关问题

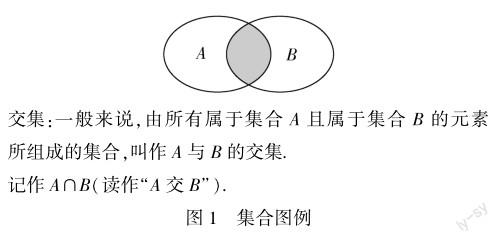
教师在进行数形结合教学时，应注重培养学生的抽象意识，帮助他们将抽象的数字转化为具体的图形.虽然数学与现实密切相关，但其中有些概念还是十分抽象的，对学生来说可能难以理解.过于抽象的概念往往会使学生感到困惑，难以深入领会教师所传授的知识.因此，数形结合思想可以帮助学生提高抽象思维能力，更好地掌握数学知识.比如，在讲解集合这一章节的内容时，教师可以运用数形结合的方法帮助学生理解交集和并集的概念.在教学实践中，教师可以先用多媒体展示出两个圆分别代表两个集合，紧接着再以动图的形式向学生展示两个圆相交的轨迹，最终呈现如图1所示.通过这样的方式学生就能够更直观地理解数学符合所表达的意义，并加深对集合概念的认识.在学生充分理解了这些概念后，再解决复杂的集合计算题时，教师可以引导他们运用这种图形化方法来解题.学生可以在草稿纸上自行绘制和计算集合，这样的解题过程既清晰又直观，能够大大提高解题效率.通过数形结合思想的应用，学生能够更好地理解抽象的数学概念，使得学习过程更加有趣.此外，教师还可以鼓励学生观察和分析其他类型的问题，将其转化为具体的数量关系或几何图形，以便更好地解决问题.所以，对于教师而言，应当引导学生将抽象的概念转化为具体的图形，帮助他们更好地理解、掌握数学知识，进而可以使他们在解决问题时进行直观的思考，并且能够更快速地找到解题的方法和答案.

四、數形结合思想在中职数学中具体应用时的关键点

（一）着重培养学生的数形转换意识

对于中职数学中教师的教学过程和学生的学习过程来说，采用数形结合的方式或采用形式化的方式解决问题，并不是只要能进行简单的互相转换就算达到目的，而是需要针对问题的实际情况引导学生进行深入分析，在实践中培养学生遇数寻形、见形思数的解题意识.例如，在解决取值范围和最小值类型的习题时，教师应该将数形结合思想融入教学中，引导学生探究数量与几何图形之间的联系，通过比较二者的特点，从多个角度来思考问题，从而简化题目难度，使学生能够在更加清晰明了的解题途径中，快速地解决问题.通过不断的实践练习，学生才能逐渐提升自己在解决数学问题时的联想意识，实现图与形之间的相互转换，最终求得答案.

（二）重视学生思维灵活性的培养

在中职数学教育中，重视培养学生的思维灵活性是非常关键的.其中，有针对性地在教师的教学中和学生的学习中引入数形结合思想是一个十分可行且有效的方法.通过掌握数形结合思想，学生可以在解题困境中转变思维方式.这种思维角度的转变不仅在解数学题时有效，而且对于学生未来可能面临的各种难题也具有一定的帮助.因此，在日常的教学过程中，教师应该向学生传达数形结合思想的重要性，还应积极思考如何更好地将数形结合思想融入数学教学.笔者相信，通过师生之间的密切配合，学生的逻辑思维能力、解题灵活性都能够得到进一步的提升，进而构建出一个高效的课堂环境，使学生的学习效率和教师的教学质量都能得到质的飞跃.

结 语

综上而言，随着素质教育的大力推行，教育制度也在进行不断的完善和改进，教育事业在发展中实现了较大的进步.所以，中职院校数学教学也不能忽视自身的教学要求，应与时俱进地不断实现自我提升和创新.教师们可以通过数形结合的方法，引导学生掌握数学学习中概念知识与几何图形之间的联系，培养他们的解题能力和思维能力，进而提高学生的综合素养.

【参考文献】

[1]宋金平.以形辅数以数带形———数形结合思想在中职数学教学中的渗透与应用[J].数学学习与研究，2022（24）：17-19.

[2]郭凤艳.数形结合思想在中职数学教学中的应用[J].发明与创新（职业教育），2019（2）：28.

[3]殷环洲.巧用数形结合，促进中职数学教学质量提升[J].考试与评价，2017（10）：39.

[4]戴晨燕.妙用数形结合思想优化中职数学解题思维探讨[J].成才之路，2016（25）：56.