高中数学中数形结合方法的应用探讨
2024-01-07朱天云
朱天云
【摘要】数形结合是数学学习中一种应用广泛、效果显著的数学思想,能够促进学生对相关知识的深入理解,可以显著提高学生的数学兴趣,促使其能够主动进行相关知识的探究.在新高考背景下,数形结合思想在高中数学教学中的应用变得更加重要,这种数学思想强调的是学生对知识本质的理解,符合新时代课程改革理念.为了使数形结合方法能够得到良好的应用,文章从数形结合方法的内涵、应用意义、应用原则、应用现状以及应用策略上展开具体论述,以供参考.
【关键词】高中数学;数形结合;应用探讨
引 言
随着新课改的不断深入,传统的高中数学教学模式已经不能满足学生的思维发展需要,教师必须采取有效的措施进行教学模式的创新,对只关注教材中理论知识灌输的教学模式进行优化,注重对学生进行思维的训练,确保学生能够掌握知识的本质,从而实现知识的迁移与运用.但是从目前教师应用数形结合方法进行教学的现状来看,还存在教学内容陈旧、课堂互动少以及课后训练不足等问题,影响了数形结合方法作用的发挥.因此,相关教师需要深入反思,优化教学,提升学生的学习效率.
一、数形结合方法概述
数形结合指的是通过分析问题中条件与结论的关联,实现对代数意义的探究,同时展示出问题的几何性质.在数学中,数量的描述具有精确、严谨的特点,而几何图形具有形象、直观的特点,数形结合就是将二者进行融合,从而降低解题的难度,让数学学习变得更加轻松.从高中数学的角度上进行分析,数形结合在高中阶段具有重要地位.高中数学包含了大量的知识,并且具有一定难度,因此对学生的思维、能力等有着更高的要求,这就需要学生能够掌握一定的数学思想,并且能够进行有效的运用,以此来提高学习效果.因此,教师在进行高中数学教学时,应该注重对数学结合方法的有效利用,帮助学生牢固掌握相关数学知识.
二、高中数学教学应用数形结合方法的意义
(一)有利于提升课堂教学效果
数形结合方法的应用,可以显著降低解题难度,提高教学效果.学生在解决相关数学问题时,若是问题中仅仅提供了图形或者数据,那么就需要学生结合自己的数学认知,进行题目的转化,形成数据或者图形,这是一种高效的解题思想.也就是说,教师应该注重对学生数形结合思想的培养,让学生能够在看到数学语言时,大脑中形成对应的图形;在看到题目中的图形信息时,能够联想到图形对应的数量关系,以此来促进学生高效解题,提高他们做题的准确率.因此,教师在高中数学教学中,重视数形结合方法的教学,可以在一定程度上强化教学效果.
(二)有利于增强学生的学习兴趣
数形结合方法的核心是图形和数量的融合,不仅可以让问题变得更加直观,还可以在一定程度上提高解题的趣味性,有助于学生数学兴趣的提升,同时能够促进学生形象思维的生成.相比于小学和初中数学,高中数学在难度上显著提高,数学知识具有较强的抽象性、广泛性以及逻辑性.数学知识深度和广度的提高,让很多学生难以适应,不能理解相关知识的本质.久而久之,学生就会抵触数学学习,渐渐地对数学失去兴趣.而教师通过在教学中教授学生数形结合的方法,可以改善这种情况,能够实现对抽象知识的转化,让问题变得更加具象,促进学生深入理解相关知识的本质.
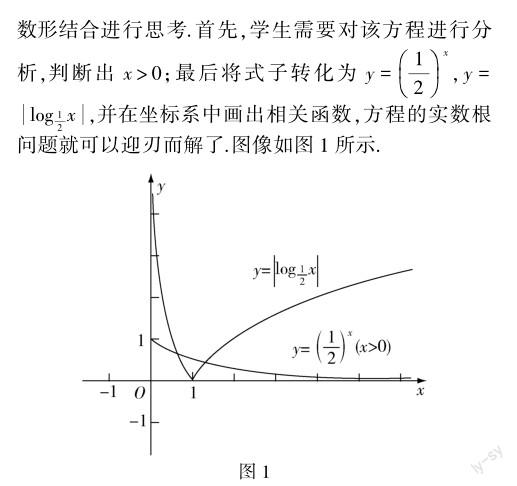
此时,学生可以根据图像去分析方程的实数根,最终求得此题的结果,图像有两个交点,所以方程的实数根有2个.这样大大降低了解题的难度,并且能够显著提升学生探究的兴趣.
(三)有利于学生思维的发展
数形结合是由“数”和“形”组成的,二者是对立统一关系.在数学学习中,“数”和“形”不应该独立存在,只有有机结合,才可以有效转化.这一过程中,学生的思维会得到训练,变得更加灵活,进而增强自身的学习能力.
例如,教师在教学“抛物线”相关知识时,可以通过数形结合的方式引导学生进行思考,使他们的思维得到训练.
例2 在抛物线y2=4x上有一点B,使得点B到y=x+3的距离最短.
该命题可转化为求一条平行于y=x+3的直线,y=x+b与抛物线y2=4x相切,求出切点,此时点B到直线y=x+3的距离最短,然后将y=x+b与y2=4x联立,可以求出B(1,2),使得点B到直线y=x+3的距离最短.图像如图2所示.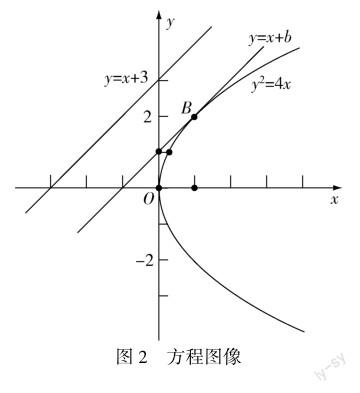
通过与图形结合的方式,知识变得更加直观,有助于学生思考,从而使学生正确解题.
三、高中数学教学应用数形结合方法的原则
教师想要让数形结合方法得到有效利用,那么在教学中应该遵循双向性原则.双向性指的是在数形结合中,“数”可以向“形”转化,同时“形”可以向“数”转化.在教学的过程中,教师应该结合问题实际,进行数形的转化.从图形上看,空间图形能够让数的特征清晰展现.而从代数上看,其主要特征是严谨精确,可以引导学生分析问题中的数量关系,还可以突破空间图形的直观约束,通过数更加深入地研究图形.也就是说,学生在利用数形结合进行解题时,不应该局限在数化形或者形化数上,应该考虑到双向性,将二者有机结合,才能够实现高效利用.
四、高中数学教学应用数形结合方法的策略
(一)利用数形结合方法优化教学内容
在教育改革不断深化的背景下,素质教育变得越来越重要.以往“一言堂”的灌输式教学已经是过去式了.在新时代的高中数学教学中,教师应该注重对学生思维的引导,促使学生能够主动进行知识的探究、思考知识的内涵和性质等.只有这样,才能提升学生的数学热情,让他们对抽象的数学形成长久的兴趣.数形结合可以有效训练学生思维,促进其主动学习.因此,教师在进行教学时,可以结合教材内容,进行数形结合方法的教学,从而实现内容的优化,同时通过这种方式帮助学生深度理解教材中的知识,让學生能够轻松地学习数学,为更高阶的知识学习打下基础.
教师应该从学生升入高中就开始就培养他们的数形结合思想.在教学的过程中,教师应该让学生对教材中“数”和“形”的内容进行区分,正确地对教材中数量和图形的内容进行分析,使学生可以利用数形结合的方法进行知识点的记忆以及题目的解决等等,让学生在数学学习的过程中潜移默化地形成数形结合思想.
例如,教师在进行“集合与常用的逻辑用语”这一章教学时,就应该深入分析教材,注重数形结合方法的渗透.如教师在讲解集合的概念时,就可以引入图形内容.集合的概念中涉及全集、交集以及并集等相关知识.为促使学生能够深入理解这些概念,教师可以带领学生进行相关图形的绘制,如图3所示.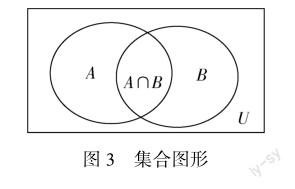

(二)利用数形结合方法提升学生的学习兴趣
兴趣是学生主动进行数学知识探究的动力.想要提高学生的学习效果,兴趣的培养十分关键.但是,从目前高中生对待数学的实际态度来看,很多学生对数学的兴趣并不高,特别是数学基础一般的学生,他们甚至对数学有厌烦心理.对于这类学生而言,他们不敢去分析具有较强抽象性的题目.比如,函数的最值问题,有些學生一看到最值问题,直接选择放弃.长期处于这样的状态下,学生的消极情绪就会逐渐累积,从而放弃学习数学,不再和教师进行互动,数学成绩也会出现大幅度下滑.针对这种情况,教师可以通过数形结合的方法,创设相关的数学情境,帮助学生理解数和形的关系,让他们通过回答教师的问题,产生学习数学的兴趣.
(三)利用数形结合方法强化课后训练
数形结合对数学学习具有重要作用,可以促使学生数学能力的不断提升.教师在利用数学结合方法进行教学时,应该将其应用到整个教学过程中,还应该将其融入课后的强化训练中,让学生能够充分地接触数形结合.课后训练是数学教学的重要组成,具有检验和巩固数学知识的作用.教师要重视让学生在课后训练中也能够进行数形结合方法的练习,使学生能够将数形结合思想内化于心,以此来不断提升学生的解题能力.下面以“不等式”题目教学为例.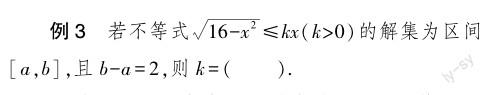
这道题通过正常求解十分复杂,通过图像法可以清晰地展示出题目答案.同时,学生在画图的过程中,思维可以得到有效训练.根据此题,可以得到如图4所示图像.
结 语
综上所述,数形结合是高中数学中重要的教学思想,可以促进教学效果的提升、学生兴趣的增强以及学生思维的发展.因此,教师应该注重数形结合方法的应用,在教学中运用等价性、双向性原则进行思想的渗透.同时,教师应该认识到自己在数形结合教学中的不足,有针对性地进行改进.
【参考文献】
[1]卢思聪.高中数学教学中数形结合方法的有效应用[J].高考,2021(20):24-25.
[2]陈建勤.高中数学教学中数形结合思想方法的应用[J].考试周刊,2018(18):69.
[3]牛菊霞.高中数学教学与解题中数形结合思想方法的应用分析[J].考试周刊,2021(12):75-76.
[4]田娟.高中数学教学中数形结合方法的有效应用[J].数学学习与研究,2021(2):25-26.
[5]王仁贵.浅析高中数学教学中数形结合方法的应用[J].学苑教育,2019(18):60-61.
[6]李晓明.高中数学教学与解题中数形结合思想方法的应用分析[J].中国新通信,2018(7):209.
