纸浆纤维种类和性质对其凝胶点浓度的响应关系研究

陈俊忠 王 超 左华伟 何广德 张文晖 赵 涛 张 雪张红杰，*

（1.永发（河南）模塑科技发展有限公司，河南滑县，314100；2.天津科技大学轻工科学与工程学院，天津，300457；3.中国制浆造纸研究院有限公司，北京，100102；4.制浆造纸国家工程实验室，北京，100102）

当前，“禁塑”“限塑”在全球范围内成为热潮[1]。我国和欧美发达国家相继出台了“禁塑”“限塑”的相关政策和法规，明确了未来一段时间内，塑料污染治理的具体时间表和路线图，这对于植物纤维基完全可降解材料来说是新的发展机遇，低定量的纸基软包装材料和纸浆模塑立体包装材料成为可以“替塑”“减塑”的绿色包装材料[2]。

上述绿色包装材料的机械性能和其他关键指标，均与植物纤维原材料的成形脱水过程和纤维网络的形成密切相关，本质上与纸浆纤维悬浮液的流变行为密不可分。纸浆纤维悬浮液的流变行为，在很大程度上取决于纸浆纤维悬浮液的固体质量分数（即浆浓）。纤维具有较高的长宽比时，可在全浆浓范围内发生明显的接触，这将显著地影响纸浆纤维悬浮液的流变行为[3]。纸浆纤维悬浮液基于浆浓通常可分成3大区域，即稀浆区、半稀区和浓浆区[4]。浆浓达到稀浆区与半稀区之间的边界时，纸浆纤维在液相中相互连接，并形成一种自支撑网络，这将严重影响纤维网络的成形脱水与再分布的可能性。这个浆浓连接阈值被定义为凝胶点浓度（Cg）[5]。因此，当浆浓低于Cg时，纤维网络不再稳定，易于发生单根纤维再分布现象，同时，不会对外表现出机械强度。

近年来，研究者试图预测或关联纸浆纤维的Cg。Kerekes 等 人[6]引 入 拥 挤 数（Crowding number 或Crowding factor）概念（即直径与纤维长度相等的球形体积中的纤维数量）来表征纤维间的接触情况，当拥挤数=60 时，纸浆纤维悬浮液中每根纤维将有3 个接触点，这将导致纤维在发生弹性弯曲时，在接触处产生法向力，由此产生的作用力将会赋予纤维网络机械强度。Martinez 等人[7]采用正电子放射断层造影术观察针叶木和阔叶木纤维的沉降情况，发现当初始拥挤数<16 时，纤维发生受阻沉降；而当初始拥挤数>16 时，纤维开始发生絮凝；基于此研究结果，初始拥挤数≈16 可以定义为纤维流动的亚区边界（即稀浆区与半稀区边界）。由此认为，Cg与纤维粗度（ω）和纤维质均长度（L）有关。Zhang 等人[8]在Martinez 等人理论（拥挤数理论）基础上推断出了纤维素纳米纤丝（CNF）的Cg与长宽比（A）的关系，并结合扫描电子显微镜和沉降实验结果，证实纤维的A越大，其Cg越低。Varanasi 等人[9]采用拥挤数理论和有效介质理论分别分析Cg与A的关系，发现2 种理论显示出合理的一致性结果，即Cg∝A-2。Li 等人[10]考察了漂白化学浆纤维悬浮液Cg的关联因素，发现凝胶点拥挤数（基于Cg计算得到的拥挤数）总体上与加拿大标准游离度（CSF）呈线性正相关关系。

Cg除了与纤维性质（L、ω、A等）密切相关外，还与体系pH 值、Ca2+浓度和絮凝剂浓度等因素有关。Sanchez-Salvador 等人[11]发现，pH 值的降低或CaCl2添加量的增加，会促进高度原纤化纳米纤维素（HFNC）絮凝，导致Cg降低，即连接所有纤维所需的HF-NC 数量减少。Li 等人[12]向微纤化纤维素（MFC）中加入2 mg/g 聚乙烯亚胺（PEI）或阳离子聚丙烯酰胺（CPAM），可以把Cg降低为原来的50%。Raj 等人[13]发现，CPAM 吸附并覆盖1/2 纤维表面时，基于架桥作用，可以增大MFC接触，导致Cg显著降低。

综上，研究人员已对Cg有了一定的认识，但主要集中在木浆、MFC 和CNF 等材料上，对于非木浆或相对较小A的纤维的Cg仍缺乏认识。本研究将考察木浆、竹浆和蔗渣浆的Cg，通过传统打浆和重刀切断打浆后再筛分的处理手段，得到不同性质的纤维，考察影响纤维Cg的因素。

1 实 验

1.1 实验原料

实验用漂白针叶木浆（以松木为主）为加拿大进口商品浆；漂白竹浆和漂白蔗渣浆为商品浆，分别购自贵州赤天化集团有限公司和广西湘桂华糖制糖集团来宾纸业有限责任公司。漂白针叶木浆、漂白竹浆和漂白蔗渣浆在下文分别简称“木浆”“竹浆”和“蔗渣浆”。

1.2 实验方法

1.2.1 传统打浆

采用标准Valley 打浆机（日本KRK 仪器制造公司）进行打浆，其中木浆和竹浆收集3 个打浆水平（未打浆、CSF 500 mL 和CSF 400 mL）的浆样，蔗渣浆收集2个打浆水平（未打浆和CSF 400 mL）的浆样。

1.2.2 筛分浆样

首先采用Valley 打浆机（济南初创机电设备有限公司）对木浆和竹浆进行重刀切断打浆，然后采用鲍尔筛分仪（美国TMI公司）分别对重刀切断打浆后的木浆、竹浆及未打浆的蔗渣浆进行筛分，筛分目数依次为30、50、100 和200 目，各筛网截留的浆样分别记为R30、R50、R100和R200，未筛分浆样记为R0。

1.2.3 沉降实验

向量筒内加入设定浓度的纸浆纤维，用玻璃棒搅拌均匀后静置8 h，记录沉降前液面高度H0与沉降后纤维层高度Hs。

1.3 表征方法

采用纤维质量分析仪（瑞典L&W 公司）分析纤维性质（包括纤维质均长度L、质均宽度W和粗度ω）。采用加拿大标准游离度测试仪（美国PTI 公司，ME-13）参照GB/T 12660—2008 中的方法进行测量。采用GB/T 29286—2012 中的方法测量纤维保水值（WRV）。

2 结果与讨论

2.1 纸浆纤维性质

表1显示了3种纸浆纤维不同打浆处理后的纤维性质比较。从表1可以看出，未打浆的木浆纤维最长（L=1.935 mm），其次是未打浆的竹浆（L=1.507 mm）和未打浆的蔗渣浆（L=0.697 mm）。经过传统打浆后，纤维质均长度、CSF和粗度均有所下降，保水值有所上升。纤维经过重刀切断打浆后再筛分，得到了4种不同级分的纤维R30、R50、R100 和R200，L、CSF 和ω依次降低，WRV依次增大。此外，无论是采用传统打浆还是重刀切断打浆后筛分，纤维质均宽度变化较小。

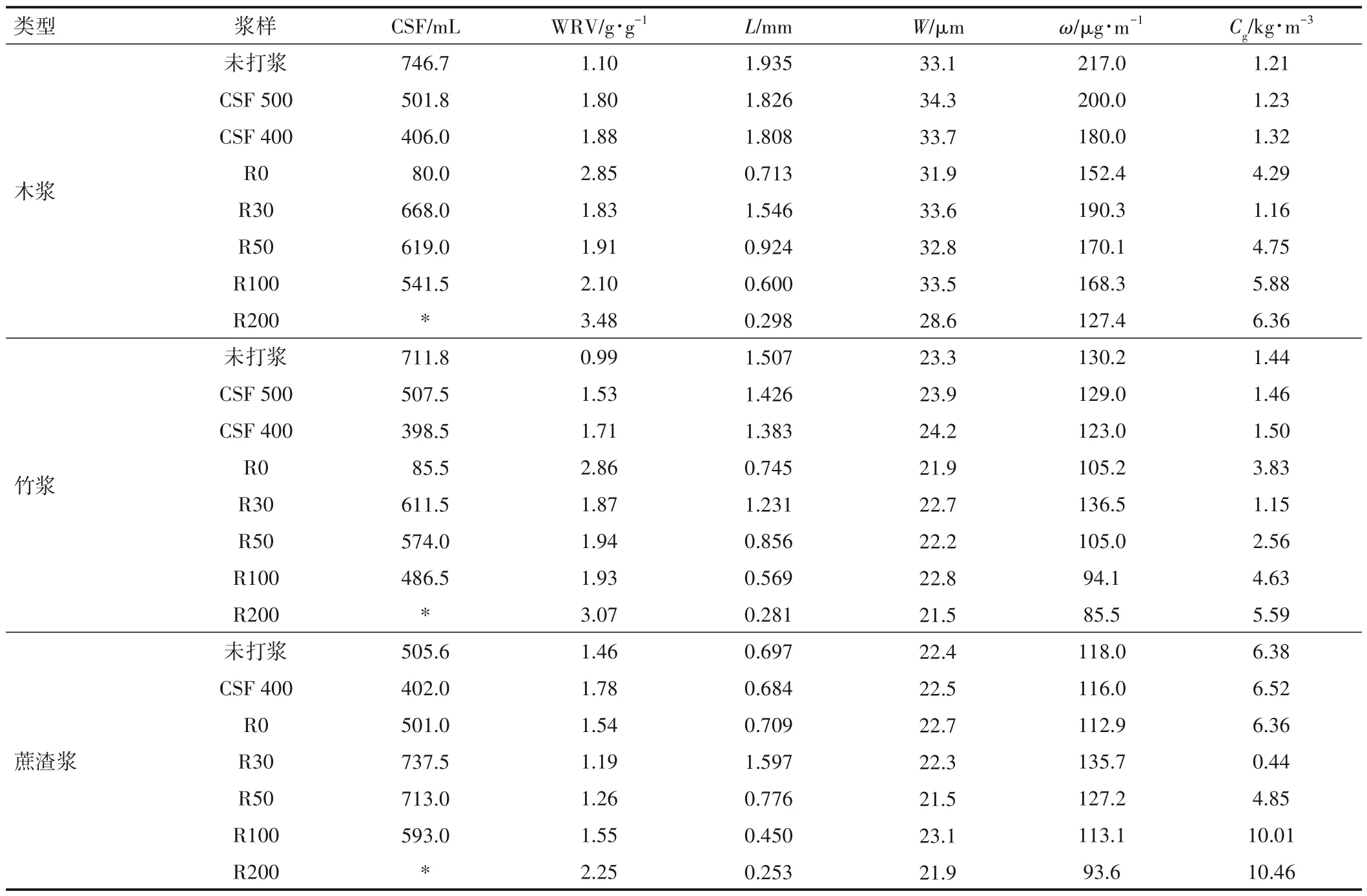
表1 3种纸浆纤维不同打浆处理后的纤维性质比较Table 1 Comparison of fiber properties of three types of fibers after different beating treatment

2.2 3种纤维不同打浆条件的Cg变化

图1 表示木浆、竹浆和蔗渣浆在传统打浆和重刀切断打浆并筛分后，纤维的沉降情况。从图1可以看出，在相同初始浆浓条件下，随着CSF 的降低（如图1(a)、图1(c)和图1(e)所示），3种纤维的沉降比（Hs/H0）均呈增大的趋势。如图1(b)、图1(d)和图1(f)所示，随着纤维级分从R30降低至R200，3种纤维的沉降比均呈降低趋势。进一步根据纤维的沉降情况，计算出凝胶点浓度（Cg，计算方式见式(1)和式(2)[11]），结果见表1。由表1可知，3种纤维的Cg均随CSF降低而增大，且增幅变化不大；采用重刀切断打浆并筛分后，当纤维级分从R30降低到R200，3种纤维的Cg均增大，并且Cg的变化趋势受纤维种类的影响明显。具体表现为纤维级分从R30降低到R200，木浆纤维的Cg从1.16 kg/m3增大到6.36 kg/m3，竹浆纤维的Cg从1.15 kg/m3增大到5.59 kg/m3，蔗渣浆纤维的Cg从0.44 kg/m3增大到10.46 kg/m3。经过传统打浆后，纤维会发生分丝帚化和切断现象。对比WRV 和L的变化，前者变化范围为20%～70%，后者变化小于8%，因此传统打浆主要以分丝帚化为主，纤维间接触点增大，形成纤维网络所需最少纤维数量将降低，这最终导致纤维沉降高度增大，Cg降低。当采用重刀切断打浆时，对比WRV的变化程度（159%～188%）和L的变化程度（50%～63%）可知，重刀切断打浆以纤维切断为主要因素，分丝帚化为次要因素。纤维变短后，纤维形成的堆积密度增大，导致纤维沉降高度降低。基于拥挤数理论和有效介质理论[7,9]可知，在纤维粗度或宽度变化不大时，纤维长度降低会提高Cg。

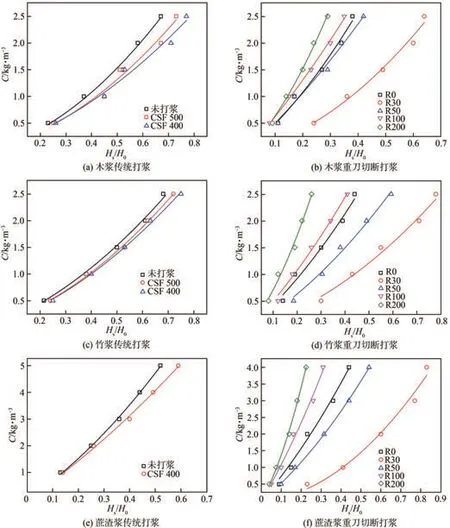
图1 3种纤维在不同打浆条件处理后纤维的沉降情况Fig.1 Sedimentation of three types of fibers under different beating conditions

式中，H0为沉降前液面高度，Hs为沉降后纤维层高度，C为初始纸浆悬浮液浓度，a、b为拟合系数。

2.3 不同纤维性质对其Cg的影响

2.3.1 CSF与Cg的关系

图2为CSF与Cg的关系。从图2可以看出，尽管总体上Cg随CSF的增大呈下降趋势，但波动的幅度很大，且受纤维种类影响明显，这说明CSF与Cg的相关性较差。这与Li等人[10]的结论有所不同，即CSF与Cg存在一定正线性相关。其主要原因在于：①计算凝胶点浓度的方式不同，本研究采用最常用的Martinez 方法[7,9,14]，并基于纤维沉降比计算Cg，Li 等人采用Usher 方法[15]，基于纤维底层压力计算Cg；②研究样本大小的差异，本研究采用传统打浆和重刀切断打浆并筛分处理3种不同纸浆纤维样本，Li等人仅考察漂白硫酸盐木浆经过PFI磨浆后的纤维样本，前者Cg变化范围很大（0.4～10.64 kg/m3），后者Cg变化范围很小（2.02～2.41 kg/m3）。

图2 CSF与Cg的关系Fig.2 Relationship of CSF and Cg

2.3.2 WRV与Cg的关系

图3为WRV与Cg的关系。从图3可以看出，对于同一种纸浆纤维，WRV 与Cg存在一定的正相关关系，即随着WRV的增大，Cg总体上也随之增大。同样可以看出，纤维种类对Cg影响很大，如在相同WRV 条件下，竹浆和木浆的Cg较低，而蔗渣浆的Cg较高。考虑到WRV不仅与纤维的分丝帚化程度有关，还与纤维质均长度（L）等性质有关，有必要进一步确认纤维的L或A与Cg的关系。

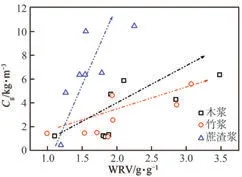
图3 WRV与Cg的关系Fig.3 Relationship of WRV and Cg

2.3.3L与Cg的关系

图4 为L与Cg的关系。从图4 可以看出，当L从0.2 mm 增大至1.2 mm 时，随L的增大，总体上Cg呈降低趋势，纤维种类对Cg有较大的影响；当L进一步增大至2.0 mm，Cg变化较小，且纤维种类对Cg的影响较小。基于纤维悬浮液的流变学理论[3,16]可知，纤维网络的形成与L、浆浓和ω有关。结合图4 可知，纤维越长，在给定空间内纤维间接触概率越高，越易形成纤维网络，因此纤维越长，达到连续纤维网络所需要纤维数量越少，即Cg越低。

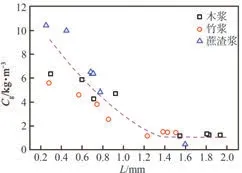
图4 L与Cg的关系Fig.4 Relationship of L and Cg

2.4 基于拥挤数理论和有效介质理论分析不同纤维的Cg

Martinez 等人[7]发现针叶木浆纤维和阔叶木浆纤维的Cg与ω/L2呈正比。Varanasi 等人[9]基于拥挤数理论分析发现Cg与A2呈反比，基于有效介质理论分析发现Cg与A1.724呈反比。图5表示了Cg与ω/L2和A关系。从图5 可以看出，Cg随ω/L2、A-2或A-1.724变化趋势基本相同，可分成2 大区域，在低值区域存在线性关系，且基本不受纤维种类的影响；在高值区域变化很小，受纤维种类的影响。基于拥挤数理论分析，凝胶拥挤数Ng=0.5CgL2/ω=12.0，与Martinez等人[7]的结论Ng=16±4 相似。在高值区域的非线性关系无法直接用拥挤数理论或有效介质理论来解释，主要原因可能是这个区域内纤维的A较小（<20），纤维比表面积更高，纤维之间的接触受表面电荷影响更大。因此，纤维网络不仅受纤维的物理性质（如L、W和ω）影响，还受纤维表面电荷影响[12-13]。

图5 Cg与ω/L2和A的关系Fig.5 Relationship of Cg and ω/L2 or A

3 结 论

本研究考察了漂白针叶木浆、漂白竹浆和漂白蔗渣浆3种纸浆纤维的沉降情况，研究了纤维性质对纤维凝胶点浓度的影响。

3.1 加拿大标准游离度（CSF）与凝胶点浓度存在一定负相关关系。

3.2 随着纤维保水值增大，凝胶点浓度总体上随之增大，且变化趋势受纤维种类影响明显。

3.3 随着纤维质均长度增大，凝胶点浓度随之降低，当纤维质均长度增大到1.2 mm 时，凝胶点浓度基本不变。

3.4 凝胶点浓度随粗度/长度2（ω/L2）、长宽比（A-2）或A-1.724变化趋势基本相同，可分成2大区域，在低值区域存在线性关系，且基本不受纤维种类的影响。高值区域无法直接应用拥挤数理论或有效介质理论解释，需要考虑表面电荷等非物理性纤维性质参数。