“数形结合”为主线的整体教学设计
——以“反比例函数与矩形”的探究课设计为例
2024-01-06广东省深圳实验学校初中部邮编518000
广东省深圳实验学校初中部 秦 哲 (邮编:518000)
1 前言
《义务教育数学课程标准(2022年版)》强调改变过于注重以课时为单位的教学设计,推进单元整体教学设计,体现数学知识之间的内在逻辑关系,以及学习内容与核心素养表现的关联[1].推进“整体教学”需加强数学知识之间的联系,以“更高”“更宽”的视角进行数学课程设计,让学生在问题解决中,体会数学的学科特征,感受并理解数学的内在逻辑,不断提升数学核心素养.
《义务教育数学课程标准(2022年版)解读》强调主题单元是培养学生核心素养的重要形式,以数学思想为主线是确定主题单元的重要组织方式[2].多年来,反比例函数一直是中考的热点和难点,它常常与平面几何的知识相结合,从而增加试题的复杂性和难度,对学生的综合能力提出挑战. 本文对2019年抚顺中考数学题进行变式拓展,通过改变问题条件,以“数形结合”的数学思想为主线来架构单元内容结构,围绕“矩形的两个顶点能否同时在反比例函数的图象上”这一探究主题对教学内容进行重组和整合,为“整体教学”提供范例和思考,供大家讨论.
2 教学设计

问题1如图1,求点C的坐标.(2019年抚顺中考数学题)
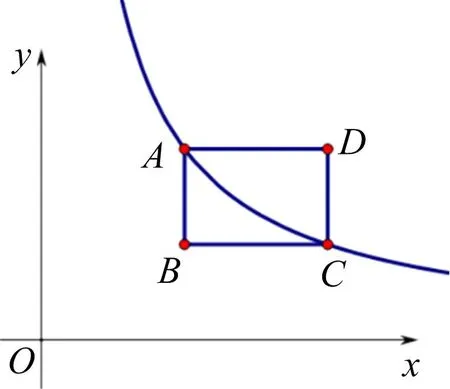
图1
C(6,2),解析略.
问题2如图2,连接BD与反比例函数相交于点K,求点K的坐标.
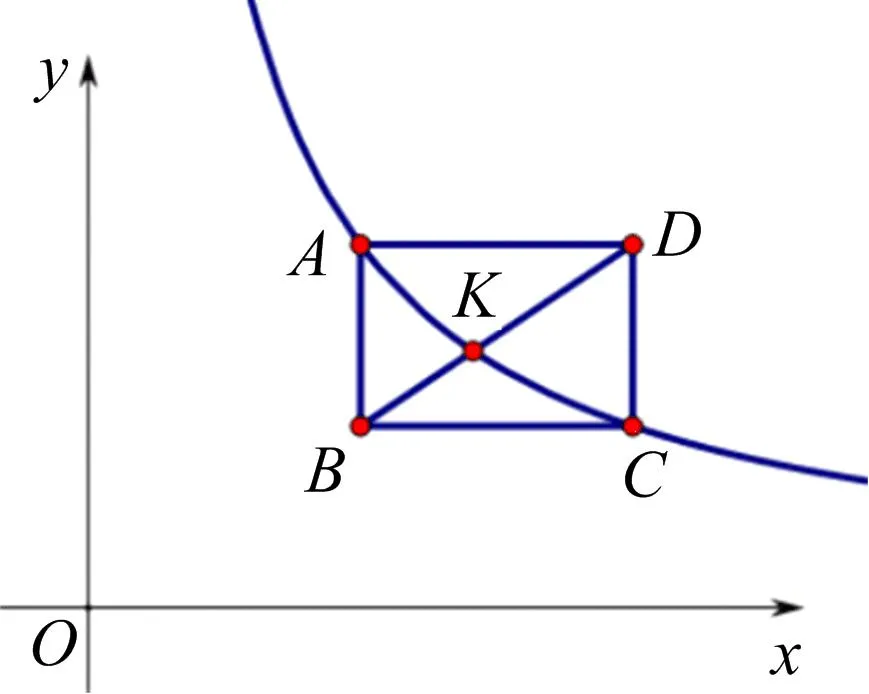
图2
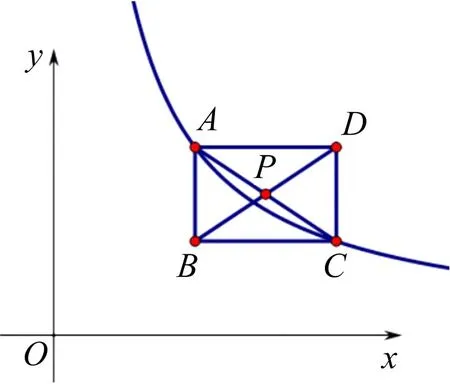
图3
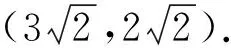

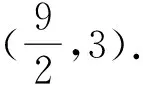
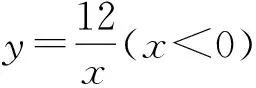


图4

评注通过改变问题结构,拓展了3个问题,旨在帮助学生巩固解决函数问题的方法和技巧.问题2巩固求交点的重要方法:联立方程;问题3引导学生通过不同方向对点P进行平移:水平方向、垂直方向、沿射线方向等等,拓展学生问题解决的思路.问题4引导学生利用“数”与“形”两种视角解决问题,发展“数形结合”思想:方法1利用反比例函数解析式建方程;方法2关注“反比例函数图象的中心对称性”.
3 问题拓展

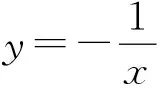
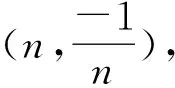
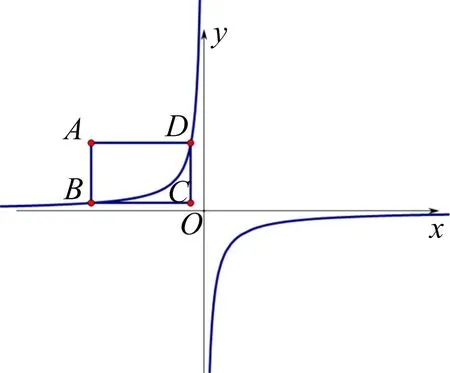
图5
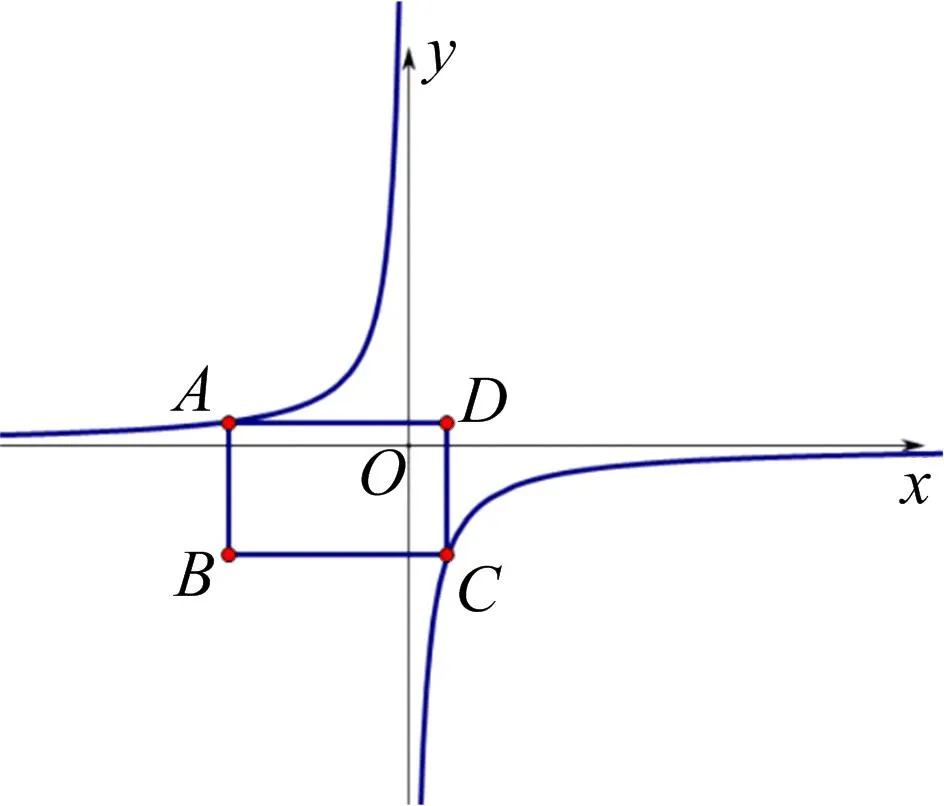
图6
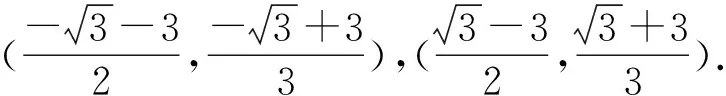
评注法国数学家笛卡尔说过:“我所解决的每一个问题,将成为一个模式,以用于解其他问题.”数学的问题千变万化,看似毫不相关,表面上存在差异的问题,本质的结构是相同的,都能使用相同的方法和思路进行解决.问题1是对例题1的发展和延伸,学生需更加全面地分析问题,并将问题分为两种情况,再利用例题1中问题4的方法进行解决,学生经历问题解决不断巩固解题技巧和方法,加深对矩形与反比例函数的性质的理解.
问题2结论:“当k<0时,无论k取何值,若矩形ABCD有两个顶点在反比例函数的图象上,则符合条件的顶点A一定有4种”,请判断此结论是否正确,并说明理由.
根据前面的学习经验,将问题进行分类:情况1. 顶点B和顶点D在反比例函数图象上;情况2. 顶点A和顶点C在反比例函数的图象上.如图7,可让学生用GeoGebra来直观感受这个结论是否正确,改变反比例函数的k值,拖动矩形ABCD去验证矩形ABCD的两个顶点是否同时在反比例函数的图象上.

图7
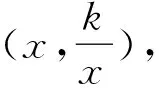

评注问题2由问题1的“确定性问题”拓展为“存在性问题”,解决方法和思想一脉相承,通过设点坐标,利用线段的数量和位置关系构建方程.学生在GeoGebra软件中改变k的大小,拖动矩形ABCD的位置,通过直观地理解和分析得到一个初步的结论,观察和猜想得到的结论不一定是正确,需通过严谨的数学证明,证明的关键是将几何问题利用“数形结合”的思想“转化”为代数问题进行解决,感受“数形结合”的魅力,深化对“方程”和“转化”数学思想的理解,提升学生综合运用反比例函数的概念、解析式、图象等性质解决问题的能力.
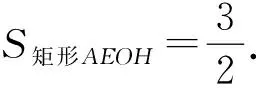
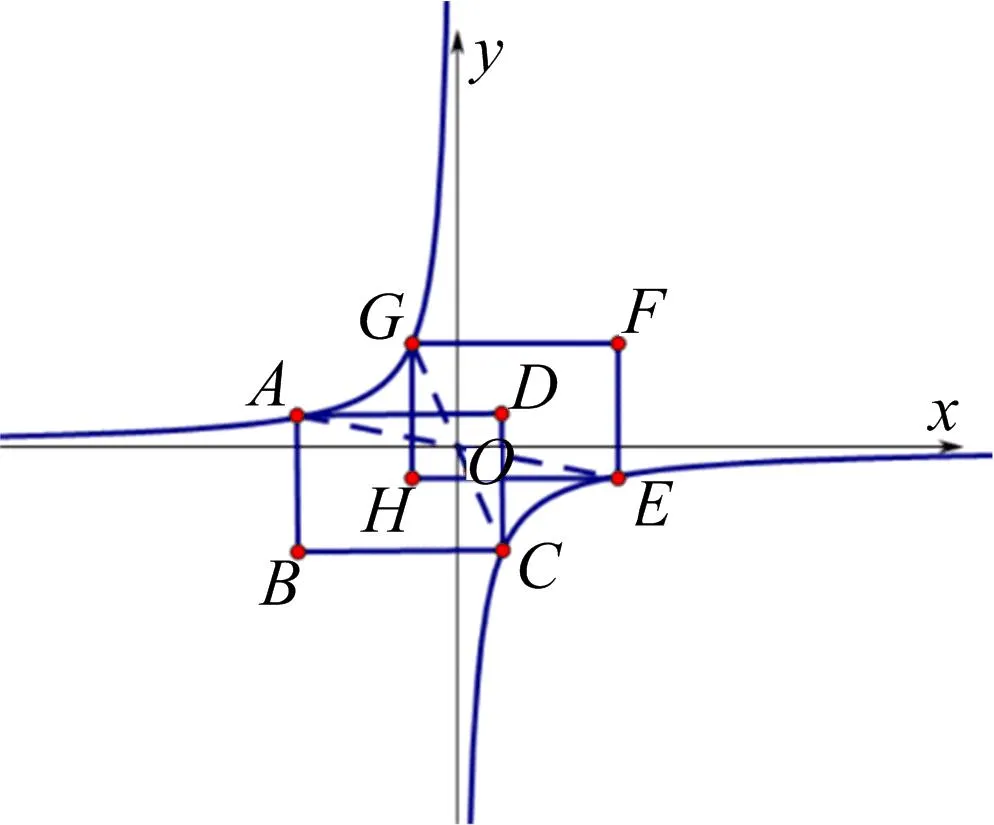
图8

图9

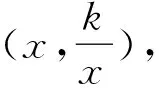

图10
评注问题3关注“变化”中的“不变性”,虽然反比例函数的解析式和矩形ABCD的位置“变化”,但直线AC始终经过原点,学生继续使用GeoGebra软件探究变化,不断提升动态的数学思维.在问题解决中,有学生会利用参数k表示点A和点C的坐标,进而求出AC的解析式,得到直线AC的截距为零,进而证明直线AC经过原点,此方法正确,但方法复杂,教师在教学中适当肯定与提醒.
4 感悟与思考
数形结合主要指“数”与“形”之间的一种一一对应关系,其实质就是实现抽象的数学语言、复杂的数学关系与直观的几何图形、明了的位置关系之间的相互转化,将抽象思维与形象思维相结合[3].前文阐述了以“数形结合”思想为主线的单元整体教学设计,通过研究与矩形ABCD的两个顶点在反比例函数图象上有关的存在性问题,不断发挥直观对抽象的支撑作用,用代数方法分析几何图形,促进问题的逻辑化理解;利用几何方法分析代数,洞察数学问题的本质,“数”与“形”优势互补,相辅相成.
《义务教育数学课程标准(2022年版)》强调应根据学生已有的知识经验、认知水平、学习要求,结合具体内容特点系统规划单元教学目标,整体把握结构化的课程内容,选择能促进学生思考的教学方式,在教学中整体设计、分布实施[1].例题1旨在巩固反比例函数的基础知识,理解并强化解题的基本方法和技巧,如:利用矩形的性质和反比例函数的解析式构建方程解决问题等等;例题2中的矩形ABCD“动”起来了,由例题1的“静态问题”变为与“存在性”有关的“动态问题”, 在问题1中,学生联系“旧问题”解决“新问题”,问题3又引入反比例函数和一次函数的图象变化,进一步加强数学知识的联系. 问题设置由易到难,由“单一”到“综合”,帮助学生理解知识的本质,从解题技能层面延伸至数学思想和方法的内化与巩固,促进知识相互迁移与拓展,培养综合运用的能力.
在平时的教学中,有许多“数形结合”有关的知识内容:一次函数图象上点的坐标与二元一次方程的解,一次函数与二次函数的交点坐标与一元二次方程的解等等,若只就单一的知识点或习题进行讲解则无法有效渗透“数形结合”的数学思想,应充分考虑课程内容的结构和学生的学习特点与认知水平,充分挖掘知识之间的内在联系,以“整体教学”统领课程设计. 而“整体教学”并不是把各种数学知识松散地拼凑在一起,应以某个数学思想为主线、某个数学知识为主题,如:本文以反比例函数的数学知识为主要内容,充分整合反比例函数、矩形、一次函数等知识,以问题串的形式形成探究活动,沿着主题知识相关的内容进行探究和拓展,将探究活动中总结的技巧和思想方法串联起来,帮助学生厘清知识之间的逻辑关系和脉络体系,形成系统化的知识体系. 本文中的问题可继续拓展:例题2的问题3中,若矩形ABCD的顶点A和C在反比例函数的图象上,那么直线BD一定经过原点吗?等等.教师在教学中关注问题的“生长”,引发学生不断思考,延伸课程内容,产生新的问题,帮助学生拓展数学视野,让学生在不断的问题解决中增加兴趣,享受成就感.
