黏性土边坡临界滑动面确定的新方法
2024-01-06张爱卿李金云
张爱卿, 李金云, 单 炜, 郭 颖
(1. 北华航天工业学院 建筑工程学院, 河北 廊坊 065000; 2. 东北林业大学 寒区科学与工程研究院, 黑龙江 哈尔滨 150040)
边坡临界滑动面的确定是研究边坡稳定性的关键问题之一[1-4].国内外学者对于边坡临界滑动面的确定做了大量卓有成效的研究.Cheng等[5]和Sultan等[6]分别从理论上研的确定方法.李宁等[7]提出利用摩擦-接触型界面单元模拟滑动面.介玉新等[8]提出了采用最大加速度评价边坡安全性的方法.杨建成[9]提出一种新的局部强度折减法,其分析结果与工程实际情况吻合较好.张玉成等[10]利用有限元法对边坡的变形场和应力场进行分析,并以此确定滑动面.蒋泽锋[11]充分利用大数据处理技术建立了边坡临界滑动场计算系统.综上所述,国内外学者多是在有限元理论的框架下,以安全系数为评价指标来确定边坡临界滑动面,其并不适合公路检测人员现场操作应用.
近年来简易贯入法在工程检测中得到了大量的应用.潘芷加等[12]利用简易贯入法分析了灾害场地土层土壤的软弱特性.郭颖[13]利用简易贯入法探测出冻土地区土体融化深度.李金云等[14]将简易贯入法作为确定低液限黏土路基压实度的新方法.因此,引入简易贯入法作为确定黏性土边坡临界滑动面的新方法,构建简易贯入次数与承载力的关系式,选取某公路黏性土路堑边坡,实测简易贯入次数,计算得出边坡承载力值,并绘制边坡承载力突变点曲线图,依此确定边坡临界滑动面,并与有限元法和理论方法进行比对,为快速准确地确定黏性土边坡临界滑动面提供了新的方法.
1 简易贯入次数与承载力的关系
1.1 简易贯入试验
简易贯入试验属于动力触探的一种,由于该试验设备简单、操作方便和土层的适用范围广,被广泛应用于判断土体的物理力学性质[15-16],其组成如图1所示.简易贯入试验是将穿心锤放置一定高度后自由落下,使势能转化为贯入土体的动能.

图1 简易贯入试验仪组成Fig.1 Composition of simple penetration tester
研究表明[14-15]:当触探杆贯入土层深度为10 cm时,记录此时的锤击数,以此判定土的力学特性.
式中:Δh为触探杆贯入土层的深度,m;hn为第n次锤击时卷尺的读数,cm;hn-1为第n-1次锤击时卷尺的读数,cm;N为锤击次数,次;Nd为所求的实测击数,次.
1.2 简易贯入次数与承载力的关系式
对于地基承载力可以通过标准贯入次数确定,当土体为黏性土或粉土时,按照《建筑地基基础设计规范》[3]要求,选取黏性土承载力标准值与标准贯入击数的关系作为标准贯入次数与地基承载力的关系,关系式如下:
fk=19N-74
(3)
式中:N为标准贯入次数,次;fk为地基承载力,kPa.
已知简易贯入试验与标准贯入试验的贯入次数存在着2倍的关系[16-17].借鉴标准贯入次数与地基承载力的研究结果,在公式(3)的基础上建立简易贯入次数与承载力的关系式.
fkj=9.5Nj-74
(4)
式中:Nj为简易贯入次数,次;fkj为承载力,kPa.
2 简易贯入法确定黏性土边坡临界滑动面
以边坡失稳现象多发、具有代表性的黑龙江省同三高速公路K560+580路段的左侧黏性土边坡为研究对象,浅层土体(3 m以内)为黄色粉质黏土,土层及其物理力学参数见表1所列[13].先确定检测点,后利用简易贯入法开展现场试验,分析检测数据,确定黏性土边坡临界滑动面.
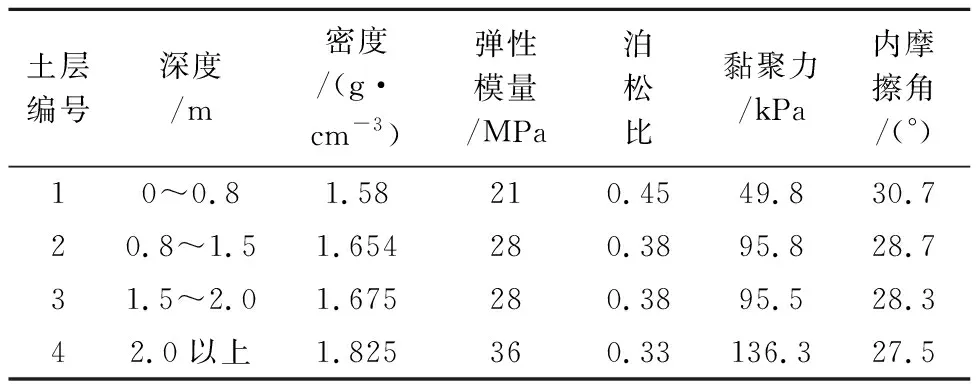
表1 边坡黏性土物理力学参数
2.1 简易贯入法测点布设及现场试验
K560+580路段左侧黏性土边坡高度为6 m,坡脚为31°.现场布设检测点示意图如图2所示.由图2可知,①号和②号、⑧号与⑨号两组检测点间距为1 m,其余检测点间距相同,均为2 m.试验步骤严格按照文献[14]的要求进行,同一检测点位置做三次简易贯入试验,三次试验结果相差在5%以内的可以取平均值,并记为简易贯入试验的贯入次数.

图2 黏性土边坡检测点示意图(mm)
2.2 试验结果及分析
将试验数据代入公式(4)中计算边坡承载力值,并绘制边坡承载力与深度的关系曲线,如图3所示.
由图3可知,边坡承载力随着贯入深度增加呈锯齿状不断变化,其中在检测点1号至6号的曲线中,均存在一个折点处的边坡承载力值近似等于0,将边坡承载力近似等于0的点定义为边坡承载力突变点.检测点7号至9号未出现这样的突变点,表明边坡临界滑动面应通过检测点1号至6号位置的边坡断面,而未通过检测点7号至9号位置的边坡断面.
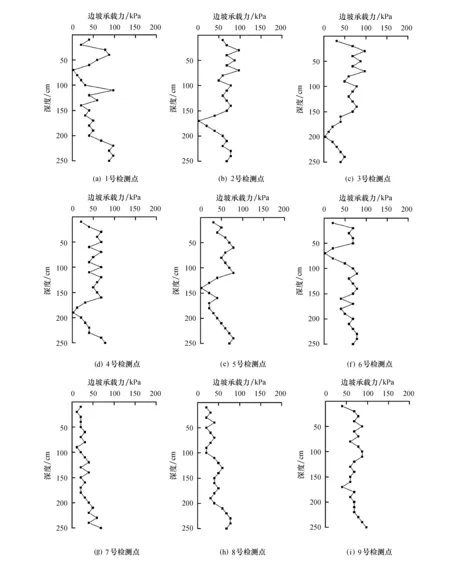
图3 9个检测点的简易贯入试验结果
同时注意到检测点7号和8号相对于其他7个检测点的边坡承载力值偏低,表明这两个检测断面处的边坡土体稳定性差,有可能在滑坡条件成熟情况下伴随着边坡滑动体产生向下的滑动.
从图3曲线中搜索①号至⑥号中边坡承载力突变点所对应深度,在图2上进行标记,并连线,如图4中1号折线所示.
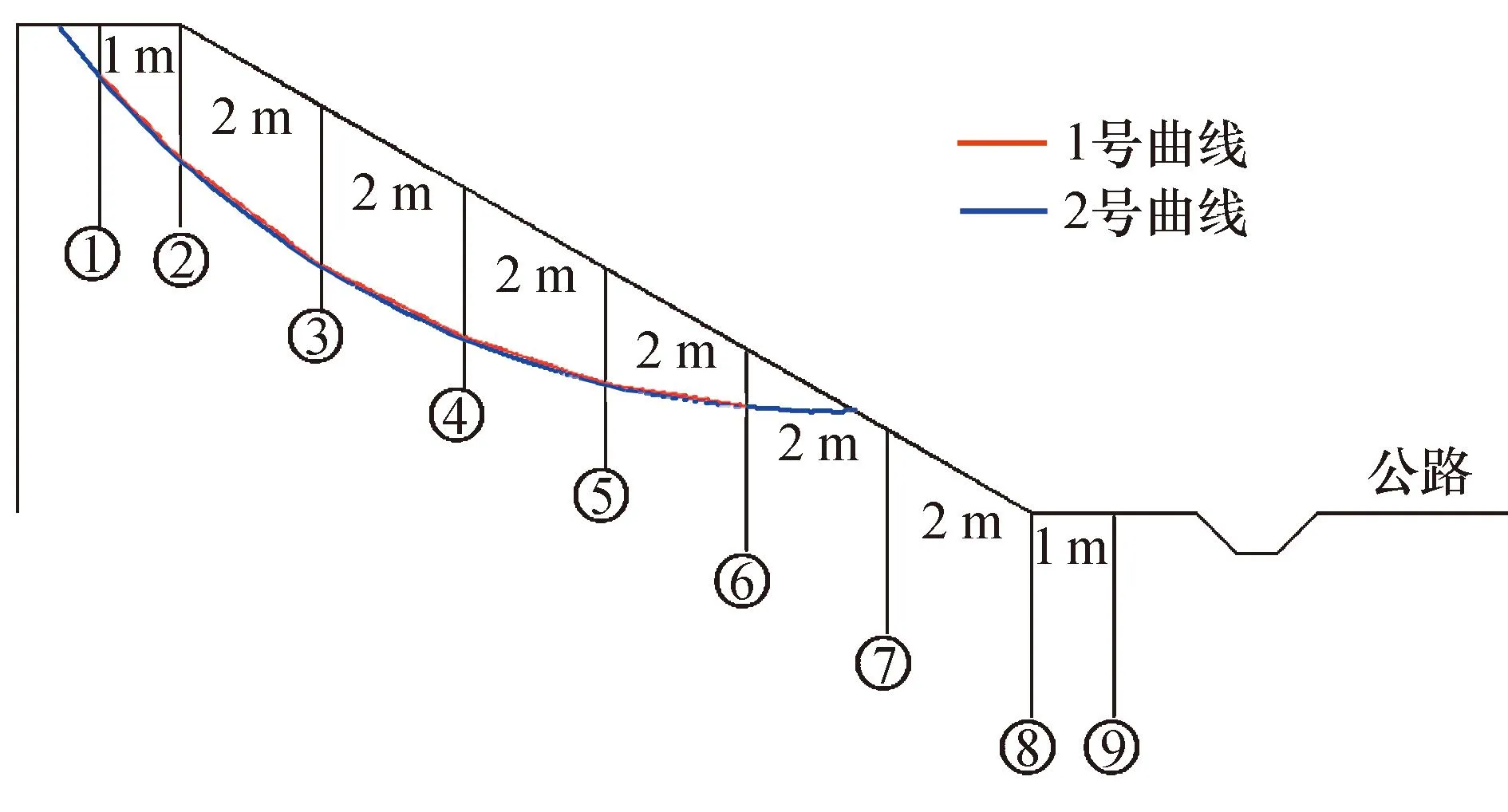
图4 边坡承载力突变点弧形曲线图(mm)Fig.4 Curve curve of abrupt transition point of slope bearing capacity (mm)
观察图4可知,边坡承载力突变点的连线线近似为弧型曲线,且该弧型曲线穿过检测点1号至6号,利用CAD软件将弧型曲线的两端与边坡边界相连,得到一条完整的弧形曲线,将最终得到的弧形曲线作为边坡临界滑动面,如图4中2号曲线所示.
综上可得,简易贯入试验在搜寻边坡临界滑动面过程中,若边坡承载力为0的点出现,意味着边坡存在滑坡的可能性,应采取措施对边坡进行加固处治.
下面将利用有限元法和理论方法验证试验方法的可行性和合理性.
3 简易贯入法与有限元法和理论方法的对比
3.1 简易贯入法与有限元法的对比
采用与工程实际相吻合的局部强度折减法来对工程实例进行数值计算[9-10].表达式如下:
(5)
式中:c′为折减后的黏聚力值,kPa;φ′为折减后的内摩擦角,(°);F为折减系数.
根据文献[9]中给出的计算步骤,按照图5所示的边坡几何示意图,利用ABAQUS有限元数值模拟软件进行计算,暂不考虑黏性土边坡在不同深度处土体物理力学性质的差异,其重度为17 kN/m3,弹性模量为28 MPa,泊松比为0.38,黏聚力为92.3 kPa,内摩擦角为26.92°.
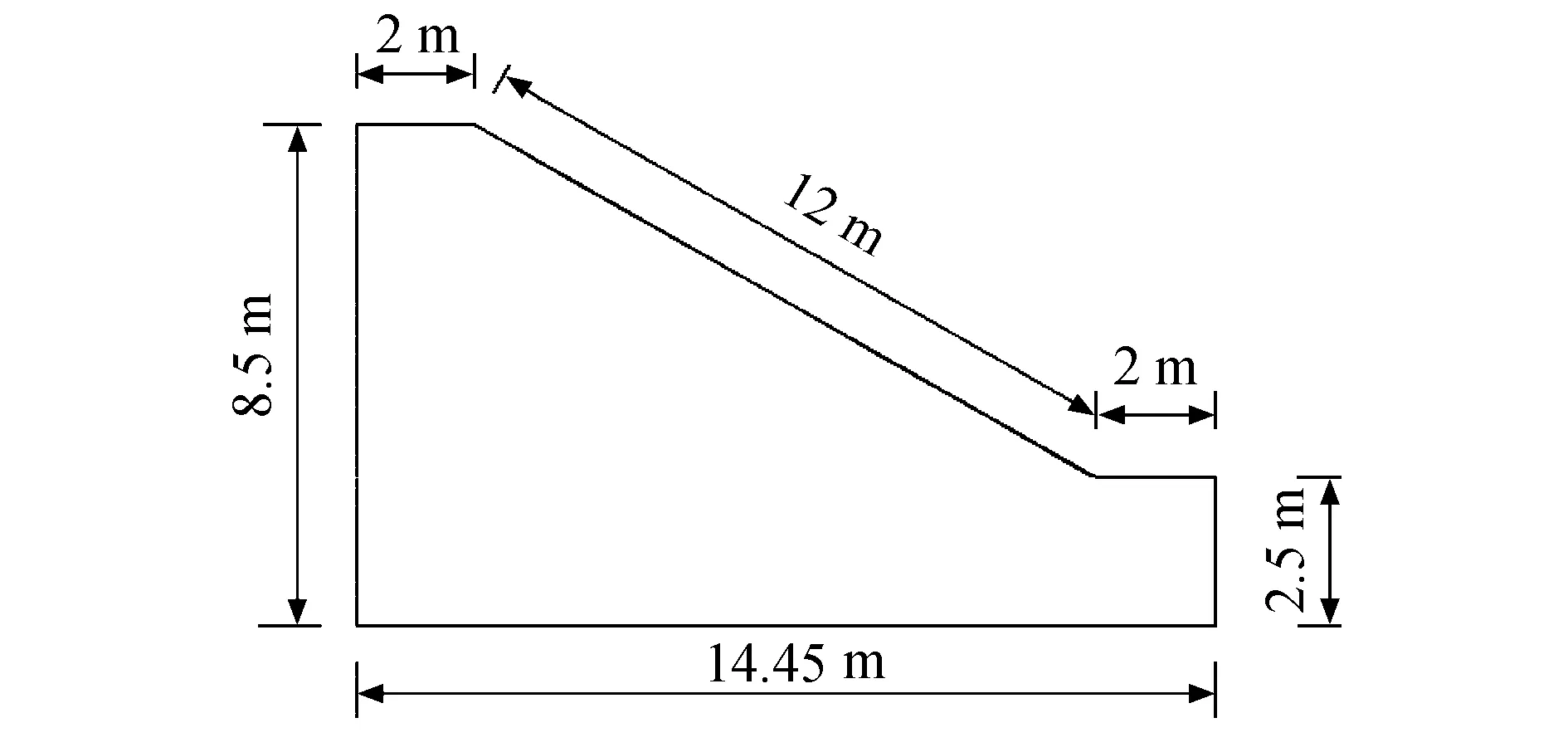
图5 边坡几何示意图Fig.5 Geometrical diagram of slope
经过数值计算得出该黏性土路堑边坡安全系数(折减系数)为1.25,边坡潜在滑动面的范围为图6中采用有限元法圈定的范围.
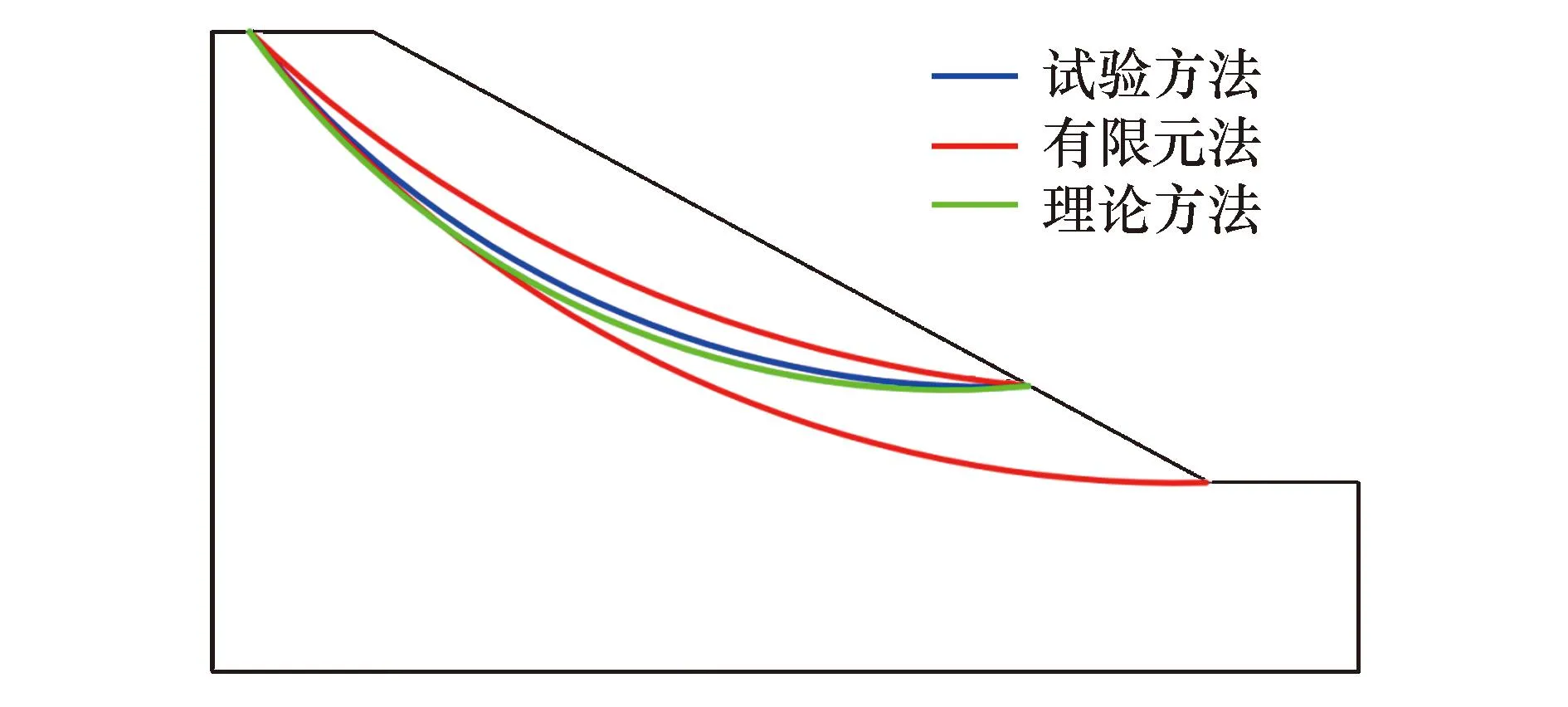
图6 试验方法与有限元法、理论方法计算结果对比Fig.6 Comparison of calculation results between the method presented in this paper and the finite element method and theoretical method
由图6可知,试验方法得出的边坡临界滑动面在采用局部强度折减法计算出的边坡潜在滑动面范围之内.简易贯入试验中7号和8号检测点低于其他检测点的边坡承载力值,原因是这两个检测点均处于边坡潜在滑动面范围之内所导致.研究表明试验方法得出的结果与有限元法得出的结果一致性好,验证了简易贯入法在确定黏性土边坡临界滑动面的可行性.
3.2 简易贯入法与理论方法的对比
临界滑动面被用来表征边坡失稳时最可能出现的滑动位置.采用滑动圆弧法对该模型进行理论计算,首先通过4.5H法确定滑动圆弧的圆心位置,再对其滑动圆弧进行分条,计算滑动面的总滑动力矩和滑动面的总抗滑力矩,最后计算出每一个滑动面的安全系数,其中安全系数为1.05的滑动面即为最危险滑动面,其计算结果见图6所示.
由图6可知,试验方法确定的边坡临界滑动面与理论计算出的边坡最危险滑动面基本一致,表明简易贯入法得出的结果可以应用于工程实际,验证了简易贯入法在确定黏性土边坡临界滑动面的合理性.
综上所述,简易贯入法相比有限元法,其结果更具真实性和代表性;相比标准贯入试验为代表的传统边坡临界滑动面确定方法,不仅检测点多,而且快捷准确.
工程实际中一般以坡高6 m作为黏性土边坡是否设置平台的依据,对于单级黏性土边坡(坡高小于等于6 m)可直接利用简易贯入法来确定边坡临界滑动面;对于多级黏性土边坡(或单级坡高超过6 m),可参考《标准贯入试验规程(YS/T 5213—2018)》中要求对杆长进行修正,因此,对于多级黏性土边坡建议采用简易贯入法和有限元强度折减法共同分析、综合确定边坡临界滑动面.
4 结论
1)在研究简易贯入试验原理的基础上,借鉴标准贯入次数与地基承载力研究成果,建立了简易贯入次数和边坡承载力之间的关系式.
2) 简易贯入试验表明,边坡承载力随着深度增加呈锯齿状不断变化,在贯入深度范围内发现了边坡承载力近似等于0的突变点,将突变点标记到边坡横剖面上并连线得到边坡临界滑动面.
3) 简易贯入试验方法与有限元法相比一致性好,与理论计算结果相比符合工程应用要求.验证了简易贯入法在确定黏性土边坡临界滑动面的可行性和合理性.
致谢:本文得到北华航天工业学院科研基金项目(BKY-2020-24)的资助,在此表示感谢.
