Deep Learning-Assisted OFDM Detection with Hardware Impairments

Amit Singh,Sanjeev Sharma,Kuntal Deka,Vimal Bhatia

Abstract—This paper introduces a deep learning (DL)algorithm for estimating doubly-selective fading channel and detecting signals in orthogonal frequency division multiplexing (OFDM) communication systems affected by hardware impairments (HIs).In practice,hardware imperfections are present at the transceivers,which are modeled as direct current (DC) offset,carrier frequency offset (CFO),and in-phase and quadrature-phase (IQ)imbalance at the transmitter and the receiver in OFDM system.In HIs,the explicit system model could not be mathematically derived,which limits the performance of conventional least square (LS) or minimum mean square error (MMSE) estimators.Thus,we consider time-frequency response of a channel as a 2D image,and unknown values of the channel response are derived using known values at the pilot locations with DL-based image super-resolution,and image restoration techniques.Further,a deep neural network (DNN) is designed to fit the mapping between the received signal and transmit symbols,where the number of outputs equals to the size of the modulation order.Results show that there are no significant effects of HIs on channel estimation and signal detection in the proposed DL-assisted algorithm.The proposed DL-assisted detection improves the OFDM performance as compared to the conventional LS/MMSE under severe HIs.

Keywords—OFDM,DL,HIs,channel estimation,signal detection

I.INTRODUCTION

Orthogonal frequency division multiplexing(OFDM)is a prominent modulation scheme used in 4G and 5G wireless systems.OFDM divides the high serial data rate channel into low data rate multiple channels,which reduces the equalization complexity significantly by doing detection in the frequency domain.OFDM supports multi-user access and shows better resistance to multi-path fading channels[1-3].OFDM is a multi-carrier modulation technique and it has wide-area applications in digital audio broadcasting (DAB),digital video broadcasting (DVB),local area networks (LAN),etc.It also has the ability to suppress inter-symbol interference (ISI)[4].In OFDM,each frequency subcarrier experiences an independent channel,which improves diversity of a wireless system.However,OFDM system’s performance depends on channel estimation and signal detection methods.Further,different hardware impairments (HIs) affect OFDM performance in practice[5-6].Therefore,robust channel estimation and signal detection methods are essential for OFDM system,particularly in the presence of different HIs.

Least square (LS) and minimum mean square error(MMSE) estimators and their modified methods are commonly used for channel estimation in the OFDM system.The LS method does not yield good results as compared to MMSE due to noise amplification for weak channel gain.However,computational complexity of LS estimator is less since it does not require prior channel statistics like in MMSE.MMSE estimator yields good results for signal detection and channel estimation as it utilizes the second-order statistics of the channel.However,perfect knowledge of the second-order statistics of the channel is difficult to get in practice.Thus,recently deep learning(DL)has emerged as a popular approach in many applications like channel estimation and signal detection in communication systems[7-8].Specifically,deep neural networks(DNN)have shown very good results in channel estimation,as they can learn and adapt to complex systems,unlike conventional LS and MMSE-based methods.

Related work: Refs.[8-10]have proposed a DNN-based OFDM system for joint channel estimation and symbol detection.The simulation results show that the proposed DNN yields result close to the more complex MMSE method.Recently a new approach called RoemNet[11],which utilizes meta-learning,has been introduced for channel estimation.This approach is more robust in learning channel information with fewer pilots.Furthermore,deep learning-based cyclicprefix(CP)free OFDM systems and index-modulated OFDM systems have been studied in Refs.[12-13].To estimate the channel,the super-resolution convolutional neural network (SRCNN) and denoising convolutional neural network(DNCNN)[7]are used,which consider the channel as a 2D image.The noisy image is treated as a low-resolution image,and SRCNN is used to increase its resolution,while DNCNN is used for image restoration.However,DL-based OFDM systems in Refs.[7-13]have not considered the effects of HIs on channel estimation and signal detection.

Performance of channel estimation and signal detection widely depends on the chosen algorithm.However,HIs significantly deteriorate the performance of an algorithm not designed to handle them[14].The hardware used in communication systems is associated with some impairments like phase noise,in-phase and quadrature-phase(IQ)imbalance,and amplifier nonlinearities[15-16].In practice,these impairments can limit the achievable performance of a system[9,17-20].HIs are prominent at higher frequencies in both the transmitter and the receiver,which can impact the performance of channel estimation and detection algorithms.In Ref.[21]authors have considered the HIs such as carrier frequency offset(CFO),direct current(DC)offset,and IQ mismatch.Effect of IQ mismatch and symbol error rate (SER) were discussed for single antenna multi-carrier,and multi-input and multi-output(MIMO)-OFDM systems[22].Effect of HIs has also been studied for beamforming design for MIMO OFDM systems[23].HIs do not only affect the bit error rate(BER)and mean square error (MSE) performance of the system but also affect the channel capacity.It has been observed that the channel capacity decreases with an increase in HIs[5].Therefore,it is necessary to deal with HIs to avoid degradation of a system’s performance.This paper proposes a DL-based OFDM system’s channel estimation and signal detection with HIs which are not considered or paid negligible attention in DL-based system design in the literature.For the sake of illustration,we explicitly contrast the contributions of this paper to other works on HIs performance analysis in Tab.1.

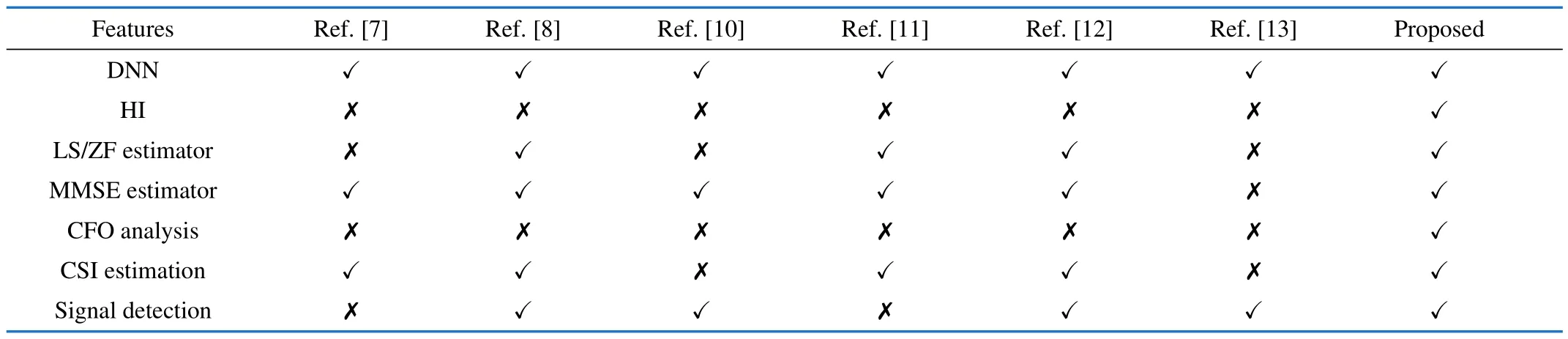
Tab.1 Contrasting our novelty to the existing techniques

We present the channel estimation and signal detection in the presence of HIs for the OFDM system using the DL.In the proposed DL-based OFDM system,(DL-OFDM),we use pilots’symbols to estimate the channel as a 2D image,which is then used for signal detection.The impact of various system parameters such as training signal to noise ration(SNR),channel models,number of pilots,and different HIs is used in system performance analysis.Results show that the HIs significantly affect the channel estimation and signal detection when the conventional LS/MMSE estimator is used,while the proposed DL-OFDM system is robust to them,exhibiting negligible impact on performance.Further,we observe that the proposed DL-OFDM exhibits good generalization ability and robustness to HIs’ variation.Further,the main contributions of the proposed work are summarized below.

•We present a novel channel estimation and signal detection technique in the presence of HIs for the OFDM system using DL model.

•Impact of various system parameters such as training SNR,channel models,number of pilots,and different HIs is analyzed.

•Performance of the conventional and the DL-based signal detector is evaluated under different channel conditions,and their performance is compared.

•We have conducted extensive simulation experiments to demonstrate the superior performance of proposed DLOFDM irrespective of HIs.

•Impact of channel variation from offine training to online signal detection is also considered to highlight the robustness of the proposed DL-OFDM.

The rest of the paper can be outlined as follows.In section II,the DL-OFDM system model is introduced,and the basic OFDM system is explained using the time-frequency frame.Section III analyzes HIs and their effects on the OFDM system performance.Channel estimation using conventional DL methods is discussed in section IV.Section V covers signal detection using the signal recovery neural network(SRNET).Section VI presents the results and discussion,and the paper concludes with section VII.

Notations:C denotes the set of all complex numbers.Bold-face upper-case and boldface lower-case letters are used to denote the matrices and the vectors respectively.The diag(h)notation represents a diagonal matrix with the main diagonal elements being the elements of vectorh.The complex conjugation ofxis denoted byx*.For a matrixX,XT,andXHrepresent the transpose and complex conjugate ofX,respectively.|Ψ|denotes the cardinality ofΨ.E[·]and‖·‖2denote the expectation and Euclidean norm of(·),respectively.

II.SYSTEM MODEL

A single antenna-based OFDM system is considered for DL-based channel estimation and signal detection,referred to as DL-OFDM,as shown in Fig.1.The DL-OFDM considers non-ideal hardware components at both the Tx and Rx such as IQ imbalance,carrier frequency offset,and DC offset.The proposed DL-OFDM system with HIs is shown in Fig.1.In Fig.1,the time-frequency grid of input data is shown,which consists of data and pilot symbols.The entire input grid is processed through a serial to parallel(S/P)converter and inverse discrete Fourier transform (IDFT) block to obtain an OFDM symbol with a CP in the time domain.The parallel time domain stream is passed through parallel to serial(P/S)converter and finally the CP is added to the transmitted signal.Due to system effect,IQ imbalance and the DC offset are added to the transmitted OFDM signal before it reaches the antenna,as shown in Fig.1.The CP is removed from the received signal after passing through the receiver IQ imbalance and DC offset HIs.Discrete Fourier transform(DFT)of the received signal is performed to get the signal back in the frequency domain.Due to the presence of HIs at both the receiver and transmitter,the received signal has an IQ mismatch.Channel estimation and signal detection are performed at the receiver end,using pilot symbols within the OFDM frame,with either LS/MMSE or DL-based methods.The LS method estimates the channel at pilot locations only,which may be noisy,and thus,is considered a low-resolution image.In order to increase the resolution of 2D channel image,SRCNN followed by feedforward DNCNN is used[7].The output of the DNCNN represents the estimated channel of the OFDM frame,which is then used for signal detection.The entire baseband receiver chain for channel estimation and signal detection is depicted in Fig.1.The DL-OFDM considersNssubcarriers andNdtime slots,where the received signal,after removing the CP and performing the DFT,can be represented as

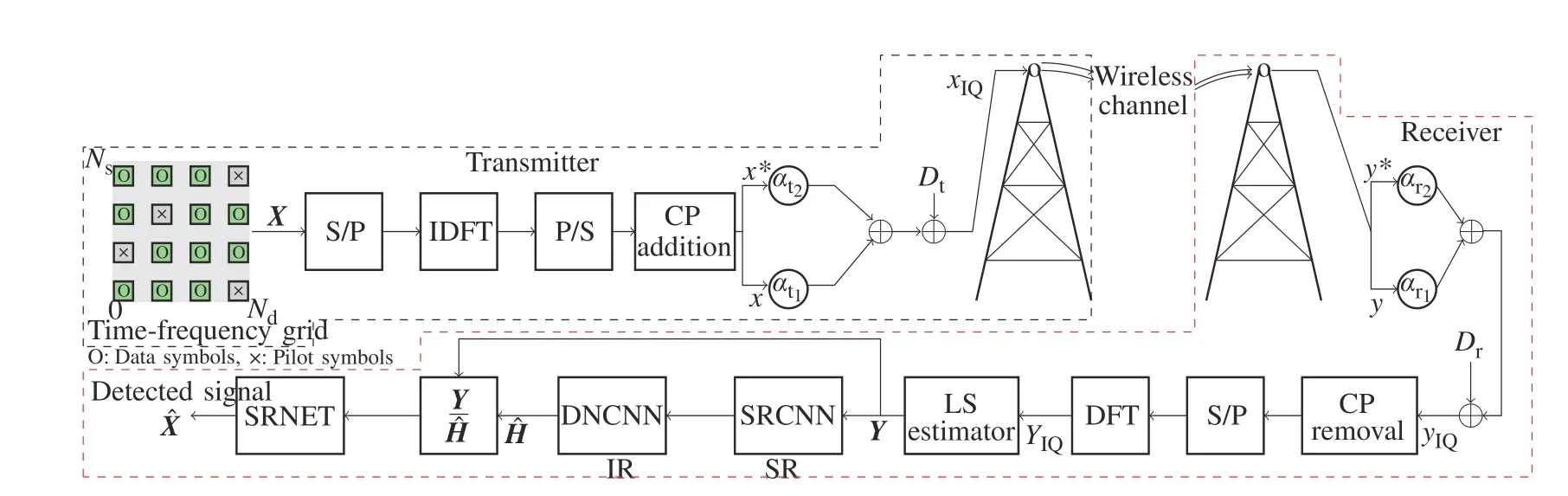
Fig.1 The DL-OFDM system model with HIs in system model X is the transmitted signal in the time-frequency domain. is the detected signal at the receiver using SRNET.The output of DNCNN denotes estimated channel for an OFDM frame. xIQ and yIQ are the impaired transmitted and received signal,respectively.SR and IR stand for the image super resolution and image restoration,respectively for channel estimation

III.HARDWARE IMPAIRMENTS

In practice,HIs are present in a system due to component mismatches and inaccuracies.These impairments,such as phase noise,high power amplifier (HPA) non-linearities,IQ mismatch,DC offset,CFO,and quantization errors,can degrade the performance of channel estimators and signal detectors in OFDM systems[15,21,24-25].Various techniques have been proposed in the literature to address the issue of HIs.However,these methods often fall short in terms of their effectiveness or have high computational complexity.

A.HIs at the Transmitter

The transmitted signalXm,nin(1)in the presence of HIs is written as

wherexIQ(t)is the time-domain impaired transmitted signal.αt1andαt2are asymmetrical IQ imbalance coefficients and they are given as[21]

wheregTandφTare transmitter gain and phase mismatch,respectively.x*(t)is the complex conjugate of the transmitted OFDM signalx(t).Dtdenotes a DC offset.Further,αt1+=1.Note that the system will be free from HIs ifgT=1,φT=0,andDt=0.

B.HIs at the Receiver

The received signalYm,nin (1) in the presence of HIs is given as

whereyIQ(t)is the time domain impaired received signal.αr1andαr2are asymmetrical IQ imbalance coefficients,and they are given as[21]

wheregRandφRare receiver gain and phase mismatch,respectively.Additionally,y*(t)represents the complex conjugate of the received OFDM signal andDrrepresents the DC offset at the receiver.To understand the effect of IQ imbalance only in system,(2)in the frequency domain at subcarrierfis expressed as

where-fdenotes the mirror subcarrier of thefth subcarrier.Similarly,the received signal in(3)is expressed as

The joint effect of the Tx and Rx IQ imbalance is represented on the received baseband signal by substituting(4)into(5)as

In the above equation,the first termand the second term(H(f)X*(-f))denote the attenuated transmitted signal and mirror interference,respectively.The third((-f)X*(-f)) and the forth ((-f)X(f))terms represent the combined Tx-IQ imbalance affected mirror interference in the received signalYIQ(f).Therefore,OFDM system performance degrades in the presence of IQ imbalance,as highlighted in the above expression.Further,the frequency spectrum illustration of the joint effect of Tx and Rx IQ imbalance is depicted in Fig.2.Thus,we get four copies of the actual signal in the received signal as shown in Fig.2.

Fig.2 Effect of IQ imbalance on the received signal when both Tx and Rx have IQ imbalance

1)CFO:The CFO is one of the major concerns in modern wireless communication systems.It arises when the received carrier frequency does not match the transmitted carrier frequency due to HIs at the transmitter and the receiver.The CFO can be calculated simply by taking the difference between the received carrier frequency and the transmitted carrier frequency as

whereΔ fdenotes the CFO,frandftdenote the received carrier frequency and transmitted carrier frequency,respectively.The received time-domain signal with CFO,yCFO(t),can be obtained by multiplying the received signaly(t)by the exponential term ej2πΔ ft,i.e.,yCFO(t)=y(t)ej2πΔ ft,which causes a shift in the received carrier frequency and results in CFO.

IV.CHANNEL ESTIMATION

In this section,the channel estimation in the DL-OFDM system is described.The conventional LS,MMSE,and the proposed DL methods are used for channel estimation for comparison.In DL-based channel estimation,the data set is divided into training and testing data.A trained DL-OFDM system is used for online signal detection.

A.Conventional Channel Estimation

The LS and MMSE are conventional methods used for channel estimation in the OFDM system.Nppilot symbols are inserted within an OFDM frame,and the collection of 2D pilot position indexes within the frame,denoted asΨp,has a cardinality of|Ψp|=Np.The channel coefficients at the pilot position are written as

wherempandnpdenote the pilot index at the sub-carrier and time-slot,respectively.

whererepresent the transmitted pilot symbols and noise,respectively.Vectored received signalypand pilot symbolsxpcan be calculated for all the pilot indexes.The LS channel estimation method computes the channel coefficients as a diagonal matrix and is given by

The LS channel estimator does not provide much accurate results when noise amplification happens due to poor channel condition or/and having any prior channel statistics.In such cases,the MMSE channel estimator is preferred over the LS estimator since it incorporates prior channel statistics and also does not affect due to noise amplification.The MMSE can be obtained by multiplying the channel response at pilot positions with the filtering matrix.Letbe the channel response at the pilot positions,and MMSE estimatoris expressed as

whereAMMSEis a filtering matrix and is given as

wherehdandhpare the channel coefficients at data locations and pilot locations respectively.are the cross-correlation of whole data with pilot points and autocorrelation of channel at pilot positions,respectively.σ2is the noise variance andxis the transmitted OFDM symbols.Mathematicallyare given as

The ideal MMSE estimator in (11) requires prior channel knowledge ofand SNR,which are unavailable in practice.Moreover,the MMSE needs matrix inversion,which has a computational complexity ofO().Hence,we propose a DL-based channel estimation for the OFDM system in the next section.

B.DL-Based Channel Estimation

In this work,we consider a single input and single output(SISO)OFDM system withNsfrequency sub-carriers andNdtime slots.The channel between the transmitter and receiver is modeled as a 2D image.First,we estimate the channel at pilot locations asusing the conventional LS method to obtain a low-resolution image,which may be noisy.The proposed channel estimation approach consists of two stages,namely SRCNN and DNCNN.The first stage involves using SRCNN to estimate the channel responseHfrom a lowresolution and noisy channel image,represented as a vector input.In the second stage,the image denoising network is used to remove the noise effects by cascading an image restoration (IR) network to a super-resolution (SR) network,where SRCNN and DNCNN are employed for image SR and IR,respectively[26-27].

1)Training of SRCNN and DNCNN:In order to train SRCNN and DNCNN,theΘdenotes the set of parameters of the network asΘ={ΘS,ΘR},whereΘSandΘRdenote the values of the parameters for the SR and IR networks,respectively.The cascaded SR and IR networks are used for channel estimation withas the input and the output estimated channel is denoted byfor an OFDM frame.The function performed by the entire system is denoted byf(·),and the estimated channel is given as

whereΘrepresents the set of parameters of SR and IR networks,anddenotes the channel response at the pilot locations.Moreover,(15)is expressed as

wherefSandfRare the functions performed by the SR and IR networks,respectively.The total loss function of the whole cascaded network is MSE between the estimated channel and the actual channel.To simplify the training process,a twostage training process is used.In the first stage,the MSE lossL1for the SR network is minimized as

where‖T‖is the size of training data,is the output of the SR network,andHis the actual channel response.In the second stage,the parameters of the SR network are kept constant,and the parameters of the denoising network are optimized by minimizing the loss functionL2given as

V.SIGNAL DETECTION

Signal detection in an OFDM system is performed using both conventional and DL approaches.A neural network is employed to decode transmitted symbols after estimating channel information from pilot symbols.The proposed DLOFDM system is divided into two parts: offine training and online testing.Results in the literature indicate that LS signal detection yields inferior results,which are further degraded by HIs.MMSE provides better results than LS,however signal detection also degrades with HIs,indicating that the LS and the MMSE are susceptible to HIs.

A.Conventional Signal Detection

The equalization of the received signal to recover the transmitted symbols is performed using the estimated channel state information in conventional signal detection.The postprocessing signal at the subcarriermand the time slotnis expressed as

Here,βis the regularisation parameter andIis the identity matrix.andYare the estimated channel and the received signal,respectively.

B.DL-Based Signal Detection

In this section,we propose a DL-based signal detection to recover the transmitted signal from the received signal conditioned on the channel state information.We have used a neural network for the recovery of the transmitted signal,which is named as SRNET.Detected symbolscan be expressed as

whereDSRNET(·)represents the signal recovery network havingγas the network parameters.Theis the estimated channel,andYis the received signal.The model is trained using an estimated output signal,which is obtained from the received signal and known channel statistics.The SRNET used in this work comprises of four convolutional layers with 500,30,10,and 2 units of neurons,respectively1Using extensive simulation,we set these parameters by considering performance and complexity trade-off..The first,second,and third convolutional layers use a sigmoid activation function.The sigmoid activation function is given asfS(a)=1/(1+e-a).The output layer utilizes the soft-max function as an activation function given by softmax(zi)=whereKis the number of classes in the classifier.SRNET specifications are also mentioned in Tab.3.During training,the loss function between the actual output and the SRNET output is minimized.Common loss functions include MSE,Kullback-Leibler distance,and cross-entropy.In this work,we use the cross-entropy loss function since the input and output are in bit form.The loss function is written as

wherexiis the original transmitted symbol withi ∈{1,2,···,m}andis the estimated symbol probability at the DL receiver.The loss functionLis minimized using a training data set.Once the SRNET model is trained,it is used for online signal detection in the OFDM system,and the BER is calculated by comparing the output values and actual values.

VI.RESULTS AND DISCUSSION

In this section,we present the performance results of channel estimation and signal detection both with and without HIs.The MSE and BER are used as performance metrics, and we compare the results obtained using the proposed DLOFDM with the commonly used LS/MMSE algorithms.For signal detection,the binary phase-shift keying (BPSK) and quadrature phase-shift keying(QPSK)modulation techniques are used.Further,the size of one OFDM frame is taken asNs×Nd.HereNs=72 andNd=14 are used as the number of sub-carriers and time slots,respectively.Furthermore,48 pilots are used in each OFDM frame.

A.SRCNN and DNCNN Parameters

To increase resolution of the channel image,we first interpolate it and then use a three-layered CNN to increase its resolution.Each layer uses ReLU as its activation function.The first layer uses 64 filters of size 9×9,the second layer uses 32 filters of size 1×1,and finally,the output layer uses a single filter of size 5×5 to reconstruct the image(channel).For image restoration or image denoising,DNCNN[27]consists of 20 convolutional layers.The first layer consists of 64 filters of size 3×3×1 with a ReLU activation function.The output layer consists of a single filter with a size of 3×3×64 to reconstruct the output.The 18 intermediate convolutional layers consist of 64 filters of size 3×3×64 with ReLU activation function.Tab.2 lists the parameters for SRCNN and DNCNN.Further,the parameters for signal detection and HIs such as IQ mismatch,DC offset,and CFO are mentioned in Tab.3 and Tab.4,respectively.

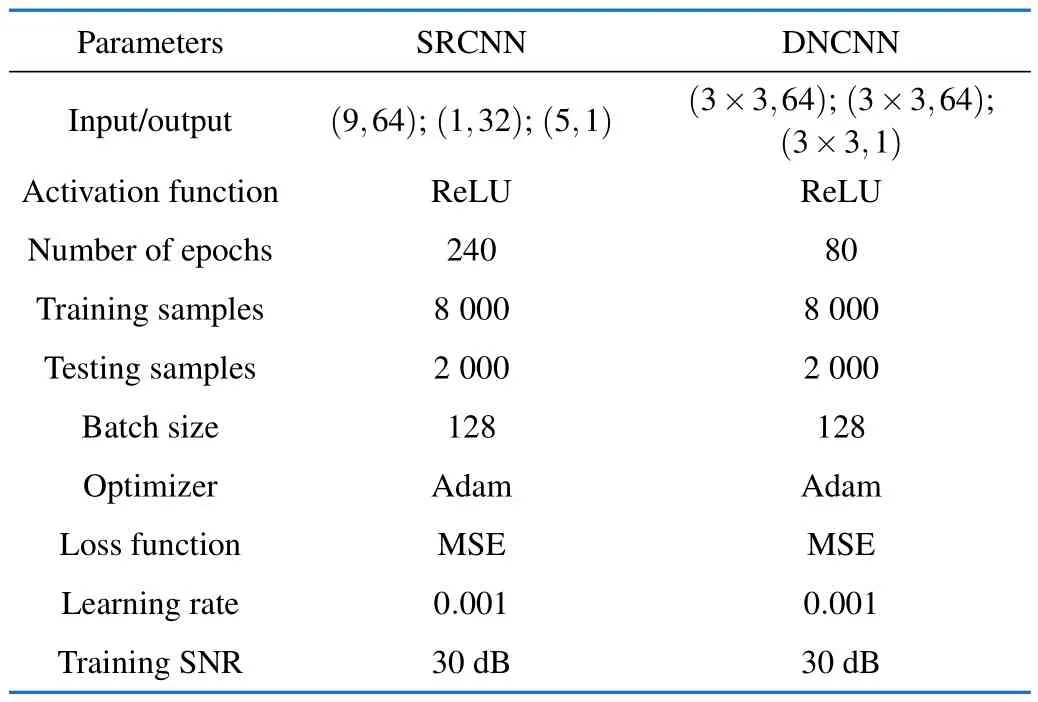
Tab.2 SRCNN and DNCNN parameters for channel estimation

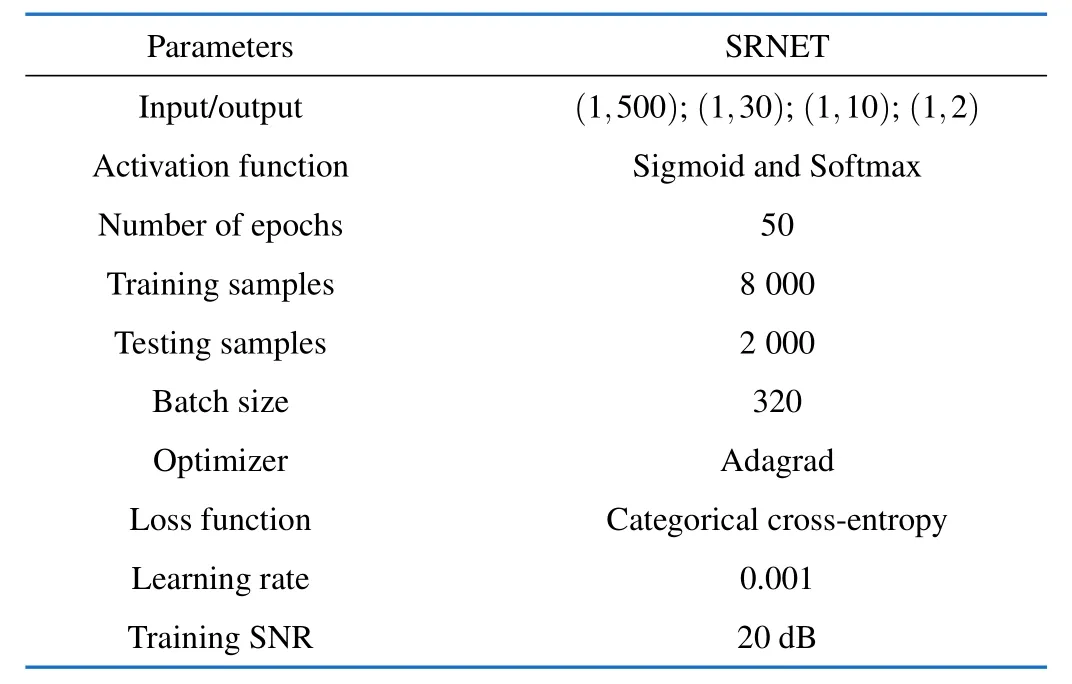
Tab.3 SRNET parameters for signal detection

Tab.4 Hardware impairments

Fig.3 depicts the MSE vs SNR performance of channel estimation with and without HIs.Results show that the proposed DL-based channel estimator is less affected by HIs compared to the LS or the MMSE detector.The MSE performance of LS or MMSE deteriorates by approximately one decibel due to IQ mismatch and DC offset impairments,as observed in Fig.3.

Fig.3 MSE vs SNR performance of OFDM system in vehicular channel model[7]with and without HIs

Average BER performance is shown in Fig.4 in the presence of HIs.It is observed that the BER performance of LS or MMSE algorithms deteriorate(around 6 dB at BER=10-4),whereas DL-based detection shows almost similar results with and without HIs,as shown in Fig.4.

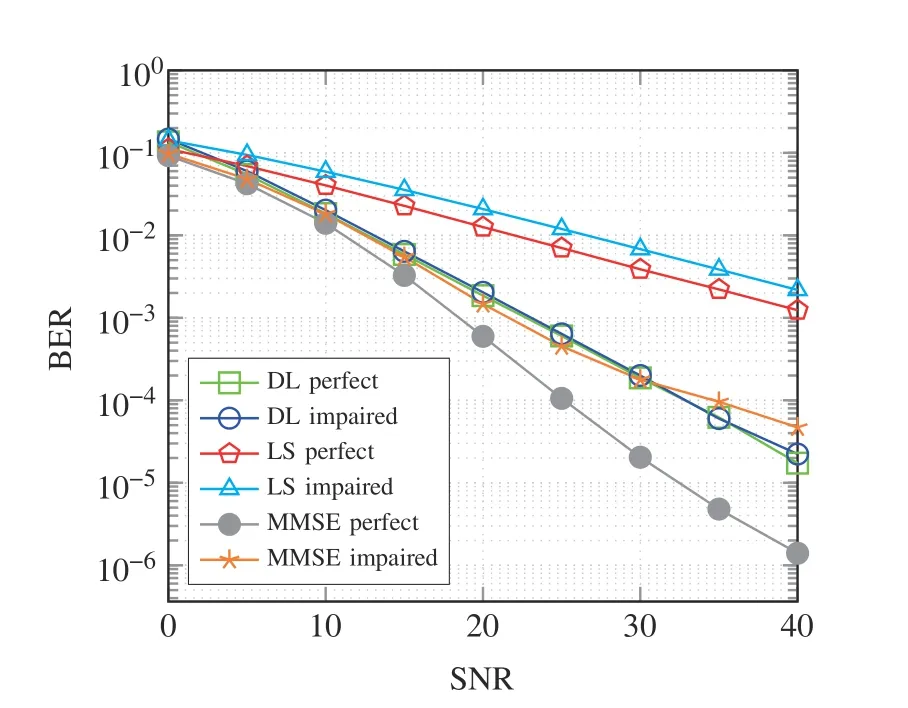
Fig.4 Average BER performance in Rician channel model in presence of IQ mismatch and DC offset at receiver

In the presence of a CFO,the average BER performance of OFDM system is shown in Fig.5.It is observed that the presence of a CFO affects BER performance significantly(around 15 dB at BER=10-3)in case of LS or MMSE algorithms as compared to the DL-based detection,as observed in Fig.5.

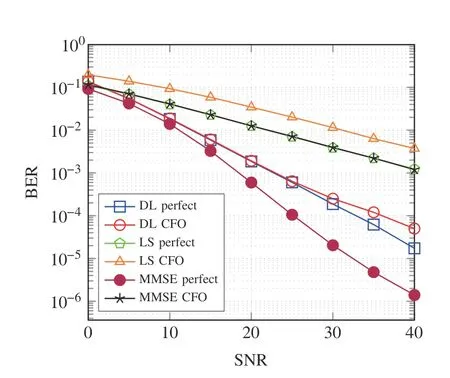
Fig.5 Average BER performance in Rician channel model in presence of CFO

Fig.6 shows the BER performance as a function of SNR in the presence of HIs,including IQ mismatch,DC offset,and CFO.It can be observed that the DL-based detection is minimally affected by the HIs,as evidenced by the relatively constant BER performance across different SNR levels,as shown in Fig.6.On the other hand,LS or MMSE algorithms exhibit a noticeable degradation in BER performance,with an error foor in signal detection at high SNR levels in the presence of HIs,as observed in Fig.6.

Fig.6 Average BER performance in Rician channel model in presence of CFO,DC offset,and IQ mismatch

Fig.7 shows average BER performance with SNR for a QPSK modulation scheme in the presence of HIs.The HIs have a negligible effect on DL-based signal detection,as shown in Fig.7.Further,it is clearly visible in Fig.7 that in the presence of HIs,BER performance of LS or MMSE algorithms show a greater deterioration as the order of modulation scheme increases in signal detection.

Fig.7 Average BER performance of QPSK modulation in the Rician fading in presence of CFO,DC offset,and IQ mismatch

The above results show that the performance of the traditionally used method for channel estimators and signal detectors deteriorates when HIs are taken into account.The MMSE method exhibits better performance without HIs,but it has a high complexity and requires second-order channel statistics,as shown in the results.By varying the parameters associated with HIs such asgT,gR,φT,φR,Dt,andDr,we have observed that the performance of LS and MMSE estimators also varies.Further,DL-based OFDM design is more resilient to HIs compared to conventional LS or MMSE methods.

Fig.8 shows comparison of BER vs SNR performance of the proposed DL-based signal detector and conventional LS and MMSE detectors,considering the presence of HIs and utilizing the extended vehicular A(EVA)channel model.The results in Fig.8 clearly demonstrate the superior performance of the DL-based signal detector over the conventional detectors.For example,DL detector has around 5 dB at BER=10-3gain compared to MMSE in the presence of HIs under EVA channel model.The simulation parameters of the EVA channel model are shown in Tab.5.

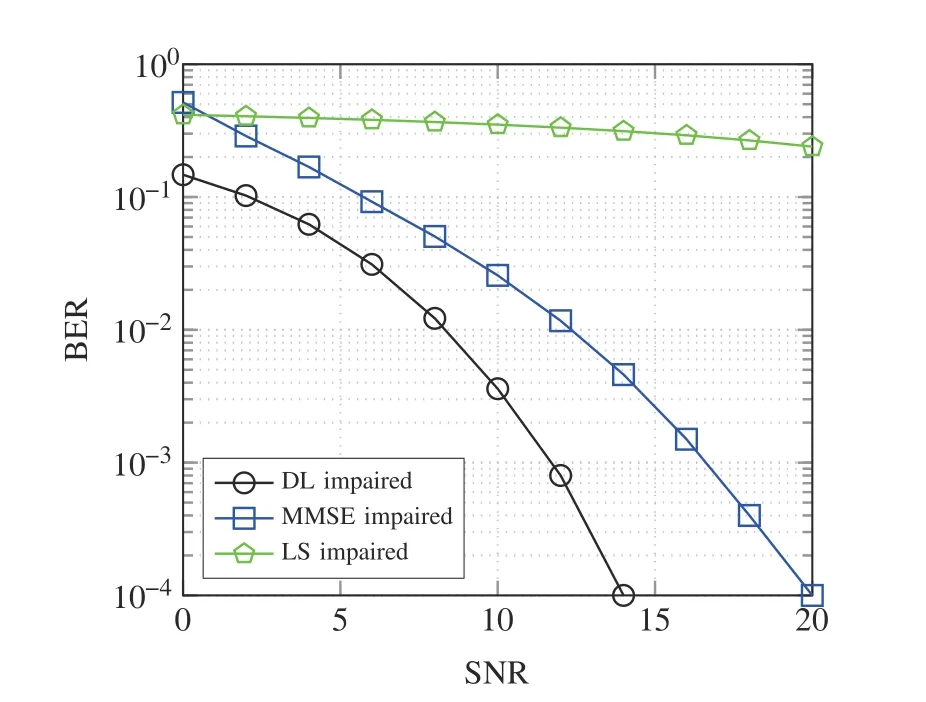
Fig.8 Average BER performance of QPSK modulation in the EVA channel model in the presence of CFO,DC offset,and IQ mismatch

Tab.5 EVA channel parameters

Robust Analysis: We have considered that the channel varies from offine training to online testing for the robust analysis of the DL-OFDM system.Channel variation can be modelled as

wherehonlineandhoffinedenote the online and offine channel coefficients,respectively.e～C N(0,) is the channel variation.Thecan be modeled in terms of the channel variance,i.e.,=,whereis the channel variance.BER performance of DL-OFDM in EVA channel is shown in Fig.9 by considering channel variation from offine training to online testing.We observe that the variation in the channel statistics does not degrade MSE performance significantly.

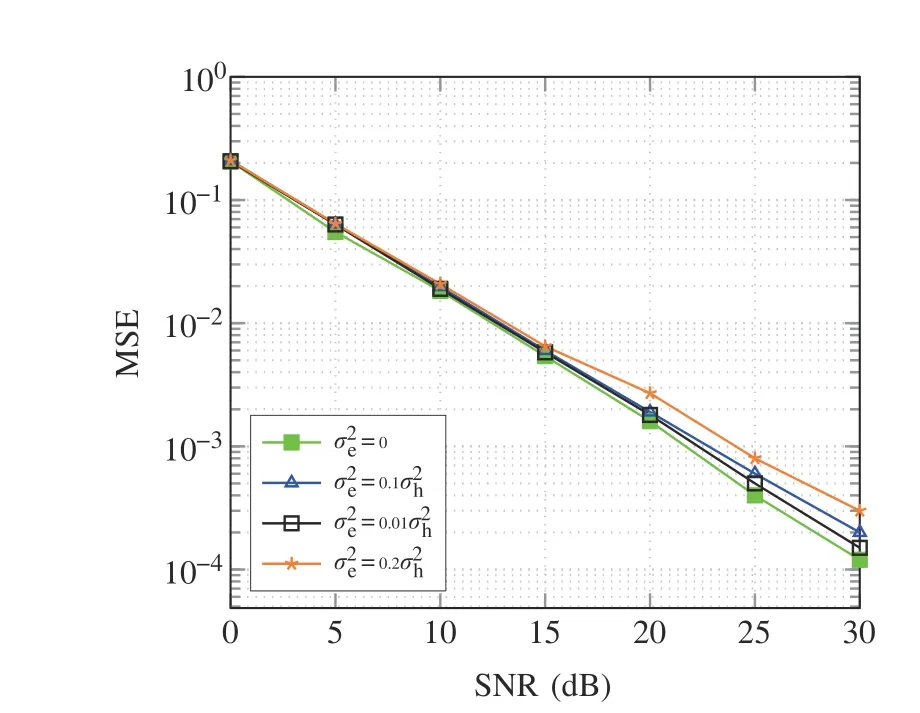
Fig.9 BER vs SNR performance of DL-OFDM in standard EVA channel model by considering channel variation

Fig.10 shows the BER vs SNR performance of different DL-based signal detection models.From Fig.10,it is evident that the proposed model outperforms the other DNN-based signal detector[8].

Fig.10 BER vs SNR performance of different DL-based signal detectors over Rician channel model

Computational Complexity: For channel estimation,we have used LS and MMSE channel estimators including DLbased estimators such as SRCNN and DNCNN.The processing time for SRCNN to handle one 72×14 channel frame is 0.27 ms,while DNCNN takes 0.72 ms to handle the same size frame.Therefore,DL-based channel estimation requires a total of 0.99 ms.On the other hand,traditional channel estimators like LS and MMSE have a higher time complexity than DL-based estimators.LS takes 6 ms to process a single channel frame of size 72×14,and MMSE takes 0.03 s to process a single frame of the same size channel.

Computational complexity of SRCNN and DNCNN mainly depends on the number of layers,number of filter in each layer,and size of input image here we are taking size of input image as the size of OFDM frame.DNCNN requires more layers due to extra batch normalisation layers the computational complexity of DNCNN slightly increases.The order of complexity for each layer of SRCNN and DNCNN is mathematically expressed as follows: Let the size of OFDM frameNf×Ns,whereNfis number of sub-carriersNsis number of time slots,and letCiandCorepresents the number of input and output channels,and letK×Kbe the filter size.Then the order of complexity of each layer can be modeled asO(Nf×Ns(Ci×Co)(K×K)).As SRCNN and DNCNN use same size convolutional layers hence the computational complexity mainly depends on the product of number of subcarriers and number of time slots,hence these model have linear computational complexity as shown in Tab.6.

Tab.6 Computational complexity

VII.CONCLUSION

The paper focused on channel estimation and symbol detection using deep learning,both with and without HIs.The proposed SRNET model is trained offine and then uses for online signal detection that views wireless channels as a black box.Simulations show that the deep learning has an advantage when the transmitter and the receiver are hardware-impaired.The performance of the SRNET method is good both with and without HIs,indicating that SRNET can learn and remember the characteristics of complex wireless channels.Further,we have added different HIs to the transmitter and receiver and have found that the deep learning method gives better BER and MSE performance as compared to LS and MMSE.Additionally,the results show that the performance of LS and MMSE algorithms degrades significantly when the modulation order increases in the presence of HIs,while the SRNETbased detection is only slightly affected.In the near future,more rigorous experiments can be conducted to analyze the impact of residual impairments present in the transmitter and receiver.