Resource Allocation for URLLC with Parameter Generation Network

Jiajun Wu,Chengjian Sun,Chenyang Yang

Abstract—Deep learning enables real-time resource allocation for ultra-reliable and low-latency communications (URLLC),one of the major use cases in the next-generation cellular networks.Yet the high training complexity and weak generalization ability of neural networks impede the practical use of the learning-based methods in dynamic wireless environments.To overcome these obstacles,we propose a parameter generation network (PGN) to efficiently learn bandwidth and power allocation policies in URLLC.The PGN consists of two types of fully-connected neural networks (FNNs).One is a policy network,which is used to learn a resource allocation policy or a Lagrangian multiplier function.The other type of FNNs are hypernetworks,which are designed to learn the weight matrices and bias vectors of the policy network.Only the hypernetworks require training.Using the well-trained hypernetworks,the policy network is generated through forward propagation in the test phase.By introducing a simple data processing,the hypernetworks can well learn the weight matrices and bias vectors by inputting their indices,resulting in low training cost.Simulation results demonstrate that the learned bandwidth and power allocation policies by the PGNs perform very close to a numerical algorithm.Moreover,the PGNs can be well generalized to the number of users and wireless channels,and are with significantly lower memory costs,fewer training samples,and shorter training time than the traditional learning-based methods.

Keywords—URLLC,resource allocation,hypernetworks,deep learning

I.INTRODUCTION

Ultra-reliable and low-latency communications(URLLC)can support mission-critical applications such as intelligent transportation,autonomous driving,and smart grid[1],where resource allocation is critical for ensuring the stringent quality-of-service (QoS) with limited bandwidth[2-6].Since the resultant optimization problems are usually non-convex and sometimes without models,machine learning has been introduced to find resource allocation policies that can be implemented with low computing latency[7-9].

While learning-based methods have been shown promising in facilitating real-time resource allocation,they still face two bottlenecks that hinder their practical use in wireless communications: high training complexity and weak generalization ability[10].Due to the dynamic propagation environments and fuctuating traffic load,the test scenarios of a learned resource allocation policy usually differ from the scenarios gathering samples for training a deep neural network(DNN).Most existing DNNs cannot be generalized to unseen scenarios,especially the unseen problem scales.As a result,whenever the environment changes,the DNN needs to be re-trained for adapting to new scenarios,which makes the computing latency of the learning-based methods still unacceptable for URLLC.

A straightforward approach to avoid re-training is to train a “versatile” DNN with all samples gathered from every possible scenario,which however incurs huge training cost,i.e.,large number of training samples and long training time.

To learn efficiently in new environments,hypernetwork was proposed in Ref.[11],which trains a small neural network to generate the weight matrix of another DNN.This approach has been recently introduced into intelligent wireless communications[12-13].In Ref.[12],a hypernetwork was designed to generate the weight matrix of a DNN for optimizing signal detection,which takes the channel matrix as the input.In Ref.[13],hypernetworks were designed to generate the weight matrices of the DNNs for leaning channel estimation and beamforming policies,which take the received signals as the inputs.However,the input dimensions of the hypernetworks designed in Refs.[12-13]increase with the problem scales (e.g.,the number of users or antennas),resulting in a substantial rise in the training cost.

In this paper,we strive to reduce the computing latency of optimizing resource allocation among users for URLLC by designing DNNs with low training complexity and strong generalizability.In URLLC,the QoS requirement of each user can be characterized by an end-to-end(E2E)delay bound for each packet and the overall packet loss probability.For wireless access systems,the E2E delay is composed of the time required by uplink and downlink transmission,signaling,computing,and queuing as well as backhaul.The overall reliability requirement is composed of the decoding error probability and the queuing delay violation probability in uplink and downlink.We consider a downlink system and take the power and bandwidth problem that minimizes the total bandwidth required by ensuring the QoS of every user as an example.

To learn the power and bandwidth policies with high efficiency,we propose a parameter generation network (PGN)for learning resource allocation.The PGN consists of two types of neural networks: a policy network for learning a resource allocation policy or a Lagrangian multiplier function(used for controlling the QoS),and hypernetworks for learning the weight matrix and bias vector (referred to as weights for short)in every layer of the policy network.

The major contributions are summarized as follows.

•We propose a PGN for optimizing resource allocation in URLLC.Unlike previous studies[11-13],the designed hypernetworks take the indices of the weights of the policy network as inputs,and the designed policy network is with data preprocessing and post-processing (specifically,ranking).Because the indices do not change with problem scales and lead to small input sizes of hypernetworks,the number of trainable parameters of the hypernetworks is small and the overall training cost of the PGN is low.

•Simulation results demonstrate the benefits of the proposed PGNs for learning the power and bandwidth allocation policies.Specifically,the PGNs can satisfy the stringent QoS of all users in the system and can be well generalized to the number of users and wireless channels.Furthermore,the PGNs require much lower memory,much shorter training time,and much fewer training samples than the traditional learning-based methods to achieve the same system performance.

The rest of the paper is organized as follows.In section II,we introduce the system model,the resource allocation problem for URLLC,and its primal-dual form for learning the resource allocation policies with ensured QoS.In section III,we introduce the structure and training procedure of the PGN and show how to learn the resource allocation policies with PGNs for URLLC.In section IV,we evaluate the performance of the PGNs.Section V concludes the paper.

II.LEARNING TO OPTIMIZE POWER AND BANDWIDTH ALLOCATION

In this section,we introduce the system model,the power and bandwidth allocation problem for URLLC,and the unsupervised learning method for optimizing the power and bandwidth allocation policies with ensured QoS.

A.System Model

We consider a downlink multi-antenna orthogonal frequency division multiple access (OFDMA) system for supporting URLLC,where a base station (BS) withNtantennas servesKsingle-antenna users.The maximal transmit power of the BS isPmax.

The packets for each user arrive at the buffer of the BS randomly.Since the inter-arrival time between packets may be shorter than the service time of each packet,the packets may have to wait in the buffer.We consider a queuing model that the packets for different users wait in different queues and are served in a first-come-first-serve manner.

To facilitate low transmission latency,we consider a short frame structure.The duration of each frame isTf,which consists of a durationτfor transmission and a duration for signalling(say sending pilots for channel estimation).Since the E2E delay requirement of URLLC is typically shorter than the channel coherence time,the small-scale fading channel is quasi-static and time diversity is not useful.

To improve the transmission reliability within the delay bound,we consider frequency diversity,by assigning different subcarriers in adjacent frames to different users.When the frequency interval between adjacent subcarriers is larger than the channel coherence bandwidth,the small-scale channels of a user among frames are independent.Since the packet size in URLLC is usually small,the bandwidth required for transmitting each packet is less than the coherence bandwidth,i.e.,the small-scale channel is fat fading.We do not assume any distribution for small-scale channels,since learning-based methods are applicable to any channel statistics.

Due to the short transmission duration,the blocklength of channel coding is short,and hence the impact of decoding errors on reliability is non-negligible.In order to characterize the probability of decoding errors,we consider the achievable rate in finite blocklength regime.In quasi-static fat fading channels,when the small-scale channel coefficient is available at the BS and each user,the achievable rate of each user(say thekth user)can be accurately approximated by[16]

B.Power and Bandwidth Allocation Problem

Denote the E2E delay bound asDmax.We only consider downlink delay,given that the delay components of uplink transmission and processing as well as backhaul have been studied in literature[7]and can be subtracted from the E2E delay.In particular,Dmaxconsists of the queuing delay at the BS(denoted asDqkfor thekth user),downlink transmission delayDtand decoding delayDc.

Effective bandwidth and effective capacity have been widely used to analyze the tail probability of queuing delay[14-15].The effective bandwidth of a packet arrival process is the minimal constant packet service rate that is required to guarantee the delay bound and the delay bound violation probability[15].Effective capacity of a packet service process is the maximal constant packet arrival rate that can be supported by the service process subjected to the requirements on the delay bound and the delay bound violation[14].Effective bandwidth depends on the statistics of packet arrival.Effective capacity refects the service ability of a system for a user with QoS exponent,which depends on the required queuing delay and delay bound violation probability[2].As analyzed in Ref.[2],ifTf≪Dmax,which is true in URLLC,effective bandwidth and effective capacity can be used to analyze the queuing delay at the BS for Poisson,interrupted Poisson,and switched Poisson arrival processes.

We take the Poisson arrival process with the average packet arrival rateakpackets/frame as an example,whose effective bandwidth can be expressed as[2]

Since the small-scale channel gains of a user are independent among frames with the considered frequency diversity,the effective capacity of thekth user can be expressed as[8]

To improve the resource usage efficiency,the power and bandwidth allocation are optimized to minimize the total bandwidth required by satisfying the QoS of every user,

The constraints in (4a) refect the QoS requirements of all users.The QoS of each user,characterized byDmaxandεmax,can be satisfied if(4a)holds after substituting the expression ofskin (1) into (3).The constraints in (4b) and (4c) are the power and bandwidth constraints.

The problem seems simple but is hard to solve due to the constraint in (4a).First,the constraint cannot be expressed in closed-form in general case,due to the expectation taken over small-scale channel gains for obtaining effective capacity.Only in a special case of large-scale antenna systems under Rayleigh fading channels,the effective capacity and hence the QoS constraint has a closed-form expression[18].Second,the achievable rate within the effective capacity is non-convex.

As a result,the optimal solution of this problem cannot be obtained by using standard convex optimization tools.Fortunately,the problem is quasi-convex as proved in Ref.[19].Therefore,stochastic gradient descent (SGD) method can be used to find the optimal solution for each given value of the environmental parameter.However,the SGD method requires a large number of iterations for satisfying the stringent QoS constraint.To reduce the resulting high complexity and thus long computing delay,we resort to DNNs for learning the power and bandwidth allocation policies.

C.Learning Power and Bandwidth Allocation Policies

A resource allocation policy is the mapping from environmental parameters to the optimized resource.From the expressions in(1)and(3),we can see that the effective capacity of thekth user depends onαk,and hence the environmental parameters areα1,···,αK.Then,the power allocation policy can be expressed asP(α)≜[P1(α),···,PK(α)]and the bandwidth allocation policy can be expressed asB(α)≜[B1(α),···,BK(α)],whereα≜[α1,···,αK].

The DNNs for learning the two policies can be trained in a supervised or unsupervised manner.When using supervised learning,a large number of labels should be obtained by solving the optimization problem and the QoS constraints are hard to be satisfied.To control the QoS and avoid the need of generating labels,we resort to unsupervised learning.

To learn the policies without supervision from the constrained variable optimization problem in (4),one can first transform the problem into its primal-dual problem and then transform the primal-dual problem into the following functional optimization problem[8],

The first transformation is equivalent if the problem in(4)is convex and the Slater’s condition holds.The second transformation is always equivalent as proved in Ref.[8].

Then,the DNNs for learning the functionsP(α),B(α)andλ(α)≜[λ1(α),···,λK(α)]can be respectively trained by minimizing and maximizingEα{L(α,Pk(α),Bk(α),λk(α))by replacingEα(·)as the empirical average over the samples of the large-scale channel gainsα.

III.PARAMETER GENERATION NETWORK

In this section,we first introduce the structure and training procedure of a PGN.Then,we show how to apply the PGNs for learning the power and bandwidth allocation policies.

A.Structure Design

A PGN consists of two types of neural networks,as shown in Fig.1.One is a policy network for learning a functionF(α),denoted asP(α;W,b),whereWandbare the weight matrix and bias vector.The other type of neural networks are hypernetworks for learning the weights in the policy network.In the proposed PGN,the hypernetworks learn the mappings from the indices of elements inWandbto the values of the elements.Both types of neural networks can simply be fully-connected neural networks(FNNs).

1) Policy Network:The policy networkP(α;W,b) is used to learn a multivariate functionF(α)=[f1(α),···,fK(α)],whose input feature isα,and the output is≜[,···,].

The output of thelth layer in the policy network for learningfk(α)is

We can introduce two hypernetworksW l≜W l(k,j;θWl)andBl≜Bl(k;θbl) to learn the mapping fromk,jtoWlk,jand the mapping fromkto,respectively,whereandθblare trainable parameters.Once the hypernetworks are welltrained,is obtained by inputtingk,j=1,···,KintoW landis obtained by inputtingk=1,···,KintoBl,respectively,all via forward propagation.In this way,the weights in the policy network,Wandb,can be obtained.

Since only two FNNs are used to generate the weight matrix and bias vector of each layer of the policy network,2(NL+1) FNNs are required to generate all the weights of the policy network withNLhidden layers.

3) Pre-Processing and Post-Processing:According to Fig.8 in Ref.[11],the weight matrix of the neural network generated by the hypernetworks behaves similarly to the weight matrix of a convolutional neural network(CNN)when the indices of the weights of the policy network are inputted into the hypernetworks.Specifically,the weight matrix of the generated neural network has a property of local smoothness1A matrix(or a vector)has the property of local smoothness if the adjacent elements of the matrix(or the vector)have similar values[21].,which is a property of the weight matrix of a CNN[20].Nonetheless,it was shown in Ref.[11]that the hypernetworks with indices as input do not perform well.This is because the inputs of the policy network therein do not exhibit any local smoothness property.

It is well-known that CNNs are successful in the tasks when the inputs are images,which are locally smooth.Inspired by such an observation,we pre-process the input featureαof the policy network such that the input feature is locally smooth.

For the functions that need to be learned in the problem at hand,i.e.,P(α),B(α),andλ(α),the adjacent elements inαare the large-scale channel gains of different users.Since the users are randomly located,their large-scale channel gains are far from similar.Fortunately,the input feature vectorαwill become locally smooth after using a simple data preprocessing: ranking,meanwhile the multivariate functionsP(α),B(α),andλ(α) remain unchanged after ranking,which amounts to the re-numbering of the users.

In particular,we can rank the elements inαin the ascending (or descending) order before inputting it into the policy network.To avoid changing the functionP(α),B(α),orλ(α) to be learned,the output of the policy network should also be ranked in the ascending(or descending)order.

Denoteαsas the ranked input feature according to the ascending order,i.e.,≤≤···≤.From Theorem 10.3 in Ref.[22],it is not hard to obtain the following corollary2When the elements in α are ranked according to descending order,a similar corollary can be obtained under the same condition in Corollary 1,where.

Corollary 1Ifαk,k=1,···,Kare independent and identically distributed andK →∞,then

B.Training Procedure

Only the hypernetworks in a PGN need to be trained,but the policy network is also involved during training.The forward and backward propagation procedure of one layer is shown in Fig.2.

Fig.2 Forward(black solid line)and backward propagation(red dash line)for one layer of the PGN,where ∇xy denotes the gradients and L(·)denotes the loss function,respectively

C.Learning Power and Bandwidth Policies

We employ three PGNs to learnP(α),B(α),andλ(α),respectively.

In order to satisfyBk≥0 andλk≥0 in(5),softplus function(i.e.,y=log(1+ex))is used forPBandPλ.

To enhance the adaptability of the PGNs to dynamic environments,we resort to the method proposed in Ref.[23],where the output ofPPis activated by Softmax function and the output ofPBis activated by a pre-trained function used for learning the scaling law ofB(α)withK.

The hypernetworks in the three PGNs are trained jointly using Algorithm 1.The loss function can be obtained from the objective function of the problem in (5),where the expectation inEα(·)and in the effective capacity are estimated by the empirical mean from the samples ofαandg=[g1,···,gK],respectively.

IV.SIMULATION RESULTS

In this section,we evaluate the performance of the proposed PGNs for learningP(α),B(α),andλ(α)in URLLC.

We compare the PGNs with the DNNs that are not generated by hypernetworks,and a numerical method as follows.

•FNNs-NoH[8]:P(α),B(α),andλ(α) are learned by three FNNs trained by the samples without ranking.Despite that the problem in(4)is not the same as that in Ref.[8],but the basic idea of the method in Ref.[8]can be used to help solve the problem in(4).

•CNNs:P(α),B(α),andλ(α) are learned by three CNNs trained by the samples without ranking.

•SGD: This method finds the optimal power and bandwidth allocated to users using SGD algorithm for each given value ofα.

A.Simulation Setting

In the simulation,the small-scale channels are subject to Rayleigh fading.The large-scale channels are generated according to the path loss model 35.3+37.6log(dk),wheredkis the distance between thekth user and the BS.All users are randomly located in a cell with the radiusR=250 m,whose minimal distance from the BS is 50 m.

When the parameters such asPmax,Nt,τ,andTfchange,similar results can be obtained and hence are not provided.

B.Sample Generation and Hyper-Parameters

A sample is a realization of the small and large-scale channel gains of all users,i.e.,(g,α).In each realization,gis randomly generated from Rayleigh distribution andαis generated according to the path loss model and user location mentioned in the simulation setting.

For training the hypernetworks in each PGN,the samples are ranked according to the ascending order ofα,which is denoted as(gs,αs).Considering that the values ofαare usually small,we scale them as log(α)+30 to accelerate training.

The fine-tuned hyper-parameters of all DNNs are shown in Tab.1,where [*l,*2,···,]denotes that there are*lneurons (for FNN) or*lchannels (for CNN) in thelth layer,Leaky ReLU denotes the functiony=xifx≥0 andy=0.01xotherwise.

Tab.1 Hyper-parameters for the DNNs

C.Performance Metrics

We use availability[24]and total bandwidth as the metrics for evaluating the system performance of the learned policies for supporting URLLC.

Availability refects the percentage of the users with satisfied QoS among all the users in the system.Total bandwidth is the sum of the bandwidth of all users required by a learned or optimized policy.They are respectively defined as

whereNdenotes the set of the test samples,εkandare the achieved packet loss probability and the allocated bandwidth of thekth user by a learned or optimized policy.

To achieve a near-optimal performance,the system performance is obtained by selecting the best PGNs from 10 times training,each with randomly generated training samples and randomly initialized hypernetworks.

Since the expectations are estimated by the empirical mean,the learned policy is unable to satisfy the originally required value ofεmaxwith probability one.To ensure the QoS of every user,we use the conservative design method in Ref.[8],where a more stringent reliability requirement thanεmaxis set during training,i.e.εD ＜εmax.To ensure an availability of 1.00 for the cases where the training and test samples are generated in the same scenario,the values ofεDfor the PGNs,FNNs-NoH and the CNNs are respectively 6×10-6,5×10-6,and 5×10-6,which are obtained from simulations.

D.Learning Performance

In practice,the number of users and the large-scale channel gains may change rapidly due to user scheduling and user mobility.Therefore,the generalization ability to the dynamic user population and channel statistics are important for wireless resource allocation.

To evaluate the generalizability to the number of users,the training and test sets for different DNNs are generated according to Tab.2,where the training samples for PGNs,FNNs-NoH,and CNNs are generated in a 10-user system while the test samples are generated in the systems with 5, 10, 20,or 50 users.When generating the test set,100 samples are generated for each value ofKin[5,10,20,50].

Tab.2 Training and test sets

We also compare the PGNs with three “versatile FNNs” for learningP(α),B(α),andλ(α) (with legend “FNNs-NoH*”).Each versatile FNN in FNNs-NoH*is trained by the samples with all possible values ofK,where the input feature vector is of size 50.WhenK ＜50 in the test set,the input feature vector of each FNN is padded with zeros.60 000 samples are generated for eachKin[5,10,20,50].The hyperparameters for each versatile FNN are the same as the FNNs-NoH.

The system performance of all methods is shown in Tab.3.Since FNNs-NoH is trained by the samples withK=10(i.e.,the input feature vector is of size 10),they cannot be tested in the scenarios withK ＞10.We can see that only in the test scenario withK=10,PGNs,FNNs-NoH,and CNNs are with similar system performance.For other test scenarios,either the availability achieved by the policies learned by FNNs-NoH and CNNs is lower than 1.00 or the total bandwidth required by the policies learned by FNNs-NoH and CNNs is much larger than PGNs.Besides,the policies learned by PGNs and FNNs-NoH*achieve almost the same system performance as SGD in all the test scenarios.This indicates that PGNs can learn the power and bandwidth allocation policies well and can be generalized to the number of users.

Tab.3 Generalizability to the number of users

According to the simulation setup,the large-scale channel gains are determined by the user’s locations,which follow a uniform distribution with BS-user distancedk ∈[50,R].When the cell radiusRchanges,the distribution of the large scale channel gains changes.To evaluate the generalizability to channels,the training and test sets are generated according to Tab.4,whereR=250 m in the training set for PGNs,FNNs-NoH and CNNs andR=100 m,250 m,300 m,and 500 m in the test set.When generating test set,100 samples are generated for eachRin[100,250,300,500]m.We also consider the “versatile FNNs” trained by the samples with all possibleR,i.e.,FNNs-NoH*,for comparison,where 50 000 samples are generated for eachRin[100,250,300,500]m.

Tab.4 Training and test sets

Since similar results can be obtained when the number of usersKis different,we only show the generalizability of DNNs to channels in a 10-user system in Tab.5.We can see that only in the test scenario withR=250 m,the policies learned by PGNs and FNNs-NoH achieve similar system performance.For other test scenarios,the availability of the policies learned by FNNs-NoH is smaller than 1.00.In the test scenarios withR=100 m and 250 m,the policies learned by PGNs and CNNs have similar system performance.For other test scenarios,the availability of the policies learned by CNNs is smaller than 1.00.Again,the policies learned by PGNs and FNNs-NoH*achieve almost the same system performance as SGD in all the test scenarios.The results indicate that the PGNs can be generalized to wireless channels,but FNNs-NoH and CNNs cannot.

Tab.5 Generalizability to channels

E.Memory and Computing Cost

Since the number of training samples has been shown in Tab.2,we only evaluate the memory and computing cost for training.In particular,we provide the minimal training time(measured by the running time on a computer with Intel®-Core™-i7-8700K CPU)and the minimal number of trainable parameters required to achieve the availability of 1.00 in all test scenarios.Again,the training and test sets for different DNNs are generated according to Tab.2.

Since only PGNs and FNNs-NoH*are applicable to different scenarios without the need of re-training,we only show their results in Tab.6.

Tab.6 Storage cost and training time

We can see that the number of trainable parameters of PGNs is very small,which is 0.24% of that of FNNs-NoH*.Besides,the training time of PGNs is 1.95%of that of FNNs-NoH*.Recall from Tab.2 that the number of training samples of PGNs is 0.83%of that of FNNs-NoH*.The results indicate that PGNs needs much lower training complexity than FNNs-NoH*to achieve the same system performance.

We also provide the inference time of the learning-based methods (PGNs and FNNs-NoH*) and the SGD method in Tab.7.As shown in the table,the inference time of the learning-based methods is identical and almost does not change withK,while the inference time of the SGD method grows withKdramatically.Specifically,the inference time of the SGD method is 3.273/0.004=818 times over that of the learning-based methods forK=5 and 21.268/0.005=4 336 times over that of the learning-based methods forK=50.

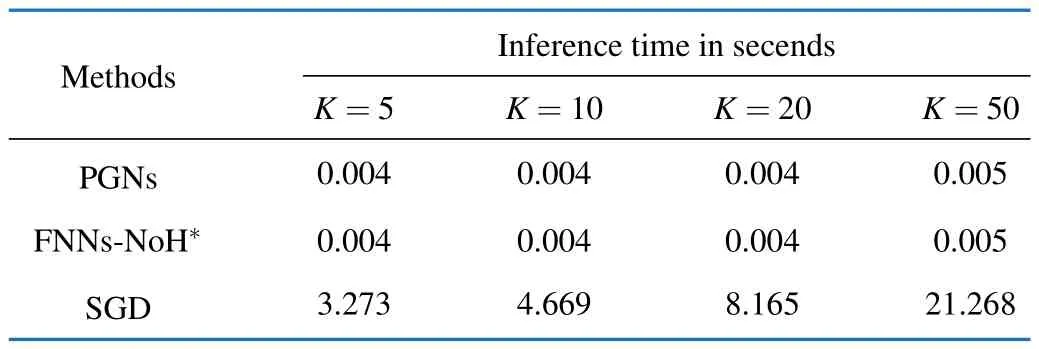
Tab.7 Inference Time

V.CONCLUSION

In this paper,we proposed a PGN for learning resource allocation policy in URLLC with low training complexity and strong generalizability.By resorting to the data pre-processing technique of ranking,the hypernetworks are very simple that can use the indices of the weights of the policy as inputs.Simulation results demonstrated that the PGNs can learn the bandwidth and power allocation policies well with ensured QoS of every user,can be well generalized to the number of users and wireless channels,and can significantly reduce the training costs compared to the existing learning-based methods.Moreover,the computing time for optimizing the resource allocation is around 0.02%for 50 users and 0.1%for five users of the time required by the SGD algorithm.