Fundamental Limitation of Semantic Communications: Neural Estimation for Rate-Distortion

Dongxu Li,Jianhao Huang,Chuan Huang,Xiaoqi Qin,Han Zhang,Ping Zhang

Abstract—This paper studies the fundamental limit of semantic communications over the discrete memoryless channel.We consider the scenario to send a semantic source consisting of an observation state and its corresponding semantic state,both of which are recovered at the receiver.To derive the performance limitation,we adopt the semantic rate-distortion function (SRDF) to study the relationship among the minimum compression rate,observation distortion,semantic distortion,and channel capacity.For the case with unknown semantic source distribution,while only a set of the source samples is available,we propose a neural-network-based method by leveraging the generative networks to learn the semantic source distribution.Furthermore,for a special case where the semantic state is a deterministic function of the observation,we design a cascade neural network to estimate the SRDF.For the case with perfectly known semantic source distribution,we propose a general Blahut-Arimoto(BA)algorithm to effectively compute the SRDF.Finally,experimental results validate our proposed algorithms for the scenarios with ideal Gaussian semantic source and some practical datasets.

Keywords—Semantic communications,semantic ratedistortion,generative network,Blahut-Arimoto algorithm

I.INTRODUCTION

With the widespread deployment of artificial intelligence in wireless communications,semantic communication is emerging as a prominent research area for future communication systems[1-4].Unlike conventional communication technologies that aim to transmit bit information from the transmitter to the receiver,semantic communication is geared towards some specific semantic tasks,e.g.,security monitoring[5]and edge inference[6].Moreover,by extracting and encoding desired information from the source data that is most relevant to the considered semantic tasks,semantic communication dramatically reduces resource consumption for communications.Therefore,semantic communication is expected to fourish in various practical scenarios,e.g.,virtual reality[7]and smart cities[8].

Semantic communication was first introduced by Shannon[9]and Weaver[10]in the 1950s,with the goal of studying the precise transmissions of semantic information.Since then,researchers have been working for several decades on how to define and model semantic information.Carnap and Bar-Hillel[11]proposed a logical probabilitybased approach to replace the statistical one in classical information theory where the amount of information is determined by its statistical rarity.Floridi[12]further proposed a semantic information theory based on logical probabilities,aiming to resolve the semantic paradox problem[13].However,the subjectivity of semantic understanding among different people poses a challenge in designing the logical probability functions that can be widely applied in practice.Moreover,many recent works focused on deep learning (DL)-based joint source-channel coding (JSCC)[14-16],i.e.,the source coding and channel coding are jointly optimized by using deep neural networks,and DL-based separate source-channel coding (SSCC)[17-19],i.e.,a deep neural network is designed to compress source symbols,followed by a classical channel coding scheme,e.g.,low-density parity check coding[20],to implement the point-to-point semantic communications.

In recent discussions within Refs.[21-22],a novel semantic source model has been introduced,defining the semantic source as two distinct components: an extrinsic observation and an intrinsic semantic state.Taking video as an example,the video signal itself serves as the extrinsic observation,while its features,which are generated based on this video for certain tasks,such as action recognition[23]and object detection[24],correspond to the intrinsic semantic state.This model employs two distortion measures,namely observation and semantic distortions,to analyze the semantic ratedistortion function[21-22],which is defined as the minimum compression rate subject to the maximum tolerable observation and semantic distortions.In this semantic source model,semantic state is generally not observable while can be inferred from the observation[21].Then,the source encoder only focuses on encoding the observation and the decoder reconstructs both the semantic state and the observation,subject to both the semantic and observation distortion constraints.Within this framework,it has been shown[22,25]that SSCC performs the same as JSCC over the infinite discrete memoryless channels.However,semantic rate-distortion function(SRDF)generally has no closed-form expression[22],and can only be effectively solved for some specifically distributed semantic sources,e.g.,Gaussian[22]and binary sources[26].Considering the high-dimensional feature of the semantic sources,e.g.,text[27],speech[28],and images[29],their distributions are general and difficult to be well modeled,making it extremely challenging to compute the corresponding SRDFs.

Despite many efforts already made in the field of semantic communications,there remains an absence of theoretical research on the fundamental analysis of SRDFs for generally distributed sources.To deal with this issue,the purpose of this paper aims to analyze the fundamental limits of the point-topoint semantic communications for general semantic sources.Specifically,inspired by the semantic source model proposed in Ref.[21],we consider a semantic source pair at the transmitter consisting of the extrinsic observation and its intrinsic semantic state.Here,only the observation data is compressed and encoded at the transmitter and then sent over a discrete memoryless channel to the receiver,where both the extrinsic observation and the semantic state are finally recovered.We aim to compute the corresponding SRDF for generally distributed semantic sources,which reveals the trade-off among the compression rate,observation distortion,semantic distortion,and channel capacity.Moreover,for the case with imperfectly known semantic source distribution,i.e.,only a certain amount of source samples are available,motivated by the neural estimation method for traditional rate-distortion functions[30],we design a neural estimator for SRDF:first,we show that SRDF can be rewritten as an inf-sup problem via its dual property;then,we leverage generative networks to solve this problem and derive the neural estimation of the SRDF(NESRD),and further show NESRD to be a strongly consistent estimator;finally,when the semantic state is a deterministic function of the observation,we design a cascade neural network framework to train the derived NESRD.For the case with perfectly known semantic source distribution,we generalize the conventional Blahut-Arimoto (BA) algorithm to numerically compute SRDF and analyze the computational complexity of this proposed algorithm.

The rest of this paper is organized as follows.Section II introduces the SSCC-based framework.Section III derives the neural estimator for SRDF under the case with imperfectly known semantic source distributions.Section IV proposes the general BA algorithm to calculate SRDF for the case with known semantic source distributions.Experimental results are presented and discussed in section V to validate the theoretical results.Finally,section VI concludes this paper.

Notation: lb(x) and ln(x) denote base-2 and natural logarithms,respectively;exstands for natural exponent;|X|denotes the size of finite alphabetX;max{x,y}is the maximum value between two real numbersxandy;(·)is the expectation for random variableXwith probability distributionPX.

II.SYSTEM MODEL

We consider a general semantic communication system,where the transmitter compresses the source data and then transmits it through a point-to-point discrete memoryless channel to the receiver for data recovery and processing specific semantic tasks.Here,a memoryless semantic source is modeled as a pair of random variables1X and S can be random vectors for the case that they are obtained from high-dimensional sources,e.g.,text[27]and images[29].(X,S) with a joint probability distribution (X,S)～P(X,S)supported on a finite product alphabetX ×S,whereXrepresents the extrinsic observation of the source,Sis the intrinsic semantic state relevant to the considered semantic task,andXandSare the alphabets ofXandS,respectively.

As shown in Fig.1,an SSCC-based semantic communication framework over the discrete memoryless channel is considered in this paper.The transmitter sends a sequence of length-nindependent and identically distributed(i.i.d.) samples of source pair (X,S),denoted as (xn,sn)=(x1,···,xn,s1,···,sn).The source encoder has access to observation sequencexn,whereasxnis related to semantic state sequencesnthrough a conditional probabilityP(Xn=xn|Sn=sn).Then,xnis compressed by the source encoder into an indexW ∈{1,···,},withRsbeing the compression rate.After that,Wis encoded by the channel encoder into a length-nchannel codeword.Then,is transmitted via the discrete memoryless channel,andis the received symbol sequence.At the receiver,the channel decoder decodesas an estimated index.Finally,the source decoder recovers the observation and semantic state sequences as=(,···,)and=(,···,),respectively.

Fig.1 Framework of SSCC scheme for semantic communications

It is noted that the asymptotic optimality of semantic communications over the infinite discrete memoryless channel can always be obtained by SSCC[22,25].Then,under the considered SSCC framework shown in Fig.1,the distortion pair(Do,Ds)is considered to be achievable if there exist separate source and channel codes such that the distortions between the transmitter and the receiver satisfyE[do(X,)]≤DoandE[(X,)]≤Ds.Moreover,we can immediately derive the following lemma to characterize the achievability of distortion pair(Do,Ds).

Lemma 2Utilizing the SSCC framework depicted in Fig.1,distortion pair(Do,Ds)is achievable if and only if

whereCis the channel capacity of the considered memoryless channel.

Remark 2It is easy to observe that Remark 1 describes the trade-off among SRDFR(Do,Ds) and distortionsDoandDs.More specifically,for any fixed semantic distortionDs,as the observation distortionDoincreases,R(Do,Ds)first decreases,and then becomes a constant equal to the conventional rate-distortion functionRs(Ds).This implies that there exists a lower bound ofDofor any fixedDs,denoted as(Ds),such thatR(Do,Ds) is degenerated toRs(Ds) whenDo≥(Ds).Similarly,there also exists a lower bound(Do) ofDssuch thatR(Do,Ds) is degenerated to the conventional rate-distortion functionRo(Do)whenDs≥(Do).Numerical results regarding SRDFR(Do,Ds)are provided in section V,which show the monotonic and convex properties ofR(Do,Ds)for some specific semantic sources.

However,there are still several challenges in effectively computing SRDFR(Do,Ds) by (1).First,it is generally not possible to derive an expression forR(Do,Ds) in closed form[22,31],and existing numerical methods for computingR(Do,Ds) are limited to some specific sources,e.g.,Gaussian[22]and binary sources[26].Second,it is much more challenging to compute SRDFR(Do,Ds)when semantic source distributionP(X,S)is not perfectly known,i.e.,only certain amount of samples of the semantic source pair (X,S) is available.To address these challenges,we propose two methods to computeR(Do,Ds)based on the assumptions of different levels of semantic source distribution information.

III.UNKNOWN SEMANTIC SOURCE DISTRIBUTIONS

This section considers the case that the exact distribution information of semantic source (X,S) is not available,while its realizations are obtained from some large and highdimensional datasets.First,we rewriteR(Do,Ds) in (1) as an inf-sup form.Then,we propose a neural-network-based method to computeR(Do,Ds)and design a cascade neural network framework for a special case ofR(Do,Ds) whenSis a deterministic function ofX.

A.Reformulation of R(Do,Ds)

Proposition 1The semantic rate function defined in(3)can be equivalently computed as

ProofPlease see Appendix B).

Proposition 2R(Do,Ds) given in (1) can be equivalently computed as

and it has the same optimal solutions as problem(1).

ProofPlease see Appendix C).

Together with Propositions 1 and 2,SRDFR(Do,Ds) can be equivalently written as the following inf-sup problem.

To solve this inf-sup problem,one straightforward idea is to first solve the inner supremum of(7),and then use the gradient descent method to optimize design variableQ.As proved in Appendix B),objective function in (7) is strictly concave with respect toα1andα2,and thus possesses a unique solution to its inner supremum satisfying.

where(8)and(9)are obtained by checking the first-order condition of the objective function in (7).However,it is difficult to get explicit expressions forα1andα2from (8) and(9),making the computation of SRDFR(Do,Ds)challenging.Therefore,we present the following proposition to address this challenge.

Proposition 3For any fixedα1andα2,α1,α2≤0,considering

B.Neural-Network-Based Approach

This subsection proposes a neural-network-based approach to solve problem (10),and then derives the NESRD forR(,).Specifically,to tackle the challenges discussed in Remark 3,we first design a generative neural network that takes a simple distribution,e.g.,Gaussian distribution,as input,and aims to approximate distributionas closely as possible.Then,parameters of the generative network are trained via gradient descent methods to minimize the objective function in (10).Finally,SRDFR(,) given in (11)is estimated by samples of(X,S)and the well-trained generative network.

First,we introduce a latent variableZfollowing distributionPZover alphabetZand then define a generative neural network fromZto×asH(z,θ)=[H(1)(z,θ),H(2)(z,θ)]T,withH(1)(z,θ) andH(2)(z,θ) being realizations of reconstructed sourcesand,respectively,andθ ∈Θbeing the parameter to be optimized.After that,we replaceQin(5)with generative networkH(Z,θ),which allows us to formulate problem(10)in terms of parameterθ,i.e.,problem(10)is transformed as

Then,we propose an iterative training algorithm to minimize problem (12) by optimizing parameterθof the generative networkH(Z,θ).We select i.i.d.samplesx1,···,fromPX,i.i.d.samples,···,from the conditional distributionfor each sample,n1=1,···,N1,and i.i.d.samplesz1,···,zMfrom distributionPZ,withN1,N2,andMbeing the number of observation samples,semantic state samples,and samples of latent variableZ,respectively.Then,by approximating expectations in (12) with empirical averages over these samples of(X,S)andZ,(12)is rewritten as

Here,the objective function in(13)is defined as the loss functionLθ(α1,α2)for training generative networkH(Z,θ).Besides,in order to ensure that the gradient of the loss function∇θLθexists,distortion measuresdoanddsmust be differentiable.After that,we proceed to update parameterθby leveraging the gradient ∇θLθand employing the backpropagation algorithm[35].

By utilizing the well-trained generative networkH(Z,θ⋆)withθ⋆being the trained parameters,we derive the NESRD for semantic source (X,S),which is summarized in the following proposition.

Proposition 4For any fixedα1andα2,α1,α2≤0,NESRD for semantic source(X,S)is given as

ProofIt is easy to see that (14)-(16) are obtained by replacingin (8) and (9) withH(Z,θ⋆),approximating expectations in(8)and(9)with empirical averages over training samples given in (13),and replacing ΛQ⋆(α1,α2) in (11)with-Lθ⋆(α1,α2)defined in(13).

In conclusion,we summarize the neural-network-based approach for NESRD in Algorithm 1.

Remark 4Although NESRD has been shown in Corollary 3.1 to be a strongly consistent estimator of SRDF,it is

essential to note that its estimation inaccuracy is sensitivity to the number of samples.More specifically,it has been proved in Refs.[30]and [36]that NESRD(,) cannot be larger thanO(lbN1N2)withN1N2being the number of semantic source samples in(14).

Remark 5It is easy to see that Algorithm 1 can be utilized to estimate SRDFs for the case with perfectly known semantic source distributions.In such cases,the required i.i.d.semantic source samples in(13)can be directly generated from the known source distributionP(X,S).Then,the corresponding NESRD can be obtained by Algorithm 1 accordingly.

C.A Special Case for NESRD

In this subsection,we mainly analyze a special case for SRDFR(Do,Ds),where the intrinsic semantic stateSis a deterministic function of the extrinsic observationX,i.e.,the semantic source(X,S)is obtained from labeled datasets,e.g.,MNIST,SVHN,and CIFAR-10 datasets.In such datasets,the raw images are samples of extrinsic observationX,while their corresponding labels can be regarded as samples of intrinsic semantic stateS.For the ease of analysis,it followsS=h(X),and accordingly,semantic distortion measure(x,) in (1)can be simplified as

Moreover,we further design a cascade neural network framework to estimate SRDF for the case withS=h(X),which is depicted in Fig.2.Under this framework,generative networkH(Z,θ) is composed of a generatorG(Z,θ1) and a classifierF(,θ2),θ=[θ1,θ2]T,with the generator producing samples of reconstructed observation,and the classifier generating samples of reconstructed semantic state.Besides,sinceSis a function ofX,we consider the case thatcan also be regarded as a function ofso that its distributioncan be directly estimated by.Therefore,the generator is connected with the classifier in series,and the generative networkH(Z,θ)defined in(12)is now equivalent to

Fig.2 Training diagram for NESRD with S=h(X)

Moreover,together with (18) and (19),the loss function in (13)for training parametersθcan be simplified as

Here,(x1,s1),···,(xN1,sN1)are i.i.d.sample pairs from the labeled dataset.First,generatorG(Z,θ1)and classifierF(,θ2)are both pre-trained by the labeled dataset.Then,similar to the training procedure in Algorithm 1,we iteratively update parametersθby utilizing the gradient of the loss function∇θ(α1,α2) and the backpropagation method[35].Finally,as the training algorithm converges,,,and(,)are calculated by (14)-(16),with(·),H(·),andLθ(·) in(14)-(16) being replaced with (18),(19),and (20),respectively.In conclusion,we summarize the training algorithm for estimating the SRDF for labeled datasets in Algorithm 2.

IV.PERFECTLY KNOWN SEMANTIC SOURCE DISTRIBUTIONS

This section considers the case that the distribution of semantic source pair (X,S) is completely known and has a discrete form2When semantic source distribution P(X,S) is not discrete,we can approximate it with a discrete distribution by discretizing the possible values of(X,S)into a finite number of points and estimating their corresponding probability mass functions via the known distribution P(X,S).,and we generalize the conventional BA algorithm[40-41]to numerically compute SDRFR(Do,Ds).Besides,we analyze the computational complexity of the proposed general BA algorithm.

A.General BA Algorithm

To derive the general BA algorithm,we first show that computingR(Do,Ds)in(1)is equivalent to solving the following double minimum problem.

Lemma 3For any fixedλ1≤0 andλ2≤0,there existandsatisfying

respectively,where (23) and (24) are the generalizations of those iteration steps in the conventional BA algorithm[31].Moreover,as the iteration indexkgoes to infinity,we have

respectively.Besides,the convergence in(25)is obtained similar to that of the conventional BA algorithm[31].

B.Computational Complexity

It is easy to see that|X|grows exponentially with respect to the dimension ofX,leading to an exponential growth in the computational complexity of the proposed general BA algorithm.This drawback also applies toS.Moreover,semantic source pair (X,S) is typically derived from large datasets in practical applications and exhibits high-dimensional characteristics,rendering the general BA algorithm inefficient in such cases.

V.NUMERCIAL AND SIMULATION RESULTS

In this section,we present some experimental and simulation results to validate the proposed NESRD for various typical semantic sources.First,we examine the case whenXandSare jointly Gaussian,and compare the proposed neural-network-based approach with the proposed general BA algorithm and the semi-definite programming(SDP)method[22].Then,we calculate the NESRD for some classical image datasets,e.g.,MNIST and SVHN datasets,and compare it with the hyperprior-based compression method[42],which adopted as the benchmark for the DNN-based image compression schemes.

A.Joint Gaussian Source

1) Datasets:In this subsection,extrinsic observationXfollows a multivariate Gaussian distributionN(0,KX),and intrinsic semantic stateSsatisfiesS=HX+W,whereHis a constant matrix andWis also a Gaussian random vector followingN(0,KW).KX,H,andKWare set as[21]

To leverage Algorithm 1 for NESRD of the joint Gaussian source (X,S),we generate a sample set as follows: First,we independently obtainN1=50 000 samples ofXfollowing the distributionN(0,KX).Then,for each sample,n1=1,···,50 000,we selectN2=1 000 samples ofSwhich are drawn i.i.d.from the conditional distributionP(S|X=)～N().

3) Experiments:Fig.3 plots the surface and contour of NESRD(Do,Ds) for the joint Gaussian source given in(26).It is easy to see that,with fixedDs,(Do,Ds)exhibits a diminishing trend asDoincreases.However,the decreasing rate gradually attenuates with the augmentation ofDo.Then,whenDoremains fixed,for smaller values ofDo,(Do,Ds)is insensitive to variations inDs;whereas for larger values ofDo,(Do,Ds)experiences a substantial reduction asDsincreases.For example,whenDois around 1,changes inDsscarcely impact(Do,Ds).In contrast,whenDoequals 15,asDsincrements,(Do,Ds) undergoes a notable decrease from around 2 to 0.

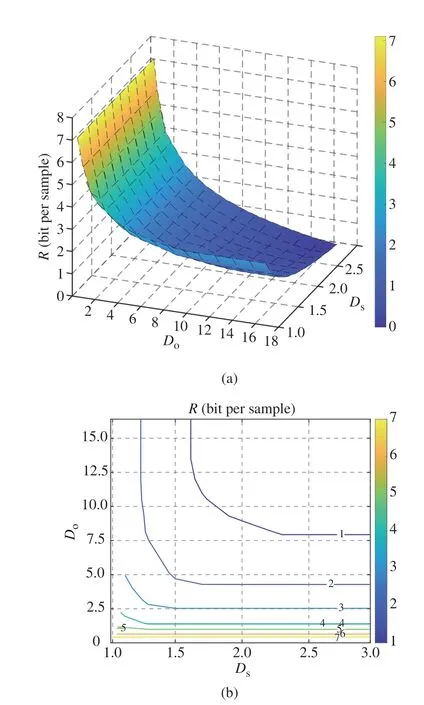
Fig.3 NESRD(Do,Ds) for joint Gaussian source by Algorithm 1: (a)surface of(Do,Ds);(b)contour of (Do,Ds)

Fig.4 compares the performance of NESRD(Do,Ds),SDP-computedR(Do,Ds)[22],andR(Do,Ds)computed by the proposed general BA algorithm in Algorithm 3 for the joint Gaussian source.It is noted that by directly leveraging the distribution of the joint Gaussian source (X,S),the SDP method is able to numerically compute the corresponding SRDFR(Do,Ds) in a stable and efficient manner[22].Moreover,it shows that(Do,Ds)is remarkably close to the SDPcomputedR(Do,Ds)for any distortion couple(Do,Ds),which reveals that the proposed NESRD is a good estimator for the SRDF in this example.However,R(Do,Ds)computed by the general BA algorithm exhibits slight deviations from the other two methods at the low rate region (R≤4 bits per sample).These deviations are potentially attributed to the errors introduced during the discretization of the joint Gaussian source distribution in the general BA algorithm.

Fig.4 Performance comparisons among NESRD,SDP method[22],and proposed general BA algorithm for joint Gaussian semantic source: (a)(Do,Ds) vs. R(Do,Ds) for fixed Do;(b) (Do,Ds) vs. R(Do,Ds) for fixed Ds

B.Image Datasets

1)Datasets:In our experiment,we calculate the NESRD for MNIST and SVHN datasets by utilizing Algorithm 2.

2) Training Settings:We consider that each image in the labeled dataset is a sample from extrinsic observationPX,and its label is a sample from the intrinsic semantic distributionPS.Besides,we utilize one-hot encoding to represent the labels.Therefore,the semantic samplesis a one-hot vector with 10 dimensions.The distribution of the latent variableZis set to bePZ=N(0,I100)with 100 being the dimension of the latent space.The generatorGis parameterized by a convolutional neural network (CNN) with 3 convolutional layers,3 pooling layers,and 2 fully connected layers,where the output of the generatorGis used to represent.The classifierFis also parameterized by a CNN with 2 convolutional layers,2 pooling layers,and 2 fully connected layers.Besides,the classifierFoutputs a probability distribution over 10 classes,which is used to represent a sample of.Then,the learning rates of generatorGand classifierFare both set as 1×10-4and the training epoch is set as 50.Besides,we setN1=40 000 for the considered two datasets.Moreover,we adopt the squared-error distortion measures for the extrinsic observation,i.e.,.As for the intrinsic semantic state,its distortion measureds(s,) is defined to be the cross entropy betweensand,i.e.[43].

3) Experiments:For MNIST dataset,we draw the surface of the corresponding NESRD(Do,Ds),and also plot(Do,Ds) as a function ofDofor fixed values ofDsin Fig.5.Specifically,Fig.5(a) illustrates the overall decreasing trend of(Do,Ds) with respect toDoandDs.Moreover,as depicted in Fig.5(b),when extrinsic observation distortionDois less than 25,semantic distortionDshas only a little effect on(Do,Ds),which indicates that the recovered observation statealmost contains the entire semantic informationS;Conversely,forDo＞25,the impact ofDson(Do,Ds) gradually intensifies and the smallerDs,the larger(Do,Ds).Additionally,forDs=0.01 andDo＞47,(Do,Ds) decreases to a constant,which is approximately equal to lb10.This aligns with the case that only the semantic information,i.e.,labels of MNIST images,is nearly losslessly compressed,since the conventional rate-distortion functionRs(Ds)defined in Remark 1 satisfiesRs(0)=lb10.

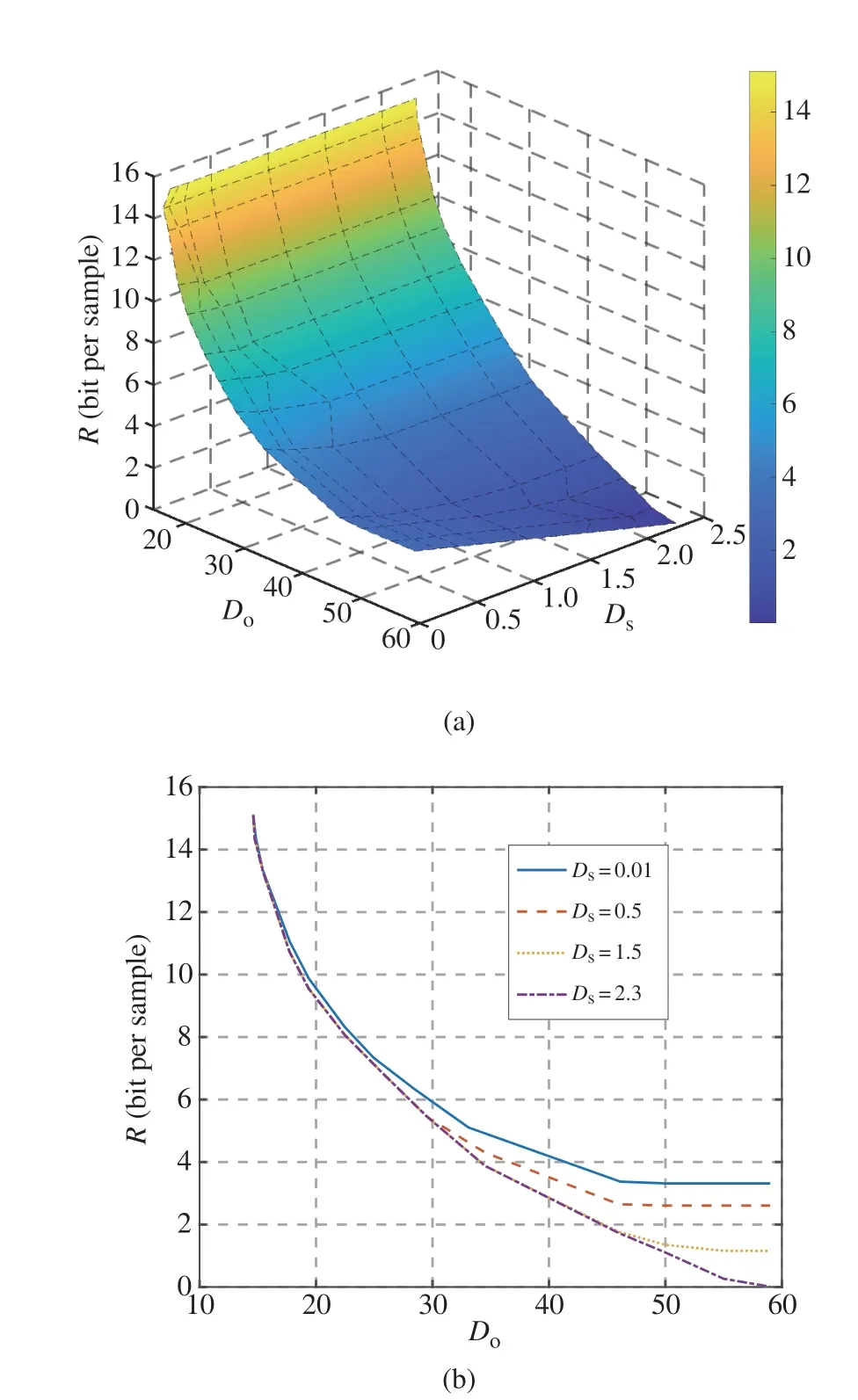
Fig.5 NESRD(Do,Ds)for MNIST dataset: (a)surface of(Do,Ds);(b)(Do,Ds)vs. Do

Then,for MNIST dataset,as shown in Fig.6,we compare NESRD(Do,Ds) with the hyperprior-based compression method[42]by using the same values ofDoandDs.It is easy to see that(Do,Ds)is significantly smaller than the compression rate of the hyperprior-based compression method.This indicates that there is significant potential for enhancing the performance of current DNN-based compression algorithms when applied to the compression of a specific dataset.For example,most existing compression algorithms typically compress one image at a time.However,jointly compressing multiple images from the same dataset has the potential to further boost the compression performance.

Fig.6 Performance comparisons between NESRD and the hyperprior-based compression method[42]for MNIST dataset

Moreover,we further show the performance of NESRD for SVHN dataset,which is depicted in Fig.7 and 8.Specifically,similar to Fig.5(a),Fig.7 depicts the overall decreasing trend of(Do,Ds) with respect toDoandDsfor SVHN dataset.Notably,the range ofDofor SVHN dataset is quite larger than that of the MNIST dataset,due to the fact that SVHN images are in color,whereas MNIST images are grayscale.Then,in Fig.8(a),when extrinsic distortionDois small,semantic distortionDshas only a little effect on(Do,Ds);asDobecomes larger,the impact ofDson(Do,Ds)gradually intensifies,which performs similar to that of MNIST dataset shown in Fig.5(b).Moreover,we also plot(Do,Ds)as a function ofDsfor fixed values ofDoin Fig.8(b).It is easy to see that variations inDscan result in changes in(Do,Ds)up to approximately lb10 bits,which aligns with the results of(28)sinceRs(Ds)satisfiesRs(0)=lb10.Finally,we also conduct a comparison between NESRD(Do,Ds)and the hyperpriorbased compression method[42]for the SVHN dataset,which is shown in Fig.9.Similar to the findings observed in the MNIST dataset (as depicted in Fig.6),our comparisons reveal that(Do,Ds) for SVHN is also notably smaller than the compression rate achieved by the hyperprior-based compression method.

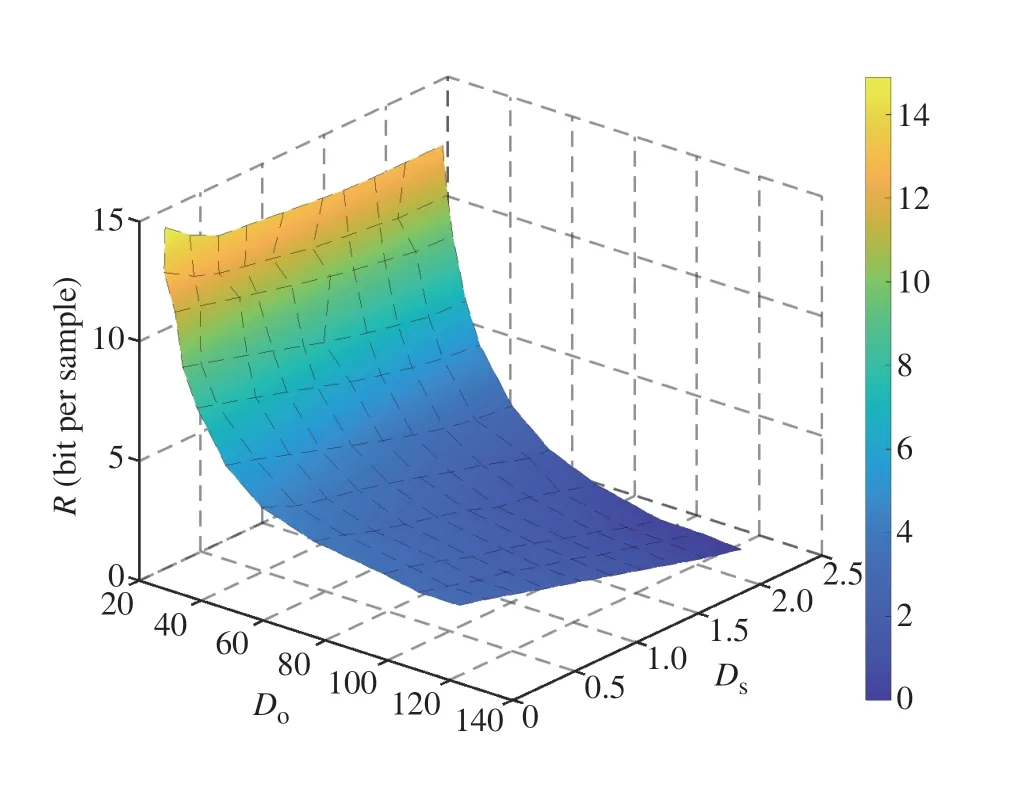
Fig.7 Surface of (Do,Ds)for SVHN dataset

Fig.8 NESRD(Do,Ds)for SVHN dataset: (a)(Do,Ds)vs. Do;(b)(Do,Ds)vs. Ds

Fig.9 Performance comparisons between NESRD and the hyperprior-based compression method[42]for SVHN dataset

VI.CONCLUSION

This paper proposed an SSCC-based framework for pointto-point semantic communications,which explored SRDF to study the trade-off among the minimum compression rate,observation distortion,semantic distortion,and channel capacity for generally distributed semantic sources.In addressing scenarios with imperfectly known semantic source distribution,we employed a generative network to propose NESRD,a strongly consistent neural estimator of SRDF.This approach enhances the understanding of SRDF in cases where only partial knowledge of semantic source distribution is available.Furthermore,we proposed a generalized BA algorithm devised to solve SRDF for instances with perfectly known semantic source distributions.The computational complexity of this algorithm was thoroughly discussed,providing insights into its feasibility and efficiency.To validate the reliability of our theoretical analysis,experimental results were presented for a joint Gaussian source and various typical image datasets,showcasing the applicability and robustness of our proposed framework.

APPENDIX

A)Proof of Remark 1

First,SRDFR(Do,Ds)is bounded as[26]

B)Proof of Proposition 1

First,we present a lemma about ΛQ(α1,α2) to reveal its strictly convex property.

Lemma 4ΛQ(α1,α2)is strictly convex over the feasible region{(α1,α2):α1≤0,α2≤0}.

ProofFor simplicity,we define

The above second-order partial derivatives are difficult to be directly analyzed.For simplicity,we consider a probability measure(x)on×defined as

Then,combining(34)with(31)-(33),the second-order partial derivatives with respective to(α1,α2)are simplified as

where (38) is derived by Cauchy-Schwarz inequality.Therefore,(α1,α2)is a convex function with respect to(α1,α2).Since ΛQ(α1,α2)=EPX[(α1,α2)],it can be easily derived that ΛQ(α1,α2)is also convex.

Next,we will prove that ΛQ(α1,α2)is actually strictly convex.From(29),it is easy to verify that

It is easy to verify that the first marginal distributionWXofWisPX,Then,we have

By substitutingxwithXand taking expectations with respect toPXon both sides,we obtain

C)Proof of Proposition 2

D)Proof of Proposition 3

where (62) holds since (α1,α2) is the stationary point of the objective function in(61)given in(8)and(9).Finally,Combining(60)with(62),we have

Together with (42),(11) is obtained and we have completed this proof.