A Model-Driven Approach to Enhance Faster-than-Nyquist Signaling over Nonlinear Channels

Tongzhou Yu,Baoming Bai,Ruimin Yuan,Chao Chen

Abstract—In order to increase the capacity of future satellite communication systems,faster-than-Nyquist(FTN) signaling is increasingly considered.Existing methods for compensating for the high power amplifier(HPA) nonlinearity require perfect knowledge of the HPA model.To address this issue,we analyze the FTN symbol distribution and propose a complex-valued deep neural network (CVDNN) aided compensation scheme for the HPA nonlinearity,which does not require perfect knowledge of the HPA model and can learn the HPA nonlinearity during the training process.A model-driven network for nonlinearity compensation is proposed to further enhance the performance.Furthermore,two training sets based on the FTN symbol distribution are designed for training the network.Extensive simulations show that the Gaussian distribution is a good approximation of the FTN symbol distribution.The proposed model-driven network trained by employing a Gaussian distribution to approximate an FTN signaling can achieve a performance gain of 0.5 dB compared with existing methods without HPA’s parameters at the receiver.The proposed neural network is also applicable for non-linear compensation in other systems,including orthogonal frequency-division multiplexing(OFDM).

Keywords—Faster-than-Nyquist signaling,high power amplifier,nonlinear compensation,complex-valued neural network

I.INTRODUCTION

Future wireless communication systems,such as beyond 5G and 6G,have been getting a larger demand for higher transmission rates and spectral efficiency[1],which require integration of non-terrestrial networks.To this end,faster-than-Nyquist (FTN) signaling,a non-orthogonal waveform technology,has been considered as a promising candidate to improve the spectrum efficiency without the requirement of additional bandwidth or antennas[2].FTN signaling was first proposed by Mazo in 1975[3],which breaks the orthogonality between transmitted symbols by compressing the symbol period to effectively improve the spectral efficiency.More importantly,FTN signaling is able to achieve the ultimate capacity of the additive white Gaussian noise (AWGN) waveform channel with the signal power spectral density(PSD)[4].As a result,the option of using faster-than-Nyquist signaling in digital video broadcasting-satellite-second generation extensions(DVB-S2X) satellite application systems have been actively considered[2,5-6].

One challenge in FTN signaling is the presence of intersymbol interference (ISI),which occurs when symbols overlap with each other.In the downlink of satellite communication systems such as DVB-S2X,higher-order constellations are adopted for achieving higher spectral efficiency[7].This can make it more difficult and accurate to detect the transmitted signal in the FTN transmission system.The Bahl,Cocke,Jelinek,and Raviv (BCJR) algorithm[8]is an efficient maximum a posteriori probability (MAP) algorithm whose complexity is exponential in the number of ISI taps.A common approach for reduced-complexity MAP detection is a simplification of trellis search within the BCJR algorithm[9-10].With the factor graph representation of ISI channels,a sum product algorithm and its variants[11]are considered,which have a computational complexity linear in the number of ISI taps compared to the exponential complexity of the BCJR algorithm.Another challenge is nonlinear distortion in the transmit signal caused by the satellite’s high power amplifier (HPA).HPA often operates near saturation to maximize the power efficiency and introduces amplitude and phase distortion[12].ISI will be further increased when the FTN signaling passes through the HPA compared to the Nyquist signaling.Hence one of the key issues is designing FTN signaling with low peak-to-average power ratio (PAPR),which helps minimize the nonlinear distortion[13-14].

Fewer works available have considered HPA nonlinearity compensation for FTN transmission.The Forney observation model is applied to nonlinear channel through a linearized Volterra series approach[7].For better performance,the estimation of the nonlinear channel is required.A synchroization scheme for FTN signaling is proposed in a satellite context[15].The approach is based on a Volterra decomposition of the received signal to accommodate both linearized and non-linearized amplifiers present in the satellite payload.And channel estimation is employed to address time offset issues in the proposed schemes.The authors propose a post-distortion detection scheme for memoryless power amplifiers with a perfect knowledge of the HPA’s input-output characteristics[12].

Motivated by the above observations,in this paper we propose a model-driven compensation scheme for FTN transmission without HPA’s parameters at the receiver.We analyze the FTN symbol distribution,and use the Kullback-Leibler(KL)divergence to measure the difference between the symbol distribution and Gaussian distribution.A complex-valued deep neural network (CVDNN) aided compensation scheme is then proposed to compensate for the nonlinear distortion of the HPA with unknown parameters of HPA.A model-driven CVDNN network for compensation is designed for a better performance.Furthermore,we train the models by assuming a Gaussian distribution to approximate the FTN signaling.

The rest of this paper is organized as follows.In section II we introduce a coded FTN system with the high power amplifier.FTN signaling generation and power amplifier model are discussed in detail.In section III,we first derive the expression of FTN symbol and use a method to measure the difference between FTN symbol distribution and Gaussian distribution.Then,we propose a CVDNN-based compensation scheme.For better performance,by unfolding iterative process,we propose a model-driven CVDNN network for compensation.The training process and training data are also discussed in detail.In section IV,we evaluate the performance of the proposed scheme by simulation and show that it can achieve a better performance than the existing scheme.

II.SYSTEM MODEL

A.FTN Signaling Generation

Consider the downlink transmission of a satellite communication system as shown in Fig.1.Assume that the sequenceuof information bits with average powerEbis encoded into a codewordcby a forward error correction (FEC) encoder.The code bits are then interleaved and mapped into modulated symbol sequencex={xn}with thenth symbolxntaking on values in alphabetX.The baseband FTN signals(t)is generated by upsampling the symbol sequencexof lengthNand pulse shaping[3]with the following expression.

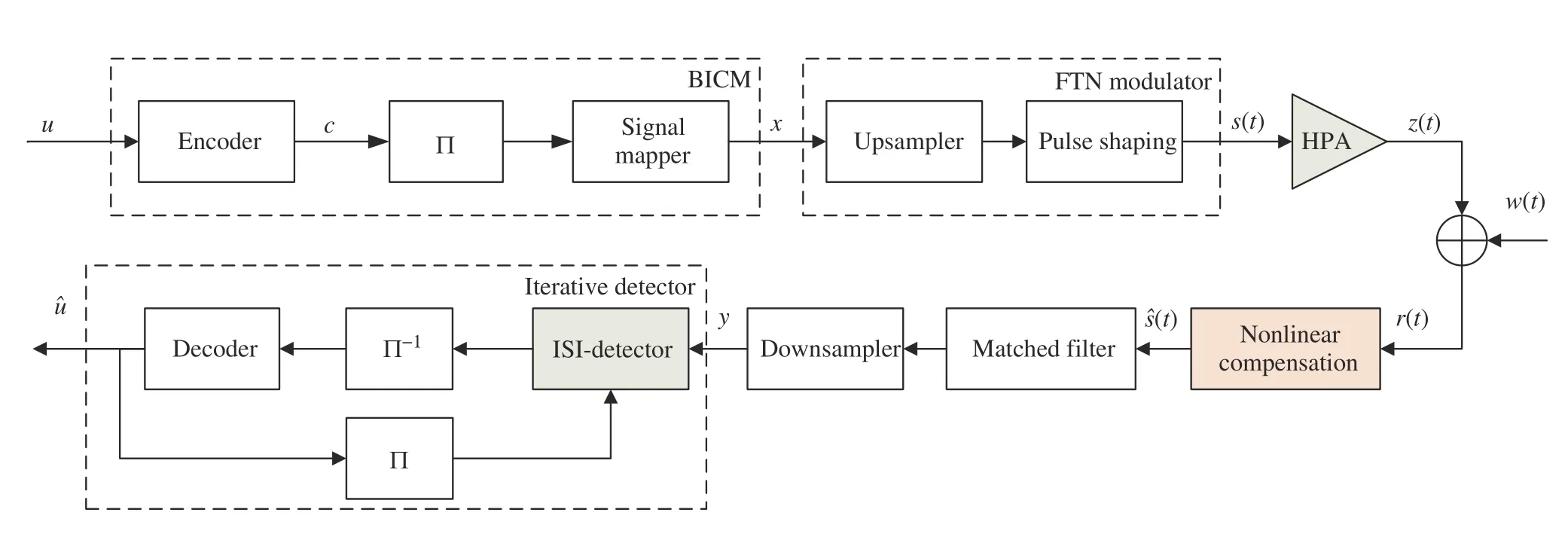
Fig.1 System model of the proposed coded FTN with HPA(Π denotes the interleaving)

wheretis time,p(t) is assumed be theT-orthogonal root raised cosine(RRC)pulse with a roll-off factorβ,andτ ＜1 is the FTN time-compression factor.Note that the symbol periodτTof the FTN signaling is shorter than that of the Nyquist signaling.Whenτ=1,the FTN signaling is degraded to the Nyquist signaling.

B.Power Amplifier Model

Before transmission,the FTN signals(t)is amplified by an HPA.In order to obtain the efficient power amplification,the HPA usually operates in the saturation region and the output signal is nonlinearly distorted.The general HPA model for describing the nonlinear distortion is the well known Volterra series[16].A simplified model,commonly used to describe an HPA is the following memoryless polynomial model[17].

whereα2d-1is the complex coefficient of the(2d-1)th order nonlinearity,which contains the amplitude and phase distortion effects.Thes(t)andz(t)are the input and output signals of the HPA,respectively.For the model of(2),D=2 is usually assumed[12],which takes into account the nonlinear infuence each timeslot,and ignores the inter-modulation component.It has been widely used because its fitting accuracy for nonlinear effects and memory effects is moderate.

Suppose thatz(t) is transmitted over the AWGN channel.The receiver gets the signalr(t)=z(t)+w(t),wherew(t)represents a circularly-symmetric Gaussian random process with a one-sided PSD ofN0.At the receiver side,the nonlinear detector is performed uponr(t)to compensate for the nonlinear distortion and recover the original signal,resulting in(t).We consider(t) as a biased estimate ofs(t),and the bias is denoted bywbias(t).As a result,the output of the nonlinear detector is

Moreover,to simplify the analysis,the detector noisewbias(t)is assumed to be a complex circularly-symmetric Gaussian noise with two-sided PSD ofwhich is proportional toN0and independent of FTN signals(t).

C.FTN Signal Detection

After nonlinear compensation,the signal(t)is first passed through a matched filter with impulse responsep*(t) and is then sampled for detection at the rate of 1/(τT).We obtain the discrete-time signal sequence as

LetLrepresent the number of channel taps with significant power on one side.The rest ISI terms with insignificant energy are therefore neglected and then set to zero in the following analysis,i.e.,gl=0 for|l|＞L.The termηnin(4)and(6)represents the colored noise due to a matched filter,whose autocorrelation function satisfies,where (·)Hdenotes the conjugate transpose andGis a Toeplitz matrix of full rank[18]given by

We can express(4)in matrix form asy=Gx+η.An iterative soft information detection between ISI detector and FEC decoder is performed to recover the transmitted symbols based on the sequencey.In this work,we will utilize the sum product algorithm(SPA)for ISI detection[11].Such detector has a relatively low complexity and can achieve a near-optimal performance in high-order constellations.

Note that the nonlinear detector performs symbol sequence detection prior to the ISI detector.We are considering implementing nonlinear compensation at the receiving end,avoiding the use of digital pre-distortion(DPD)at the transmitter to mitigate potential declines in power efficiency.It is a challenging task to compensate for nonlinear distortion,which will be discussed in the next section.

III.NONLINEAR DISTORTION COMPENSATION

A.FTN Symbol Distribution

Due to the receiver’s limited knowledge of the accurate nonlinear input-output characteristics of the HPA,we consider AI-aided nonlinear compensation.We first need to know the distribution of FTN symbol to train the nonlinear compensation module better.For quadrature amplitude modulation(QAM),the real and imaginary parts are independent and identically distributed.It could be shown that the real and imaginary parts of FTN symbol are also independent and identically by(1).The distribution of real part of FTN symbol is considered in the following discussion.Without loss of generality,the real part of FTN signal is sampled at the time instantt=0,and we obtain the following expression.

where ℜ{·}denotes the real part of a complex value.Withxl ∈X ⊂C,ℜ{xl} corresponds to thelth pulse amplitude modulation (PAM) symbol.The expressionp(-lτT) varies withlslowly and may be approximated as a constant ifτorβis sufficiently small.In this case,ℜ{s0}is a linear combination of independent and identically distributed (i.i.d.) random variables.According to the central limit theorem,ℜ{s0}can approximate a Gaussian random variable.The imaginary part of FTN symbol ℑ{s0}can be analyzed in the same way.Therefore,the FTN symbols0is a complex Gaussian-like random variable.

We use KL divergence as a metric to measure the difference between the distributionpof ℜ{s0} and a standard normal distributionq,which is defined as follows.

The detailed results are discussed in section IV for ensuring the accuracy of the approximation.

B.CVDNN-Aided Nonlinear Detection Scheme

By(2),we have the following expression for brevity.

For memoryless HPA,Hin(10)is a diagonal matrix.A more specific form is given below.

It is obvious thathn=∑d α2d-1|sn|2(d-1)depends on instantaneous power ofsnand the HPA’s parameters{α1,α3,···,α2D-1}.Perfect knowledge of the above parameters is required for the nonlinear detection.As is shown in Algorithm 1,the NLD algorithm is based on perfect knowledge of the HPA model[12].However,in practice,the HPA’s parameters{α1,α3,···,α2D-1} are unknown and the instantaneous power ofsnis not available.For this issue,we propose a complex-valued deep neural network aided nonlinear detection scheme and combine estimation and detection together for a better performance.CVDNN is a neural network with complex-valued weights and activations.It has been shown that CVDNN can achieve better performance than real-valued deep neural network in handling the natural complex-valued and signals[19].We use CVDNN to estimate above parameters and instantaneous power{|sn|2,|sn|4,···,|sn|2D-2}instead of the commonly used real number neural network.

As is shown in Fig.2,the CVDNN in this work is a fully connected neural network with 2 hidden layers.The first layer extracts the features of the input signal,and the second hidden layer combines the features and further extracts the features of the input signal.The last output layer predictshnin this study.The training and parameter optimization will be discussed in section III.As is shown in Algorithm 2,CVDNN works as a part of the nonlinear detection.The CVDNN performs different functions during the training and testing phase.

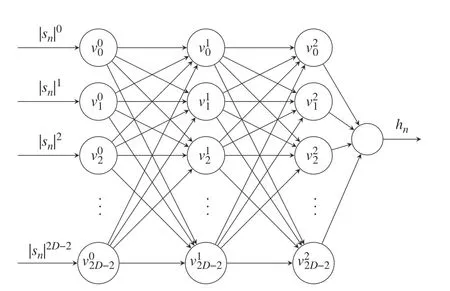
Fig.2 The structure of CVDNN,represents a temporary variable within the hidden layers

During the training phase,the CVDNN is trained to estimate the unknown key parameters of HPA model offine.Once the training is done,the estimated parameters are fixed.The network can perform the nonlinear detection directly to compensate for the nonlinear distortion.Just one tiny CVDNN is needed to implement the nonlinear detection for all the received signals for memoryless HPA.

C.Model-Driven CVDNN Network for Nonlinearity Compensation

It is clear that the CVDNN-aided nonlinear detection is an iterative process and adopts the same CVDNN for each iteration.By the use of deep unfolding first introduced in Ref.[20],the iterative algorithm 2 can be converted to a deep neural network,which is called model-driven CVDNN network.Fig.3 illustrates that the model-driven (MD) network.Networks CVDNN1(·),CVDNN2(·),···,CVDNNK(·)have the same connection but different weights and share a common connectivity pattern as shown in Fig.2.It is important th[at we map the input]signalsnin a higher dimensional spaceto deal with the nonlinear distortion.In this way,the network can be controlled and fine-tuned in a more precise manner for a better performance.

Fig.3 The model-driven CVDNN network for nonlinear compensation

This adjustment is based on the feedback received from training samples,enabling the network to minimize the discrepancy between its actual output and the expected output.In the case of the large network depicted in Fig.3,each small module has its own relative optimal weights to better perform its respective subtask.Its connectivity is designed according to the expression ofhn.This connectivity ensures that the model maintains interpretability while achieving improved performance with less data.

D.Training and Parameter Optimization

Sampled FTN symbols have a very large alphabet size|X|2L-1and could be considered approximately continuous ifτis small enough.For example,the alphabet size is 165=1 048 576 forL=3 and|X|=16.Our approach focuses on compensating for the HPA effect on the FTN symbols,which will output hard decision values on the FTN symbols instead of providing the log likelihood ratio values for each FTN symbol.Therefore,we optimize the parametrization towards a minimum mean-square error(MMSE)between HPA inputssand desired outputsas follows.

where complex-valuedsnandare thenth element ofsand,respectively.MMSE here is used for loss function with more focus on the amplitude distortion.

When training complex-valued networks,the gradient computation follows a similar process to real-valued networks.However,the loss function(12)is non-holonomic and may not have complex differentiability.Wirtinger developed a framework that simplifies the process of the derivative of complex valued functions with respect to both holomorphic and nonholomorphic functions[21].By doing this,the derivatives to the loss can be computed in the complex domain.An identity function[19]is used as activation function.We use the Adam algorithm[22],a stochastic gradient descent method,to minimize the loss function.All weights are initialized with a Xavier Gaussian distribution[23].

These are two different ways to generate training data.The first one is more accurate on a certain FTN system,while the second one is more general.By the analysis in section III,we can obtain that it is more robust toτandβ.

1.Generate FTN symbols using the given parametersτ,β,and channel outputraccording to (11).Thenris fed into the network to recover the FTN symbols.Finally,the parametrization on training is performed.

2.Sample a complex Gaussian distribution i.i.d.as a good approximation of FTN signaling and optimize the network parameters.

IV.SIMULATION RESULTS AND ANALYSIS

Without loss of generality,we choose RRC with a rolloff factorβ=0.3 as the shaping pulse.Setτ=0.8 and the length of the truncated ISIL=5.Meanwhile,5G new radio (NR) low density parity check (LDPC) codes are chosen as the FEC code,where the length of the sequence of information bits in one block is set 1 024 and the code rate isRc=1/2 andRc=2/3.16-QAM mapping is used in this study because the nonlinearity of HPA is more severe for higher order modulations.Furthermore,the HPA parameters,as stated in Ref.[24],are given byα1=0.979 8-0.288 7j andα3=-0.290 1+0.435 0j.We do not consider using power backoff to reduce the nonlinear distortion as it is a negative measure.The HPA input back-off(IBO)is set to 0 dB.We consider worse-case scenario,where the HPA is driven to its saturation point.The maximum iteration number is set toK=3.

First,we analyze the distribution of the FTN symbol and compare it to the standard Gaussian distribution.The KL divergence between these two distributions is shown in Tab.1.To perform this analysis,we sample the standard Gaussian distribution from-10 to 10 with a step of 0.01.The results indicate that as the roll-off factorβand the time-compression factorτdecrease,the KL divergence tends to become smaller,possibly even approaching zero.This suggests that the Gaussian distribution can effectively approximate the FTN symbol distribution.To further illustrate this,Fig.4 provides a visualization of the two distributions at specific values ofβandτ.These results give us a better understanding of the FTN symbol distribution and guide us to use the complex Gaussian distribution as training data set for the neural network.

Tab.1 KL divergence DKL (bit)between the FTN symbol distribution and the Gaussian distribution

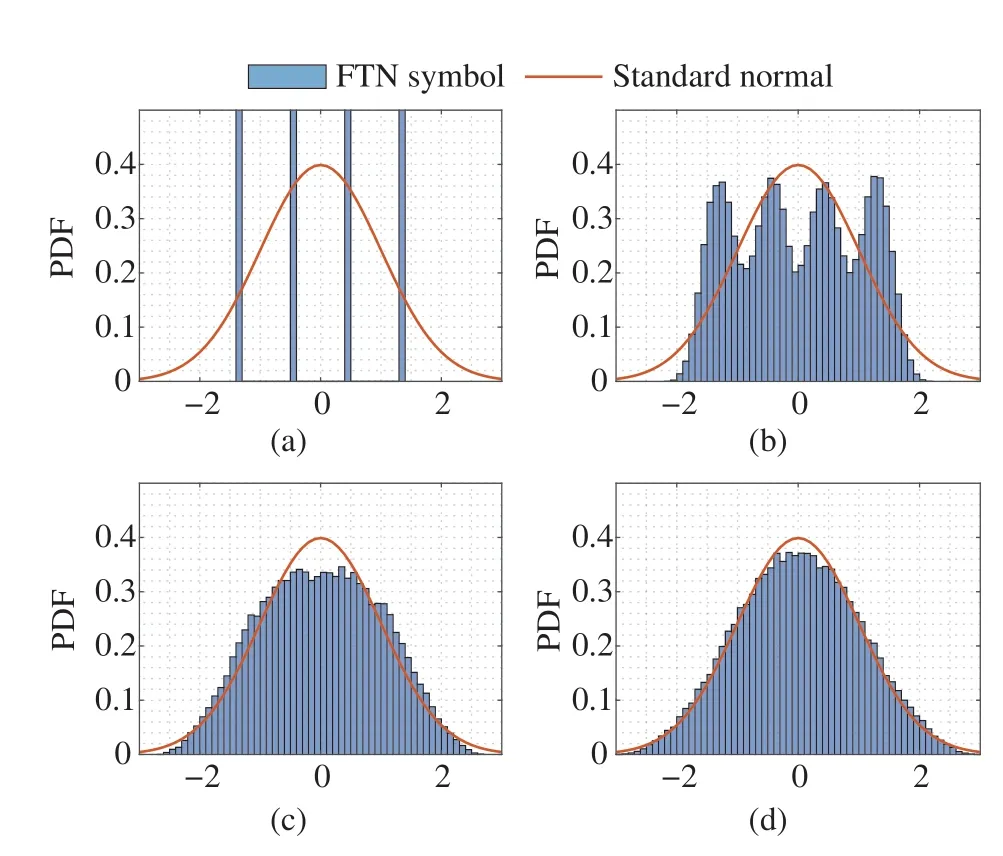
Fig.4 Probability density function(PDF)of FTN symbol and standard normal distribution:(a)τ=1,β=0;(b)τ=0.8,β=0.3;(c)τ=0.6,β=0.3;(d)τ=0.4,β=0.3

The training parameters for the CVDNN system are detailed in Tab.2.And Tab.3 presents a comprehensive comparison of various metrics across different methods.Notably,the complexity evaluation primarily focuses on complex multiplication,and CVDNN can be enhanced performance through parallel computing capabilities.

Tab.2 Parameters for training the CVDNN

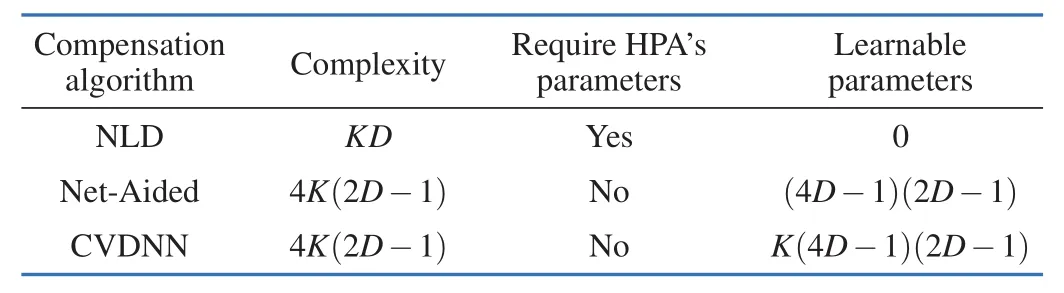
Tab.3 Comparison of various metrics under different methods

The proposed approaches under two different training data sets for nonlinear compensation are compared in Fig.5.Note that‘No HPA’here means that the HPA is not used in the simulation,and we keep the same power level as the HPA case.In the figure,the proposed model-driven approach outperforms the CVDNN-aided scheme and nearly approaches the performance NLD scheme with perfect knowledge of the HPA’s parameters.Our approach has no need for these parameters and is more practical.Especially,the model-driven approach trained with the Gaussian distribution as the training data is proved to be effective.Even though the proposed CVDNNaided scheme is not as good as the model-driven approach,it still compensates for the nonlinear distortion effectively and outperforms the FTN system without compensation.

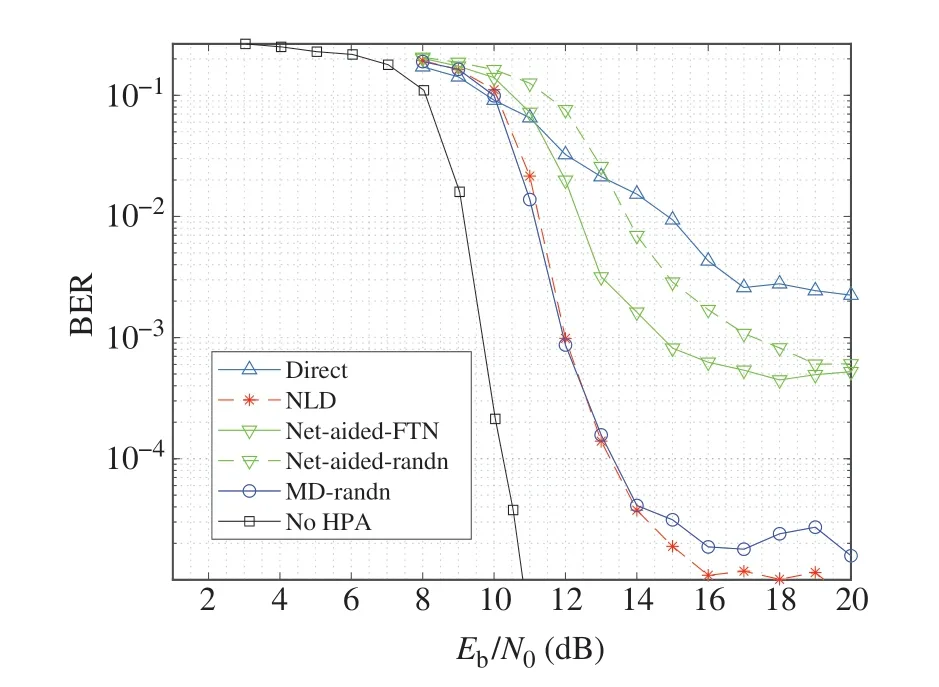
Fig.5 Bit error rate (BER) performance of proposed nonlinear compensation schemes for coded FTN System under different training sets with Rc=2/3,where ‘direct’ means no compensation is applied,‘-randn’ and‘-FTN’ are the proposed schemes with Gaussian and FTN training sets,respectively

A lower rate of the coded FTN system is also considered in Fig.6 withRc=1/2.In this case,the model-driven approach outperforms the NLD approach under different modulation andτ.CVDNN employed in the model-driven approach used the same weights,trained with a Gaussian distribution as the training data,for different modulations andτ.In these instances,the model-driven approach demonstrates superior performance and exhibits greater robustness to variations in the parameters of the FTN system.In terms ofEb/N0,about 0.5 dB gap is observed at BER=10-6.For 8PSK modulation,the FTN signal withτ=0.6 exhibits stronger ISI compared to the FTN signal withτ=0.8.The impact of nonlinearity is stronger,resulting in degraded system performance.Also,the error foor is lower than that in the higher rate case.So the model-driven approach is more suitable for the case of lower rates.

Fig.6 BER performance of model-driven approach working in lower rate with Rc=1/2

This approach can be applicable to orthogonal frequencydivision multiplexing(OFDM)as shown in Fig.7.In OFDM modulation,the model-driven approach exhibits superior performance compared to the NLD algorithm,resulting in a lower error foor.The reason behind this improvement lies in the orthogonality of OFDM symbols,eliminating (ISI) and consequently minimizing nonlinearity.This indicates that the neural network proposed us is also suitable for nonlinear compensation at the receiver end in other systems,such as OFDM.

Fig.7 BER performance of model-driven approach working with OFDM(Rc=1/2,and the number of OFDM subcarriers is 16.)

V.CONCLUSION

In this study,we design CVDNN-aided compensation schemes for the coded FTN system with HPA under unknown HPA’s parameters condition at the receiver.Based on it,we propose a model-driven approach to compensate for the HPA nonlinearity for better performance.We analyze the distribution of FTN symbol and find the Gaussian distribution is a good approximation.Then we design two training sets for the CVDNN-aided and the model-driven schemes.The proposed model-driven CVDNN scheme can achieve a better performance than the NLD approach.Especially,the model-driven approach obtains about 0.5 dBEb/N0gain at BER=10-6for the case of low rateRc=1/2.

The proposed neural network is also applicable for nonlinear compensation in other systems,including OFDM.And FTN with HPA can work well in future Wireless Communication systems,extending the application of FTN.