多轴随机振动下制动器防尘罩失效分析与优化∗
2024-01-05赵礼辉施玉东张东东朱江峰杨万杰
赵礼辉, 施玉东, 翁 硕, 张东东, 朱江峰, 杨万杰
(1.上海理工大学机械工程学院 上海,200093)
(2.机械工业汽车底盘机械零部件强度与可靠性评价重点实验室 上海,200093)
(3.上海市新能源汽车可靠性评价公共技术服务平台 上海,200093)
(4.苏州苏试试验集团公司技术中心 苏州,215000) (5.义和车桥有限公司技术中心 诸城,262200)
引 言
制动器防尘罩是汽车制动系统中保护制动盘的关键部件,特别是在高速工况下,能够有效防止砂石等异物冲击制动盘,提高制动可靠性。防尘罩的早期失效增加了制动盘异常磨损、冲击破裂的风险,严重威胁制动安全性。由于长时间受路面不平度引起的多轴随机振动载荷作用,防尘罩易产生振动疲劳问题[1]。同时,防尘罩的复杂曲面结构使其表现出多样的失效形式,难以通过单一分析手段确定失效原因。准确识别防尘罩失效原因并提出有效的寿命提升方案对保证制动可靠性具有重要意义。
振动疲劳在汽车结构上非常普遍,是影响结构使用寿命的重要因素之一[2-4]。目前,振动疲劳问题的研究方法主要包括时域法和频域法[5-7]。时域法直接基于时间载荷激励下结构的应力历程进行雨流循环计数及寿命预测,适用于处理载荷周期性较强的工况。实际工程结构通常需承受长时间的随机振动载荷作用,此时采用时域法预测寿命代价巨大,不易实现。频域法采用功率谱密度(power spectral density, 简称PSD)来描述随机过程的应力循环,计算量小,在工程实践中得到了广泛应用。
国内外学者基于频域法对工程结构的振动疲劳问题开展了大量的实践研究。Essam 等[8]基于理论分析获得试验级载荷谱,采用单轴逐次加载的方式对某飞机座椅支撑管进行振动疲劳失效试验,确定出失效风险部位,并结合Dirlik 方法计算了结构的疲劳寿命,结果表明,理论计算寿命与实际寿命吻合度较好。戴江梁等[9]结合有限元分析预测了车载电池包托盘结构的疲劳寿命及失效位置,结合试验级载荷谱,通过三轴依次加载的试验方法确定实际失效位置,试验与仿真分析结果较为吻合,并给出了寿命提升的优化设计方案。杨燕等[10]结合Dirlik 法预测了钢丝网套补偿器在随机振动载荷作用下的损伤,确定出损伤最大位置,为结构改进提供依据。刘龙涛等[11]采用有限元方法获取某机载产品的随机振动响应谱,结合Dirlik 法计算结构的疲劳损伤并与试验结果进行对比,验证了频域疲劳计算方法的有效性。上述研究大都采用有限元分析与基于试验级载荷谱的台架试验相结合的方法来分析结构的振动疲劳失效与寿命预测问题,很少考虑多轴载荷间的耦合效应。
笔者针对某制动器防尘罩反复出现早期失效(试验要求寿命的0.5~0.8 倍)问题,基于实测载荷谱提出了一种仿真分析与试验验证相结合的失效分析与寿命提升方法。
1 失效原因分析
1.1 失效模式
某轻型商用车的整车道路耐久试验在通州试验场开展,试验道路总长为6 600 m,其中强化路面占比55%,强化路面类型如表1 所示。试验过程中,制动器防尘罩是特别关注的结构之一,一般通过螺栓固定于转向节端面,服役时不随车轮转动。防尘罩安装状态及关系示意如图1 所示。

图1 防尘罩安装状态及关系示意Fig.1 Installation status and relationship of dust cover
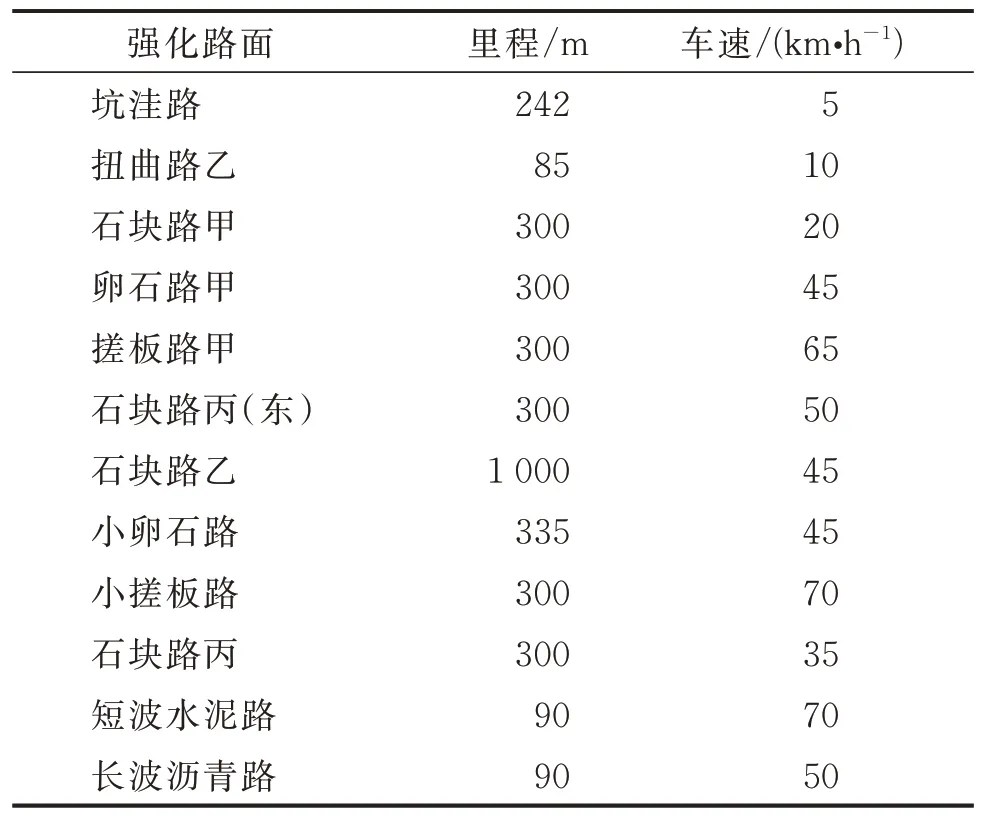
表1 强化路面类型Tab.1 Type of strengthen road
3 辆试验车的前轮制动器防尘罩均在一个耐久循环(450 h)内发生失效,说明失效并非偶然。防尘罩结构失效情况如图2 所示,可以看出,裂纹主要在端平面上的螺栓孔附近萌生、扩展,但防尘罩表面未见明显机械损伤。结合扫描电镜观察断口微观形貌可以发现,图3 所示的裂纹扩展区呈现为疲劳条带,图4 所示瞬断区呈现为撕裂韧窝特征,可知防尘罩结构早期失效模式为典型的金属疲劳失效。

图2 防尘罩结构失效情况Fig.2 Failure mode of dust cover

图3 裂纹扩展区Fig.3 Crack propagation zone

图4 瞬断区Fig.4 Transient breaking zone
1.2 失效原因
1.2.1 载荷采集与特征分析
防尘罩在实际服役时随车轮跳动,承受着路面不平度引起的随机振动载荷,这些载荷是导致防尘罩结构失效的根本原因[12-14],也是失效仿真分析与试验验证的基础输入。在转向节端面布置三向加速度传感器采集随机振动载荷,传感器布置如图5 所示(x向为汽车前进方向,z向为汽车垂直方向)。

图5 传感器布置示意图Fig.5 Sensor layout diagram
以右前轮载荷为例进行特征分析,其原始加速度谱如图6 所示,幅值分布与穿级计数分布分别如图7,8 所示(其中频次为无量纲单位)。可以看出:整车坐标系三向载荷的峰值加速度数值均低于20g,不存在极端冲击载荷,具有疲劳失效载荷的特征;y向总体加速度水平较低,x和z向加速度较大,并且处在相同量级,说明x和z向载荷对结构失效的影响较大。
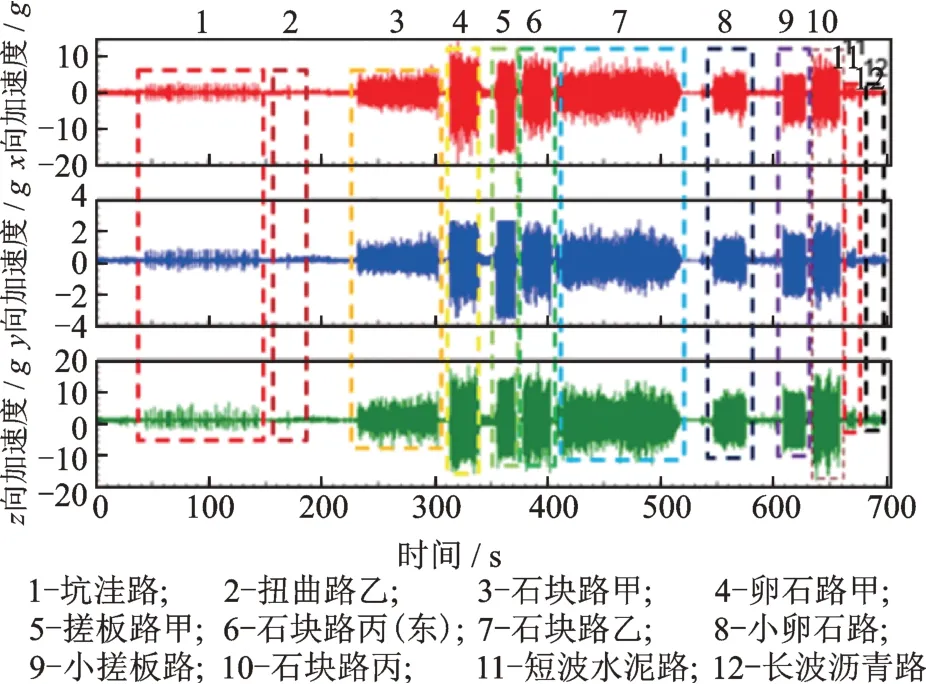
图6 右前轮原始加速度谱Fig.6 Original acceleration spectrum of right front
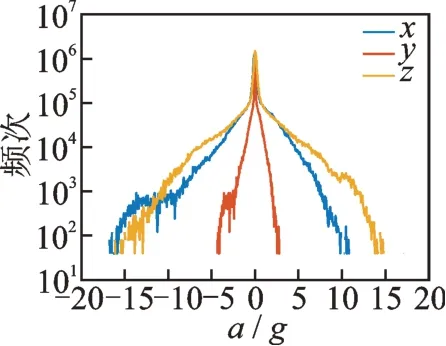
图7 幅值分布图Fig.7 Amplitude distribution diagram
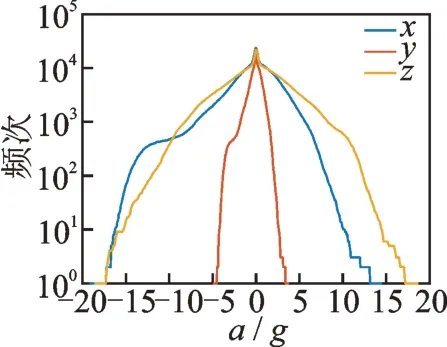
图8 穿级计数分布图Fig.8 Distribution diagram of through-stage count
右前轮加速度载荷的功率谱密度如图9 所示,3个轴向载荷能量均主要集中在20~40 Hz 频率范围内,该频带可能接近于防尘罩的低阶固有频率。相干系数用于表征两随机过程在各频率分量上的线性相关程度[15],三轴向加速度载荷的相干系数如图10所示。可以看出,主要频带的相干系数较高,说明各轴载荷之间存在较大耦合,需要考虑各轴载荷间的相互作用与能量传递引起的损伤。
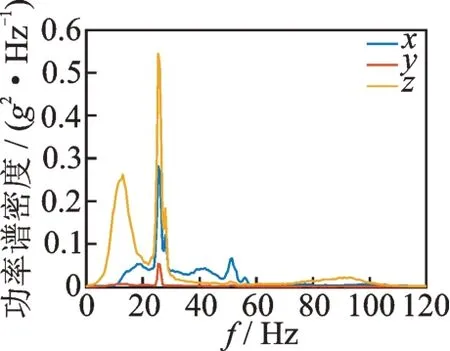
图9 功率谱密度Fig.9 Power spectral density

图10 相干系数Fig.10 Correlation coefficient
1.2.2 基于有限元仿真的失效原因分析
结合实测载荷谱与有限元数值仿真,分析防尘罩的失效原因。对防尘罩的几何形状进行简化,采用壳单元离散化,建立有限元模型,如图11 所示。在3 个螺栓孔处设置Rbe2 单元,用于施加约束和激励载荷。防尘罩的材料为DC01 冷轧钢,弹性模量为210 GPa,屈服强度为130~260 MPa,抗拉强度≥270 MPa,伸长率为32%。
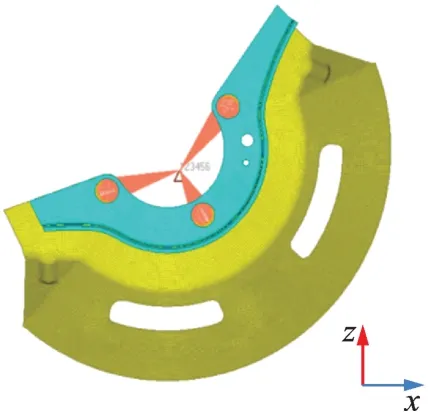
图11 罩有限元模型Fig.11 Finite element model of dust cover
1) 约束模态分析。首先分析了防尘罩的约束模态,考核防尘罩的低阶固有特性及模态应力分布情况。
由载荷的PSD 可知,激励频率主要在60 Hz 以下,因此重点关注防尘罩的低阶模态。防尘罩前4阶约束模态频率分别为42.9,64.1,96.3 和122.6 Hz,其中1 阶、2 阶的模态频率与激励载荷的主频率较为接近,存在低频共振的可能性。从图12 所示的前4阶模态应力云图也可以看出,1 阶、2 阶的应力主要集中在端面的安装孔附近,与实际失效部位一致。因此,防尘罩的失效可能与随机载荷激励下的低频共振相关。

图12 前4 阶模态应力云图Fig.12 Modal stress cloud diagram of first four mode
2) 随机振动响应分析。为进一步明确失效原因,在防尘罩的约束点处施加如图9 所示的加速度PSD 信号,进行随机响应分析,监测结构在多轴随机振动载荷激励下的应力响应,获得防尘罩结构的均方根(root mean square,简称RMS)应力分布及局部应力张量,如图13 所示。从RMS 应力云图可以看出,应力响应较大的单元与实际失效位置具有较好的一致性,RMS 应力最大值为30.7 MPa,出现在右上螺栓孔附近的7394 单元处。
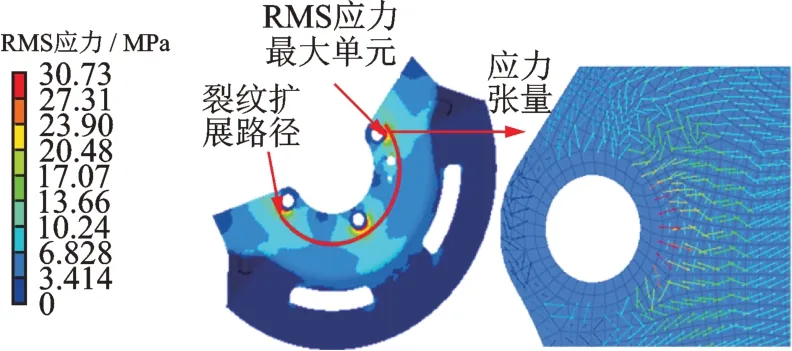
图13 RMS 应力及局部应力张量Fig.13 RMS stress and local stress tensor
图14 为提取的防尘罩有限元模型7394 号单元的应力PSD。可以看出,三向载荷同时作用与x向载荷单独作用时,7394 单元均在结构的1 阶固有频率42.9 Hz 附近出现最大应力响应,而在2 阶固有频率附近只出现1 个较小峰值。同时,从图9 所示的功率谱密度可以看出,x向的载荷在防尘罩的1 阶频率处的量级也远大于y和z方向,这说明单元处的响应主要来源于1 阶固有频率附近的随机振动载荷激励。

图14 7394 单元应力PSDFig.14 PSD stress of element 7394
综上所述,结合模态分析的结果可以确定,防尘罩的失效是由于1 阶模态频率偏低、与道路激励载荷发生低频共振所导致。
2 快速试验验证
基于防尘罩多轴载荷的失效主导载荷分析和损伤等效原则,构建了加速试验载荷谱,采用高加速台架试验,验证基于有限元仿真的防尘罩失效分析的准确性。
2.1 随机振动疲劳分析方法
工程实践证明,Dirlik 方法对随机振动疲劳损伤的预测较为准确[16-18],该方法通过大量数值模拟,将应力循环的幅值概率密度函数归纳为1 个指数分布和2 个Rayleigh 分布。发生在时间T内应力为S的循环次数N(S)的表达式为
其中:
为估算疲劳寿命,需要明确材料的疲劳寿命曲线(S-N 曲线),其常见表达式为幂函数形式[10],即
其中:a,C为材料常数。
根据Miner 线性损伤累积准则,损伤D定义为一定应力等级下载荷循环次数n与该应力等级下材料的寿命N的比值[10],即
联立式(1)~(3),可得随机振动疲劳损伤计算公式为
2.2 多轴载荷降维处理
单轴依次加载方式无法考虑各轴载荷间的耦合效应,而三轴振动试验对试验台要求较高,因此考虑对三轴载荷进行降维处理。分别计算x,y,z向单轴载荷激励下的疲劳寿命,以确定失效主导载荷方向,作为加速试验载荷谱编制依据。
防尘罩的材料为DC01 钢,其S-N 曲线表达式为S7.46N=2.4×1023。结合仿真获得的危险点处应力功率谱密度,再采用式(4)计算单位小时下结构的损伤值,得到的防尘罩损伤结果如表2 所示。可以看出,x向单轴激励时的损伤值远大于其余轴向载荷激励时的损伤值,且与三轴激励时的损伤值在同一量级水平。显然,三向载荷中x向载荷对结构失效的影响最大,因此x向为失效主导载荷方向。

表2 防尘罩损伤结果Tab.2 Damage results of dust cover
2.3 加速试验载荷谱编制与试验验证
振动疲劳试验是对结构进行疲劳分析和验证的有效手段,但直接使用原始载荷的PSD 信号进行台架试验耗时长、成本高,不利于产品的快速验证。结构在振动载荷下的应力响应σRMS与激励gRMS成正比关系,即σRMS=KgRMS,其中K为与结构特性相关的常数,因此可以通过提高PSD 谱的量级来实现振动疲劳加速试验[19]。
基于疲劳损伤等效原则,对原始载荷进行加速处理,加速谱编制流程如图15 所示。主要步骤解释如下:
1) 基于实测的三轴向原始载荷计算整个试验场循环下的总损伤Dt,作为损伤目标;
2) 基于失效主导载荷分析结论,将x单向载荷进行傅里叶变换后,拟合为分段线性的加速PSD 加载谱,计算10 h 的加速损伤值Da;
3) 对 比 损 伤 目 标Dt与10 h 加速损伤Da,当损伤值误差超过5%时,调整加速谱量级,重复上述步骤;当损伤值误差小于5%时,输出PSD 加载谱作为试验加速谱。
依据加速载荷谱的编制流程,获得图16 所示的加速试验载荷谱。以该试验谱为加载载荷,在单轴电磁振动试验台上对防尘罩进行随机振动疲劳试验。采用3 个螺栓将防尘罩安装在工装上以模拟实车约束,随机振动试验如图17 所示。试验过程中重点关注3 个螺栓孔处的结构变化。随机振动试验进行约12 h 后,3 个螺栓孔附近均出现疲劳裂纹,试验失效模式如图18 所示。失效位置与仿真分析及试验场路试结果吻合,说明编制的加速试验谱是有效的,基于有限元仿真的失效原因分析是可靠的。

图16 加速试验载荷谱Fig.16 Accelerated test spectrum

图17 随机振动试验Fig.17 Random vibration test

图18 试验失效模式Fig.18 Test failure mode
3 优化设计与寿命提升
针对防尘罩在路面激励下1 阶共振导致的失效问题,采用形状优化方法,提出优化方案,并通过仿真分析验证优化模型的寿命提升效果。
3.1 形状优化方案
形状优化一般用于在薄壳结构中寻求加强筋的最佳布置方案[20],其本质是将薄壳结构离散化后,对节点坐标进行调整以满足设计目标的要求,并通过调整后的最佳节点位置重构曲面,得到优化后的结构形貌。笔者考虑到防尘罩的结构形式与安装方式,将其结构分为安装区、平面部分和曲面部分,分别对应为非设计空间、设计空间1 及设计空间2,设计空间定义如图19 所示。
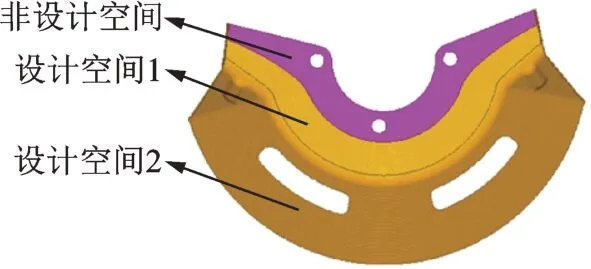
图19 设计空间定义Fig.19 Definition of design space
优化目标为第1 阶固有频率最大化,考虑到加工工艺要求,设置表3 所示的工艺约束参数。分别对2 个设计空间进行优化设计,计算迭代收敛后获得防尘罩结构的起筋变形云图,如图20 所示,其中蓝色区域为加筋参考区。考虑到冲压加工工艺及成本,选取对1 阶固有频率提升贡献较大的加强筋进行布置并进行边缘光滑处理,优化后的防尘罩结构如图21 所示。

图20 起筋变形云图Fig.20 Cloud image of stiffening deformation

图21 优化后的防尘罩结构Fig.21 Optimized dust cover

表3 工艺约束参数Tab.3 Process constraint parameter
3.2 寿命提升验证
对优化模型进行模态分析及疲劳寿命计算。优化后模型的1 阶固有频率提高至53.9 Hz,提升了25.8%。三轴随机振动载荷激励下,防尘罩优化模型的应力响应如图22 所示,应力水平显著降低,结构低频共振现象得到较大改善。同时,三轴载荷激励下的防尘罩疲劳寿命提升至4 782 h,寿命提升了18 倍,寿命提升效果显著。
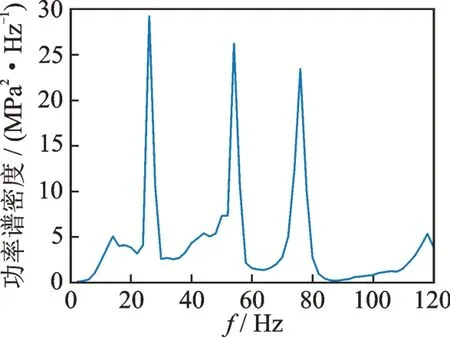
图22 优化模型的应力响应Fig.22 Stress response of the optimized model
4 结 论
1) 制动器防尘罩的早期失效为典型的金属疲劳失效,主要由1 阶固有频率附近载荷的共振所导致。
2)x向振动载荷为防尘罩的失效主导载荷;单轴高加速振动试验结果与有限元分析方法获得的失效原因吻合度较高,验证了高加速试验谱及仿真失效分析的有效性。
3) 形状优化将防尘罩的1 阶固有频率提高了25.8%,三轴振动载荷作用下的疲劳寿命提升了18倍,寿命提升效果显著。
