基于传递路径的整车底板振动优化方法∗

刘雪莱， 赵阳阳， 王 东

（1.上海汽车集团股份有限公司技术中心 上海，201804）

（2.华南理工大学机械与汽车工程学院 广州，510640）

引 言

传递路径分析（transfer path analysis，简称TPA）作为广泛用于车辆系统振动噪声分析的方法［1］，可以对引起车内振动噪声（noise vibration and harshness，简称NVH）问题进行有效的路径分解，识别出引起整车振动噪声的激励源和关键部件，进行有针对性的改进和优化［2］。经典的TPA 方法精度较高，数据稳定性好［3］，但是需要进行大量的传递函数测试，因此周期长、成本高，工程运用推广较为困难。为了解决这一问题，快速TPA、多级TPA 等方法应运而生，但都无法对试验所需资源和周期有实质性的减少［4］。为了克服传统TPA 的弊端，研究人员提出了基于工况的传递路径分析（operational TPA，简称OPA）方法［5］，通过奇异值分解计算各条路径对目标振动的贡献量。该方法不需要通过测试传递函数建立响应矩阵，仅需要实际工况下的数据即可完成，周期短、效率高，但整体计算精度较低，路径间存在耦合时容易出现贡献量丢失的现象［6］。

与前2 种方法不同，扩展工况传递路径分析（operational-X TPA，简称OPAX）方法［7］在计算精度与资源效率间进行了较好的折中，以实测工况数据为主加上少量的传递函数测试，通过等效的集总参数化模型识别出较为精确的工况载荷和各条路径的贡献量。同时，该方法可以实现弹性连接原件的动刚度快速计算［8］。传递路径分析方法发展了数十年，各类方法不断迭代优化，工程中的实际运用越来越广泛［9］。

动力总成作为汽车的动力输出部件，由于本身的燃烧不平衡特性以及变速箱内齿轮啮合特性，是整车NVH 问题最主要的振动源之一，通过悬置、进排气系统及传动轴等部件将振动传递到车内。研究人员通过经典TPA 的方法，建立了从动力总成到车内的传递路径模型，通过台架试验［10］和实车试验［11］识别出动力总成的激励载荷以及传递动力总成振动的关键路径。基于识别出的载荷和路径进行关键部件结构或刚度的优化，从而实现NVH 问题的改善［12］。相类似的研究方法也运用在纯电动汽车中［13］。OPA 方法由于其较高的效率，工程中也运用于快速识别动力总成载荷传递的情况［14］。为了提升计算精度，在进行传函计算时，往往要对信号进行奇异值分析和主惯量分解［15］以减少噪声信号对结果的影响。Landweber 迭代法也被运用于多个激励源的解耦分析，以提升OPA 方法的稳定性［16］。这些方法也能有效地分析动力总成到车身的各条路径对车内噪声的贡献量［17］。OPAX 方法目前在工程中的运用相对较少，主要用于悬置、衬套等元件的刚度识别和载荷分析［2，8，18］。从上述研究可以看出，当传递路径分析迭代优化出全新的方法后，都会被用来分析动力总成对车内引起的振动噪声问题，但研究的重点主要集中在悬置系统中。随着汽车对NVH 性能要求的逐渐提高，与悬置连接的副车架也通过橡胶衬套与车身软连接以降低车内振动，而这一设计使得传递路径系统更加复杂。

笔者针对整车加速过程中底板抖动问题开展研究，建立了包含悬置、副车架衬套在内的整车OPAX模型，利用建立的模型识别出路径中所有橡胶弹性元件的动刚度，计算出工况下各条路径传递的载荷和对底板振动的贡献量，找出引起问题的原因和关键零件。基于分析结果，建立包含动力总成和副车架的动力学模型，以衬套支反力最低为目标对关键路径上的衬套刚度进行优化，并通过整车试验验证了优化效果。

1 OPAX 模型的建立

1.1 实车问题

某款MPV 车型（搭载4 缸机、2.0T+8AT 动力总成）在5 挡50%节气门开度工况下，驾驶室底板存在明显整车x向振动。整车坐标系定义如下：x轴水平向整车行驶后方；z轴垂直向上；y轴根据右手定则确认［19］。加速工况地板x向振动信号如图1 所示。当发动机转速在2 000~2 400 r/min 区间时，底板的前排和中排振动明显加剧，振动总能量（over all，简称OA）值突起，2 阶激励能量分布与OA 值一致，说明此处的振动激励源主要是动力总成的2 阶激励载荷。工程中结合主、客观结果认为，2 阶激励引起的底板振动小于0.15g属于正常可接受范围。由图可以看出：振动峰值在2 050 和2 300 r/min 处，峰值均超过0.15g；随着转速上升到2 400 r/min，振动幅值降低到0.15g以下，恢复到正常水平。

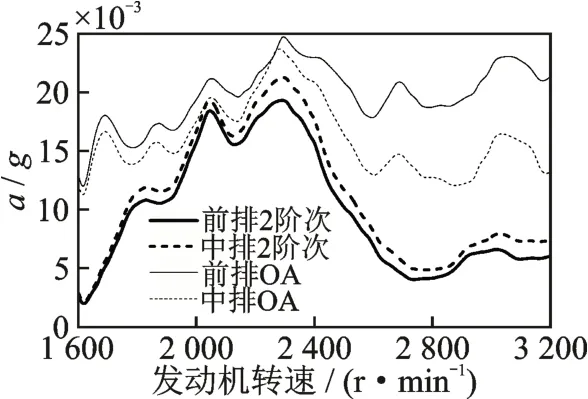
图1 加速工况地板x 向振动信号Fig.1 Floor vibration signal of x-direction under acceleration condition

解决该问题需要分析出各条路径对底板振动的贡献量，找出传递振动的关键路径以及关键零件，提出针对性的优化方案。

1.2 模型建立

由图1 可知，底板振动的转速范围为2 000~2 400 r/min，对应2 阶激励频率为67~80 Hz。在这个频率范围，振动主要是通过结构件传递到车内，在建模时主要考虑结构传递路径。

问题车辆动力总成是通过发动机悬置、变速箱悬置与车身连接，并通过一个下拉杆与副车架连接。为了改善整车NVH 品质，提升副车架的隔振能力，通过4 个衬套连接副车架与车身。整车传递路径及响应点如图2 所示。

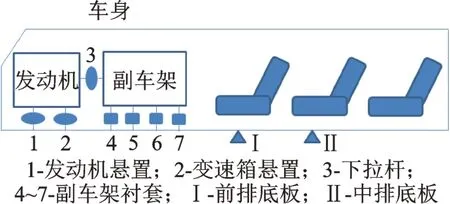
图2 整车传递路径及响应点Fig.2 Transmission path and response point for vehicle

基于“激励源-传递路径-目标响应点”的简化分析模型，假设从动力总成一共有n条路径传递振动到车内，则到车内第q个响应点［2］有

其 中：yq(ω) 为 第q个 响 应 点 的 振 动 量；Gqj(ω)，Fqj(ω)分别为第j条路径到第q个响应点的传递函数（frequency response function，简称FRF）和第j条路径的实际工况载荷；ω为动力总成的激励频率。

弹性元件（悬置、衬套）的主要材料都是天然橡胶，其自身动刚度远低于主、被动侧的金属件。建立“刚度-阻尼-质量”模型对动刚度进行等效［6］，即

其中：Kj(ω)为第j条路径弹性元件的动刚度；mj，cj，kj分别为弹性元件的等效质量、阻尼和刚度。

基于弹性元件动刚度法求解载荷的原理［11］，结合式（1）、式（2）可知，第q个响应点的振动量为

其中：aaj(ω)，apj(ω)分别为弹性元件主、被动侧的振动加速度。

在实际计算过程中，对不同转速、不同阶次下采集到的响应点的响应值以及弹性元件的主、被动侧振动加速度进行分析，利用最小二乘法拟合出所有弹性元件的“刚度-阻尼-质量”模型参数［10］，进而实现刚度的识别以及各路径贡献量的分析。

每个悬置或衬套在空间中都包含x，y，z这3 个振动传递方向，此处坐标方向与整车坐标系方向相同［11］。动力总成通过2 个悬置和4 个副车架衬套将振动传递到底板，共计6×3=18 条路径。所有路径均为橡胶元件连接，具体的工况载荷均可由式（2）计算得到。目标响应点选择主观评估存在抱怨的底板前排和中排，建立的OPAX 传递路径模型如图3 所示。

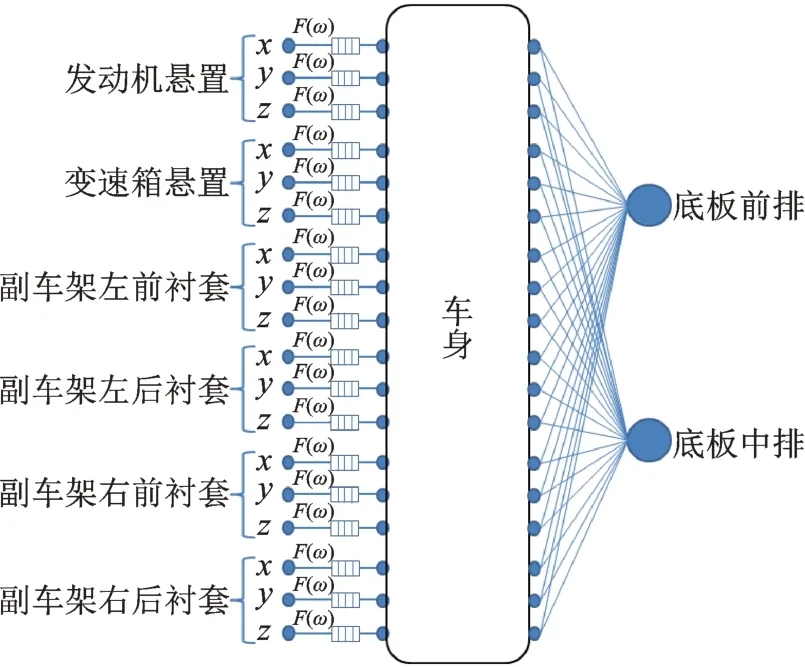
图3 OPAX 传递路径模型Fig.3 OPAX transfer path model

2 实车试验及结果分析

2.1 试验数据采集

为了识别出各条路径的悬置、衬套动刚度以及计算出对底板振动的贡献量，需要进行的试验有：①各条路径到车内响应点的频响函数；②运行工况下各路径和响应点数据。

在测量各路径到响应点频响函数时，要拆除动力总成以及副车架。2 个悬置仅保留与车身纵梁连接的金属外壳，4 个衬套仅保留内管以及与车辆连接的螺栓。在响应点布置加速度传感器，采用力锤逐个敲击悬置的金属外壳和衬套内管，敲击点尽可能靠近悬置、衬套的弹性中心点。

传递函数结果如图4 所示，是所有x向路径点到前、后排响应点x向的FRF，数值越大表明单位力引起的响应越大。由图可以看出：前、后排底板对副车架左前、左后及右后衬套x向激励最敏感；所有路径的FRF 值在67~80 Hz 范围内都低于目标值。

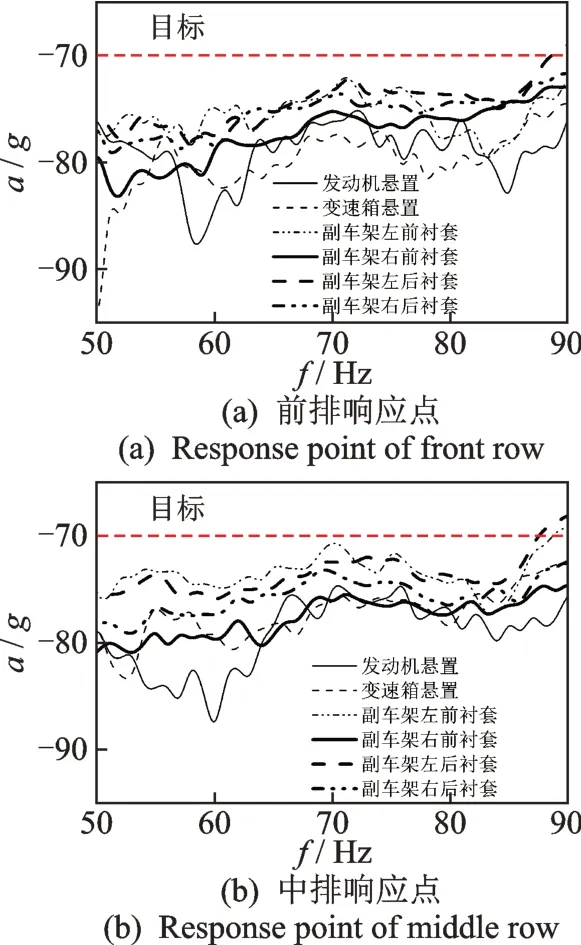
图4 传递函数结果Fig.4 Test result of FRF

在底板振动响应点以及各传递路径的悬置和衬套的主、被动侧布置加速度传感器，采集不同节气门开度条件和车辆整个加速过程中各位置的振动加速度信号。加速度传感器布置如图5 所示，加速工况副车架左后衬套x向振动如图6 所示。

图5 加速度传感器布置Fig.5 Acceleration sensor arrangement

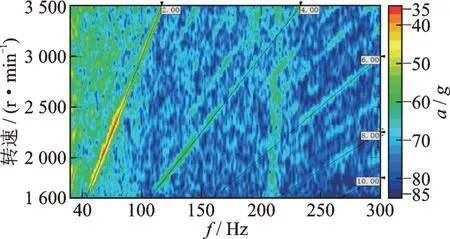
图6 加速工况副车架左后衬套x 向振动Fig.6 Vibration of rear left bush of subframe in x direction under acceleration condition

2.2 载荷识别及贡献量分析

利用上节试验得到的结果进行计算，得到各条传递路径的载荷、贡献量以及弹性元件的动刚度。通过式（1）仿真得到底板2 阶振动量，加速工况地板x向2 阶振动对比如图7 所示。由图可以看出，仿真结果与试验结果一致性较好，2 050 和2 300 r/min两处峰值误差分别为0.2%和4.1%。

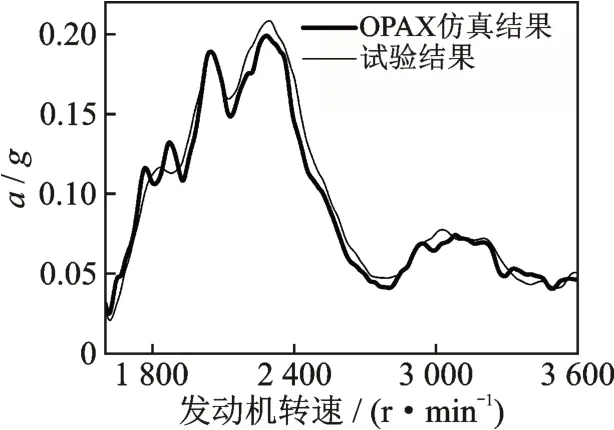
图7 加速工况地板x 向2 阶振动对比Fig.7 Comparison of 2-order vibration of floor in x direction under acceleration condition

为了验证模型的准确性，对副车架衬套进行动刚度试验，并与通过OPAX 方法计算出的衬套刚度进行对比，副车架左后衬套z向动刚度如图8 所示。在50~400 Hz 范围内，衬套刚度计算值与试验值误差都在5%以内，验证了模型的准确性。

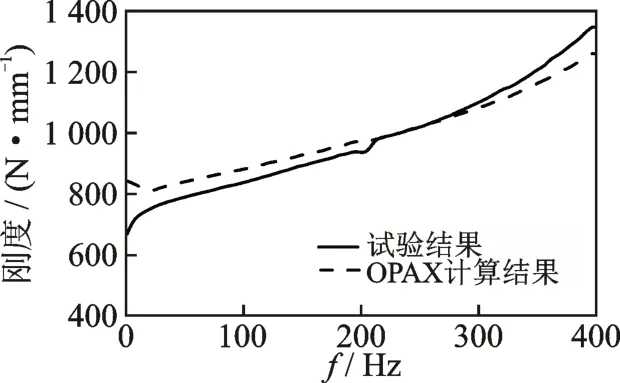
图8 副车架左后衬套z 向动刚度Fig.8 Dynamic stiffness in z direction of left rear bush

底板振动主要是由于x向路径引起，y和z向路径贡献量较小。各路径x向对底板中排振动贡献量如图9 所示，各路径x向峰值处载荷如图10 所示，副车架左、右后衬套x向载荷如图11 所示。2 050 和2 300 r/min 两处问题转速振动贡献量最大的路径均为副车架的左、右后衬套。2 050 r/min 处左后衬套的x向路径贡献量超过20%，2 300 r/min 处右后衬套x向路径贡献量达到30%。

图9 各路径x 向对底板中排振动贡献量Fig.9 Contribution of each path to vibration of middle row of floor at x-direction

图10 各路径x 向峰值处载荷Fig.10 Load peak value of each path at x-direction

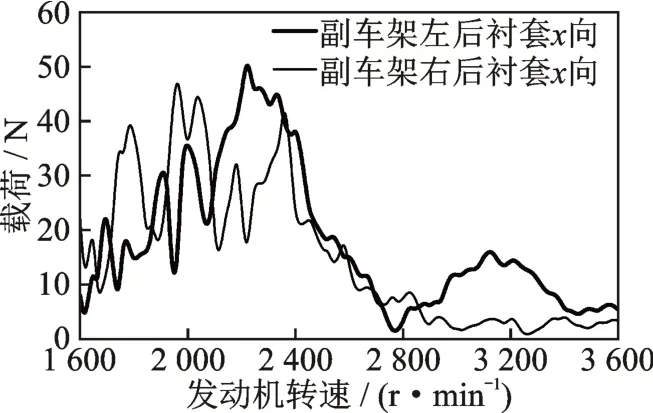
图11 副车架左、右后衬套x 向载荷Fig.11 x-direction load of left and right rear bushing of subframe

由式（1）可知，贡献量是由载荷和FRF 乘积决定的。所有路径的FRF 均未超过设计目标值，表明底板的振动主要是由于路径传递载荷过大所引起。由图10，11 可以看出：副车架的左、右后衬套载荷明显大于其余路径，与贡献量结果一致；在问题转速附近，这2 条路径载荷达到了50 N，而在其余转速范围的载荷均低于20 N；车辆x向底板振动是由于副车架的左、右后衬套载荷过大所引起。

对副车架进行模态试验，在副车架框架上布置10 个加速度传感器，并用激振器激励副车架与下拉杆悬置的连接点，激励得到的副车架FRF 总和以及识别出的副车架模态结果分别如图12 及表1 所示。副车架在67.5 和80.1 Hz 存在2 阶阵型x向平动的刚体模态，与问题转速对应的发动机2 阶激励频率相对应。副车架和衬套系统的刚体模态是引起路径载荷过大的原因。

表1 副车架模态结果Tab.1 Modal results of subframe

图12 副车架FRF 总和Fig.12 FRF sum of subframe

3 底板振动优化

副车架的刚体模态由副车架本身质量、惯量及连接衬套的刚度决定。由于副车架设计空间、结构材料等很难更改，因此通过搭建动力学模型，对衬套刚度进行优化，来实现对动力总成振动的衰减以及对底板振动的控制。

3.1 12 自由度动力学模型的建立

为了研究副车架衬套刚度对动力总成振动的控制影响，建立了考虑动力总成和副车架的12 自由度动力学模型，如图13 所示，模型中分别包含了动力总成、副车架的6 个自由度。发动机悬置、变速箱悬置、副车架4 个与车身连接的衬套接地，下系杆两端分别连接动力总成和副车架。分别在动力总成和副车架的质心建立坐标系Oe-xeyeze和Os-xsyszs，方向参考整车坐标系。

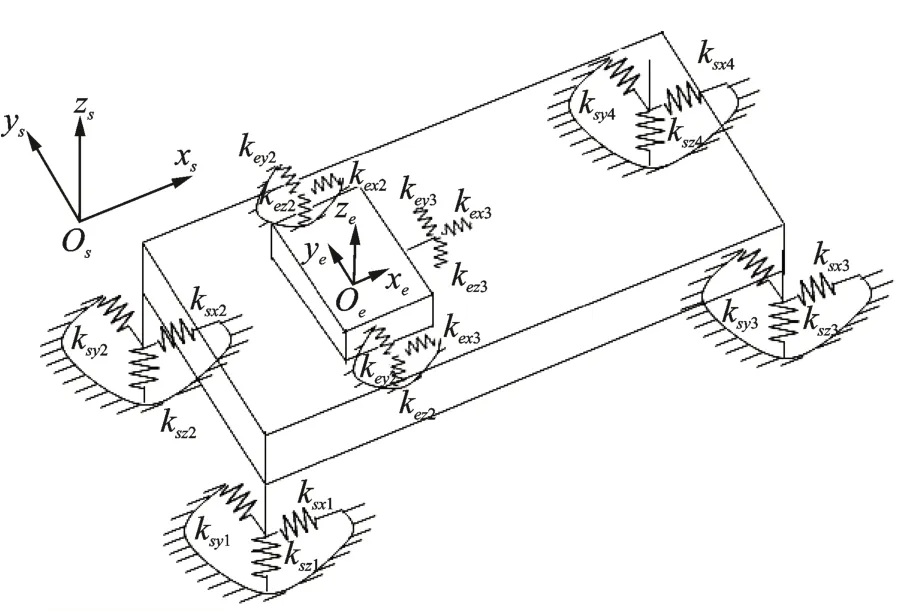
图13 12 自由度动力学模型Fig.13 12 degrees of freedom models

静平衡状态下动力总成以及副车架的3 个平动、3 个转动位移分别为：qeT=（xe，ye，ze，αe，βe，γe）；qsT=（xs，ys，zs，αs，βs，γs）。对于模型中第i个悬置和第j个衬套，在其局部坐标系Oei-xeiyeizei，Osj-xsjysjzsj的刚度、阻尼矩阵分别为kei=diag（kexi，keyi，kezi），ksj=diag（ksxj，ksyj，kszj）和cei=diag（cexi，ceyi，cezi），csi=diag（csxj，csyj，cszj）。

基于坐标转换矩阵，建立在动力总成激励下各个悬置、衬套相对于发动机和副车架的相对位移量［20］。基于位移量计算结果，建立模型的动力学分析方程为

其中：qT=［］；Me，Ms分别为动力总成和副车架的惯性质量矩阵［19］；Fe为发动机输出激励；Eei，Esj分别为第i个悬置和第j衬套的坐标转换矩阵［19］。

忽略系统阻尼，根据式（4）可以计算出动力学模型的系统模态，副车架模态仿真与试验结果对比如表2 所示。可以看出，各阶模态频率计算与试验的一致性较好，误差均小于4%，验证了模型的准确性。

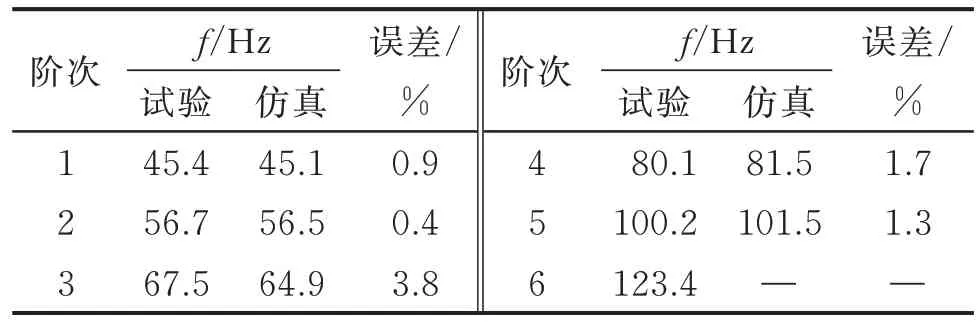
表2 副车架模态仿真与试验结果对比Tab.2 Comparison of modal simulation and test results of subframe

3.2 系统优化

利用所建立的模型研究衬套刚度对整个加速过程中底板振动的影响。在模型动力总成曲轴中心处施加绕y轴的单位扭矩扫频激励，计算整个扫频过程中副车架左后衬套的动刚度，其支反力仿真结果如图14 所示。由图可以看出：在67.5 和80.1 Hz 这2 个副车架刚体模态频率处，衬套x向和z向均出现峰值；x向支反力明显大于z向支反力，这是由于两处模态频率对应的阵型均表现为x向平动。

图14 副车架左后衬套支反力仿真结果Fig.14 Simulation results of reaction force of left rear bush of subframe

考虑到发动机在常用转速条件下主阶次激励频率范围内（50~100 Hz），副车架存在至少2 阶模态，以2 个副车架后衬套x向2 个模态频率处支反力最小为目标进行优化，则优化目标函数为

其中：fzx1，fzx2为车架后衬套x向2 个模态频率处支反力峰值；L1，L2为权重系数，本研究取L1=L2=0.5。

以副车架与车身相连的4 个衬套的x向和z向刚度为设计变量进行优化，即

考虑到车辆左右受载平衡，2 个前衬套之间和2 个后衬套之间的三向刚度需要保持一致。此外，衬套x向和z向刚度分别承担着整车平顺性和支撑性，变化范围不能超过-30%~80%，因此优化模型的约束条件为

其中：0.7ksx1≤ksx1≤1.8ksx1；0.7ksz1≤ksz1≤1.8ksz1。

采用序列二次规划法对所建立的优化模型进行参数优化，优化前后设计参数对比见表3。优化前后副车架后衬套x向支反力对比见图15。可以看出：优化后2 个副车架刚体模态频率分别从67.5 和80.1 Hz 移动到了76.0 和83.5 Hz；2 个频率的支反力峰值分别下降了45.8%和17.1%，优化效果明显。

表3 优化前后设计参数对比Tab.3 Comparison of design parameters before and after optimization N/mm

图15 优化前后副车架后衬套x 向支反力对比Fig.15 Comparison of x-direction reaction force of rear bushing of subframe before and after optimization

3.3 实车验证

基于上一节的结果对衬套刚度进行改进并装车验证。优化前后加速工况地板x向振动对比如图16所示。可以看出：与优化前相比，前排和中排振动峰值分别降低了32%和36%；驾驶员主观分析无抱怨；振动峰值转速移动到了2 320 r/min，对应发动机2 阶激励频率为77.3 Hz，与仿真计算的频率76 Hz 误差仅为1.7%。仿真模型得到了进一步验证。

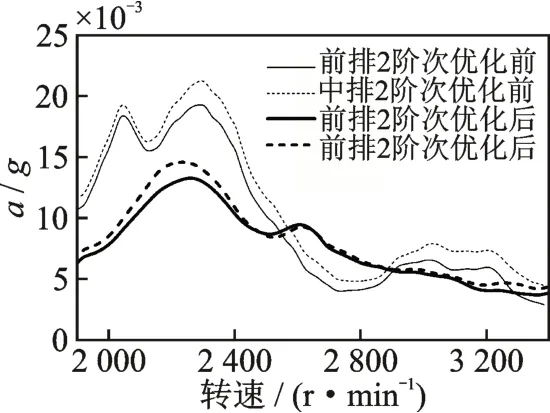
图16 优化前后加速工况地板x 向振动对比Fig.16 Comparison of floor x-direction vibration under acceleration condition before and after optimization

4 结 论

1） 针对车辆在加速时产生的底板振动开展研究，基于扩展工况传递路径分析方法，建立动力总成-副车架-车身OPAX 分析模型，通过模型仿真得到的振动峰值以及衬套动刚度与试验的误差均在5%以内。

2） 引起2 050 和2 300 r/min 两处转速底板振动的关键路径是副车架与车身连接的左、右后衬套x向。结合模态试验发现，副车架在67.5 和80.1 Hz存在2 阶阵型x向平动的刚体模态，与问题转速对应的发动机2 阶激励频率一致，使得在这两处转速下左、右后衬套x向支反力过大，引起底板振动。

3） 建立包含动力总成、副车架以及衬套的12 自由度动力学模型，通过对比模型计算及试验得到的模态频率，验证了模型的有效性。利用模型对衬套刚度进行优化并进行实车验证，结果表明，与优化前相比，前排和中排振动峰值分别降低了32%和36%，优化效果明显。