形状记忆合金变刚度软作动器设计∗

任 旭， 杨书吉， 文 浩， 金栋平

（南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016）

引 言

机器人通常由刚性部件通过控制系统、驱动机构及关节等来完成各种复杂的动作［1］。为适应不同的工作环境和特定的任务需求，完全由刚性部件构建的机器人则难以胜任［2］。受到自然界生物的启发，人们越来越趋于采用具有极低刚度与高适应性的软作动器来代替刚性抓取器，如生物肌肉［3］、章鱼触手和啄木鸟的脖子［4］等。

目前，软作动器有多种驱动形式。例如，气泵软作动器通过内部气压调节实现变形并维持形状［5］；线缆驱动的软作动器是通过电机带动线缆来驱使软作动器变形［6］。然而，这类作动器需外置动力装置，不够轻便。基于电活性聚合物的作动器驱动力小、寿命短且响应时间长［7］。工业上广泛使用的压电材料也可被用于软作动器，但压电材料变形有限，同时驱动电压较高［8］。此外，形状记忆聚合物（shape memory polymer，简称SMP）因具有变刚度的特性也被用于软作动器中，但SMP 自身刚度较低，很难用于抓取大质量物体［9］。

作为一种智能材料，SMA 凭借超弹性、记忆效应、良好阻尼特性和耐腐蚀等性能得到广泛应用［10-11］，尤其是极高的驱动力质量比及快速响应能力使其非常适合作为软作动器的驱动元件［12-14］。潘浩等［15］利用SMA 丝的大驱动力设计了一种可弯曲的机构用于探测领域。Li 等［16］提出通过加热固定的SMA 丝来实现可变刚度。Rodrigue 等［17］研究了如何利用SMA 丝来获得较大的初始变形角度。Lee 等［18］利用SMA 丝模拟肌腱以形成像肌肉一样的往复变形。Kim 等［19］提出利用多组SMA 驱动器模仿鱼鳍运动的装置。Simone 等［20］利用SMA 线束来构建柔软的机械手指，以获得更高的驱动力。Wang 等［21］在SMA 驱动的机械手指关节处嵌入SMP，在变形时呈现低刚度，在抓取物体后呈现高刚度。针对目前SMA 作动器的研究，其样机或由多种驱动形式组成，或过于复杂，并且在形变恢复、提高整体结构的刚性和承载力方面缺乏相应的研究。

笔者提出一种制备简易的可变刚度软作动器，以聚二甲基硅氧烷（polydimethylsiloxane，简称PDMS）为基质，采用嵌入式设计，确保表面被柔软的基质覆盖。作动器使用2 根SMA 丝，一根嵌入到聚合物基质的偏心位置以驱动作动器，另一根嵌入聚合物基质的中性层以实现可变刚度。同时，采用聚氯乙烯（polyvinyl chloride，简称PVC）薄板提高结构的整体刚度并帮助作动器快速恢复变形。理论和实验表明，提出的SMA 丝一维本构理论能够准确预测实际的弯曲变形，作动器恢复形变的能力较好，且通过调节刚度可以提升作动器的负载能力。

1 机理与模型

1.1 一维本构模型

采用Brinson［22］提出的SMA 丝一维本构力学模型，即认为马氏体相变过程为应力引起的相变过程与温度引起的相变过程所组成，可以很好地描述低温下SMA 的力学行为。

Brinson 一维本构模型为

其中：σ，σ0分别为当前和初始状态应力；E为SMA弹性模量；ε，ε0分别为当前和初始状态应变；Ω=-EεL为相变系数，εL为最大可恢复应变；Θ为热膨胀系数；ξ，ξ0分别为当前和初始状态的马氏体体积分数；T，T0分别为当前和初始状态的温度。

等温加载并考虑初始条件为σ0=0，ε0=0，ξ0=0 和T=T0，式（1）简化为

其中

其中：Ea，Em分别为奥氏体与马氏体弹性模量。

当SMA 材料中奥氏体向马氏体转变时，马氏体体积分数为

当SMA 材料中马氏体向奥氏体转变时，马氏体体积分数为

其中：Ms，Mf分别为马氏体相变的起始温度和结束温度；As，Af分别为奥氏体相变的起始温度和结束温度；Cm，Ca分别为马氏体和奥氏体相变极限曲线的斜率，被用于相变曲线拟合。

通过式（2）、式（5）和式（6），并结合表1提供的SMA材料相关参数，即可获得室温下（298 K）与高温下（358 K）的一维形状记忆合金本构关系，如图1所示。

表1 SMA 材料相关参数Tab.1 Material parameters of SMA

图1 形状记忆合金本构关系Fig.1 Constitutive relationship of SMA

由图1 可以看出，SMA 在不同温度下产生同样应变所需要的应力是不同的。室温下，SMA 受到140 MPa 的应力就开始发生大的应变；高温下，则需受到大于620 MPa 应力才能发生大的应变。利用这一特性，可以通过调节SMA 温度来控制其刚度水平。

1.2 作动器变形

作动器主体采用PDMS，内部嵌有2 根SMA 丝与聚氯乙烯（PVC）薄板。其中：SMA-1 用于作动器驱动，并作预应变处理（室温下拉伸至最大可恢复应变状态）；SMA-2 用于实现可变刚度。

变刚度软作动器的横截面结构如图2 所示，其中：作动器长度L=100 mm，宽度w=15 mm，厚度t=5 mm；SMA-1 直 径d1=0.2 mm，SMA-2 直 径d2=0.3 mm；PVC 板厚度tPVC=0.8 mm。

图2 变刚度软作动器的横截面结构Fig.2 The cross-section structure of variable stiffness soft actuator

定义SMA-1 与中性层距离为t1，作动器下表面到中性层距离为t2，PVC 板对称面到中性层距离为t3，SMA-2 直接铺设于PVC 板上表面。由于中性层位置需计算后得到，这几个参数属于未知量。设计时可确定的量有：SMA-1 到作动器下表面的垂直距离t4=t2-t1=0.5 mm；PVC 板对称面到SMA-1 丝的垂直距离t5=t1+t3=2.4 mm； SMA-1 与SMA-2之间的垂直距离t6=2.55 mm。

首先，确定结构中性层位置。根据静力学关系，横截面上的应力满足

将式（7）展开，有

其 中：EPVC，Ea和EPDMS分 别 为PVC 板、SMA-2 丝 和PDMS 基体的弹性模量；APVC，ASMA-2和APDMS为相应部分的面积；y为dA到中性层的垂直距离。

弹性模量和面积由表1 确定，通过式（8）可以获得结构参数t1，t2和t3，继而确定中性层的位置。

由于SMA-1 丝是经过预处理之后嵌入的，具有初始残余应变εL，而同一层面的聚合物基质无应变。经加热相变后，SMA-1 仍有一定应变，可以作为驱动力的来源。此时，SMA-1 丝的应变为εSMA-1，故同一层面聚合物应变为

对于轴向压缩，有

其 中：εaxis为 轴 向压应 变；σSMA-1为εSMA-1所 对 应 的应力；ASMA-1为SMA-1 丝横截面积。

由于轴向压缩变形，作动器中无应力层并非纯弯曲时的中性层。在纯弯曲下，受拉力作用的一侧存在一个位置，该位置的拉应变与轴向压应变相等。设此位置到中性层的距离为t0，则

其中：W为作动器的抗弯刚度。

其中：IPVC，IPDMS和ISMA-2分别为PVC 板、PDMS 基质和SMA-2 丝相对各自对称轴的惯性矩。

根据式（11）和式（12），可以获得零应力位置到中性层的距离t0。根据弯曲变形的几何特性，有

其中：θ为需求解的弯曲角度。

由于ε0未知，无法求得θ，需要与ε0有关的约束条件。考虑到开始定义ε0时是通过SMA-1 处的实际应变计算得到，故通过实际变形计算得到的应变应该与ε0相等，故

根据式（11）、式（13）和式（14），可以得到σSMA-1和εSMA-1的关系，以及与之对应的θ，再通过Brinson一维本构模型获得平衡点，其对应的θ即为变形时的弯曲角度。SMA 丝与作动器弯曲时的应力-应变曲线如图3所示，其中：实线为SMA-1丝的应力-应变关系曲线；虚线为作动器弯曲时的应力-应变曲线。两者交汇处即为平衡位置，即最大变形角度约为101°。

图3 SMA 丝与作动器弯曲时的应力-应变曲线Fig.3 Stress-strain curve of SMA and actuator bending

2 作动器制备

为了在固化PDMS 的同时固定嵌入的元件，需要相关模具。模具由3D 打印制造，选用立体平版印刷（stereo lithography appearance，简称SLA）技术，材料为类ABS 光敏树脂。

作动器制备流程如图4 所示。为方便脱模，模具主体分为两部分，中间夹层为聚丙烯薄膜。由于PDMS 材料与表面光滑的材料黏附性不高，固化后的PDMS 容易脱模，如图4（a）所示。

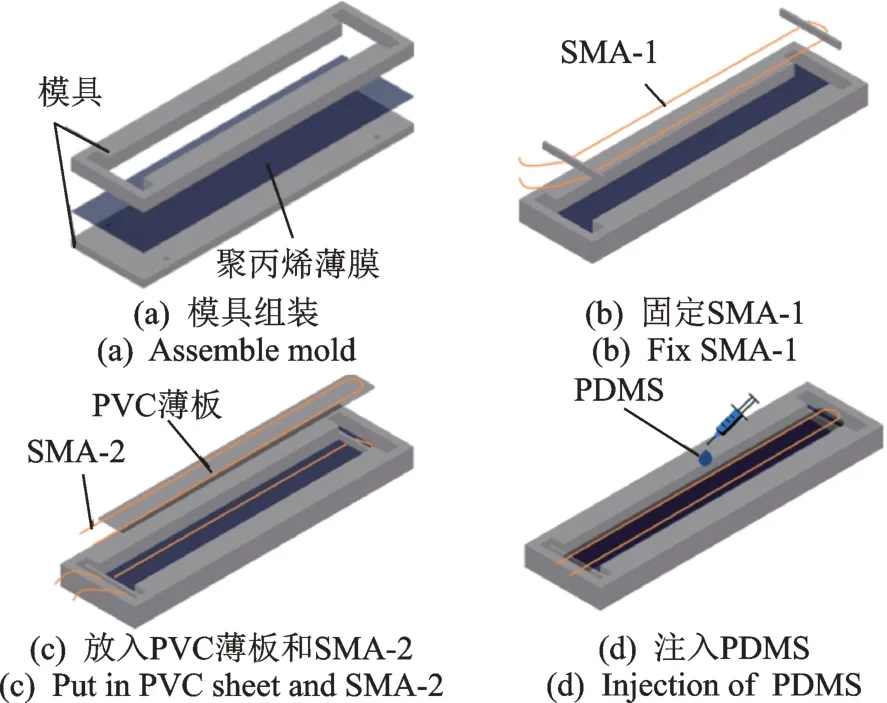
图4 作动器制备流程Fig.4 Manufacturing process of the actuator

模具组装完成后，嵌入元件，包括SMA-1，SMA-2 以及PVC 薄板。为了将SMA-1 精确嵌入到PDMS 基质中，设计了凹槽部位，将预应变SMA-1穿过3D 打印的通孔部件，嵌入到凹槽中，以实现位置固定，如图4（b）所示。

将SMA-2 与PVC 薄板一起放入模具中，并穿过SMA-1 的通孔部件进行定位，如图4（c）。

模具装配完成后，将SMA 丝固定，再注入PDMS。制备所用的PDMS 材料来源于道康宁公司。将PDMS 与催化剂以10∶1 质量比混合，混合过程尽量慢，以避免产生更多的气泡，并静止30 min 使其中气泡消去，再注入到树脂模具中，见图4（d）。

最后，将注入PDMS 的模具在50℃恒温下固化10 h。固化完成后脱模，得到所制备的软作动器。

3 实验结果

使用直流电源（KORAD KA3005D）对作动器的SMA-1 进行通电加热（此时SMA-2 不通电），加载电流从零开始逐渐增大，并在每次改变电流后给予作动器30 s 以达到稳态，直至电流增大到作动器的弯曲角度不再发生明显变化为止。

实验表明，当加载电流到0.8 A 时，继续增大电流，作动器弯曲角度变化不明显，此时最大弯曲角度如图5 所示，θmax=114°，与理论计算结果有13%的误差。产生差异的原因除了模型的简化，还因为计算参数和实际参数有差异，主要是SMA 材料给出最大可恢复应变εL要小于实际预应变处理的值。

图5 作动器最大弯曲角度Fig.5 Maximum bending angle of actuator

逐渐降低施加的电流载荷直至回到零，并在每次改变电流后给予作动器120 s 的时间以达到稳定状态，记录作动器的弯曲角度，从而得到整个升-降温过程中作动器的角度曲线。同样，为了进行对比，另一个作动器去除PVC 薄板与SMA-2，仅嵌入1 根用于驱动的SMA-1 丝（简称单SMA 丝作动器），重复上述过程，可获得另一条曲线，即图6 所示的作动器弯曲角度与电流的关系。可以看出，仅对SMA-1加热的情况下，两者在升温过程中表现出的力学性能基本一致，在降温过程中则存在较大差异。主要原因为：①制备的作动器相较于单SMA 丝作动器，松开的响应时间更快；②制备的作动器恢复形变能力更强，有约5°的残余变形，而单SMA 丝作动器有20°以上的残余变形。

图6 作动器弯曲角度与电流的关系Fig.6 The bending angle of actuator versus the current

在验证了作动器的变形能力后，将3 个作动器结合起来实现物体抓取功能，其照片如图7 所示。

图7 3 个作动器抓取物体照片Fig.7 The photo of grabbing objects by three-actuators

为测试作动器的负载能力，这里使用霍丁格必凯公司的S 型拉力称重传感器，通过测试作动器水平方向的拉力进行衡量。将作动器末端与拉力传感器相连，由于末端受到约束的作用，驱动作动器时会产生水平方向上的拉力。功率放大器与数据采集使用QuantumX MX840，分析软件为catmanAP。为同时给SMA-1 和SMA-2 通电，实验中使用2 台DC 电源独立供电（KORAD KA3005D 和PEAKMETER PM3005B）。

给予SMA-1 丝足以产生相变的电流， 约15 s后，温度基本达到平稳状态，测量记录该过程的拉力数据。在预先给SMA-2 丝通电和使用单SMA 丝作动器的情况下，重复以上操作，共可得3 条拉力曲线，水平拉力变化如图8 所示。在给SMA-1 通电后，蓝色曲线为单SMA 丝作动器的受力曲线；红色曲线为SMA-2 不通电情况下的受力曲线；绿色曲线为SMA-2 通电情况下的受力曲线。可以看出，在SMA-2丝通电的情况下，水平拉力有约25%的提升，表明高温下的SMA-2使得作动器的承载能力更好。

图8 水平拉力变化Fig.8 Horizontal tension versus time

4 结 论

1） 利用SMA 丝在一定应变范围内表现出的高温时大刚度、常温时低刚度特性，将其搭载于聚合物基质中，设计制作了一种新型软作动器。

2） 制备出的新型软体作动器实现了最大变形角度为114°的大变形能力。

3） 通过嵌入PVC 薄板提高了作动器的恢复形变能力，用于可变刚度的SMA-2 丝，提高了作动器的负载能力。