考虑个体差异效应的高拱坝测点群变形监控∗

杨 光， 孙 锦， 赵阿辉， 林海波， 王 琳

（1.华北水利水电大学水利学院 郑州，450046）

（2.河海大学水文水资源与水利工程科学国家重点实验室 南京，210098）

（3.华北水利水电大学测绘与地理信息学院 郑州，450046）

引 言

我国西部地区已建或在建一批高拱坝，这些巨型工程既带来了巨大的效益，也引起了严峻的安全问题。由于失事后果的灾难性，高拱坝安全受到广泛和密切的关注［1-2］。变形是高拱坝结构性态动态变化的直观反映，亦是衡量安全状况的一项重要指标。采取有效的变形监控措施，有助于技术人员及时捕捉到异常现象，确保工程安全运行［3-5］。

HST 模型［6-7］常用于监控拱坝变形变化，其将拱坝变形归结为3 个分量：水压和温变分量体现了主要荷载作用下的变形瞬时效应；时效分量则反映了徐变、蠕变等因素影响下的变形时变效应。目前，HST 模型已向纵深发展［8］，神经网络、深度学习等现代数学理论被引入，依托HST 的复合建模、多点建模等新理念也相继被提出。总体来看，多数研究着重考察了高拱坝单点变形变化，对变形空间分布、各部位变形间相互影响等隐含特征考虑较少，而这些隐含特征却包含有高价值的状态信息。

受到边界约束、结构型式、地质条件、材料性质及荷载的综合影响，高拱坝变形变化呈现出群体相似特征［9］。与单测点相比，监控变形规律相似的测点群更能如实反映结构的运行状态。一些学者依据面板数据理论，考虑群体变形相似特征，建立了HST 面板模型［10-11］，尽管取得了一定进展，但仍存在如下不足：①将测点群内个体变形统一解释为水压、温变和时效分量，未刻画边界约束等因素的影响，这些因素对个体变形的作用效应存在一定差异，难以理论表征；②与HST 配套使用的置信区间准则［7，12］依据典型小概率原理建立，仅可辨识出单测点的异常变形。

针对上述问题，笔者以变形规律相似的测点群为监控对象，将固定效应和随机效应［13］引入到HST中，研究考虑个体差异效应的测点群变形分析模型构建方法。在此基础上，借助多元统计和典型小概率原理，将置信区间向多维置信椭球推广，探究测点群变形监控准则，并结合工程实例分析，检验该监控方法的性能。

1 监控方法

1.1 水压、温变和时效面板模型

假设某高拱坝的所有测点已被划分为若干个变形变化特征相似的测点群，记为G1，G2，…，Gp，…。设m为Gp中监测点的个数，x为Gp中某监测点，n为监测时长，t为监测日期，uGp为Gp的变形监测序列，ux为x的 监测序列，ut，x为x在日期t的监测值。依据面板数据格式［14-15］，uGp可表示为

1.1.1 水压面板模型

ux的水压 面板模型ûx，H可表 示为

依据式（2），建立uGp的水压面板模型ûGp，H，可表示为

其 中：aGp，H=[a1，Ha2，H…am，H]为 系 数 矩 阵；HGp=为m阶分块矩阵。

1.1.2 温变面板模型

ux的温变面板模型记作ûx，S，其表达式为

基于式（4），构建uGp的温变面板模型ûGp，S，可表示为

其 中：aGp，S=[a1，Sa2，S…am，S] 为 系 数 矩 阵；tGp=为m阶分块矩阵。

1.1.3 时效面板模型

ux的时效 面板模型ûx，T为

利用式（6），建立uGp的时效面板模型ûGp，T，其表达式为

其 中：aGp，T=[a1，Ta2，T…am，T]为 系 数 矩 阵；θGp=为m阶分块矩阵。

1.2 HST-FE/RE 面板模型

记aGp为uGp的 固定/随 机 效应，ax为ux的 固 定/随机效应，αt，x为ut，x的固定/随机效应，aGp表示为

HST-FE/RE 面板 模型ûGp可 表示为

若 对 于 任 意x=1，2，…，m，a1，x=a2，x=…=at，x=…=an，x均成立，则式（9）为固定效应构型；若对于任意x，y=1，2，…，m，ax和ay为相互独立的正态分布，且满足期望E(ax)=0，方差VAR(ax)=，则式（9）为随机效应构型。

本 研 究 利 用Hausman 检 验［13，16］决 策HST-FE/RE 构型，采用广义最小二乘法［17］确定待定系数矩阵aGp，H，aGp，S，aGp，T和aGp，应 用t检 验 评 价 因 子 重 要性，并使用复相关系数和剩余标准差评定模型精度。

1.3 置信椭球监控准则

记HST-FE/RE 面板模型对变形数据的拟合序列为，即

残差序列εGp可表示为

对于任意x，y=1，2，…，m，εx和εy服从一元正态分布且相互独立。依据多元统计理论［18-19］，εGp服从m元正态分布，其概率密度函数为

ωGp为均值矩阵，表示为

ΨGp为协方差矩阵，表示为

当显著性水平取α时，存在

置信水平α对应的概率密度函数值记为fα，则存在如下关系

将协方差矩阵ΨGp进行特征值分解，得到特征向量矩阵R与特征值矩阵Λ，即

R为正交矩阵，存在

可得

其中：rx为λx对应的特征向量。

将式（21）代入式（17）中，可得

式（22）的几何意义为m维概率空间中的置信椭球，球心为ωGp，半轴长为λx f α′，坐标方向为rx。

依据典型小概率原理，设置2 级置信水平α和β，其中α为正常和基本正常的临界状态，β为基本正常和异常的临界状态，则置信椭球监控准则可表示为

本研究算法流程如图1 所示。

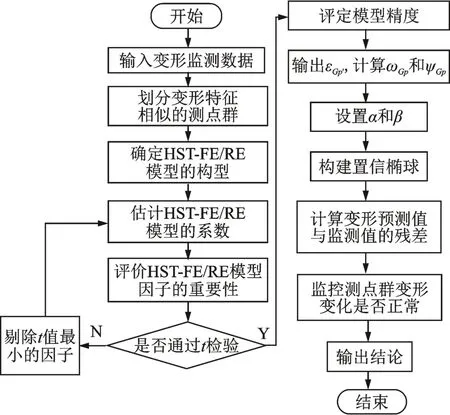
图1 算法流程Fig.1 Process of the proposed methodology

2 工程实例

甲高拱坝为混凝土双曲拱坝，坝顶高程为1 885.0 m，最低建基面高程为1 580.0 m，最大坝高为305.0 m，坝顶宽度为16.0 m，最大跨度为480.0 m，正常蓄水位为1 880.0 m，死水位为1 800.0 m。图2 为甲高拱坝垂线监测点布置图，32 个垂线监测点布置在5#，9#，11#，13#，16# 和19# 坝 段，编 号 为No.1~No.32。

图2 甲高拱坝垂线监测点Fig.2 Observation points of the investigated high arch dam

2.1 变形规律相似的测点群划分

2014-01-01 至2015-06-30，32 个 测 点 的 径 向变形及上游水位过程线如图3 所示，利用文献［9］的方法划分变形特征相似的测点群。该方法采用综合距离衡量变形相似程度，并自下而上划分测点群，32 个测点的分群过程如图4 所示。综合距离与合并次数的关系如图5 所示。由图4，5 可知，经过31 次合并，所有测点成为1 个群。在第30 次合并时，综合距离发生突变，变形规律差异较大的2 个测点群被合并。因此，32 个测点被划分为3 个变形相似的测点群，即Ⅰ，Ⅱ，Ⅲ群。变形规律相似的测点群如图6 所示，由图可知：Ⅰ群大致在拱坝上部；Ⅱ群分布在拱坝中部；Ⅲ群位于靠近坝基与近岸山体的部位。不同测点群的径向变形对比如图7 所示，Ⅰ群测点的径向变形如图8 所示，可以看出：同群测点的变形量级及变化规律相似，如PL5-1 和PL5-2；而异群测点的变形特征差异较大，如PL5-1和PL13-5。

图3 径向变形及上游水位过程线Fig.3 Time series of radial deformation and upstream water level

图4 32 个测点的分群过程Fig.4 Grouping process of the 32 observation points

图5 综合距离与合并次数的关系Fig.5 Relationship between the comprehensive distance and combination time

图6 变形规律相似的测点群Fig.6 Observation point groups with similar deformation behaviors

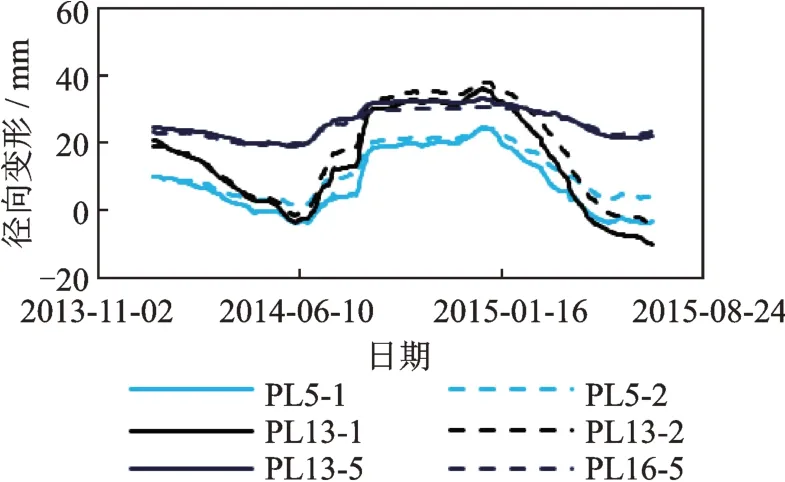
图7 不同测点群的径向变形对比Fig.7 Comparison of radial deformation among observation point groups

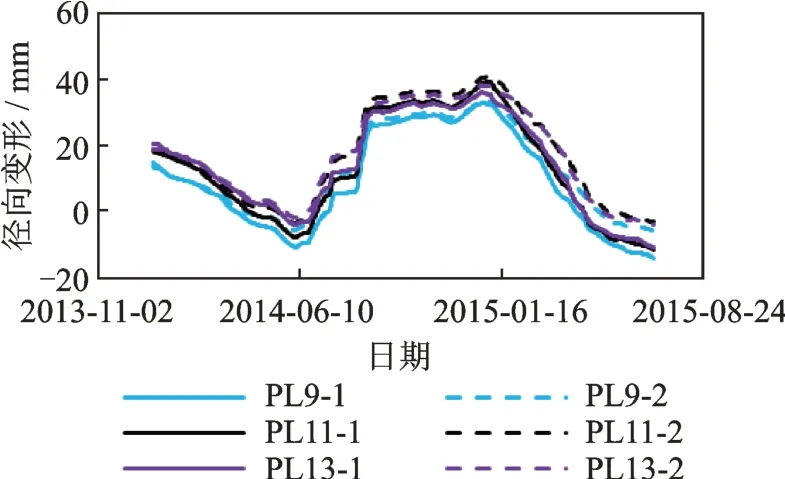
图8 Ⅰ群测点的径向变形Fig.8 Time series of radial deformation of Group Ⅰ

2.2 Ⅰ测点群变形监控

利用Ⅰ群测点（PL9-1，PL9-2，PL11-1，PL11-2，PL13-1 及PL13-2）的 径 向 变 形（图8）和 库 水 位（图3）监测资料，建立HST-FE/RE 面板模型。应用STATA 软件进行Hausman 检验，结果显示，原假设被拒绝，选用固定效应构型。HST-FE/RE 模型系数如表1 所示，Ⅰ群变形监测值、拟合值和残差如图9 所示，可知复相关系数为99.875%，剩余标准差为0.016 34，拟合精度较高。HST-FE/RE 模型变形最大变幅中各分量占比如表2 所示，可知最主要的影响因素为水压，其次为温变，最后为时效和固定效应。

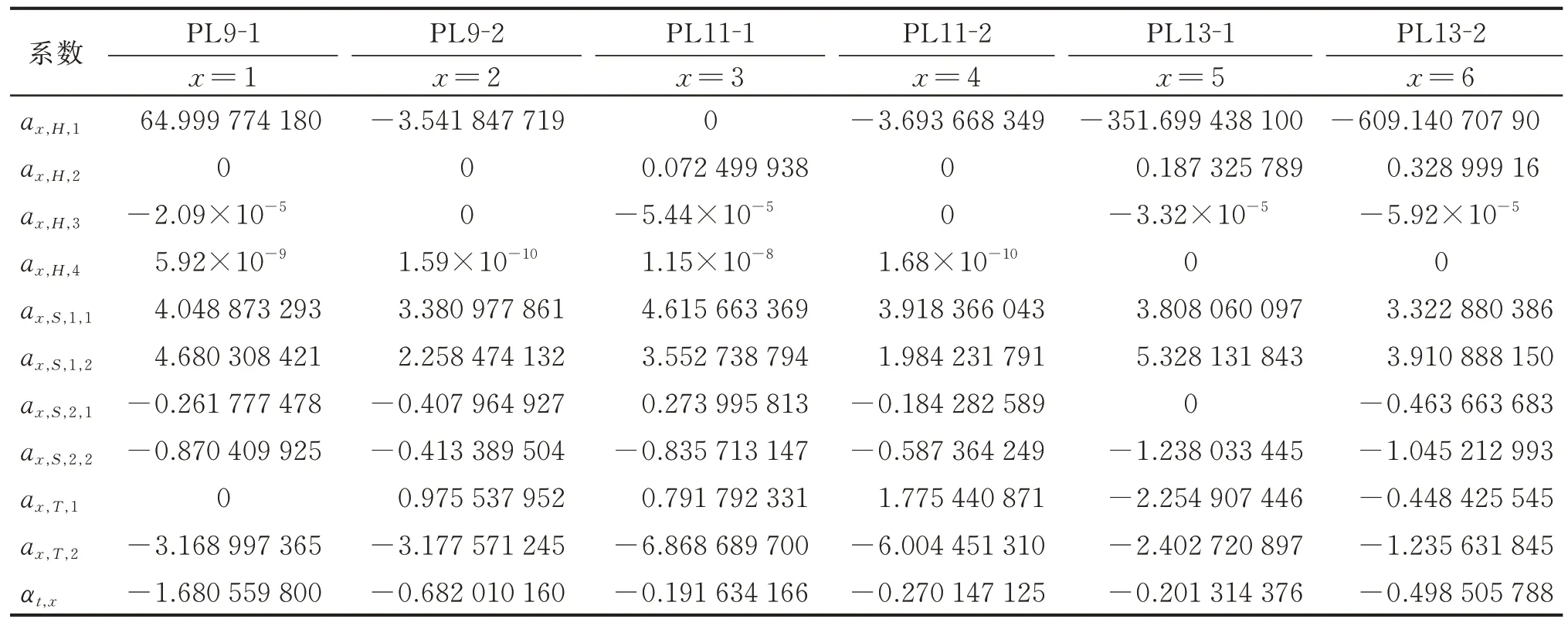
表1 HST-FE/RE 模型系数Tab.1 Coefficients of the HST-FE/RE model

表2 HST-FE/RE 模型变形最大变幅中各分量占比Tab.2 Component proportions of maximum amplitude of the HST-FE/RE model

图9 Ⅰ群变形监测值、拟合值和残差Fig.9 Deformation monitoring values, fitting values and residuals of Group Ⅰ

为检验HST-FE/RE 面板模型的性能，与文献［7］中的HST 模型进行对比分析。图10 为HST 和HST-FE/RE 的变形预测值，经计算，HST 模型的复相关系数为94.125%，剩余标准差为0.053 14，HST-FE/RE 的拟合精度高于HST。图11 为HST和HST-FE/RE 的变形预测相对误差，分别利用HST-FE/RE 和HST 预 测PL9-1 测 点2015-07-01 至2015-07-31 的径向变形，最大相对误差分别为3.28%和12.69%，且HST-FE/RE 的相对误差过程线更平稳。与HST 相比，HST-FE/RE 的预测性能更佳。

图10 HST 和HST-FE/RE 的变形预测值Fig.10 Deformation prediction results of the HST and HSTFE/RE

图11 HST 和HST-FE/RE 变形预测相对误差Fig.11 Deformation prediction relative errors of the HST and HST-FE/RE

依据HST-FE/RE 建模结果，输出矩阵εGp，计算矩阵ΨGp和ωGp，分别将α和β设置为0.05 和0.01，可在6 维概率空间中构建2 个置信椭球，置信椭球在坐标面上的投影如图12 所示，其中：实线为正常和基本正常的临界状态；虚线为基本正常和异常的临界状态。依据置信椭球准则，监控Ⅰ群测点2015-07-01 至2015-07-31 的径向变形变化处于正常范围内，其径向变形监控如图13 所示。

图12 置信椭球在坐标面上的投影Fig.12 The projections of confidence ellipsoids on coordinate planes

图13 2015-07-01 至2015-07-30 径向变形监控Fig.13 Radial deformation monitoring from 2015-07-01 to 2015-07-30

2.3 讨 论

1） 在监控测点群变形变化时，仅用水压、温变和时效3 个常规分量难以对模型进行解释。由于考虑了个体差异效应，HST-FE/RE 的性能优于HST。本研究建立的HST-FE/RE 面板模型适用于分析高拱坝短期变形变化，对于长期变形可以采用分段建模的方式解决。

2） 置信椭球准则是置信区间准则在多维概率空间中的推广，相较于置信区间准则，置信椭球准则对典型小概率变形的辨识更为严格。若测点群变形状态发生变化，例如：正常→基本正常或基本正常→异常，则表明高拱坝变形群体相似特征发生了不同程度的改变。

3 结 论

1） 布置于高拱坝的测点可划分为若干个变形规律相似的群体，在刻画测点群变形变化时，仅采用水压、温变和时效分量是不够的，需将测点群变形的个体差异效应考虑在内。

2） 在建立水压、温变和时效面板模型的基础上，引入FE 和RE 表征个体差异效应，据此提出了HST-FE/RE 面板模型。综合应用多元统计理论和典型小概率原理，建立了置信椭球准则，实现了测点群变形变化同步监控。

3） 工程实例分析显示：HST-FE/RE 和HST 变形拟合复相关系数分别为99.875%和94.125%，剩余标准差分别为0.016 34 和0.053 14，HST-FE/RE的拟合精度比HST 高；HST-FE/RE 的相对误差波动比HST 更为平稳，最大值分别为3.28% 和12.69%，预测性能优于HST；作为置信区间准则在多维概率空间中的推广，置信椭球准则对典型小概率变形的辨识更为严格。因此，将HST-FE/RE 和置信椭球准则相结合监控高拱坝变形变化是可行的，其性能优于常规方法。