基于CE/SE方法的某大口径火炮模块装药内弹道数值模拟

冯渊，王育维，朱文芳，赵娜，刘琦

(西北机电工程研究所，陕西 咸阳 712099)

模块装药的优势在于能够与火炮自动装填技术相匹配从而极大程度上提升火炮射速,有利于简化装药种类、方便后勤管理[1],且可以通过不同模块药的组合实现火炮的不同弹丸初速和射程[2]。无论是在国际上还是在国内,大口径火炮武器逐渐趋向于采用模块装药技术。当前,世界主要军事强国,包括美国、德国、以色列、南非等,都对模块装药技术以及应用开展了较为深入的研究,相关技术、研究成果和应用方面正在走向成熟。我国也在开展模块装药技术的相关研究工作,探索模块装药技术在多种口径火炮中的应用。目前,模块装药的相关研究中,仍有一些技术问题有待解决,例如小号装药燃尽性问题,可燃容器与发射药燃烧匹配性问题等[2]。

上世纪末以来,随着计算机技术的快速发展,数值模拟方法已逐渐成为火炮发射内弹道、装药结构设计以及模块装药等研究的重要方法。尤其是多相流理论应用于内弹道模拟计算领域后,发展出了多维两相流内弹道理论体系,不仅能够模拟弹丸运动特性以及膛压变化趋势,而且能够对压力波动现象进行模拟,进而对内弹道环境安全性进行评价。近年来,研究人员采用数值模拟的方法,对各个种类和口径火炮发射内弹道问题[3-5],包括采用模块装药的大口径火炮发射内弹道问题[1, 6-7],进行了深入研究,不断完善了数学模型,并获得重要结论,对内弹道和装药设计的研究起到了指导作用。

在现有的火炮两相流内弹道模拟研究中,应用最为广泛的是MacCormack格式。时-空守恒元与求解元方法(即CE/SE方法)是基于空间通量与时间通量的守恒性原理推导出来的,与MacCormack格式等传统计算方法有很大区别[8]。CE/SE方法能够在空间和时间上都保持二阶精度,对激波等强间断性具有很高的分辨率。应用于对内弹道问题进行模拟时,无需在数学模型中添加人工粘性项[8]。早期,CE/SE方法以其捕获间断能力强的优点,主要被应用于对爆轰波的模拟研究[9-12]。近期,南京理工大学研究人员已将CE/SE方法从气相流拓展到气固两相流,并对点传火管内两相流动过程[13-14]以及火炮发射内弹道过程[8,15]进行了模拟研究,证明了CE/SE方法模拟内弹道两相流问题的可行性。

笔者进一步将CE/SE方法进行拓展,在两相流内弹道数学模型中考虑可燃容器对内弹道过程的影响,构造出基于CE/SE方法的模块装药(含可燃容器)两相流内弹道数学模型,并应用该模型对采用模块装药的某大口径火炮发射内弹道过程进行了模拟,验证了该模型应用于模拟模块装药两相流内弹道问题的正确性。此外,笔者还研究了可燃容器能量、装药长等参数对内弹道环境的影响。

1 数学模型

1.1 模块装药一维两相流内弹道数学模型

大口径火炮膛内模块装药装填结构示意图如图1所示,即笔者模拟工作所依据的物理模型。

根据大口径火炮发射模块装药的内弹道特点,将膛内区域分为主装药区域和中心点传火管区域两个部分。同时,为了建立模块装药一维两相流内弹道数学模型,需要进行如下的基本假设:

1)燃烧产物组分保持不变,火药燃气的热力学参数为常数。

2)中心点传火管采用等截面的一维两相流偏微分方程组描述,且通过气相质量、动量和能量源项与药室内主装药区域守恒方程耦合;中心点传火管内的固相不会进入主装药区。

3)由发射药颗粒群组成的固相连续地分布在气相中,并把发射药颗粒群当作一种具有连续介质特性的拟流体来处理。

4)用发射药表面的温度代表整个发射药颗粒的温度(即药温),且认为药温达到着火温度后即被点燃。

5)认为发射药粒是不可压缩的,计算流动参数时忽略发射药的实际形状,以发射药粒当量球半径代替药粒几何尺寸。

6)假定发射药及可燃容器燃烧仅与压力相关,且发射药燃烧服从几何燃烧定律和指数燃烧规律,可燃容器燃烧服从渗透性燃烧规律。

7)发射药及可燃容器的燃气服从诺贝尔-阿贝尔状态方程。

8)在主装药区,忽略中心点传火管占据的体积。

9)将炮膛形状简化为圆柱,即假设图1中药室和身管的内径相同。

笔者仅对主装药区域的一维两相流数学模型进行介绍,中心点传火管区域的一维两相流数学模型与主装药区域十分相似。气相质量和动量方程、能量方程以及固相(发射药)质量和动量方程如式(1)～(5)所示,可燃容器的质量方程如式(6)所示。

(1)

(2)

(3)

(4)

(5)

(6)

以上数学模型中:ug和up分别为气相速度和固相速度;F1为中心点传火管的截面积;F为药室截面积;ρp和ρp2分别为火药和可燃药筒的密度;φ、σ和σ2分别为空隙率、火药持料率和可燃药筒持料率,显然φ+σ+σ2=1;fs为相间阻力;Rp为颗粒间应力;Hg、Hp和Hp2分别为火药燃气的比焓、单位质量的火药所含总能量以及单位质量的可燃药筒所含总能量;Q是相间换热量。这些参数的计算可参考相关著作或文献[16-17]。

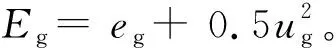
(7)

式中:R为气体常数;γ为比热比。

p、ρ和T分别为火药燃气的压力、密度和温度,根据假设,它们之间满足诺贝尔-阿贝尔状态方程:

(8)

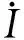
(9)

(10)

(11)

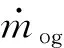
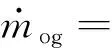
(12)

1.2 发射药与可燃药筒燃烧模型

需要注意的是,式(9)～(10)中,可燃药筒相对燃烧体积ψ2、单个发射药颗粒的表面积Sp和质量Mp的计算都需要结合发射药及可燃药筒的燃烧情况进行计算,因此有必要引入相应的燃烧模型。

在内弹道数值模拟中,通常引入相对已燃厚度z和相对已燃体积ψ来描述火药的燃烧情况,其定义分别如下:

z=e/e1,

(13)

ψ=1-Vp/V0,

(14)

式中:e1为火药的半弧厚;e为火药已燃厚度;Vp为火药颗粒的体积;V0为火药颗粒的初始体积。相对已燃厚度和相对已燃体积满足关系:

(15)

式中,χ、λ、μ、χs和λs均为火药的形状系数,由火药的种类和具体尺寸参数决定。

在内弹道过程中,火药相对已燃厚度z的演化满足:

(16)

对于可燃药筒采用渗透性燃烧规律,其相对已燃体积ψ2的演化满足:

(17)

将式(16)～(17)进行迭代求解,便得到每一时刻发射药颗粒和可燃药筒的燃烧情况,并在式(9)～(10)中求得相关变量,进而完成对模块装药一维两相流数学模型的求解。

1.3 CE/SE方法

1.3.1 无源项的CE/SE方法

笔者采用CE/SE方法对上述模块装药一维两相流数学模型的求解。模块装药一维两相流内弹道数学模型可写为矢量形式:

(18)

首先不考虑源项的影响,令式(18)中的源项T为0,则其可转换为

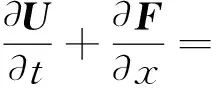
(19)

对时间和空间的统一处理,令x1=x,x2=t为欧式空间E2中的两个坐标,由高斯定理,方程(19)可以转换为

(20)

式中:S(V)为E2上任意时空区域的边界;h=(F,U),分别为时间-空间中气相、固相的质量、动量和能量的通量密度矢量。

在CE/SE方法中,对守恒元和求解元的定义是很重要的。将E2中网格点(j,n)的集合表示为Ω,其中n= 0, ±1/2, ±2/2, ±3/2,...;j=n±1/2,n±3/2,...,如图2所示。对每个网格点(j,n)∈Ω,取一个求解元SE(j,n)为图3中四边形ABCD。

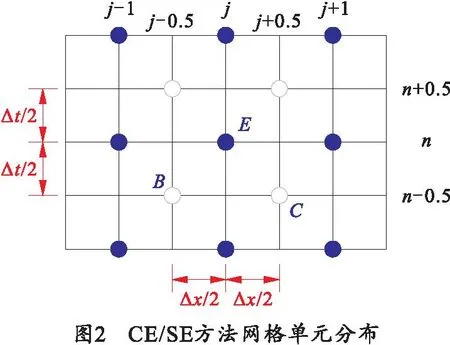
对于任意的(x,t)∈SE(j,n),U(x,t)和F(x,t)可用其相应的离散量U*(x,t;j,n)和F*(x,t;j,n)代替。利用一阶泰勒展开,对式(20)进行处理并将其在分别在图3中的AB、BG、GC、CD、DE和EA上取积分,并经过整理可得:

(21)

式(21)即为CE/SE方法的求解格式。在式(21)中,Ux可用如下方法计算:

(22)

式中,

(23)

由式(22)可以看出,在求解区域内每一网格点上的独立求解变量为2个,即U和Ux。F和Ft都可借助Jacobian矩阵求得。Jacobian矩阵定义为

(24)

于是,由式(19)可得:

(25)

1.3.2 源项的处理

2 模型验证

采用CE/SE方法,对某大口径火炮的发射内弹道过程进行了模拟,具体的计算参数如表1所示。其中,ω为装药量,Din为炮管直径,Vin为药室容积,Lg为弹丸行程长,m和φ分别为弹丸质量和次要功系数,m2为可燃容器质量。计算时设置时间步长为Δt=1 μs,初始时刻网格为均匀网格,其尺寸为Δx=25.4 mm。弹丸开始运动后,右边界采用动网格边界条件,并利用网格分裂技术,保证弹后第1个网格的尺寸始终在0.5Δx至1.5Δx之间。

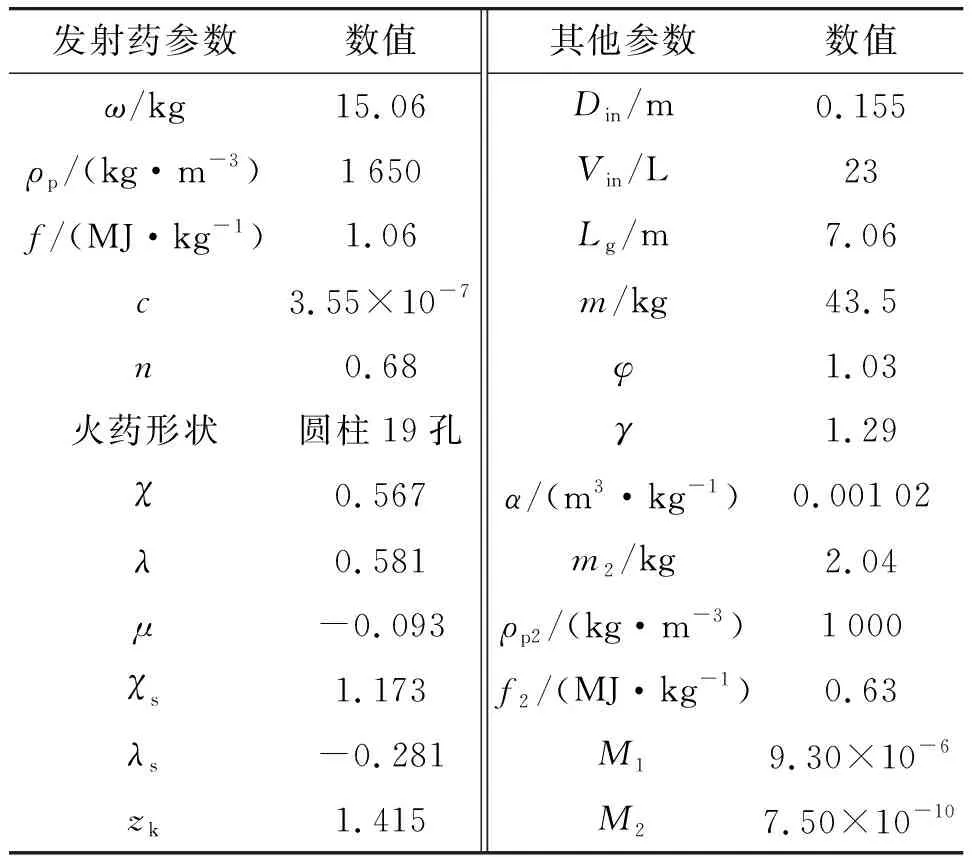
表1 计算参数列表

将模拟结果与采用相同火炮结构、弹丸、点传火系统以及装药参数等内弹道参数的某次试验结果进行对比,以验证笔者建立的模块装药一维两相流内弹道数学模型以及代码的正确性。模拟计算以及试验测试得到的膛压-时间曲线的对比如图4所示。由图4可见,在可燃容器以及发射药被点燃后,由于大量高压燃气的生成,膛内压力快速上升;当可燃容器先于发射药燃尽之后,虽然膛压仍然逐渐上升,但其上升速率有所下降。另一方面,当膛内压力超过弹丸启动压力时,弹丸开始在膛内高压燃气作用下做加速运动,弹后空间逐渐增大,这对膛压起到一个降低的作用。当弹后空间的增大对膛压的降低作用超过发射药燃烧生成燃气对膛压的上升作用时,膛压达到最大值后开始逐渐降低。

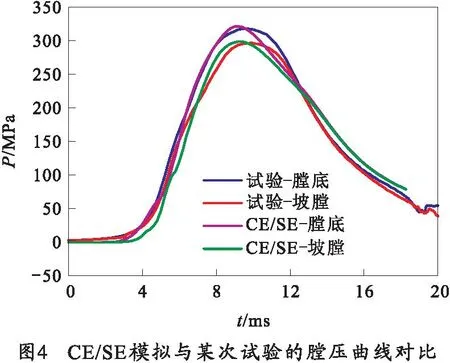
内弹道参数的试验测试结果与CE/SE方法模拟结果的对比如表2所示。由图4和表2可见,采用CE/SE方法模拟得到的膛压-时间曲线的变化趋势及最大膛压与初速等内弹道参数值均与试验测试结果吻合较好。膛底和坡膛最大压力以及弹丸初速,模拟结果与试验测试结果的相对偏差分别为0.25%,0.07%和0.50%。对比结果表明笔者建立的基于CE/SE方法模块装药一维两相流内弹道数学模型能够准确地对火炮发射内弹道过程进行模拟,进而准确地获得关键内弹道参数,为内弹道和装药设计提供有效的途径。

表2 试验测试与CE/SE方法模拟的对比

3 结果与讨论

3.1 CE/SE方法模拟内弹道相关参数的轴向分布

图5～7分别给出了火炮射击内弹道过程中不同时刻膛内压力、气相速度和空隙率的轴向分布。

由图5～7可见,在t=4 ms时刻,弹丸尚未运动,由于中心点传火管靠近膛底的位置率先破孔和破碎,导致膛底处发射药和可燃容器被点燃的时间较早,因此膛底处压力高于弹底处。在轴向压力梯度作用下,气相速度始终大于0,且呈两边低中间高的趋势,膛底和弹底处气相速度为0。

在t=5 ms时刻,膛内压力已经高于弹丸启动压力,弹丸开始运动,但运动速度较低。整个火药床也在向弹底逐渐运动,造成弹底周围火药堆积,因此弹底处空隙率明显低于膛内其他区域。由于此时弹底处的火药颗粒尚未开始燃烧,因此弹底处火药颗粒的堆积并未引起压力波动。

在t=6 ms时刻,气相速度的分布呈三角函数的形状,在靠近弹底位置处气相速度大于0,而在靠近膛底位置处气相速度小于0。事实上,此时固相速度的分布也有这一规律。于是,由于弹丸的运动,弹后空间增大,而药温较低,燃气生成速率很低,同时受气相和固相速度分布的影响,其他位置处的气相和固相均无法及时补充到弹后空间,因此弹后空间高温燃气发生膨胀,弹底压力明显低于其他位置膛压,且空隙率呈现出先降低而后在弹底处突然升高的特点。

在t=7～13 ms时刻,随着膛内压力的逐渐升高,弹丸运动速度显著加快;膛内压力的分布始终呈现逐渐降低的趋势,即膛内始终存在沿着轴向的压力梯度;空隙的分布呈逐渐上升的趋势,这是由于弹后空间的逐渐增大导致的;气相速度的分布呈现出线性上升的趋势。

在t=14 ms时刻以及之后,由于发射药逐渐燃尽,在图7中不同位置处的空隙率均逐渐趋向于1;膛压逐渐降低,其分布仍然呈现逐渐降低的趋势,但膛底和弹底的压差逐渐减小,即压力分布逐渐趋向于拉格朗日假设分布;气相速度分布仍然呈线性增大的趋势,虽然弹丸运动速度逐渐增大,但由于膛压的降低,速度梯度在逐渐减小。

此外,由图5～7可见,笔者建立的基于CE/SE方法的模块装药一维两相流内弹道数学模型不仅能够准确描述膛压等内弹道参数随时间的变化规律,还能够模拟出各内弹道参数的空间分布情况,为内弹道和装药设计以及内弹道环境的改善提供理论依据。

3.2 可燃容器能量对内弹道环境的影响

可燃容器本身也是一种含能材料,其燃烧将会产生高温高压的燃气。可燃容器与发射药之间的燃烧匹配性能是模块装药的关键技术之一[2]。一方面,要保证可燃容器内弹道过程期间需要完全燃尽,不影响下一次射击的弹药装填;另一方面,要避免可燃容器的燃烧在膛内造成压力波动现象而改变内弹道环境。可燃容器的燃烧性能受多方面因素的影响,包括可燃容器的能量、燃烧特性、工艺性能、结构等。现有的研究结果表明,可燃容器的能量对可燃容器燃烧性能的影响最大。可燃容器的能量越高,体现为可燃容器的燃速快、能量越大。笔者在基于CE/SE方法的模块装药一维两相流内弹道数学模型的基础上,采用可燃容器特有的渗透性燃烧规律控制方程式(17),通过改变可燃容器燃烧系数M1和可燃容器火药力f2的方式来实现模拟可燃容器能量变化造成的影响,模拟研究了可燃容器能量对某大口径火炮发射内弹道环境的影响。

不同可燃容器的燃烧系数M1和火药力f2取值如表3所示,不同可燃容器能量条件下模拟获得的压力-时间图线如图8所示,此外,表3还给出了通过模拟计算获得的可燃容器能量对内弹道参数的影响。

表3 可燃容器能量对内弹道参数的影响

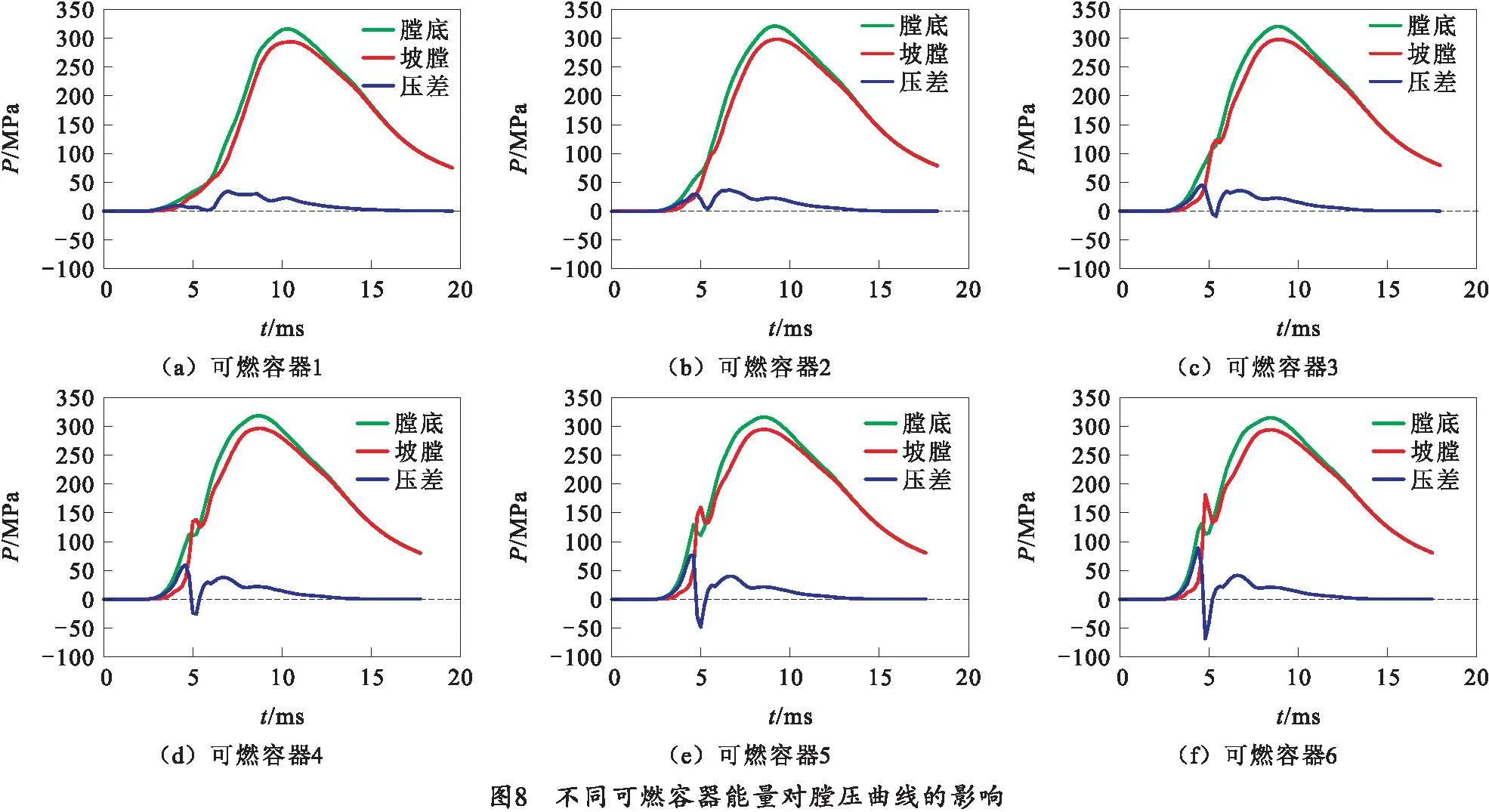
由表3和图8可以看出,对于能量最低的可燃容器1,膛底和坡膛处压力曲线的斜率最小,在内弹道初期,膛底和坡膛处压力非常接近;当弹丸开始运动后,膛内逐渐形成10～30 MPa的压力梯度;当达到最大膛压点之后,膛底和坡膛的压差又逐渐减小,直到最终压差几乎为0。此外,在整个内弹道过程中,膛底处压力始终高于坡膛压力,未产生与弹丸运动方向相反的压力梯度;可燃容器的燃烧也未使膛底和坡膛处形成压力初峰,膛压曲线较为光滑。

对于可燃容器2,由于其火药力以及燃速明显大于可燃药筒1,因此在内弹道初期膛压曲线斜率较高,可燃容器燃尽的时间也提前。在整个内弹道过程中,膛底与坡膛的压差始终大于0,表明未产生与弹丸运动方向相反的压力梯度。此外,与图8(a)相同,可燃容器2的燃烧也未在膛底和坡膛处形成压力初峰,膛压曲线仍然较为光滑,压力波动现象不明显。

对于可燃容器3,由于其火药力以及燃速的进一步增大,相比于可燃容器1～2,其内弹道初期膛压曲线斜率进一步增大,尤其是在坡膛处,在5.2 ms时刻坡膛压力高于膛底压力,形成与弹丸运动方向相反的压力梯度,最大负压差为-9.11 MPa。在整个内弹道过程中,膛压曲线仍然较为光滑;可燃容器3的燃烧未在膛底形成压力初峰,但在坡膛处形成了轻度压力双峰现象,压力初峰为122.8 MPa。

对于可燃容器4～6,相比于可燃容器3,压力波动现象更加严重。在内弹道初期,由于能量较高,可燃容器的燃烧使膛底和坡膛处均产生较为明显的压力双峰现象,且坡膛处压力初峰值略高于膛底处压力初峰值,膛压曲线不再光滑;这是由于发射药向弹丸底部运动并引起堆积的同时剧烈燃烧产生大量高压燃气导致的。此外,由表3和图8可见,可燃容器能量越高,可燃容器燃烧形成的膛底和坡膛的压力初峰值越高,压力波动现象越明显,最大负压差也逐渐升高。此外,对于可燃容器4～6,总体呈现随着可燃容器能量增加,弹道环境向变坏方向发展。

综上所述,随着可燃容器能量的增大,膛内压力波动现象变得更加明显,逐渐形成与弹丸运动方向相反的压力梯度,且最大负压差逐渐增大;膛压曲线也逐渐由光滑变为畸形,在膛底和坡膛处均形成压力双峰现象,且压力初峰值也逐渐增大。此外,由表3中的数据可见,除了可燃容器1的弹丸初速明显低于其他工况外,可燃容器的能量对最大膛压和弹丸初速的影响不明显。

以上结果表明,在模块装药设计中,必须考虑可燃容器的能量对压力波动的影响,保证可燃容器与发射药的燃速相匹配,才能在提高弹丸初速的同时,弱化膛内压力波动现象,提高发射安全性。

3.3 装药长度对内弹道环境的影响

装药长度也是影响火炮发射内弹道环境的一个重要因素。早期的研究者就已经发现,即使在使用低装填密度、低性能的火炮武器时,小号装药也可能会引起压力波动甚至膛炸现象[16],因此规定装药长度一般不能短于药室长的2/3。

通过笔者建立的基于CE/SE方法的模块装药一维两相流内弹道数学模型,对不同装药长度条件下某大口径火炮发射内弹道过程进行模拟,定量对比和分析了装药长度对火炮发射内弹道环境以及压力波动现象的影响,进一步对建立的基于CE/SE方法的模块装药一维两相流内弹道数学模型进行了验证。在这一部分的模拟中,计算参数的取值仍如表1中所示,换而言之,这一部分模拟的模块装药仍为全装药,只有装药长度发生改变。不同装药长度条件下的膛压-时间曲线如图9所示。如图9(a)～(c)所示,当装药长度/药室长不低于0.921时,膛底和坡膛处的压力-时间曲线均较为光滑,内弹道初期并未出现压力初峰现象,且膛底压力始终高于坡膛压力,即未产生与弹丸运动方向相反的压力梯度,内弹道环境较为良好。如图9(d)所示,当装药长度/药室长为0.882时,膛底和坡膛处的压力-时间曲线变得不再光滑,在t=5 ms时刻之后,膛底和坡膛处先后分别出现了67.4 MPa和100.2 MPa的压力初峰;此外,在t=5.4 ms时刻,出现了-22.1 MPa的负压差,表明随着装药长度的减小,内弹道环境开始恶化。当装药长度/药室长下降至0.866和0.843时,内弹道环境进一步恶化;如图9(e)所示,膛底和坡膛处的压力初峰值分别为70.1 MPa和108.1 MPa,最大负压差为-48.6 MPa;如图8(f)所示,膛底和坡膛处的压力初峰值分别为了76.0 MPa和144.8 MPa,最大负压差达到了-94.3 MPa。

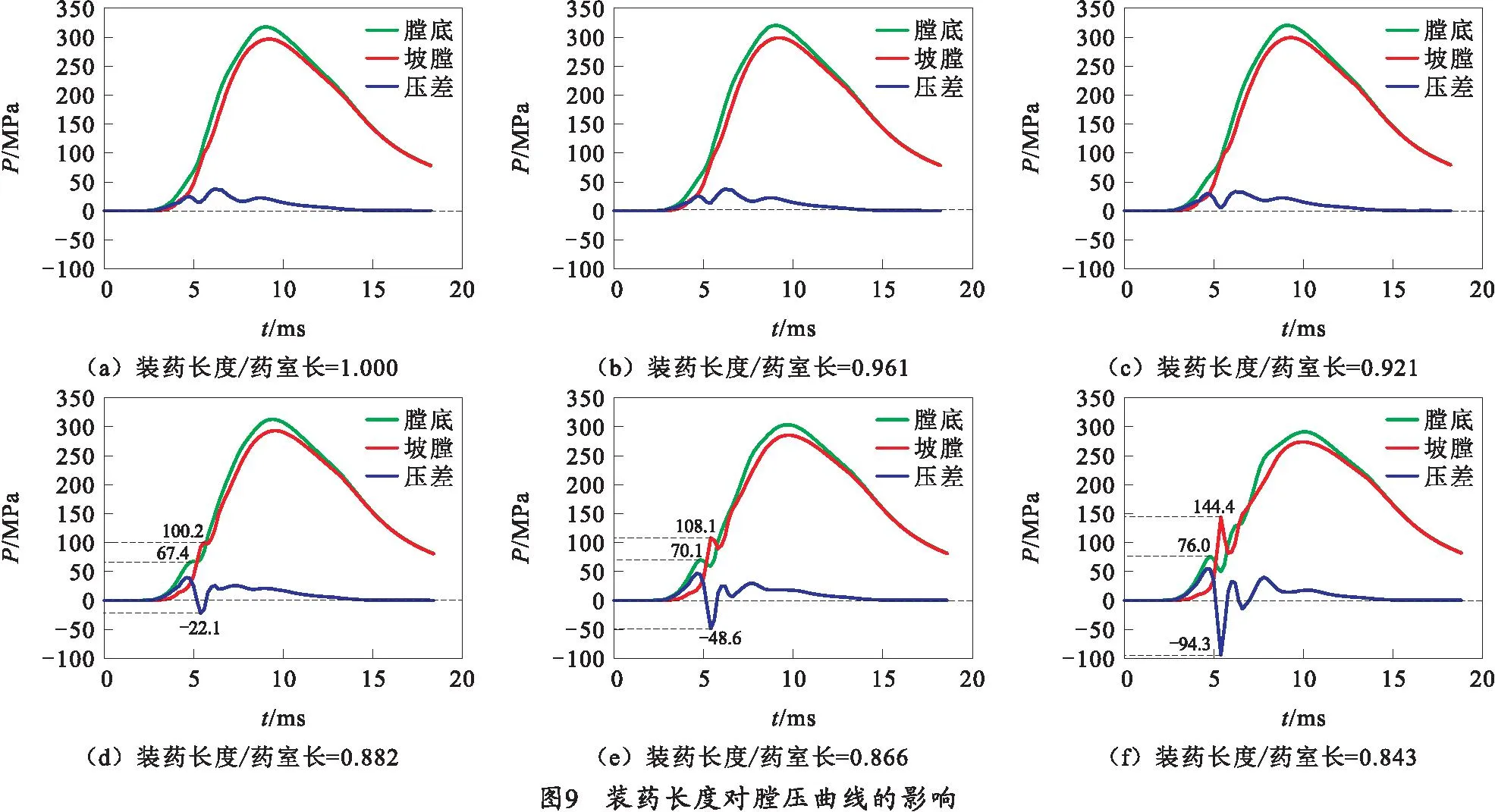
模拟结果表明,随着装药长度的减小,由于装药结构的不均匀度逐渐增大,压力波动现象越来越显著。当装药长度下降至某一特定值后,压力曲线开始不再光滑,而是出现压力初峰的现象,并开始出现负压差,同时,压力初峰值以及负压差值均随装药长度减小而显著增大。

4 结论

笔者建立了基于CE/SE方法的模块装药一维两相流内弹道数学模型,并应用该模型对采用模块装药的某大口径火炮发射时的内弹道过程进行了数值模拟。通过将模拟结果与某次试验结果进行对比,证明了笔者建立的数学模型能够正确模拟出给定装药、弹丸、可燃容器和火炮结构参数条件下的膛压曲线,获得准确的最大膛压和弹丸初速等内弹道参数,与实验值的相对偏差在1%左右。此外,基于模拟结果,分析研究了可燃容器能量以及装药长度对内弹道参数和压力波动现象的影响。结果表明:

1)随着可燃容器能量的增大,膛内压力波动现象越明显,逐渐形成与弹丸运动方向相反的压力梯度,膛底和坡膛处逐渐产生压力双峰现象。最大负压差以及膛底、坡膛的压力初峰值随着可燃容器能量参数的增大而逐渐升高。可燃容器能量达到一定程度后其再增加对最大膛压以及弹丸初速没有明显的影响。

2)随着装药长度的减小,由于装药轴向分布不均匀度逐渐增大,压力波动现象越来越显著。当装药长度下降至某一特定值后,压力曲线开始不再光滑,而是出现压力初峰的现象,并开始出现负压差,同时,压力初峰值以及负压差值均随装药长度减小的增大而显著增大。