基于时序分解和随机森林的时间序列多步预测算法

文家璇， 王 苗， 刘 济

（华东理工大学信息科学与工程学院, 上海 200237）

由于事物发展的影响因素不明确或者数据采集困难，许多预测问题演变为单变量时间序列预测问题，即从过去的时序数据中挖掘其自身内在的规律，从而对其未来发展趋势进行预测[1]。本文考虑此类单变量时间序列的多步预测问题，例如国际原油价格预测、维修备件需求预测、政府负债率预测、气象风速预测等。

时间序列预测模型有统计学预测模型、机器学习和深度学习预测模型、混合预测模型三大类。经典的统计学时间序列预测模型常见的有指数平滑法[2]、移动平均自回归[3]（Auto Regressive Integrated Moving Average，ARIMA）等，适用于线性和平稳的时间序列预测。机器学习和深度学习算法是最近几年被广泛使用的时间序列预测方法，如支持向量机[4]（Support Vector Machine，SVM）、长短期记忆神经网络[5]（Long Short-Term Memory，LSTM）、随机森林[6]（Random Forests，RF）等，具有模型构造灵活、适应性好、精度较高的优点。其中，RF 具有参数较少、泛化性能良好、实现较为简单等更为良好的特性，被许多学者青睐。Fiona 等[7]利用卫星收集的气象、植被等变量作为影响因子，建立了预测花粉浓度的RF 模型。Abul 等[8]利用RF 模型预测比特币和黄金价格的方向，结果表明RF 模型的精度高于常用的logit 模型。RF 是一种集成学习算法，它构造若干性能不同的基学习器，再通过一定的策略进行集成，本文采用RF 算法建立时序分解后的各子序列预测模型。

基于模态分解的时间序列预测方法利用将复杂模态分解为较简单模态进行预测更为容易的思想，它属于混合预测模型的一种，目前有大量学者对此进行研究[5,9-13]。常见的时序分解方法有小波分解（Wavelet Transform，WT）、经验模态分解（Empirical Mode Decomposition，EMD）和变分模态分解（Variational Modal Decomposition，VMD）等。VMD 方法由Dragomiretskiy 等[12]提出，可有效避免EMD 方法存在的模态混叠现象，并具有良好的噪声鲁棒性，被广泛应用于时间序列预测研究中。Zhang 等[9]将VMD 和粒子群算法优化的支持向量机回归结合，建立了短期电力负荷预测模型，并得到了精度较高的结果。Li 等[10]则是利用VMD 将原始负荷数据分解为不同的子模态，然后使用基于蚱蜢算法的最小二乘支持向量机模型预测每个子模态的结果，求和得到最后的预测结果，与其他方案相比，该算法取得了最优结果。本文提出采用VMD 方法对复杂时间序列进行分解，从而建立预测模型。

目前，时序分解预测算法存在3 个方面的问题：（1）VMD 算法中分解子序列个数K和惩罚因子α的取值对结果影响很大，大多数研究使用人工经验取值，存在很大随机性[14]；（2）各子序列的模态特征各不相同，但现有研究仍然采用单一模型对不同子序列进行建模，没有利用各模态的相异性进行针对性的处理，导致部分子序列预测精度高、部分子序列的特征却没有充分挖掘[4-5,13-14]；（3）绝大多数文献的时序分解是对所有历史数据进行一次分解，再在各子序列划分训练集和测试集进行建模[14-16]，这种思路在建模阶段使用了测试集数据，实际应用时显然是不可行的。

针对上述问题，本文提出一种新的基于VMD 分解的时间序列预测方法，首先采用遗传算法对VMD 分解过程进行参数寻优，VMD 分解参数K和α随时间序列不同而自适应变化。其次，针对各子序列模态特征的不同，使用RF 构造若干差异显著的基学习器，对不同特征的子序列进行充分学习并建立较为准确的预测子模型。上述建模过程仅仅在原始数据的训练集上完成，实际测试（或应用）时，每产生一个新的已知数据，将其添加到历史数据末尾，重新进行VMD 分解和预测及重构，本文的这种实时分解预测思路能满足实际应用需要。

1 相关基础理论

1.1 VMD

VMD 是一种自适应非递归信号分解方法。它通过将输入信号x(t) 分解为一组离散的准正交带限模态子序列uk，将维纳滤波器推广到多个自适应频带，通过VMD 分解获得的模态主要分布在中心频率wk附近[17]。VMD 分解本质是一个变分优化问题，旨在最小化每种模态的带宽，可表示为：

其中：uk(t) 表示第k个子模态，k=1,···,K；wk表示其中心频率；x(t) 表示输入信号； δ (t) 表示狄拉克δ函数；∂t表示求时间梯度；j表示虚数单位； ⊗ 表示卷积运算符。

为了求解式(1)的优化问题，通常引入二次惩罚因子和拉格朗日乘子来处理约束，可以得到增广拉格朗日修正方程，

1.2 RF 算法

RF 算法是一种基于决策树和随机子空间理论的集成学习算法。其基本思想是构造若干性能不同的基学习器，并通过一定的策略组合基学习器的预测结果[18]。

其中：I(条件) 表示满足条件，返回值为1；不满足条件，返回值为0。

RF 这种随机子空间的集成学习策略，对于本文研究的问题有较大优势，由于使用VMD 分解得到的各个子序列具有显著差异性，单一结构的预测模型难以适用于每个子序列，导致部分子序列预测精度高、部分子序列的特征却没有充分挖掘。而RF 框架下，每个序列模型都是由基于自身样本和属性扰动获得的基学习器构成，有助于对不同特征的子序列进行充分学习并建立较为准确的预测模型。

2 VMD 的改进

由于VMD 的参数K和 α 对分解结果有较大的影响，本文引入排列熵(Permutation Entropy，PE)概念进行VMD 参数的优化，以获得最优分解参数K和 α 。Bandt 等[19]于2002 年提出排列熵作为衡量时间序列复杂度的一种指标，因为熵本身反映的就是一种有序的程度，熵越小说明越有序，因此可以将序列的排列熵值作为对分解后子序列容易预测程度的一种度量。

其中： P E(uk(n)) 为第k个子序列uk(n) 的排列熵值。将适应度函数的最小值作为寻优目标，以期望获得熵值最小、模态复杂度最低的子序列。

基于遗传算法的变分模态分解算法（GA-VMD）流程如图1 所示，对于每个参数K和 α 的个体，首先对原始时间序列进行VMD 分解，计算所得到的K个子序列的排列熵均值（PE 的计算可参考文献[18]）作为个体适应度，再进行遗传操作获得子代。该过程循环迭代，直到满足终止条件（大于最大代数Gmax）。

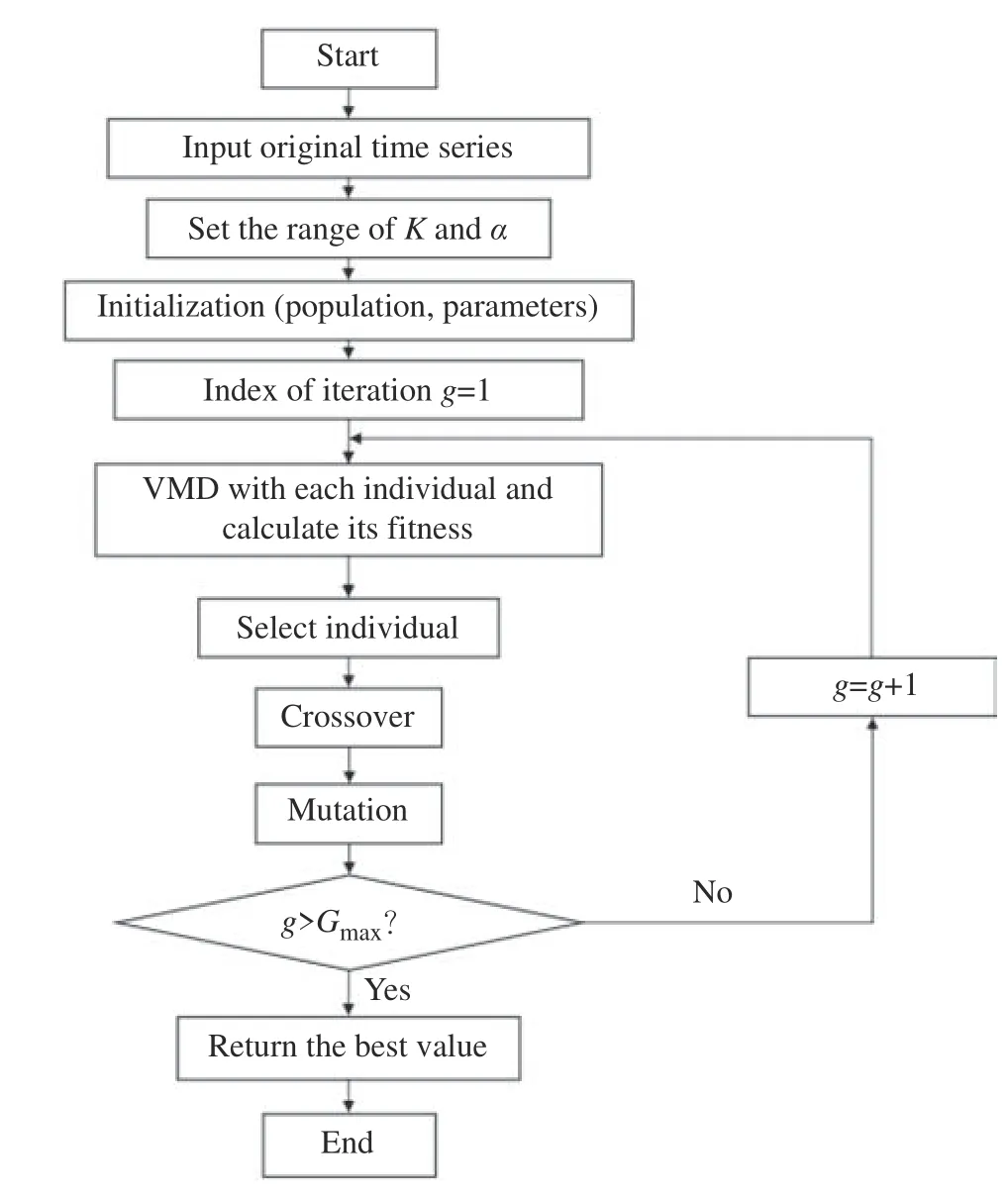
图1 基于遗传算法的变分模态分解算法（GA-VMD）流程Fig.1 Flow of variational modal decomposition based on Genetic Algorithm (GA-VMD)

3 基于GA-VMD 和RF 的预测算法

3.1 实时分解策略

从已有文献仿真研究可以发现，基于时间序列分解的预测建模往往是将全部时间序列数据进行一次分解，然后在每个子序列上划分训练集和测试集，用子序列训练集数据建立预测子模型，再用子序列测试集数据逐个输入预测子模型，检验模型的预测精度[14-16]。这种分解和建模策略存在不合理性，实际应用时测试数据是未知的待预测值，而一次分解策略将测试数据加入分解序列，分解过程已经预先学习了未来数据的特征，因此其最终预测精度很高，但实际上这样的模型是没有使用价值的。

本文针对一次分解策略存在的不合理和不实用问题，提出实时分解框架下的预测方法：对原始时间序列先行划分训练集和测试集，建模阶段只对训练集进行GA-VMD 分解，在每个子序列上训练预测子模型；预测阶段，每增加一个测试数据，将其添加到原始序列末尾，对新的序列进行GA-VMD 分解，再在每个子序列上用已建立的预测子模型进行实时预测。为了更清楚地对比一次分解和本文提出的实时分解策略，列出两种策略的伪代码如图2 所示。

图2 两种分解策略伪代码Fig.2 Pseudo code of two decomposition strategies

3.2 多步预测策略

时间序列多步预测常用的建模方法有迭代多步、多输出多步和多模型多步预测[20]等。图3 为3 种多步预测策略的对比图。其中，m表示输入序列长度，h表示预测步数，xn表示真实序列值， ︿xn+h表示预测值。

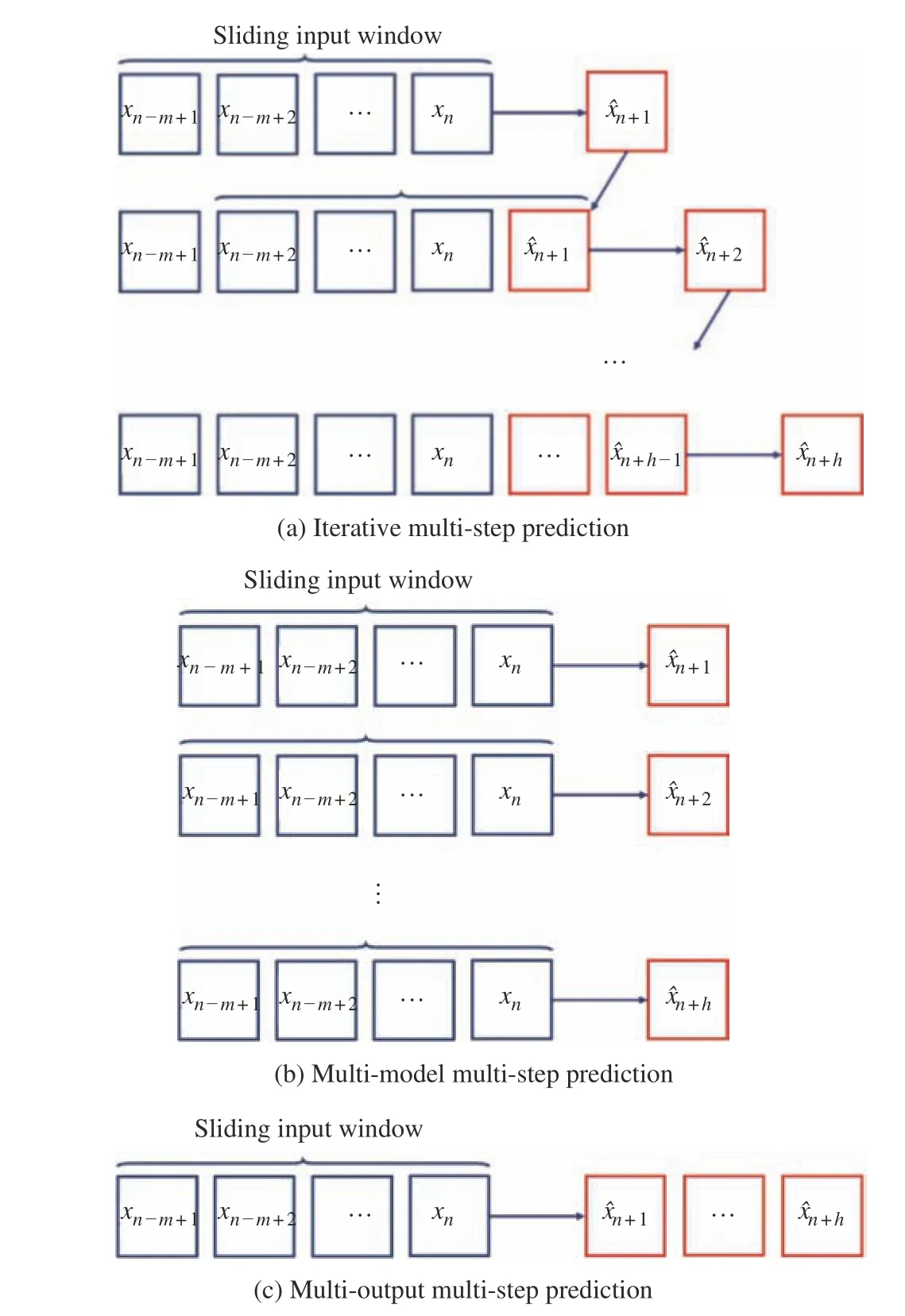
图3 多步预测策略对比Fig.3 Comparison of multi-step prediction strategies

迭代多步预测方法使用上一时刻的预测值来预测下一时刻的值，因此预测误差会累积，导致误差随预测步数增加急剧增大。多输出多步预测方法一次性预测多个时间步的值，预测模型的输出是多维的，模型结构简单，但训练出一个较为精确的模型存在较大困难。多模型多步预测方法对每个预测步分别建立预测模型，这样既可以避免迭代多步的误差累积，精度较高，又可以避免建立多输出精确模型的困难，但是建模代价较高，耗时较长。

本文将对比讨论3 种多步预测方法在基于时序分解的时间序列预测中的应用效果，以期得到一些一般性结论。

3.3 GA-VMD-RF 预测算法

综合前几节所述，基于实时分解、遗传算法优化的变分模态分解和多模型多步预测等策略，本文提出的GA-VMD- RF 预测算法流程如图4 所示。

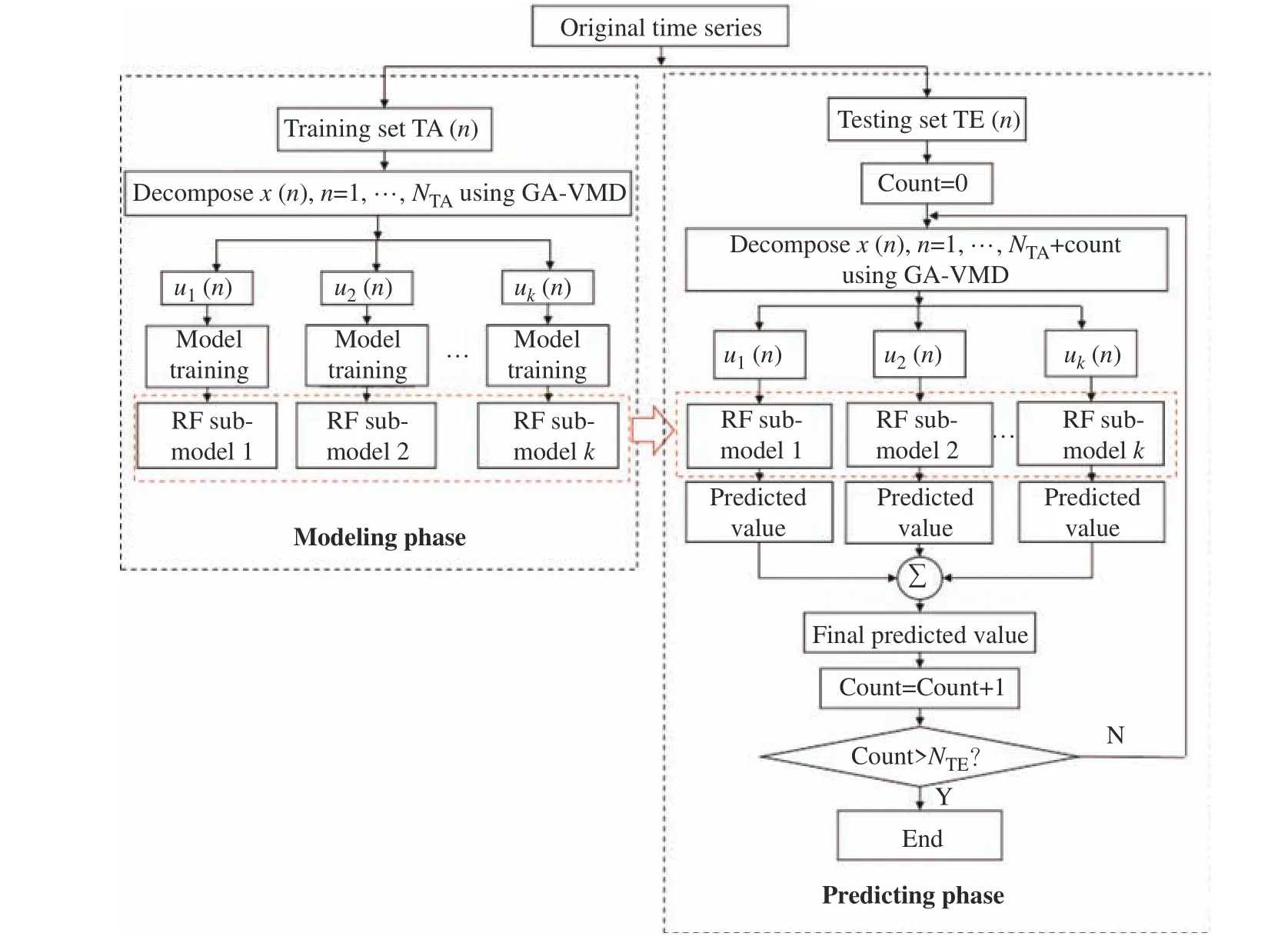
图4 VMD-GA-RF 预测算法流程图Fig.4 Flow chart of VMD-GA-RF algorithm

历史时间序列首先被划分为训练集 T A(n) 和测试集 T E(n) 。

（1）建模阶段。仅在训练集上（序列长度为NTA）进行GA-VMD 分解，得到K个最优子模态序列uk(n),k=1,···,K。利用RF 算法在每个子序列上进行预测模型训练，建立各RF 子模型k，所建立的RF 子模型将在预测阶段被使用。

（2）预测阶段。首先设置测试样本索引 count ，每获得测试集 TE(n) 的一个样本时，索引自动加1，分解时间序列长度也增加1。对已获得的所有时序数据（序列长度为NTA+count ）进行GA-VMD 分解，得到K个子序列uk(n),k=1,···,K。运用已建立的RF 子模型进行多步预测，然后重构求和各子模型的多步预测值，获得最终的多步预测结果。预测随时间递进，每次预测当前时刻下的多步预测值，当下一个时刻到来时，前一时刻的真实值将被添加到原始序列末尾，参与到下一个时刻的多步预测。

4 实验和分析

本文的实验数据来自于科罗拉多山脉的美国国家风速观测站[14]、UCI 数据网站和datahub 网站，数据 集1 为 美 联 储10 年 期（1953 年4 月 至2020 年1 月）美国政府债券的名义收益率的数据，数据集2 为欧洲布伦特原油价格自2017 年1 月1 日至2022 年6 月13 日的数据，数据集3 为科罗拉多山脉2022 年5 月10 日的风速数据，如图5 所示。

图5 数据集1～3Fig.5 Dataset 1—3

采用平均绝对误差(MAE)，平均百分比绝对误差(MAPE) 和均方根误差(RMSE) 对模型的预测结果进行评价，计算公式见式(7)：

将本文提出的算法与单一预测模型SVM、LSTM及时序分解预测模型VMD-RF、GA-VMD-LSTM 预测模型进行对比，并且，每种算法都同时测试了多模型多步预测（记为“MM”）、迭代多步预测（记为“IT”）、多输出多步预测（记为“MO”）。图6～8 所示为多模型多步预测策略下的预测曲线，图中灰色区域为真实值。可以看出，所提出的GA-VMD-RF 算法在一步、二步及三步预测点上预测精度较高，且相比于各对比算法总体表现更稳定。虽然GA-VMDLSTM 算法也具有相当的预测精度，但是它的性能不够稳定，在个别数据集如数据集2 上的预测精度不如GA-VMD-RF 算法。

图6 数据集1 预测结果Fig.6 Prediction result of dataset 1

图7 数据集2 预测结果Fig.7 Prediction result of dataset 2

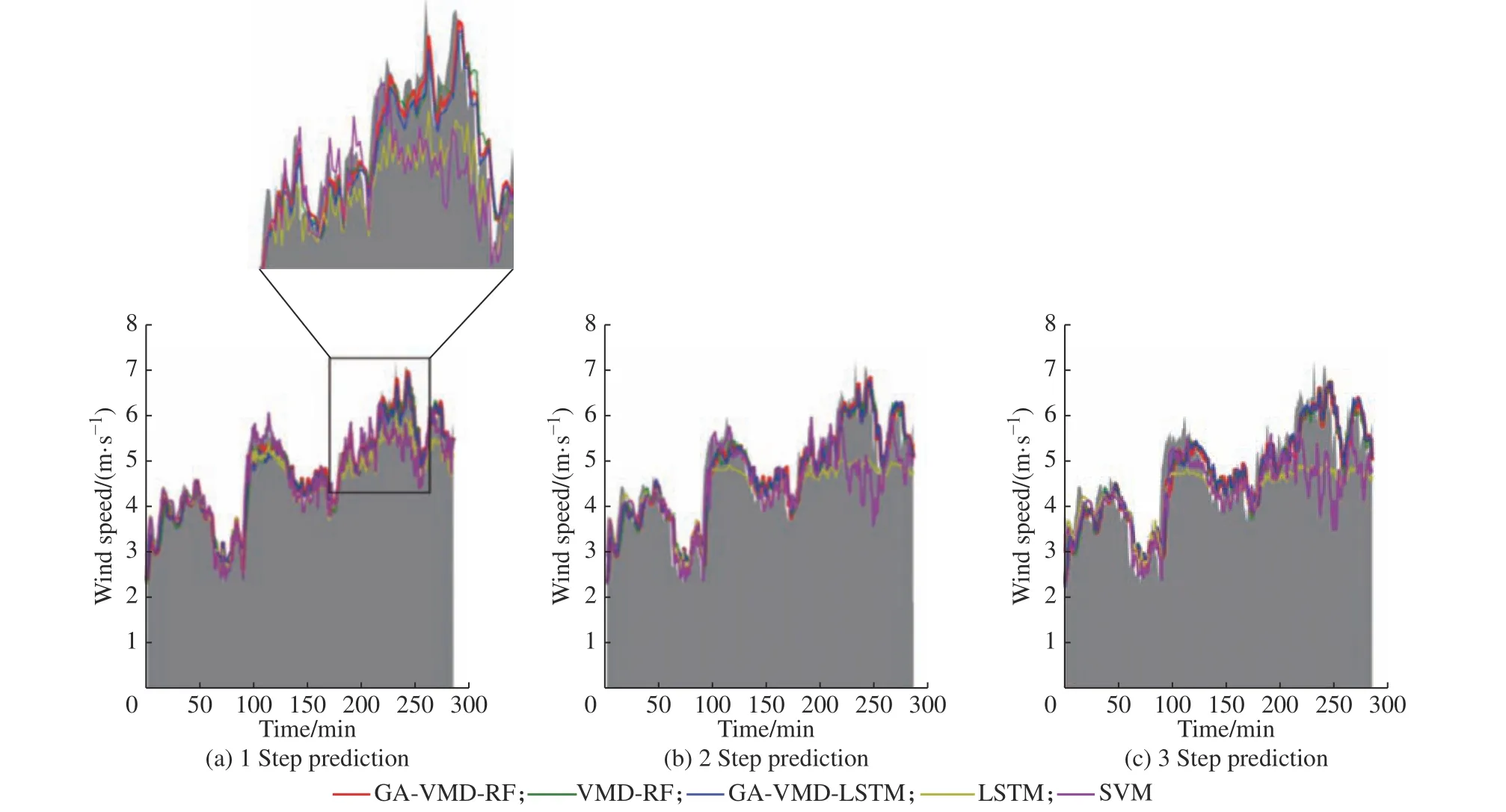
图8 数据集3 预测结果Fig.8 Predication result of dataset 3

为了更加清楚地定量对比各算法，将所有实验结果的MAE、MAPE、RMSE 指标作图，如图9 所示。其中每种算法同颜色的三柱从左至右依次表示MM、IT、MO 的结果。

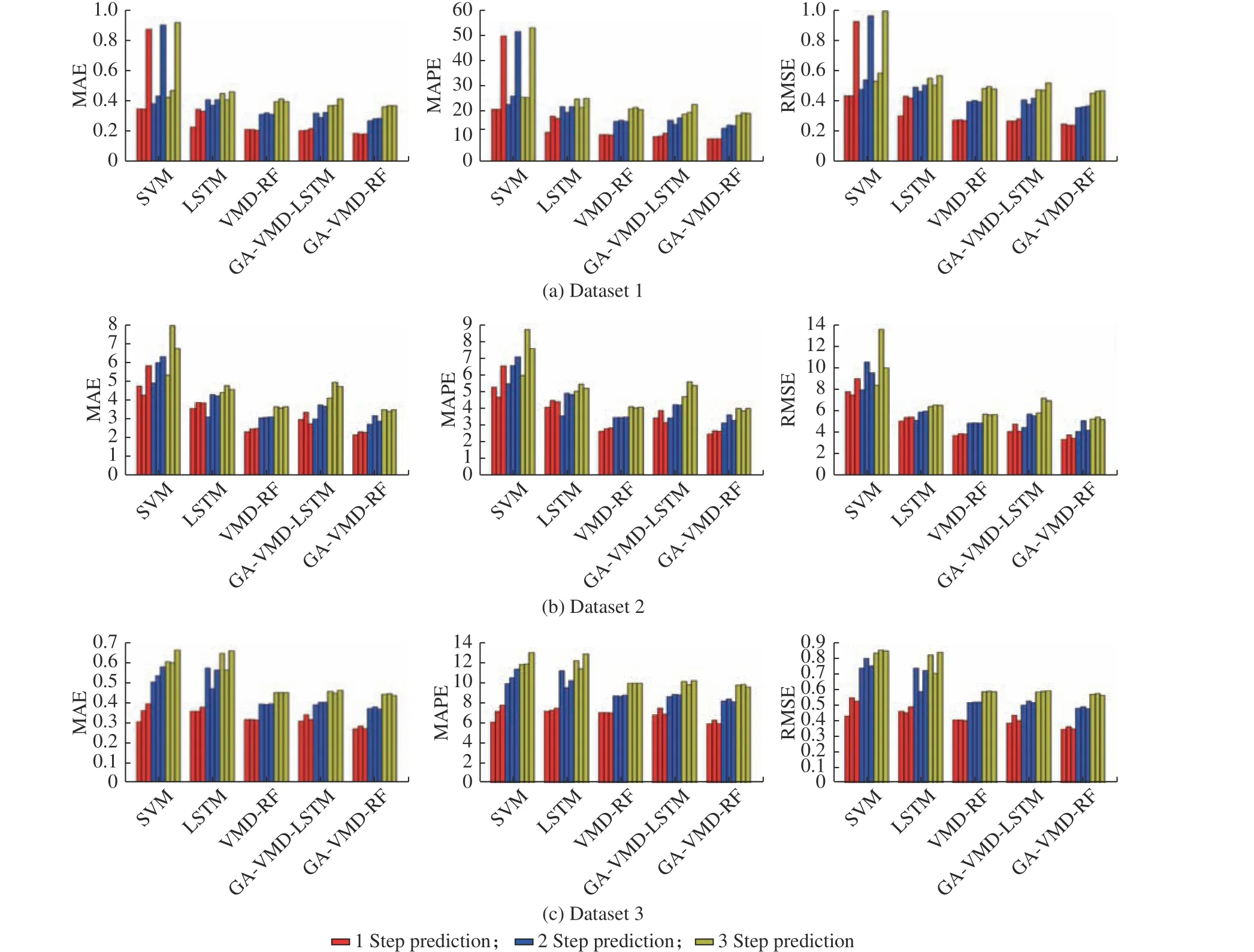
图9 数据集1～3 预测误差指标Fig.9 Predication error indicators of dataset 1～dataset 3

观察图9 可以发现：（1）对比单一预测模型算法SVM 和LSTM，所提出GA-VMD-RF 算法的MAE、MAPE 和RMSE 在数据集1～3 的预测步1～3 上均有显著的下降，如数据集1～3 的预测步1～3 的MAPE平均降低了51.9%、47.5%、18.3%；31.1%、28.6%、18.7%和47.1%、37.3%、23.4%；（2）对比不经参数优化的VMD 分解预测算法VMD-RF，所提出GAVMD-RF 算法的MAE、MAPE、RMSE 3 个指标在数据集1～3 上平均降低了7.7%、8.1%、7.8%，说明GA优化的VMD 对于预测性能确有提升；（3）对比于基于LSTM 模型的混合算法GA-VMD-LSTM，所提出算法GA-VMD-RF 的MAE、MAPE、RMSE 3 个指标在数据集1 上平均降低了9.1%、11.1%、8.6%，在数据集2 上平均降低了21.0%、21.0%、17.2%，在数据集3 上平均降低了8.0%、7.5%、7.5%，在数据集2 上表现更优，体现了RF 在不同模态建模方面的优势；（4）对比MM、IT、MO 这3 种多步预测策略，多模型多步预测（MM）总体上具有更高的预测精度，因此被作为GA-VMD-RF 算法最终所采用的策略。此外，虽然本文所提出的GA-VMD-RF 算法的MAPE 在3 个数据集上接近或超过10，看似比一些文献结果更大[14-16]，但仔细对比可以发现，这是因为采用了实时分解策略导致的，尽管精度有所下降，但却具有实际可应用性。

5 结束语

本文针对具有强非线性、波动性和不平稳性的复杂模态时间序列预测问题，提出一种基于遗传算法优化变分模态实时分解和随机森林的多步预测算法：引入排列熵来度量分解子序列的复杂度，采用遗传算法优化时序分解过程；充分利用随机森林算法通过样本扰动获得的数据挖掘优势，对不同模态的子序列分别建立差异显著的预测模型；将所有的分解和建模过程建立在实时分解框架下，使算法具有可用性。通过多个公开数据集的实验，得到采用多模型多步预测策略较优的一般性结论。最终所提出的GA-VMD-RF 算法的1～3 步预测结果相比于其他4 种对比算法预测精度更高、性能更稳定，误差指标MAE、MAPE 和RMSE 分别平均降低22.6%、21.7%、21.5%。