混合型抗机器学习攻击的强PUF 电路设计

翟官宝， 汪鹏君， 李 刚， 庄友谊

（温州大学电气与电子工程学院, 浙江温州 325035）

随着物联网和先进通信技术的发展，万物互联时代已经到来。当前数量庞大的电子设备已广泛应用于人们的生产、生活等各个方面。这些设备通常涉及大量敏感信息，一旦发生泄露，将对公众隐私和财产、甚至人身安全构成威胁。面对层出不穷的攻击技术，研究人员提出各种加密算法和安全防御技术，以增强系统的安全性和可靠性。但大多数物联网设备受其硬件资源、成本和计算能力等约束，传统加密和认证技术难以得到广泛应用，而物理不可克隆函数(Physical Unclonable Function, PUF)作为一种物理安全原语，利用制造过程中引入的不可控随机工艺偏差生成设备独有的数字指纹[1]，为解决该问题提供了一种全新的方案。最早的PUF 由Pappu 等[2]于2002 年提出，随着研究的深入，已涌现出各种不同类型的PUF 电路。对PUF 电路施加一组n比特激励C，对应生成m比特响应R。激励C和响应R合称为PUF 电路的激励响应对(Challenge Response Pair, CRPs)。根据PUF 生成CRPs 能力的不同，将其分为弱PUF 和强PUF[3]。弱PUF 产生CRPs 的数量有限，通常应用于安全密钥提取，典型的弱PUF 有SRAM-PUF、DRAM-PUF、蝶形PUF 等。强PUF 能生成指数级数量的CRPs，适用于系统设备认证和低成本身份验证[4]，主要包括APUF、RO-PUF 及电流镜PUF 等。对于强PUF，其CRPs 均借助相同单元的制造工艺偏差生成，因此CRPs 之间存在着内在关联，容易受 到如逻辑回归(Logistic Regression, LR)、人工神经网络(Artificial Neural Network, ANN)、支持向量机(Support Vector Machine, SVM)等机器学习(Machine Learning, ML)算法的攻击。

目前，防御ML 攻击的技术主要分为两类：一类是对PUF 电路结构进行非线性处理；另一类是设计专用电路对PUF 的激励或响应进行模糊处理。对于前者，主要通过在PUF 电路中引入非线性或设计新型结构单元改造PUF 电路，使电路模型线性不可分，因而能抵抗部分ML 攻击。Gassend 等[5]在APUF 中引入前馈回路，将中间级的判决结果作为后级开关单元的激励，提出前馈APUF(Feed Forward APUF,FF-APUF)；Machida 等[6]提出双APUF(Double APUF,DAPUF)，将输送至仲裁器判决的信号按交叉互换原则进行配置，提升PUF 抗攻击性能。对于后者，激励和响应之间的映射关系被扰乱，攻击者难以直接获取它们的对映关系，构建电路模型的成本和难度均得以提高。文献[7] 将多个并行的APUF 输出进行异或混淆处理后再输出，提出异或APUF(XORAPUF)；文献[8] 利用弱PUF 作为真随机数发生器，将产生的随机数与原始激励进行异或混淆，所得结果作为输入至APUF 的实际激励，提出轻量级PUF(Lightweight PUF, LSPUF)。然而，随着性能更加优异的ML 算法被不断提出，上述抗攻击方法也面临着失效的威胁。因此，通过对PUF 电路抗攻击电路结构和ML 攻击方法的研究，提出一种混合型抗机器学习强PUF 电路(Hybrid Strong PUF, HS-PUF)。该电路基于传统现场可编程逻辑门阵列（Field Programmable Gate Array，FPGA）电路结构而实现，有机结合两种抗ML 攻击方法，在确保稳定性的同时，能有效提高抗攻击效果。利用FPGA 对HS-PUF 进行实验验证，采用经典ML 攻击方法分析其抗攻击性能，并对随机性、唯一性及硬件资源开销等关键技术指标展开评估。

1 理论基础

1.1 ML 攻击方法

ML 能使计算机在未被编程情况下获得自主学习的能力[9]，应用于PUF 电路攻击领域表现为：若将收集到的部分CRPs 用于训练学习，ML 可根据训练的结果构建一个完整的数学模型，该模型可用来预测PUF 电路输出响应，相当于对PUF 电路进行“数学克隆”。由于APUF 电路模型属于线性方程，因此PUF 生成的CRPs 线性可分，APUF 安全性易受到威胁。

ML 算法根据训练集样本的不同，可分为监督学习算法、无监督学习算法和强化学习算法[10]。监督学习算法训练集中的样本均有标签，在训练过程中使用标签进行模型构建的调整，可使预测的精度不断提升，最终正确预测未知数据集；无监督学习正好与监督学习相反，训练集中未设置标签，可根据解决问题的不同分为关联分析、聚类问题以及维度约减；强化学习的样本需要通过和环境不断进行交互而获得，区别于监督学习算法需要通过人工收集并标注。

常用的ML 算法包含LR、ANN 和SVM 等。LR 算法属于广义上的线性回归模型[11]，其输出是在线性回归计算结果的基础上，利用Sigmoid 函数将其转换成概率值，可表示为：

其中y表示线性回归函数值。LR 具有结构简单、计算量小、功能强大等特点，适用于线性分类问题的模型构建。SVM 的目标是找到一个分离超平面，使样本数据集中的每个样本到超平面的距离最大化，样本到超平面的距离可表示为：

其中：w为法向量，表示超平面的方向；x表示样本点；b表示超平面到原点的距离；n表示样本数。借助超平面，SVM 能处理线性不可分问题，利用核函数到高维度空间中寻找分离超平面，使低维度空间下线性不可分的样本数据在高维度空间中线性可分。ANN 是由大量相关的神经元相互连接而成的复杂网络[12]。按照功能对网络进行划分，可分为输入层、隐藏层和输出层，其结构如图1 所示。通过调整神经元之间的权值可以实现对任意非线性函数的拟合，因此适合用来处理较复杂的非线性问题。

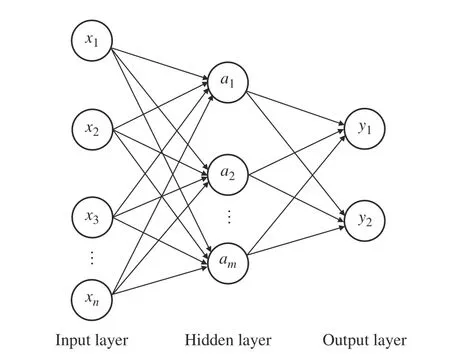
图1 ANN 结构示意图Fig.1 ANN structure diagram

1.2 APUF 电路结构与模型

APUF 属于研究最广泛的一类PUF 电路，XORAPUF、DAPUF 等PUF 电路都是以APUF 作为基本单元。传统APUF 电路结构如图2 所示，由n个开关单元级联而成的信号延时路径和仲裁器单元组成。在信号延时路径的初始端施加同一脉冲信号，经两条对称的延时路径传输后，由仲裁器对上下两条路径输出的信号进行仲裁，若上路信号先于下路信号到达仲裁器，则输出逻辑1，反之则输出逻辑0，即得到1 位响应。理想状态下，信号经两条对称的延时路径传输后应同时到达仲裁器，然而决定信号延时路径的开关单元间存在工艺偏差，导致信号到达仲裁器的时间存在差异，产生不可预测的“0”或“1”。开关单元由两个平行设置的多路选择器(MUX)组成，当施加给开关单元的激励信号C为“0”时，信号直接通过平行路径；当施加的激励信号C为“1”时，信号选择交叉路径通过。因此，在信号沿着延时路径进行传输时，可通过控制激励信号C改变信号的传输路径，影响上下路信号延迟差，产生不可预测的响应r。

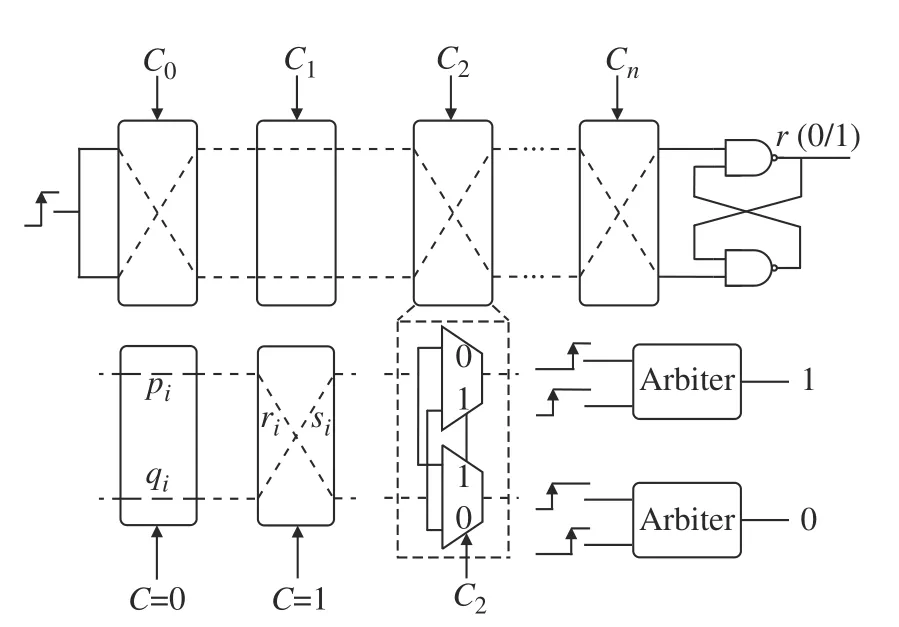
图2 传统APUF 电路结构Fig.2 Structure of the traditional APUF circuit

传统APUF 电路通常可用一个线性累加延时模型来表示[13]。到达仲裁器的信号总延迟偏差为信号通过每一级开关单元时存在延时偏差的累加，可表述为：

其中P是与激励向量C相关的奇偶校验向量。它们的关系可表示为：

其中pk与ci分别为奇偶校验向量P和激励向量C的子元素。ω是含各级开关单元延时参数的常数向量，各个开关单元的延时差可表达为：

其中αi，βi对应的计算公式分别如式(6)和式(7)所示：

其中pi、qi和ri、si分别表示信号平行通过与交叉通过时延时路径上的延时参数，如图2 中所标注。APUF 输出响应r与 ∆ 之间的关系可由式(8) 表示，若 ∆ >0，则APUF 输出响应为1，反之则为0。

其中sgn 函数取值范围为{-1，1}。

2 HS-PUF 电路设计

2.1 基于APUF 的抗ML 电路结构

2.1.1 2-1DAPUF 2-1DAPUF[14]是在如图3(a) 所 示的DAPUF[6]电路结构基础上将其两位输出异或处理，电路结构如图3(b) 所示。与图3(c) 所示2XORAPUF[7]电路类似，2-1DAPUF 也需设置两个并行的APUF，并将两个APUF 单元的输出异或混淆以得到1 位PUF 响应。这两者的主要区别在于：2XOR-APUF选取不同类型延时路径上的传输信号送至仲裁器模块进行判决，而2-1DAPUF 的每个仲裁器模块的比较信号均来自相同类型延时路径。2-1DAPUF 优点是能有效补偿FPGA 平台实现的APUF 信号延时路径不对称问题，抗ML 攻击能力比2XOR-APUF 高，尤其是依赖寻找分离超平面线性分离响应的ML 算法。然而，该PUF 对来自神经网络的攻击表现弱。

图3 抗ML 攻击电路结构Fig.3 Anti-ML attack circuit structure

2.1.2 FF-APUF FF-APUF[5]的电路结构如图3(d)所示。其响应生成原理与APUF 类似，通过判决两条平行延时路径上的信号延迟偏差获取不可预测的响应r。与APUF 不同的是：FF-APUF 在电路结构中引入部分前馈回路。前馈回路主要结构为与非门仲裁器，利用中间级开关单元输出信号的延迟差产生后级开关单元的输入激励，可根据部分信号的延迟偏差动态调整PUF 输入激励信号集。对于攻击者，隐藏的激励信号无法获取，难以预测激励响应映射关系，无法构建电路数学模型，因而提高了抵抗ML 攻击的能力。

2.1.3 混合PUF 电路结构 抵抗ML 模型攻击的另一个有效方法是增加电路结构的非线性。然而，对基于信号延时的PUF 电路，保持输入激励集恒定会降低非线性结构的抵抗ML 攻击效果。因此，将2-1DAPUF和FF-APUF 电路结构相互融合，可得到如图4 所示的混合PUF 电路结构（其中S 表示开关单元）。该结构通过加深电路结构的非线性化程度以及实现输入激励集动态调整，可增强PUF 随机性特征，提高抵御建模攻击能力。

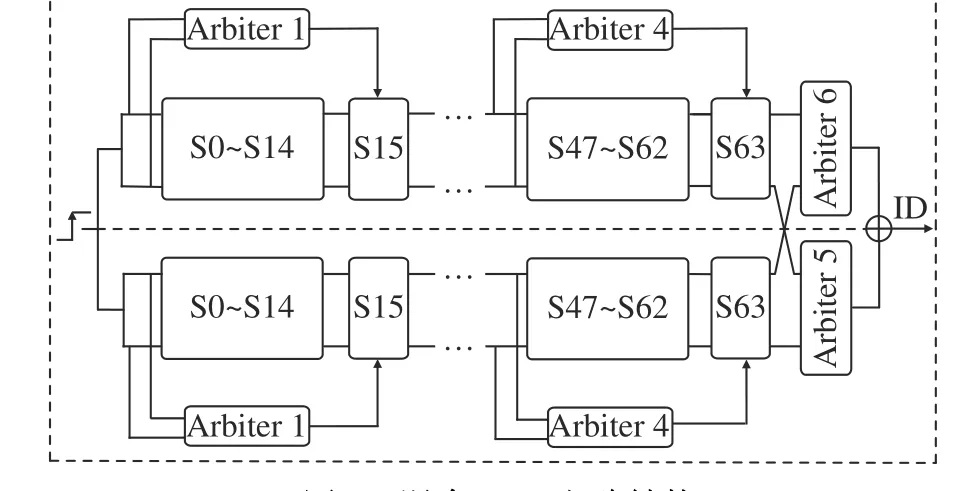
图4 混合PUF 电路结构Fig.4 Circuit structure of hybrid PUF

2.2 前馈回路数量的确定

前馈回路主要结构为交叉耦合与非门构成的仲裁器，其数量合理与否对PUF 电路稳定性和抗ML 攻击效果有很大影响。为确定电路结构中引入前馈回路的合理数目，对其回路数量与PUF 稳定性、安全性及电路硬件开销之间的关系进行实验探究，结果如表1 所示。由表可知，当选择前馈回路数量为4，输入与输出间隔15 个开关单元的插入方式时，其稳定性和安全性更具优势且硬件资源开销相对较小。

表1 PUF 相关指标随前馈回路间隔开关单元数量变化规律Table 1 Variation law of PUF related indexes with the numbers of feedforward loop interval switch units

2.3 路径交叉结构

为扩大信号延时路径的选择范围，同时实现开关单元最大利用程度，将对称设置开关单元输出的下延时路径与上延时路径相互交叉，输入激励互相倒置，可得到如图5 所示路径交叉结构和功能波形图。在原APUF 开关单元S1 输入端和镜像APUF 开关单元S1 输入端施加信号，因延时路径交叉，原APUF 开关单元S1 输出端IN2-2 信号不再由IN1-2 信号决定而是选自镜像APUF 开关单元S1 输入端IN1-3 信号，区别于信号原来只能选择在原APUF 单元延时路径上传输，现在可通过交叉结构选择在镜像APUF 延时路径上传输。不同开关单元和激励信号确立的延时路径不同，脉冲信号在传输时所消耗的时间各不相同。增加延时对比信号多样性，可有效改善输出响应随机性特征。

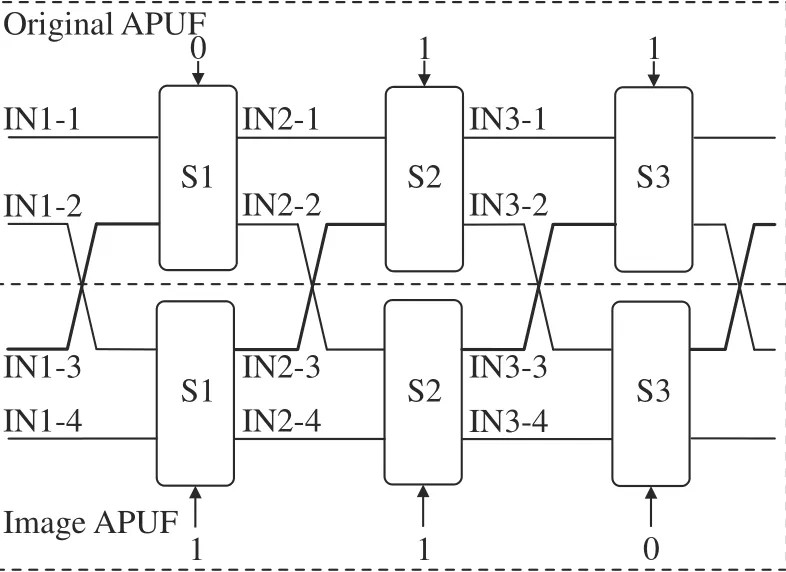
图5 路径交叉结构及其功能分析Fig.5 Path crossing structure and functional analysis

2.4 HS-PUF 电路结构

综上分析，可得本文HS-PUF 电路结构（图6）。首先，采用64 个路径开关单元和1 个仲裁模块以相互级联的形式构建传统APUF 电路，其中路径开关单元由两个平行设置的MUX 组成，仲裁模块则由两个耦合交叉的与非门构成；其次，在相邻位置按同样方式构建另一个APUF 电路，称为镜像APUF，并确保原APUF 与镜像APUF 平行且对称，对两个APUF 电路输出进行异或混淆，得到HS-PUF 电路1 位输出响应；然后，在原APUF 和镜像APUF 电路分别引入数量为4 且输入与输出间隔为15 个开关单元的前馈回路，实现输入激励信号集动态调整。最后，原APUF各开关单元的下延时路径与镜像APUF 对应开关单元的上延时路径进行交叉互换，输入激励相互倒置，以增加对比延时信号数量，提高PUF 响应随机性。

图6 HS-PUF 电路结构Fig.6 HS-PUF circuit structure

3 实验结果与分析

3.1 实验平台

HS-PUF 电 路 采 用Xilinx Artix-7 FPGA (XC7A 100T) 开发板实现，并利用Xilinx ISE 14.7 和Xilinx PlanAhead 14.7 工具对PUF 电路分别进行逻辑综合和布局布线。采用如图7 所示的测试系统进行相应测试：首先，PC 端利用Matlab 并结合FPGA 开发板自带的MicroBlaze 嵌入式微控制器实现测试平台的搭建，通过PC 端通讯接口集成的通用异步收发传输 器 (Universal Asynchronous Receiver/Transmitter,UART)模块发送生成的随机激励至FPGA；其次，通过FPGA 的UART 模块接收来自PC 端的激励数据，由MicroBlaze 完成对数据的处理，驱动FPGA 各硬件电路实现周期性方波信号的发生，PUF 电路响应生成以及输出响应的回传；UART 模块在接收到输出响应后，将其发送至PC 端；最后，PC 端利用接收到的响应信号，结合Matlab 实现对信号的分析处理。

3.2 抗攻击能力分析

实验基于经典LR、ANN 和SVM 算法对各个抗攻击结构分立作用时的PUF 电路及HS-PUF 电路进行建模攻击。各算法对不同PUF 攻击预测率与所用模型的训练CRPs 数量关系如图8 所示。由图8可知，当训练所用CRPs 数量小于104时，APUF、2XOR-APUF、FF-APUF 3 种ML 算法的预测率总体上增长较快；当训练所用CRPs 数量达到104时，算法预测率缓慢增长且趋于稳定。

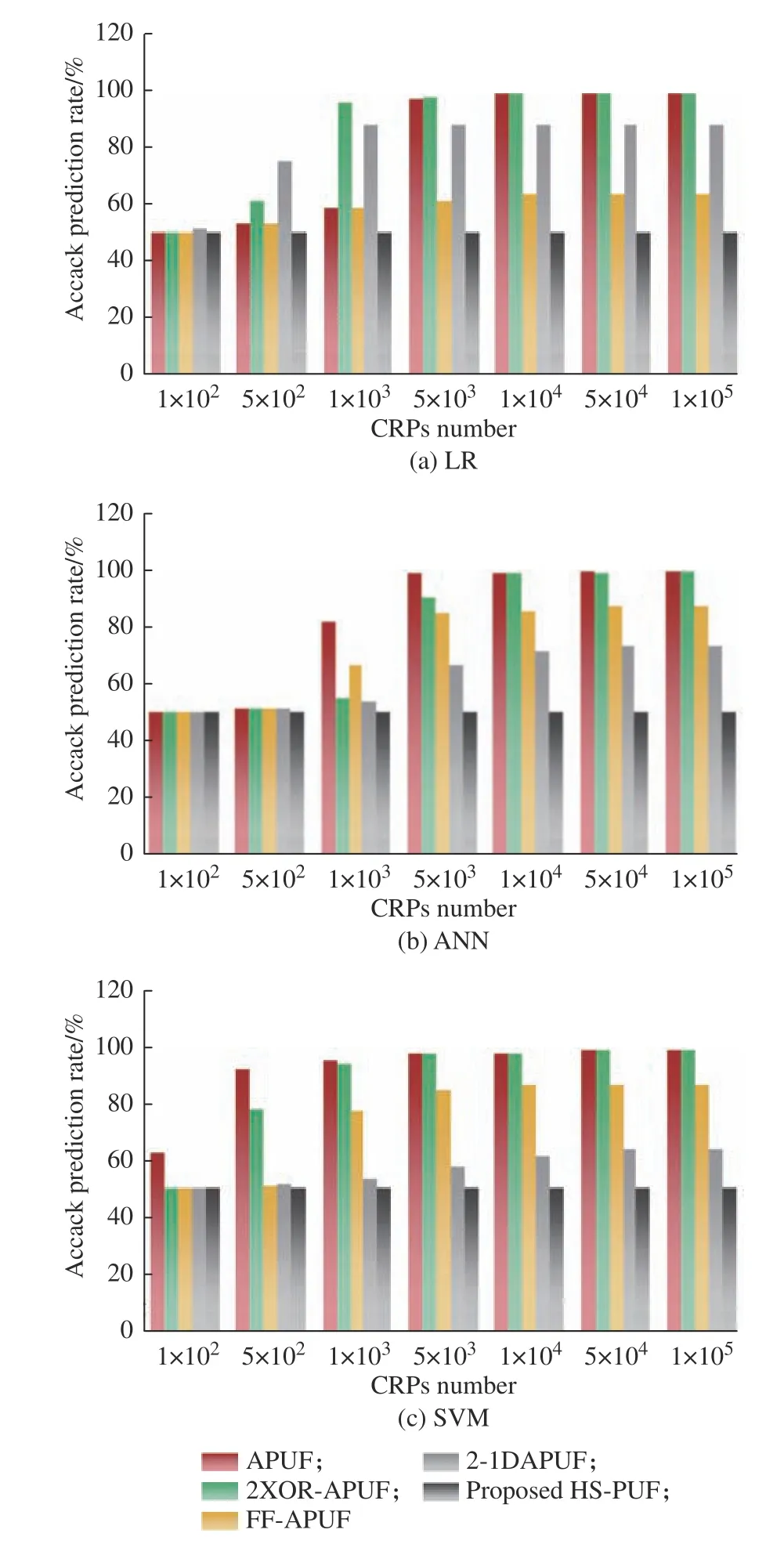
图8 各算法攻击预测率与训练CRPs 数量关系Fig.8 Relationship between the attack prediction rate of each algorithm and the numbers of trained CRPs

LR 算法攻击预测率如图8(a) 所示，可以看出HS-PUF 电路的攻击预测率低于前4 种PUF 电路，且当训练集接近105时，预测率仍接近50% 的理想值。ANN 算法攻击预测率与训练所用CRPs 数量关系如图8(b) 所示，可以看出在ANN 算法攻击下，2-1DAPUF 攻击预测率随CRPS 数量增加有所上升，表明ANN 相较LR和SVM 攻击预测能力更强，然而即使在ANN 算法攻击下HS-PUF 仍具备较强抗攻击能力。SVM算法攻击预测率与训练所用CRPs 数量关系如图8(c)所示，所得结论与LR 和ANN 类似。综上所述，HS-PUF 具有较强的抗攻击能力。

3.3 统计特性分析

3.3.1 随机性 随机性用来表征PUF 响应中0/1 分布情况[7]。理想情况下，逻辑0/1 在响应中随机出现且占比均匀不具偏向性。利用逻辑1 在输出响应中的统计值计算PUF 的随机性，计算式如式（9）所示。

其中：Ri代表第i位响应，N表示响应位数。统计实验数据测得响应中逻辑1 占比为50.24%，接近理想值50%。为直观显示PUF 随机性，常借助灰度图对随机性进行辅助描述。输出响应的灰度映射如图9(a)所示，其中黑色像素代表1，白色像素代表0，可以发现所提PUF 输出响应在灰度图像中黑白色素交替，表明响应中0/1 分布较为均匀。此外，对30 个PUF实体的灰度映射进行平均化处理，所得平均灰度映射如图9(b)所示，可以发现平均灰度值在0.5 附近波动。为反映输出响应间相关程度，利用自相关函数(Autocorrelation Function, ACF)对PUF 响 应 进 行 测试，测试结果如图10 所示。结果显示，在95%置信区间内，HS-PUF 响应的ACF 值为0.012 5，接近理想值0，反映出响应具有良好的空间独立性。

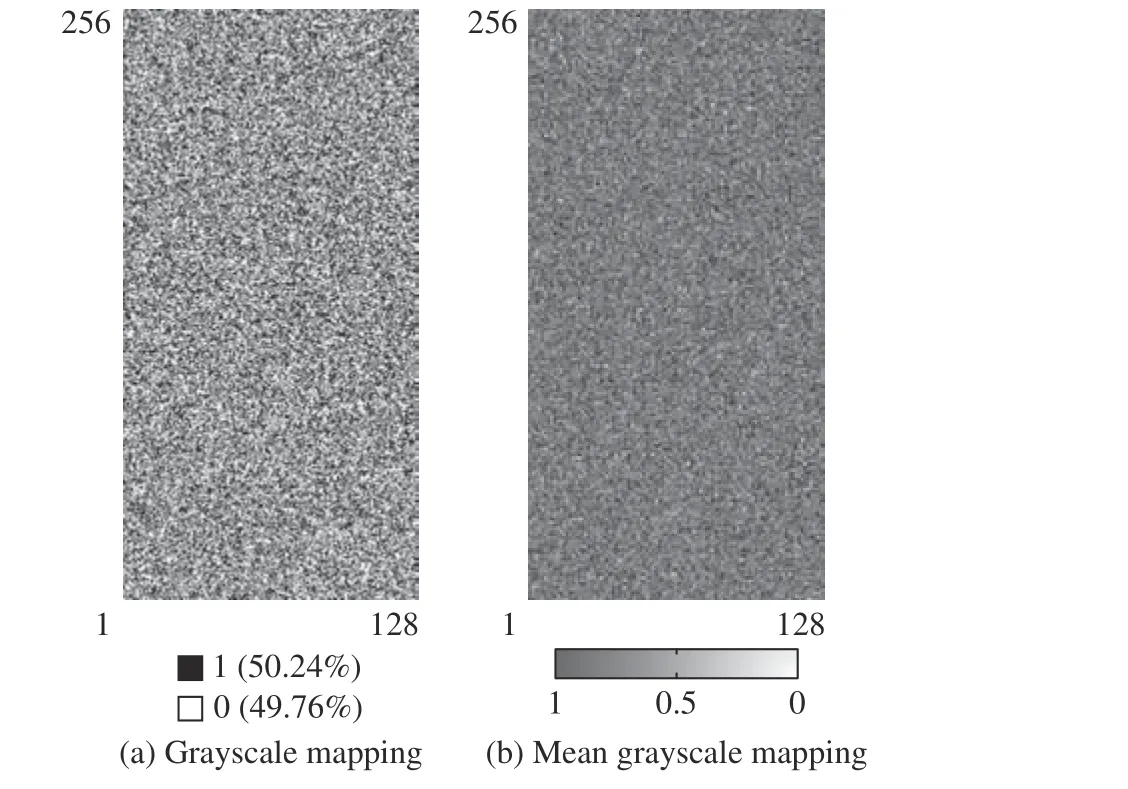
图9 输出响应0/1 灰度映射Fig.9 Output response 0/1 grayscale mapping

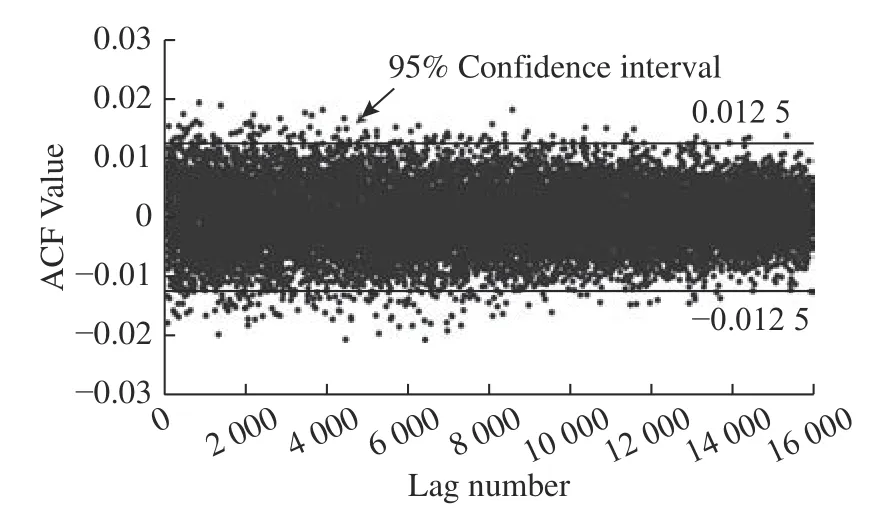
图10 HS-PUF 自相关性Fig.10 HS-PUF autocorrelation

3.3.2 唯一性 唯一性被用来标识不同PUF 个体间差异，一般采用平均片内汉明距离(Inter-Hamming Distance, Inter-HD)进行衡量[15]。理想情况下，相同激励作用于两个不同PUF 时，输出响应间应有一半比特位互不相同。数值上，通常采用相同激励作用于K个不同PUF 个体时，输出响应间不同位数的统计值来表示随机性。唯一性计算式如式（10）所示。

其中Ri和Rj分别表示第i个和第j个PUF 在相同激励作用下生成的n比特响应。唯一性可采用平均Inter-HD 的统计直方图形象化表示。HS-PUF 的平均Inter-HD 的统计直方图经归一化处理和高斯拟合后，所得曲线如图11 右半部分所示，测得数学期望（μ）和方差（σ）分别为0.500 4 和0.031 8，对应的唯一性为50.04%，接近理想值，表明HS-PUF 具有良好唯一性。

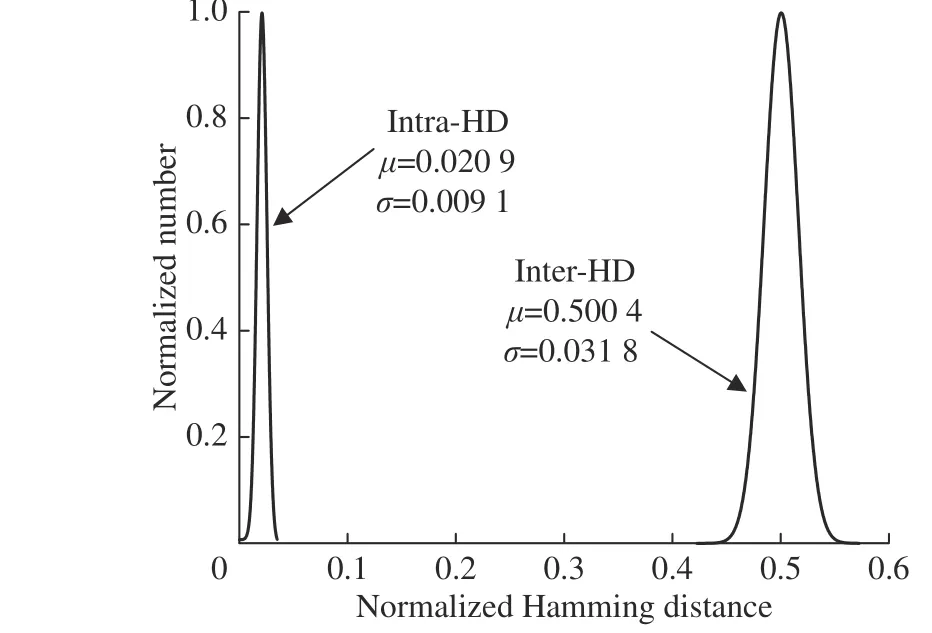
图11 HS-PUF 片间汉明距离与片内汉明距离拟合曲线Fig.11 Fitting curves of Intra-HD and Inter-HD of HS-PUF

3.3.3 稳定性 理想条件下，PUF 电路在任何情况下给定相同的激励都能输出相同的响应。然而，受到环境温度变化、电源电压波动以及器件老化等因素影响[16]，响应中不可避免地会混入噪声。因此，有必要引入可靠性指标来衡量PUF 电路复现响应的能力。稳定性指标通常采用平均片间汉明距离(Intra-Hamming Distance, Intra-HD)来衡量，即通过比较相同激励作用下存在于不同环境或电压条件下相同PUF 个体输出响应间不同位数，稳定性计算公式为：

其中R和R′分别表示同一个PUF 在相同激励下生成的两组n比特响应。将HS-PUF 置于常温常压环境下对输出响应进行循环读取，所得高斯拟合曲线如图11 左半部分所示，归一化后所得平均Intra-HD 为0.020 9，对应可靠性为97.91%，表明HS-PUF 具有良好的可靠性。

3.4 硬件资源开销

表2 所示为HS-PUF 与APUF、FF-APUF、2XORAPUF、2-1DAPUF 电路硬件资源消耗数量对比，可以看出HS-PUF 消耗的触发器数量与其他4 类PUF 相当，消耗的查找表（LUT）数量较APUF 和FF-APUF有所增加，与2XOR-APUF 和2-1DAPUF 消耗的LUT 数量相当。

表2 各类抗ML 攻击PUF 电路硬件资源消耗对比Table 2 Comparison of hardware resource consumption ofvarious types of anti-ML attack PUF circuits

3.5 综合性能对比

采用LR、ANN 和SVM 3 种ML 算法分别对APUF、FF-APUF、2XOR-APUF、2-1DAPUF 以及HSPUF 进行攻击，攻击预测率统计数据如表3 所示。表中最终预测率均在训练集数量为105时获得，分析表格数据可知HS-PUF 抗攻击结构相较其他4 种PUF 电路具备更强的抗攻击能力，且实验数据统计分析表明HS-PUF 的随机性、唯一性和稳定性亦表现良好。

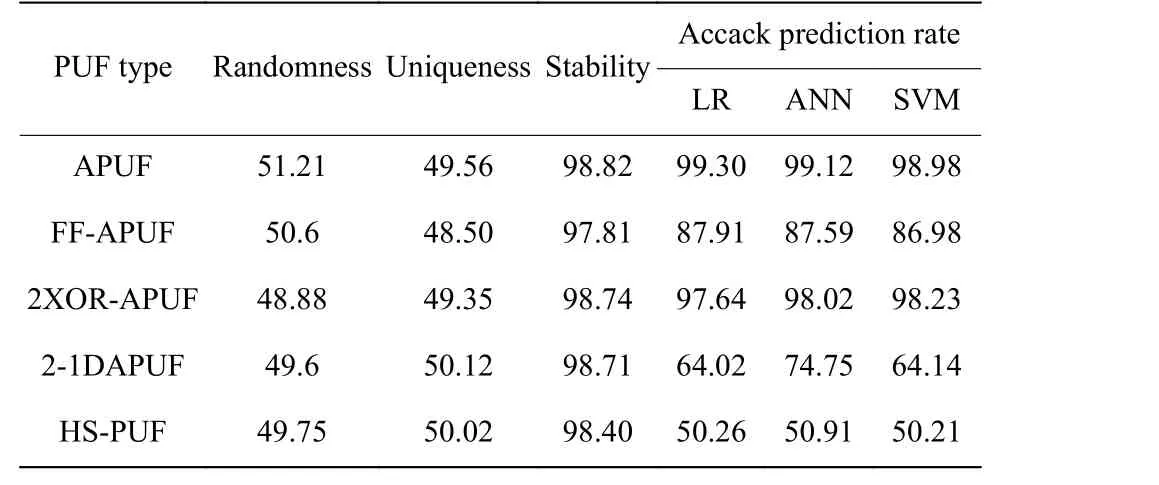
表3 各PUF 电路统计特性与抗攻击能力实验对比Table 3 Experimental comparison of statistical characteristics and anti-attack capability of each PUFcircuit (%)

4 结 论

针对强PUF 易受ML 建模攻击威胁问题，通过对PUF 抗攻击结构的研究，提出一种混合型强PUF 电路HS-PUF。该电路有机融合响应混淆处理和引入非线性结构等多种抗攻击方法，具有抗攻击能力强、硬件开销较小和易于FPGA 实现等特点。实验结果表明，即使训练所用数据集为105，用LR、ANN 和SVM 算法攻击HS-PUF 电路，攻击预测率仍处于较低水平，接近理想值50%。此外，统计特性分析结果亦表明HS-PUF 性能较为优异，可广泛应用于物联网认证设备等领域。