(1+1)维Maxwell-Chern-Simons-Higgs系统解的局部适定性
2024-01-05孟嘉乐
孟嘉乐
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
1990年,Lee等[1]研究了同时具有Maxwell项和Chern-Simons项的(2+1)维Maxwell-Chern-Simons-Higgs(MCSH)自对偶模型,该模型的拉格朗日函数为:
其中:gμν=diag(1,-1,-1)是R3上的(2+1)维闵可夫斯基度量;φ是复函数;N是实函数;A=(A0,A1,A2)是实规范场,满足Fμν=∂μAν-∂νAμ,Dμ=∂μ-ieAμ;e是电子的电荷;κ是Chern-Simons常数(κ>0).在该系统中,用希腊符号表示0,1,2,用拉丁符号表示1,2.对系统(1)进行变分可分别得到(A,φ,N)对应的欧拉-拉格朗日方程,为:

1 系统性质分析
假设系统(1)与变量x2无关,并将变量A2重新定义为B,由此得到的(1+1)维MCSH模型的拉格朗日函数为:
其中:gμν= diag(1,-1).同理,对(1+1)维MCSH系统进行变分可分别得到(φ,N,A,B)对应的欧拉-拉格朗日方程:
(2)

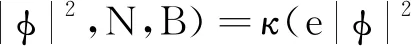
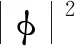
φ→φeiχ,Aμ→Aμ+∂μχ,B→B,N→N.
其中χ:R1+1→R是一个光滑函数.由上式可知,系统(2)的解可由规范等价对(φ,N,Aμ,B)组成.对系统(2)进行积分运算可得系统(2)的守恒能量为:
由上式可以看出,(φ,N,Aμ,B)有两种自然渐进条件可使能量有限,分别为:
(3)
在洛伦兹规范条件∂0A0-∂1A1=0下,(1+1)维MCSH系统的柯西问题可改写为:
(4)
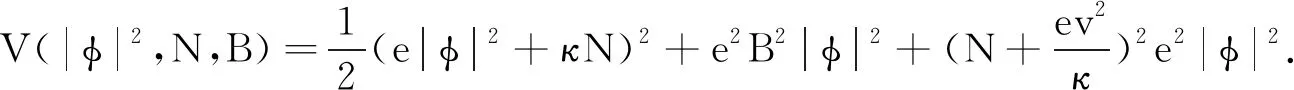
本文设系统(4)的初值为φ(0,·)=φ0, ∂t(0,·)=φ1,Aμ(0,·)=a0μ, ∂tAμ(0,·)=a1μ,B(0,·)=b0, ∂tB(0,·)=b1,N(0,·)=n0, ∂tN(0,·)=n1.且上述初值满足约束方程:
(5)
2 结果及其证明
定理1假设系统(4)的初值φ0∈H2,φ1∈H1,a0μ∈H2,a1μ∈H1,b0∈H2,b1∈H1,n0∈H2,n1∈H1,且上述初值满足约束方程(5),则MCSH系统(4)存在唯一的局部时间解,且满足:
φ∈C([0,T],H2(R))∩C1([0,T],H1(R)),
Aμ∈C([0,T],H2(R))∩C1([0,T],H1(R)),
B∈C([0,T],H2(R))∩C1([0,T],H1(R)),
N∈C([0,T],H2(R))∩C1([0,T],H1(R)).

引理2[5]令(u0,u1)∈Hs×Hs-1,h∈L1([0,T],Hs-1),则线性波动方程□u=h(x,t),u(x,0)=u0(x), ∂tu(x,0)=u1(x)存在唯一解,且其满足u∈C([0,T];Hs)∩C([0,T];Hs-1).即对于0≤t≤T,有如下能量不等式成立:
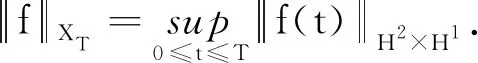
(6)
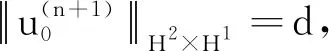

同理可得:
对其他项应用同样的估计方法并合并最终可得:
(7)
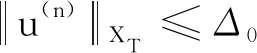

由上式可知F 为B→B上的压缩映射.由此再通过不动点定理即可得系统(4)存在唯一的解u∈C([0,T];H2(R))∩C1([0,T];H1(R)).
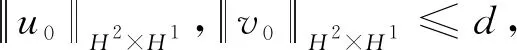


由上式可得□X=0为齐次线性波动方程,因此X∈H2×H1且唯一.再由文献[6]可知,对于任意的u(t)∈H3×H2始终有X∈H2×H1,因此有X=0,Y=0,即u(t)满足约束方程.定理1证毕.
