利用矩阵迹求解两类正交矩阵谱的研究

林志兴, 陈梅香, 杨忠鹏, 杨子斌

( 1.福建省金融信息处理重点实验室(莆田学院), 福建 莆田 351100;2.金融数学福建省高校重点实验室(莆田学院), 福建 莆田 351100; 3.福州大学 数学与统计学院, 福州 350108 )

0 引言

设C、R分别为复数域、实数域,Z为所有整数的集合.复数i∈C满足i2=-1.E(En)为n×n单位矩阵.AT、|A|、trA分别表示矩阵A的转置、行列式、迹.如果ATA=En,则称A∈Rn×n为正交矩阵.On×n为n×n正交矩阵集合,SOn×n为n×n对称正交矩阵集合,IOn×n为n×n特征值都为实数或为纯虚数的正交矩阵集合.称A∈Rn×n的特征多项式|xE-A|在C上的n个根(λ1,λ2,…,λn)为A的特征值,且记A的谱为σ(A)={λ1,λ2,…,λn}.

研究显示,在复数域上证明n×n矩阵特征多项式存在n个根具有较多困难[1].目前,利用Mathematic和Maple软件虽可计算求出一个中等规模矩阵的特征多项式,但对于n≥5的n×n矩阵仍无良好的求解方法[2].为此,许多学者利用不同的方法探讨了该问题,其中有些学者采用迹估计了矩阵特征值的上下界[3-11].1961年,Smith[12]首次用迹给出了3×3实对称矩阵特征值的计算公式;2018年和2020年,文献[13-14]的作者用迹研究了3×3正交矩阵的特征值.1999年和2011年,文献[15-16]的作者研究了3×3正交矩阵的迹等式;2020年,文献[17]的作者在文献[15-16]的基础上研究了更为一般的n×n正交矩阵的迹方程,并且得到了特征值全为实数或为纯虚数的正交矩阵类IOn×n(由后面的讨论可知,该IOn×n是平方对称的正交矩阵)的所有解的显示表达.另外,文献[15]和[18]的作者还得到了n×n正交矩阵为对合的充分条件,并用2个4×4正交矩阵的数值例子(该例子为平方对称和4次方幂对称)说明了使用该结论时应注意的问题.以上研究表明,平方对称和4次方幂对称的正交矩阵是较为常见的正交矩阵,因此研究求解这两类正交矩阵的特征值具有重要意义.

为此,本文从平方对称、4次方幂对称的这两类n×n正交矩阵的特征值与迹的关系入手,应用正交相似矩阵的特征值和迹的不变性得到了判定这两类矩阵为平方对称正交矩阵和4次方幂对称正交矩阵的充要条件,并在此基础上给出了相应矩阵的特征值及其重数的计算公式.将本文计算方法应用到已有文献中的数值例子上显示,该方法比传统方法(通过求解特征多项式来得到特征值)简单、方便.

1 预备知识

O-1AQ= diag(Et,-Es,W1,…,Wk)=OA,t+s+2k=n;

(1)

A∈SOn×n当且仅当式(1)中k= 0.

(2)

如同式(1),本文作如下约定:A∈On×n的特征值1和-1的重数分别为t和s;k为A的两两共轭的非实的特征值的对数,且OA为A的正交标准形.

引理2[17]设A∈On×n,σ(A)={λ1,λ2,…,λn},则对于A的每个特征值λj有:|λj|= 1,λj∈σ(A),且|A|=(-1)s, -1为A的s重特征值.

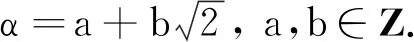
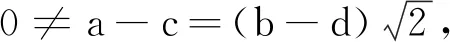
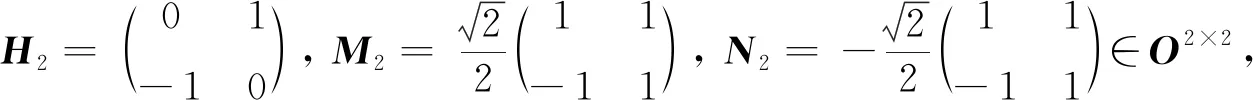
(3)

(4)

(5)

证明计算H2、M2、N2的特征多项式即可得到式(3)和式(4),再计算H2、M2、N2的平方或4次方幂即可得式(5)成立.证毕.

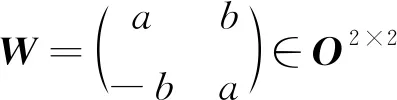
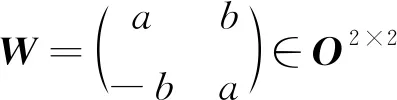
由引理5可直接得如下引理6.

2 特征值为实数或纯虚数时正交矩阵的谱和迹

定理1设A∈On×n,则A∈IOn×n当且仅当A2∈SOn×n.

A2=Qdiag(Et,-Es,W1,…,Wk)2Q-1=Qdiag(Et+s,-E2k)Q-1∈SOn×n.

(6)

(7)

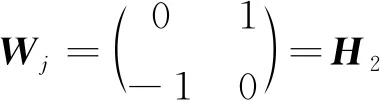
定理1表明,特征值全为实数或为纯虚数的正交矩阵与平方对称的正交矩阵是同一类的正交矩阵,因此用矩阵平方的对称性来确定IOn×n更为简单实用.

定理2设A∈On×n.若A2∈SOn×n,则A的所有可能的特征值为实数或纯虚数,且有:

(8)

(9)

证明由定理1知A∈IOn×n.由式(1)、(3)、(5)和引理6知式(6)和式(8)成立.由此再由式(1)和式(5)可得:

1)当A≠AT时,由式(1)、(2)、(8)可知k≠0.由此再由式(8)、(4)、(6)可得trA2=t+s-2k=t+s+2k-4k=n-4k,即:

(10)

2)当A=AT时,由式(1)、(2)、(8)知k= 0.再由式(10)知,式(9)仍然成立.证毕.

定理2表明,只用矩阵迹就可确定IOn×n中矩阵的谱的计算公式.

推论1设A∈On×n.若A2∈SOn×n,则有:

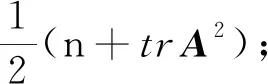
2)若trA>0,则t≥1;若trA<0,则s≥1;

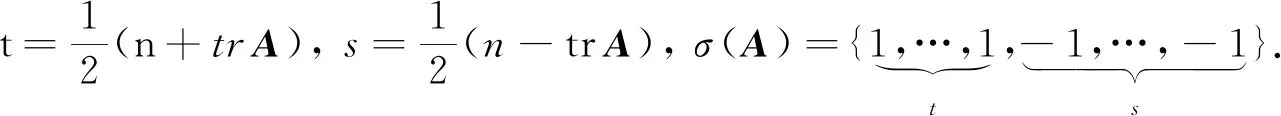
证明由式(9)可知推论中的1)成立.若trA>0(即trA≥1),则t=s+trA≥ trA≥1;若trA<0(即trA≤-1),则有s=t-trA≥ -trA≥1.由此得推论中的2)成立.

当A=AT时,由定理2中的2)可得A2=En,即trA2=n.由于SOn×n⊂IOn×n,因此式(9)成立,由此可知推论中的3)得证.证毕.

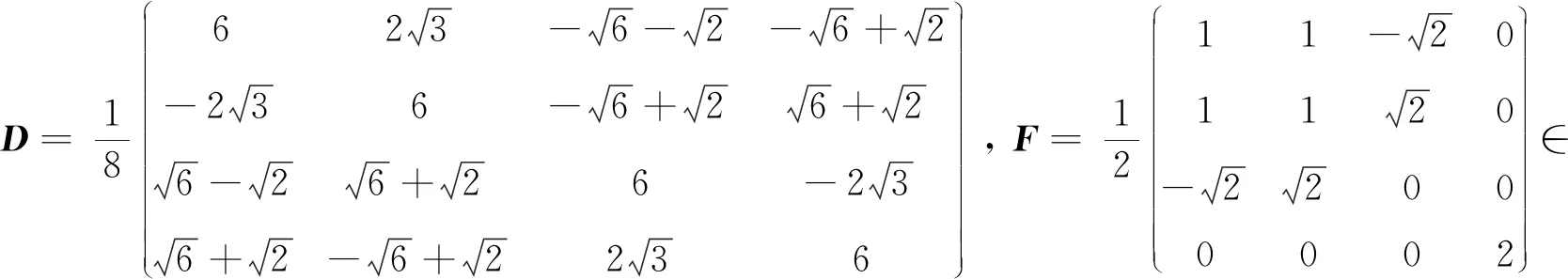
由文献[20]中的例6.2可知,F和Aj(j= 1,2,…,7)都是对称的.由于trF= trAj= 2(j= 1,2,…,6),因此由推论1中的3)可知,σ(F)=σ(Aj)={1,1,1,-1},j= 1,2,…,6.类似地,由trA7= 0和推论1中的3)可知,σ(A7)={1,1,-1,-1}.

例2请用本文的方法求出如下两组置换矩阵[20]的特征值和谱:

由于μ1,μ2,…,μ6是对称矩阵,且置换矩阵是正交的,因此μj∈SO4×4,j= 1,2,…,6.再由trμj= 2和推论1中的3)可知,μ1,μ2,…,μ6彼此为正交相似,且其正交标准形为diag(1,1,1,-1).

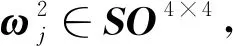
3 四次方幂对称的正交矩阵的谱和迹

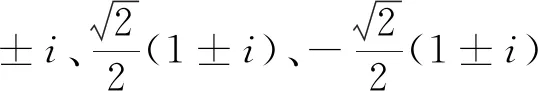
(11)

再由式(3)—(5)可得:

(12)

Q-1A4Q= diag(Et+s+2k1,-E2k2,-E2k3)=OA4∈SOn×n,n=t+s+2k1+2k2+2k3.

(13)

于是由式(13)知A4∈SOn×n,必要性得证.

②充分性.由于B=A2∈On×n,B2=A4∈SOn×n,因此由定理1可知B=A2∈IOn×n.设tB、sB、kB分别为B的特征值1和-1的重数以及特征值±i的对数,于是由式(6)、(8)、(9)可得:

(14)

U-1A4U=U-1B2U= diag(EtB+sB,-E2kB).

(15)

(16)

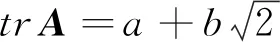
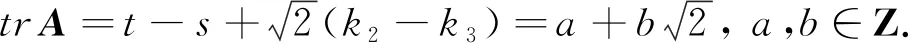
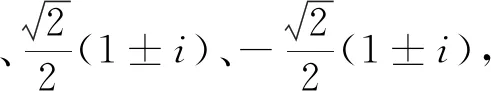
(17)

(18)

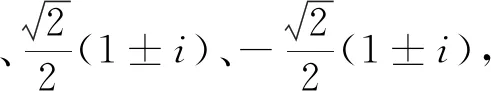
(19)

(20)

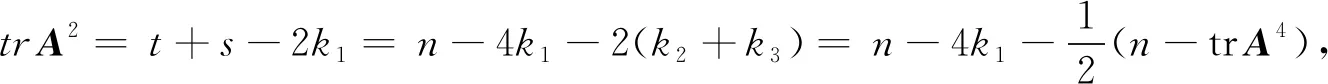
(21)

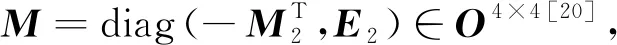
4 主要结论的应用

1962年,华罗庚在研究辛群的辛方阵的相似问题时,用简洁的方法再次得到了“两个正交矩阵正交相似的充要条件是它们的特征矩阵有相同的初等因子”[21]的结论.由初等因子理论易知,该结论与本文的引理1等价,由此进一步表明两个正交矩阵是否正交相似是由它们所有的特征值来确定的.

定理5设A,B∈On×n,则:

1)若A,B∈SOn×n,则A与B正交相似当且仅当trA= trB;

2)若A2,B2∈SOn×n,则A与B正交相似当且仅当trA= trB, trA2= trB2;

3)若A4,B4∈SOn×n,则A与B正交相似当且仅当trA= trB, trA2= trB2, trA4= trB4.

证明1)必要性.由矩阵正交相似的性质可知,当A与B正交相似时,Al与Bl也正交相似,因此trAl= trBl,其中l是任意的正整数.必要性得证.

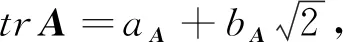
原有的相关文献都是通过求解特征多项式来求解正交矩阵的特征值,如例4、例5和例6,而本文仅采用矩阵迹即可求出正交矩阵的特征值.

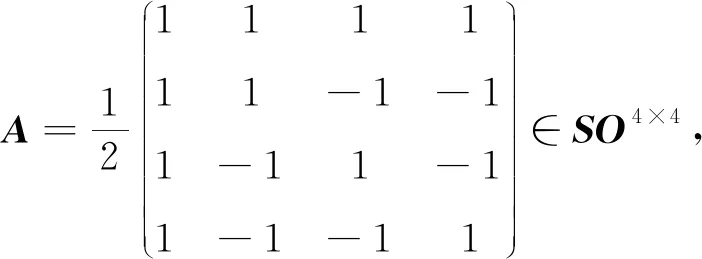
由trA= 2和定理5中的1)可知,A与例1中的F和Aj(j= 1,2,…,6)以及例2中的1)中的μj∈SO4×4(j=1,2,…,6)都是正交相似的.于是由推论1中的3)可知,它们的正交标准形为diag(1,1,1,-1).

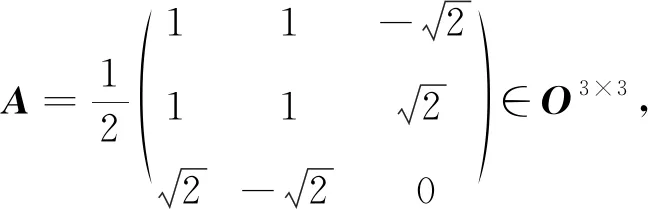
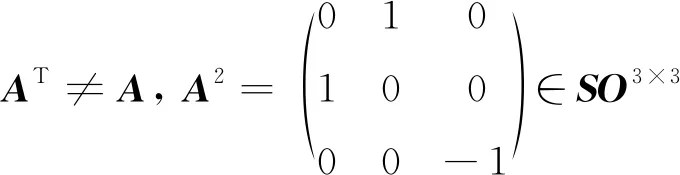
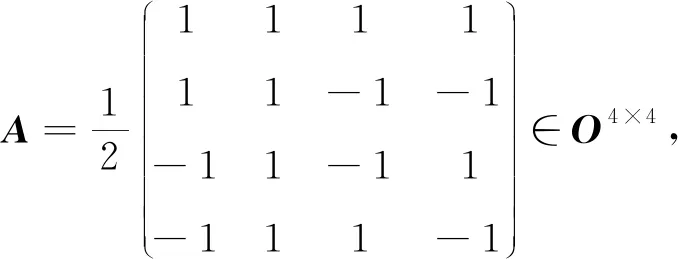
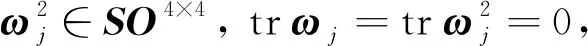
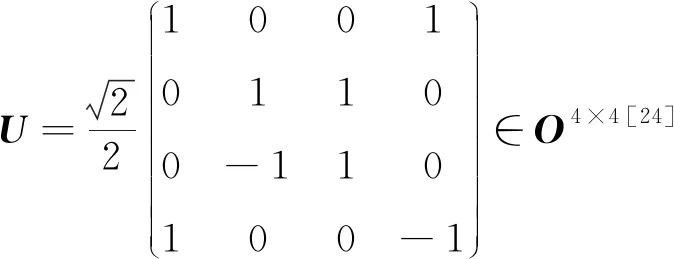
2)请用本文的方法求解A和U[15,18]的特征值.

(22)

由式(22)可知:

A2=-UT(≠E4), 且A4= (UT)2=U2=-E4∈SO4×4.

(23)

再由式(23)可知,U与A分别是平方对称、4次方幂对称的正交矩阵.由于 trU= 0, trU2=-4,因此由定理2和式(11)可得t=s= 0,k= 2,即

σ(U)={i,i,-i,-i}.

(24)

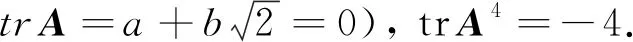
文献[15]和文献[18]给出了正交矩阵的一个重要结论:当A,U∈On×n,且U没有重特征值和UA=AUT时,必有A2=E.

式(22)中的2个矩阵是文献[15]中的定理6.5和文献[18]中定理1中的2个数值例子.由式(22)和式(23)可知,UA=AUT,A2≠E;因此,由式(24)可知文献[15]和文献[18]中给出的结论其前提条件“U无重特征值”是必不可少的.

文献[24]中的习题535、文献[26]5.3节中的习题22.3、文献[27]5.3节中的习题21.3都是应用正交变换将同一个二次型“2x1x2+2x3x4”化为标准形,但其所用的正交矩阵是各不相同的.应用本文方法计算这3个正交矩阵的特征值得:文献[24]所用的正交矩阵是平方对称的;文献[26]和文献[27]所用的正交矩阵是4次方对称的,且由定理5中的3)可知这两个矩阵是正交相似的.由此表明,将一个实二次型化为正交标准形时,可以使用不同的正交矩阵,且所使用的正交矩阵既可以是正交相似的,也可以不是正交相似的.

以上数值例子表明,利用矩阵迹求解平方对称和4次方幂对称的这两类正交矩阵的特征值,可不用通过求解特征多项式来求解,因此该方法比传统方法简单、实用.