概率语言术语集距离测度的改进及其应用

刘孟宇, 王惠文

( 云南师范大学 数学学院, 昆明 650500 )

0 引言

为了更好地通过定性的方式来描述实际生活中不能被定量表示的问题,1975年Zadeh[1]提出了模糊语言方法.由于模糊语言方法只能利用一个语言术语来评估语言变量,因此当决策者面临具有高度不确定性的问题时,该方法存在较大的局限性.基于此,2011年Rodriguez等[2]提出了犹豫模糊语言术语集(HFLTS)的概念.由于该概念将犹豫模糊集[3]和模糊语言方法相结合,允许决策者使用多个语言术语同时评估语言变量,因此其很好地弥补了模糊语言方法的缺陷;但由于HFLTS将决策者给出的每个语言术语赋予了相等的权重,因而其决策结果存在一定的偏差.为了解决HFLTS存在的这一缺陷,2016年Pang等[4]提出了概率语言术语集(PLTS)的概念.由于PLTS允许决策者将每个语言术语赋予不同的权重,因此使用PLTS可以获得更为准确的决策结果.

近年来,学者们已对直觉模糊集、犹豫模糊集以及区间模糊集等的距离测度进行了较多研究,但对PLTSs距离测度的研究相对较少.目前,对PLTSs距离测度进行研究的文献主要有:2016年,Pang等[4]给出了PLTSs偏差度的定义;同年,Zhang等[5]给出了概率语言术语集距离测度的定义;2019年,Mao等[6]基于PLTSs偏差度定义了一种新的PLTSs欧氏距离,但是该距离测度公式的计算精度需进一步提高.基于上述研究,本文定义了一种新的PLTSs距离测度,并通过实例验证了该距离测度的有效性.

1 基础知识

1.1 犹豫模糊语言术语集(HFLTS)

定义1[1]设τ是一个正偶数,则LTS可表示为:

S={si|i= 0,1,…,τ}.

(1)

由式(1)可以看出,LTS是一个由固定数量的语言术语组成的有限参考集,其中,τ+1是S的基数,si(i=0,1,…,τ)是语言术语,并且si(i= 0,1,…,τ)通常以下标为基准进行升序排列.

例1给定τ=6,则LTS可表示为如下形式:

S={s0=极其慢,s1=非常慢,s2=慢,s3=中速,s4=快,s5=非常快,s6=极其快}.

定义2[2]若S={si|i= 0,1,…,τ}是给定的LTS,则HFLTS是S上的连续语言项的有序子集.

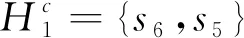
1.2 概率语言术语集(PLTS)

定义3[4]设S={si|i= 0,1,…,τ}是一个给定的LTS,则称定义在S上的PLTS为:

(2)

其中:L(k)(p(k))是概率语言术语元(PLTE),L(k)(k=1,2,…,#L(p))是L(p)上的可能的语言术语,p(k)∈(0,1](k=1,2,…,#L(p))是与L(k)(k=1,2,…,#L(p))相对应的概率信息,#L(p)是L(p)中的元素个数.在下文中,仅考虑标准化的PLTS,即仅考虑概率语言术语元的概率之和等于1的情况.

2 概率语言术语集的距离测度

定义4[7]L1(p)和L2(p)是任意两个PLTSs,定义它们之间的距离测度为d(L1(p),L2(p)),且d(L1(p),L2(p))满足以下3个性质:①d(L1(p),L2(p))≥0;②若L1(p)=L2(p),则d(L1(p),L2(p))= 0;③d(L1(p),L2(p))=d(L2(p),L1(p)).

2.1 传统PLTSs的距离测度

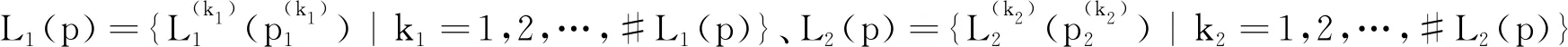
(3)

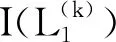
2.2 新的PLTSs的距离测度

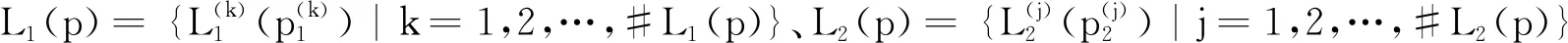
(4)

其中:ω(ω∈(0,1))是权重参数.

定理1定义6中的距离公式满足定义4中给出的PLTSs距离测度的3个公理性条件.

证明本文以标准化的汉明距离为例(λ=1)证明式(4)满足定义4中的3个公理性条件.

1)非负性显然成立.

2)因当L1(p)=L2(p)时,#L1(p)=#L2(p),所以显然有:

3)由

显然知有dgnd(L1(p),L2(p))=dgnd(L2(p),L1(p)),故对称性成立.综上,定理1得证.

由于s0.5τ是最模糊的语言术语,因此本文将定义6中的L1(p)与s0.5τ之间的偏离程度作为模糊性的参考.由此得到的L1(p)与{s0.5τ(1)}之间的汉明距离为:

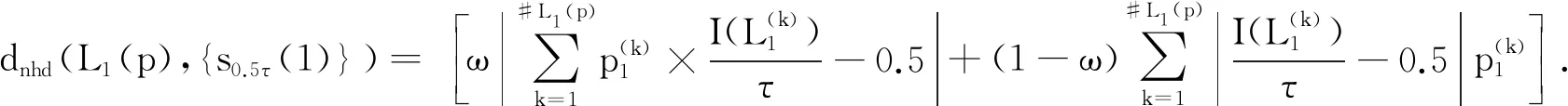
将上式代入模糊熵生成函数(f(x)=1-2x)[9]中可得概率语言术语集的熵测度公式:

E(L1(p))=1-2dnhd(L1(p),{s0.5τ(1)})=

(5)

由式(5)中的模糊熵可知,其与文献[10]中的混合熵的形式完全一样;但本文定义的熵测度更为简单,即不用再将基于距离的熵测度和基于伪距离的熵测度进行凸组合.以下举例说明本文提出的距离测度的合理性和有效性.

例3L1(p)={s3(1)}、L2(p)={s5(0.2),s7(0.8)}、L3(p)={s1(0.2),s6(0.4),s8(0.4)}、L4(p)={s3(0.6),s7(0.4)}是定义在S={si|i= 0,1,…,10}上的PLTSs,请计算它们两两之间的汉明距离.

L1(p)={s3(0.2),s3(0.4),s3(0.4)};L2(p)={s5(0.2),s7(0.4),s7(0.4)};

L3(p)={s1(0.2),s6(0.4),s8(0.4)};L4(p)={s3(0.2),s3(0.4),s7(0.4)}.

由上式计算得:dnhd(L1(p),L2(p))= 0.36,dnhd(L1(p),L3(p))= 0.36,dnhd(L1(p),L4(p))= 0.16,dnhd(L2(p),L3(p))= 0.16,dnhd(L2(p),L4(p))= 0.20,dnhd(L3(p),L4(p))= 0.20.由以上结果可以看出,利用上述公式计算任意两个PLTSs之间的距离时具有一定的缺陷性,即有时难以准确区分出任意两个概率语言术语集之间的距离.

方法2利用定义6中的距离公式计算例3.将公式中的λ和ω分别设为1、1/2,于是由此直接进行计算得:dnhd(L1(p),L2(p))=0.36,dnhd(L1(p),L3(p))=0.32,dnhd(L1(p),L4(p))=0.16,dnhd(L2(p),L3(p))= 0.144,dnhd(L2(p),L4(p))= 0.216,dnhd(L3(p),L4(p))= 0.208.由上述结果可以看出,定义6中的距离测度能有效克服文献[10]中距离测度所存在的不足.

3 实际应用

为了证实本文提出的距离公式的合理性和有效性,本文采用TOPSIS方法对文献[11]中的例子进行分析.该实例解决的是可信网络社团扩张的问题,即:在新节点{x1,x2,x3,x4}中选择出最优的一个节点加入社团.对新节点进行综合评判的属性标准为态度、行为、意志、诚信、责任,其中属性评价的语言术语集为S={s0,s1,s2,s3,s4}.专家基于各个标准对每个节点进行评价的结果见表1.

表1 概率语言决策矩阵

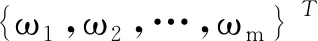
步骤1根据专家提供的决策信息构造决策矩阵,结果如表1所示.

步骤2 确定PLTSs的正、负理想解[12].

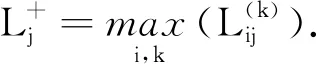
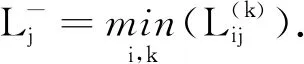
由以上可得PLTSs的正、负理想解分别为:x+=(s4(1),s4(1),s4(1),s4(1),s4(1)),x-=(s1(1),s1(1),s2(1),s1(1),s2(1)).

步骤3 确定各个属性的权重.首先在式(5)中分别取ω为0.1、0.2、…、0.9来计算表1中的各PLTSs的熵测度.计算结果显示,利用不同ω值计算得到的熵测度几乎相同,因此本文在此取ω= 0.5对PLTSs进行计算,所得结果为:

步骤4 计算各个备选方案与正、负理想解之间的加权距离,其计算公式为:

dnhd(xi,x+)=ω1dnhd(Li1(p),L1(p)+)+ω2dnhd(Li2(p),L2(p)+)+…+

ωndnhd(Lin(p),Ln(p)+).

(6)

dnhd(xi,x-)=ω1dnhd(Li1(p),L1(p)-)+ω2dnhd(Li2(p),L2(p)-)+…+

ωndnhd(Lin(p),Ln(p)-).

(7)

利用式(6)和式(7)计算得:dnhd(x1,x+)= 0.3605641,dnhd(x2,x+)= 0.1851517,dnhd(x3,x+)=0.3102368,dnhd(x4,x+)= 0.2103486;dnhd(x1,x-)= 0.2856572,dnhd(x2,x-)= 0.4610697,dnhd(x3,x+)= 0.3359845,dnhd(x4,x-)= 0.4358727.

步骤6 根据CI(xi)值的大小进行方案排序.排序结果为x2≻x4≻x3≻x1.

由排序结果可知,最优节点为x2,并且该排序结果与文献[11]的排序结果完全一致,由此表明基于改进距离测度的TOPSIS决策方法是可行的.

4 比较分析

为了进一步验证本文方法的可行性,将本文方法与文献[4]中提出的基于距离测度的TOPSIS方法进行比较分析(仍以文献[11]中例题为例),具体步骤如下:

步骤1 规范化表1中的数据,结果如表2所示.

表2 规范化后的概率语言决策矩阵

步骤2 确定各个属性的权重.为了便于比较分析,将各个属性权重的取值与上述步骤3中的权重取值保持一致,即仍取:ω1= 0.1554,ω2= 0.2001,ω3= 0.1597,ω4= 0.2294,ω5= 0.2554.

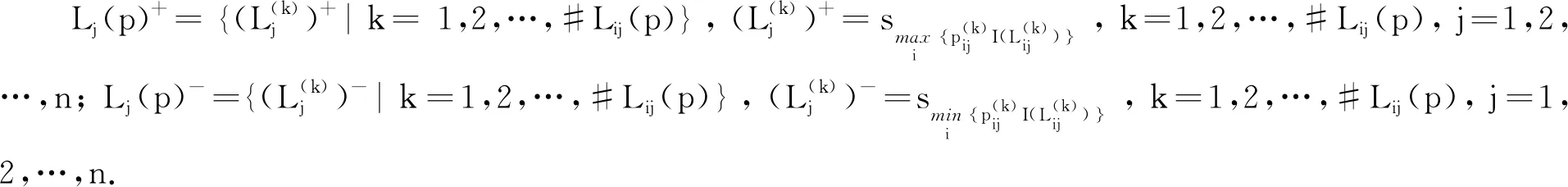
x+=({s2,s1.5,s0.88},{s2.34,s1,s0.46},{s3,s0.88,s0},{s4,s0.78,s0.44},{s3,s1.5,s0.44}),

x-=({s1.04,s0.22,s0},{s1.5,s0.52,s0},{s2,s0,s0},{s1.08,s0,s0},{s2,s0,s0}).

步骤4 计算各个备选方案和正、负理想解之间的偏离度.计算公式为:

由上式可得:d(x1,x+)=0.88,d(x2,x+)=0.56,d(x3,x+)=0.73,d(x4,x+)=0.66,d(x1,x-)= 0.46,d(x2,x-)= 0.78,d(x3,x-)= 0.65,d(x4,x-)= 0.65.

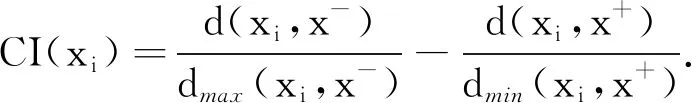
步骤6 根据CI(xi)的值对方案进行排序.排序结果为:x2≻x4≻x3≻x1.

由以上结果可知,利用本文方法得到的最优节点x2不仅与第3部分中所得的最优节点完全一致,而且与文献[4]中的方法(基于传统距离测度的TOPSIS方法)所获得的结果也完全一致.该结果说明,本文提出的基于改进距离测度的TOPSIS方法不仅能有效保留原始的概率语言信息,而且还可有效提高排序的准确度;因此,该方法可为解决模糊多属性决策问题的排序方案提供良好参考.