利用熵权-非整秩次加权秩和比法的铁路规划评价

李子木，唐慧漪，刘晓佳

(集美大学航海学院，福建 厦门 361021)

0 引言

铁路线网规划对于提升城市经济发展水平有重要意义，为构建多地区之间路网完整与城市协同发展提供了强大的支撑。但是，由于相关城市的发展、客运量与政策支持度等因素影响，铁路网中各线路的重要度不尽相同。因此，针对各地区的相关影响因素，对铁路的规划先后顺序进行评估，可以最大化利用建设资源，提高铁路网运行效益。

目前，针对常规铁路相关评价主要通过层次分析法[1]、模糊综合评价法[2-4]、熵权TOPSIS法[5-6]等。但是，层次分析法与模糊综合评价法在建模评价上主观性太强，熵权TOPSIS(优劣解距离法)计算过程较为繁琐，且评价结果较为单一。而本文采用的加权秩和比法(weighted rank sum ratio，WRSR)具有计算过程简单、无量纲要求、综合评估效果优等特点，被广泛应用到医疗卫生领域的质量综合评估及方案选择中[7]。如今，该方法在铁路规划领域研究较少，还未见涉及运用加权秩和比法进行铁路相关评价的研究。因此，本文使用非整秩次加权秩和比方法对铁路线路进行评价。非整秩次秩和比法对编秩方法进行改进，所得指标秩次与原指标值之间存在定量的线性对应关系，避免了指标与秩次转化中原指标值信息的缺失，其结果比秩和比方法更客观。

本文综合考虑规划铁路路网的宏观与微观层面的影响，结合规划铁路路网的影响因素选取评价指标，采用熵权-非整秩次加权秩和比模型对规划路网中的铁路线路进行定量分析与评价，得出铁路线路的建设先后次序及相应的分档情况，并对比分析非整秩次加权秩和比法、传统加权秩和比法与熵权TOPSIS法的评价结果差异，为决策者优化配置建设资源、合理安排建设周期提供参考。

1 非整秩次加权秩和比法

秩和比法是一种具有实际应用价值的综合评价方法，它可以对众多的复杂因素进行定量化分析，对多个研究对象进行评价，并排出优劣顺序，为决策提供依据。本研究选取长三角地区规划中的9条铁路的7项指标，应用秩和比法中的非整秩次秩和比法[8]，科学地评估铁路线路规划的重要度。

1.1 基本原理

首先，根据n个评价对象与m个评价指标构建一个n×m的评价矩阵，将各评价指标得值进行非整秩次转换，获得无量纲统计量；其次，根据各指标的权重，计算WRSR值；最后，运用参数统计分析的概念与方法，计算WRSR值分布，并对研究对象进行排序及分档[9]。

1.2 评级步骤

1.2.1 评价指标矩阵与编秩

1)构建评价矩阵。假设有n条铁路线路，每条线路有m个指标，各指标值记为aij(i=1，2，…，n；j=1，2，…，m)，aij构成矩阵A，即

(1)

2)编秩方法。通过判断各评价指标对于评价结果的影响，确定每个指标属于高优秩指标还是低优秩指标。所编秩次除最小值和最大值为正数外，其余大都为非整数。

传统编秩方法。首先判断指标是高优秩指标还是低优秩指标。对于高优秩指标按照1，2，…，m顺序编秩，若两条线路指标值相同，则取均值作为其秩。而低优秩指标编制顺序与高优秩指标相反。

非整次编秩方法。高优秩指标为

R=1+(N-1)×(X-Xmin)/(Xmax-Xmin)，

(2)

而低优秩指标为

R=1+(N-1)×(Xmax-X)/(Xmax-Xmin)。

(3)

式(2)～式(3)中：R为秩次；N为评价对象数量；X为指标的原始数据，将最大、最小的原始指标值分别记为Xmax、Xmin。

1.2.2 计算WRSR值

记WRSRi为加权秩和比，其计算公式为

(4)

式(4)中：i=1，2，…，n；j=1，2，…，m；Rij为评价对象i的评价指标j的秩次值；Wj为指标的权重值。

1.2.3 确定WRSR分布

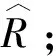
Probit=u(pi)+5。

(5)

其中：u(pi)为离差函数；p(i)为向下累计频率。

1.2.4 计算直线回归方程与分档排序

以Probit为自变量，WRSR值为因变量，利用SPSS 软件求回归方程。依据各分档情況下概率单位Probit值，按照回归方程推算所对应的WRSR估计值对评价对象进行分档排序。

2 权重确定

熵权法是一种客观赋权方法[10]，它弥补了传统专家打分法主观性太强的不足。

2.1 初始矩阵构建

设有n个评价对象，m个评价指标，构建初始矩阵为

(6)

其中：i=1，2，…，n；j=1，2，…，m；yij为第i个评价线路中第j个指标的数值。

2.2 初始矩阵归一化处理

本文采用极差法对数据进行归一化处理，正向指标的具体计算公式为

uij=(max(yj)-yij)/(max(yj)-min(yj))。

(7)

而负向指标的具体计算公式为

uij=(yij-max(yj))/(max(yj)-min(yj))。

(8)

归一化处理后的标准判断矩阵为

(9)

2.3 权重-熵权确定

第i个评价对象中第j个评价指标的特征比重pij为

(10)

第j个评价指标的熵值Ej为

(11)

熵值是不确定性的一种度量，信息量越大，不确定性就越小，熵也就越小；信息量越小，不确定性越大，熵也越大。

第j个评价指标的冗余度Fj为

Fj=1-Ej。

(12)

第j个评价指标的熵权Wj为

(13)

信息量越大，不确定性就越小，熵也就越小，Wj在评价体系中所占的比例越大；信息量越小，不确定性越大，熵也越大，Wj在评价体系中所占的比例越小。

3 实例结果及分析

常规铁路线路规划多侧重于路网经济评价、社会评价及环境评价等方面，每个方面又具有不同的影响因素。在查询大量文献与咨询相关专家的基础上，本文最终选取7个评价指标对长三角地区选定的9条铁路(沪乍杭铁路Y1、沪甬跨海铁路Y2、宁宣黄高速铁路Y3、北沿江高速铁路Y4、杭临绩高速铁路Y5、沪甬舟铁路I段Y6、沪甬舟铁路II段Y7、沪甬舟铁路III段Y8、亳蚌城际铁路Y9)进行评价，这7个评价指标分别是铁路连接度C1、高速公路连接度C2、客运量C3、货运量C4、地区生产总值C5、人均可支配收入C6、政策支持度C7，具体如图1所示。运用本文所提的方法处理参考文献[6]中的数据，确定铁路建设先后的次序与等级，其铁路线路与相关指标信息如表1所示。

依据图 1 的指标，利用熵权法原理求得各项评价指标的权重为W=(0.148，0.145，0.147，0.119，0.145，0.145，0.151)。就指标权重而言，政策支持度、铁路连接度、客运量权重较高，对评价结果影响较大，货运量指标对应权重较小，对评价结果影响较小。利用秩和比法对规划线路进行编秩及加权秩和比的计算结果见表2。

表3 加权秩和比分布

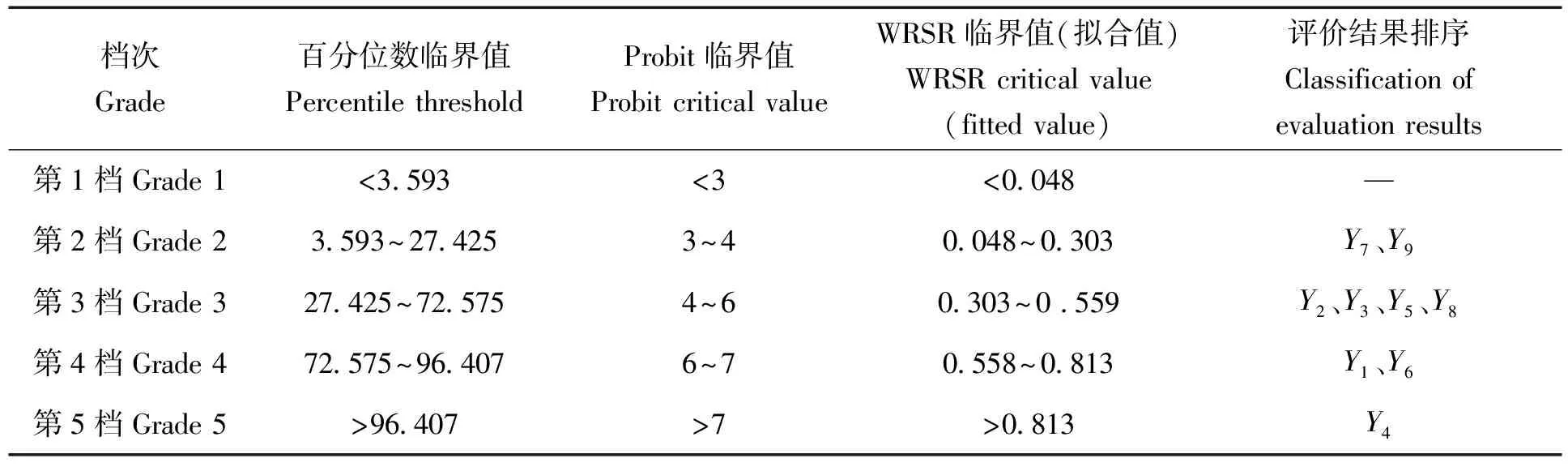
表4 分档数及临界值标准

为了体现评价方法的差异性，整理非整秩次加权秩和比法、传统加权秩和比法、文献[6]中熵权TOPSIS法对于铁路线路的评价结果见表5。

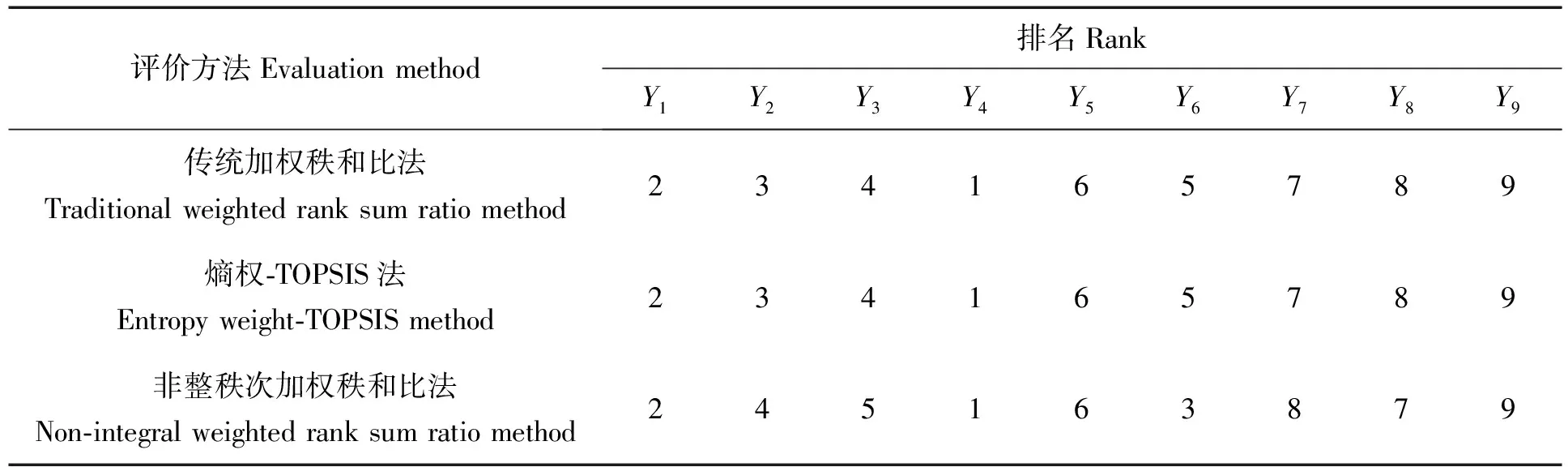
表5 评价方法结果对比

由表5可知，重要度评级最高的铁路线路为线路Y4北沿江高速铁路，重要度评级最低的铁路线路为线路Y9亳蚌城际铁路。

传统加权秩和比法与熵权-TOPSIS法对铁路线路的重要度排序一致，因为在本文传统加权秩和比法与熵权TOPSIS法中权重计算方法一致，均采用熵权法。重要度次序一致也验证了评价结果的有效性与合理性。但是传统加权秩和比法对评价铁路线路进行了重要度分级，更好地获得各线路的重要度等级，相比熵权-TOPSIS法评价优效更充分。

在熵权-TOPSIS法与非整秩次加权秩和比法中，线路Y2、Y3、Y6、Y7、Y8的评价结果前后次序略有不同，主要是因为在熵权法求取权重时，本文是在归一化之后对评价指标求取特征比重，避免了原始数据信息缺失对于权重确定的影响，得到的评价结果更加合理。

由于传统加权秩和比法与非整秩次加权秩和比法对指标的编秩方式存在区别，导致各项指标秩次的位次虽然相同，但秩次值不同，所以RSR值也不同。非整秩次计算方法体现了原始数据顺位间的差距，所以比传统加权秩和比法的评价结果更客观。

综合对比，本文提出的熵权-非整秩次加权秩和比法铁路规划优选模型，其计算过程更加合理、科学，该模型不仅能够简化确定铁路线路规划先后顺序的过程，还能对评估对象进行分层评级，更加直观有效地表现评价结果，可以为决策者统筹规划、合理安排建设顺序提供决策参考。

4 结论

本文运用熵权法确定各指标权重，利用非整秩次加权秩和比法对目标铁路路线进行评价，求得铁路线路施工顺序与重要度等级，以合理配置铁路建设资源。熵权-非整秩次加权秩和比法既能避免主观因素的影响，简便、快速量化各影响指标的权重，又能客观、准确地反映出规划铁路各方面特性，有较强的适应性。另外，后续研究还应进一步考虑相关地区因素对于铁路规划线路的影响。