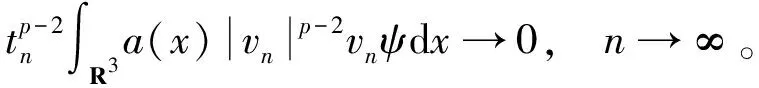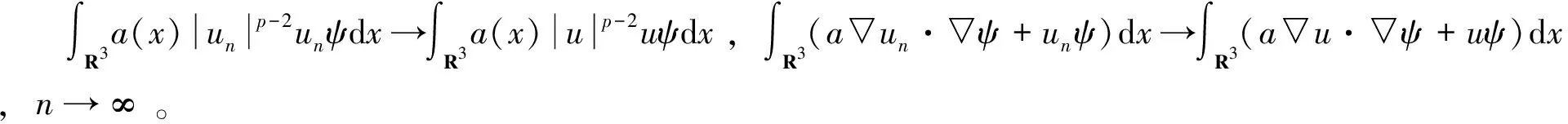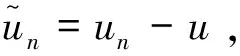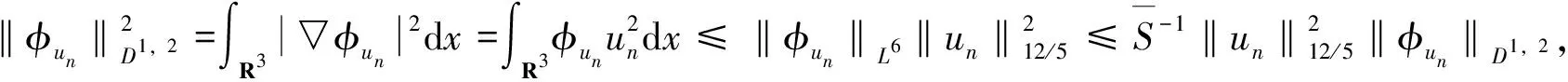一类Kirchhoff-Schrödinger-Poisson方程的非平凡解
2024-01-05蓝永艺
胡 仙,蓝永艺
(集美大学理学院,福建 厦门 361021)
0 引言
近几年来,Schrödinger-Poisson系统
(1)
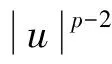
(2)
也开始引起了大家的关注。文献[9]基于一些条件和对L(x)∈L2(R3)的假设条件,证明了其解的存在性与不存在性。当4 本文在文献[11]研究基础上,考虑Kirchhoff-Schrödinger-Poisson方程 (3) 非平凡解的存在性,其中,a>0,λ>0,b≥0,4 定理1 设条件(A1)、(A2)成立且4 (4) 将式(4)代入式(3)的第一个方程可得 (5) 分3步来证明定理1。 第一步,(PS)条件。先证任意的(PS)c序列在H1(R3)中都是有界的,再证I满足(PS)c条件,即任意的(PS)c序列都有收敛子列。 设H1(R3)中序列{un}满足:I(un)有界,且I′(un)收敛于0,即I(un)→c,I′(un)→0。从而对任意的ψ∈H1(R3),都有〈I′(un),ψ〉→0,n→∞。 下面证明{un}在H1(R3)中有界。反证法,假设当n→∞时,tn=‖un‖→∞。令vn=un/tn,那么vn∈H1(R3)且‖vn‖=1。从而存在v∈H1(R3),使得在任意有界区域Ω∈R3上,有 (6) 接下来证v(x)=0在R3。令un=tnvn, (7) 接着证x包含在Ω+和Ω-中。假设条件(A1)和(A2),暗示Ω+≠Ø和Ω-≠Ø。首先考虑x∈Ω+的情况。因为a(x)∈C(R3),这里存在δ>0,有 a(y)>0,任意的y∈Bδ(x)。 (8) (9) (10) 令〈I′(un),ψ〉→0中ψ=vn,并对式(10)两边分别除以tn=vn,可得 (11) 现在证明{un}有收敛子列,依然记为{un}。假设存在u∈H1(R3),使得 (12) 首先令ψ=u,当n足够大时,有 (13) 当n足够大时,可得 (14) (15) (16) 接下来,不失一般性,假设a∞<-1。由条件(A1)可知,存在R0>0,使得a(x)<-1,|x|>R0。又因为a(x)∈C(R3)和4 (17) 因为I(u)=I(|u|)在H1(R3)中,所以可得u≥0在R3,它为问题(3)的解且满足I(u)>0。由强极大值原理可得,u>0在R3中。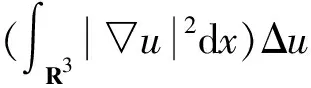

1 预备知识
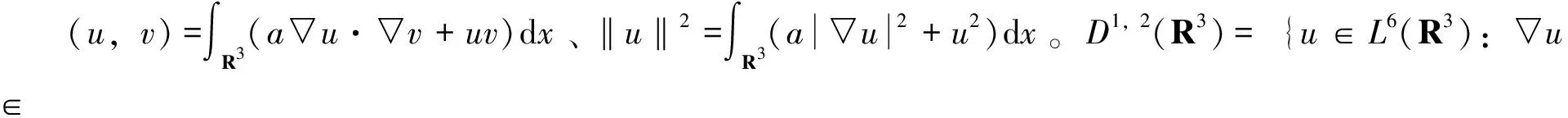
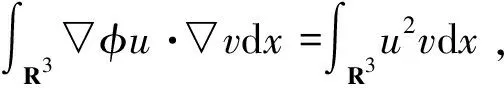

2 定理的证明