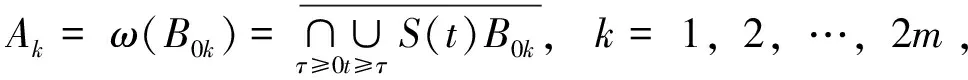具变系数和弱阻尼的非局部高阶波方程的长时间动力学行为
2024-01-05吕鹏辉余莎莎林国广
吕鹏辉,余莎莎,林国广
(1.苏州大学应用技术学院,江苏 苏州 215325;2.苏州工业园区星洋学校,江苏 苏州 215127;3.云南大学数学与统计学院,云南 昆明 650500)
0 引言
设Ω⊂RN是具有光滑边界的有界区域,本文主要研究Ω上具有变系数和弱阻尼非局部高阶波方程的渐近行为,即
(1)

波动方程通常描述弦的振动规律或者波的运动规律,弦的振动和波的运动通常伴随着阻尼和外力,阻尼通常来自于物体内摩擦或者介质摩擦。梁方程作为一类特殊的波动方程,主要描述梁的偏转和实用负载关系,该方程与基础建设如房屋、桥梁、公路、铁路等息息相关。Woinowsky-Krieger[1]于1950年研究了一维问题下梁的振动问题,建立了模型

(2)
式(2)中的非线性部分表示梁的延伸效应。在Ω⊂RN下,式(2)的一般形式为
(3)
近年来,人们致力于式(3)的可展梁或板方程的研究,也得到了该类问题的许多重要结果。Lin等[2]研究了具阻尼项的广义非线性Kirchhoff-Boussinesq方程的整体动力学,得到了该类方程的整体吸引子和指数吸引子;Feng等[3]研究了一类具强阻尼非线性非自治可延伸板方程解的长时间动力学,在初始条件、非线性项和外力项的适当条件下,证明了问题整体解的存在性,并且得到了一致吸引子的存在。更多有关梁板方程的研究可见文献[4-6]。
变系数a(x)表示空间坐标x处的波速,它出现在海洋声学、数学物理等许多领域的波动现象中,因此,研究具变系数的波方程的相关性质具有重要的现实意义。许多学者也研究了具变系数的波动方程的长时间动力学行为,如:Limaco等[7]研究了具有变系数Kirchhoff方程在非线性内阻尼作用下初边值问题强解的整体唯一性及总能量的指数衰减性;Karachalios等[8]研究了半线性双曲方程utt+δut-φ(x)Δu+λf(u)=η(x)的柯西问题,它克服了无界域中算子非紧性带来的困难,并且得到了解的局部存在性和整体吸引子的存在性。更多有关具变系数的波方程研究可见文献[9-11]。
随着研究的深入,学者开始研究高阶波动方程的长时间动力学行为。Messaoudia等[12]研究了具有Dirichlet边界条件的多维高阶Kirchhoff方程,估计了正初始能量下解爆破。林国广等[13]研究了一类非线性非局部且具强阻尼项的高阶Kirchhoff方程的初边值问题,得到了该类高阶方程的整体解的存在唯一性。更多关于高阶Kirchhoff方程的相关研究可见文献[14-16]。
目前,对于具变系数的高阶波方程的渐近行为研究较少,主要遇到的困难是在求解问题时,变系数的处理方式不同。当a(x)是正常数时,作为ut的阻尼系数,此时在做内积过程时,可直接提到内积外面;当a(x)是变系数函数时,a(x)ut与(-Δ)kv(k=1,2,…,2m)做内积,将不能直接把a(x)提出,此时如何处理变系数将成为得到渐近紧的关键。本文运用合理的假设和莱布尼兹公式,灵活处理了变系数带来的耗散估计问题,克服了变系数带来的困难,进而得到有界吸收集和渐近紧性,最后得到问题的整体吸引子族。
1 预备知识
本节主要给出动力系统和整体吸引子(族)的相关理论。
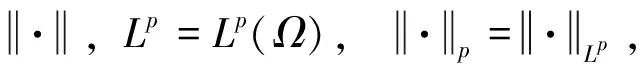
定义1[13]设X是完备度量空间,S(t):X→X(t∈R+)是连续算子族,若对任意s,t∈R+,S(t)满足S(0)=I、S(t+s)=S(t)S(s),则称{S(t)}t≥0是X上的算子半群,(S(t),X)构成连续动力系统,X称为该动力系统的相空间。
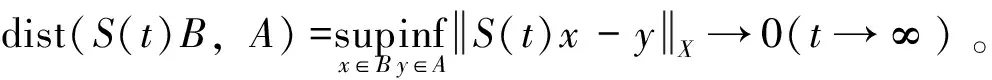
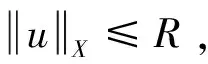
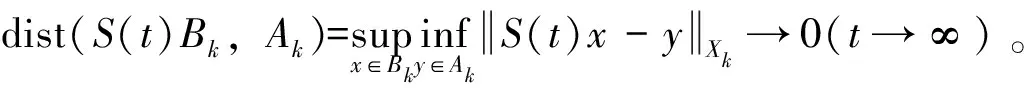

2 整体解的存在性
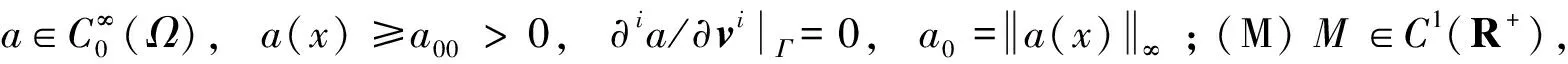
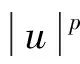
(4)
ug(x,u)-β2G(x,u)≥Φ2(x),Φ2∈L1(Ω),
(5)

(6)
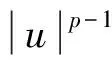
(7)
(8)

(9)
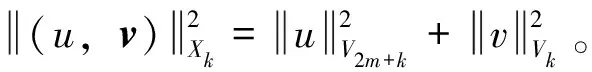
设ε>0足够小,且满足
(10)
引理3 设条件(H)成立,M满足条件(M),f∈H,式(4)~式(8)成立,(u,u1)∈X0,由问题(1)确定的(u,v)满足
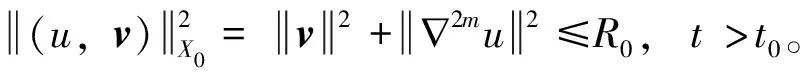
证明将v与方程组(1)在L2(Ω)中作内积,得
(11)
分别处理式(11)中各项得
ε(a(x)u,v)=ε(a(x)u,ut+εu)=(ε/2)d(a(x)u,u)/dt+ε2(a(x)u,u),
(12)
(13)
(14)
(15)
(16)
(17)
将式(12)~式(17)代入式(11)中,得到
(18)
根据假设(H)、(M)和式(5),得
(19)
(20)
(21)
由式(10)及式(19)~式(21),取σ1=min{7a00/4-2ε,ε,2εβ2},则式(18)化为
(22)
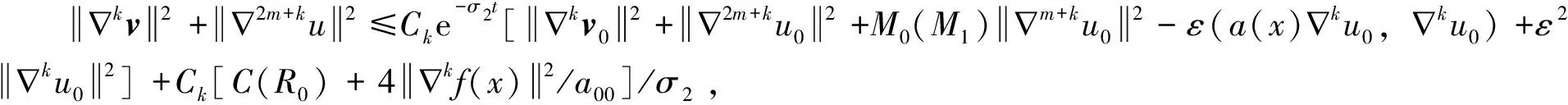
证明将(-Δ)kv(k=1,2,…,2m)与方程组(1)在L2(Ω)中做内积,得
(23)
分别处理式(23)各项得
(24)
(25)
(26)
(27)
(28)
(29)
(30)

(31)
(32)
结合式(23)~式(32)得到
(33)

引理5(整体解的存在唯一性) 在引理3、引理4假设条件下,(u,u1)∈Xk,k=0,1,…,2m,则初边值问题(1)存在唯一的整体解(u,v)∈L∞([0,+∞);Xk)。
证明1)解的存在性。利用Galerkin方法证明整体解的存在性。
(34)
确定,满足初始条件un(0)=un0,unt(0)=un1。当n→+∞时,在Xk中(un0,un1)→(u0,u1),由常微分方程的基本理论可知,近似解un(t)在(0,tn)存在。

第三步,极限过程。在Xk(k=0,1,…,2m)空间中,从序列un中选取子列,任用un表示,则
(un,vn)→(u,v)
(35)

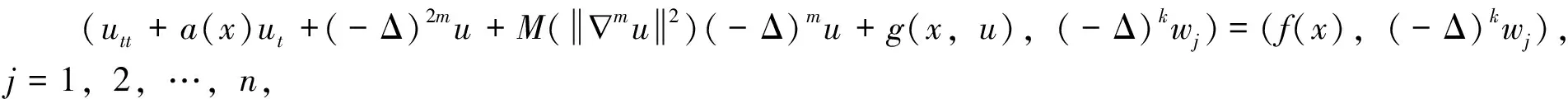
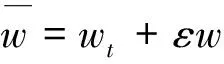
(36)
类似于引理3、引理4处理方法,得
(37)
(38)
(39)
(40)
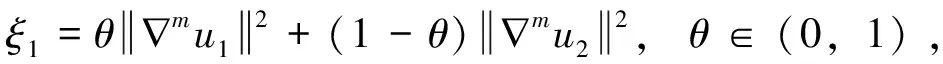
(41)
其中,ξ2=θu1+(1-θ)u2,θ∈(0,1)。

(42)
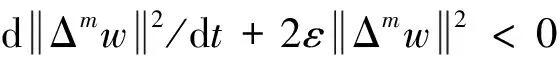
(43)
3 整体吸引子族的存在性