时间分数阶Klein-Gordon方程的有限差分方法
2024-01-05梁宗旗
丁 鹏,梁宗旗
(集美大学理学院,福建 厦门361021)
0 引言
近年来,由于分数阶微积分的不断发展,分数阶微分方程在科学与工程的各个领域都得到了广泛的应用,如光学[1]、流体力学[2]、化学[3]、物理学[4]、金融[5]和其他自然科学[6]。在分数阶微分方程理论分析上,已经有大量学者开展了许多重要的工作[6-14]。但是,大多数分数阶微分方程的精确解依然难以直接给出,即使是含有特殊函数的线性分数阶微分方程亦是如此。由于这些特殊函数大多是无穷级数,其收敛速度比较慢,导致这些函数的计算也变得相当困难。因此,分数阶偏微分方程的数值求解成为当今相关研究领域的课题之一。
本文研究了时间分数阶Klein-Gordon方程
(1)
u(x,0)=φ(x),ut(x,0)=ψ(x),x∈[-L,L],
(2)
u(-L,t)=0,u(L,t)=0,t∈(0,T]。
(3)
其中:f(x,t)为已知函数;φ(x)、ψ(x)为初值函数。Caputo分数阶导数为
(4)
关于时间α(0<α≤1)阶偏微分方程的数值解法,已经有丰富的研究成果,但相对时间α(1<α≤2)阶偏微分方程而言,其数值求解的研究成果比较欠缺。Zhang等[12]将时空分数阶非线性Klein-Gordon方程进行有限差分L1格式离散,空间上进行谱离散,利用线性化的方法将非线性项线性化,并利用能量法证明其离散格式是无条件稳定的。Vong等通过构造一维和二维时间分数阶Klein-Gordon方程的空间紧差分格式,得到空间上4阶的收敛阶,并利用能量法证明了其收敛性和稳定性[15-16]。Chen等[17]利用时空谱方法求解了时间分数阶非线性Klein-Gordon方程的数值解,并证明了其离散格式的收敛性和稳定性。事实证明,关于差分格式收敛性和稳定性的分析,大都采用能量法证明数值解是有条件或无条件稳定的。Sun等[13]提出了一种新的能量分析方法来分析多项时间分数阶偏微分方程的收敛性与稳定性,给出有关Caputo导数L1差分格式的相关结果,证明了时间分数阶混合次扩散方程和扩散波方程有限差分格式的收敛性与稳定性。事实表明,这种新的能量分析方法也能推广应用到其他时间α(1<α≤2)阶偏微分方程的数值求解问题,分析其有限差分格式的收敛性和稳定性。因此,本文利用这种新的能量分析方法,严格证明时间分数阶Klein-Gordon方程的L1有限差分格式的收敛性与稳定性。
1 时间分数阶Klein-Gordon方程有限差分的构建
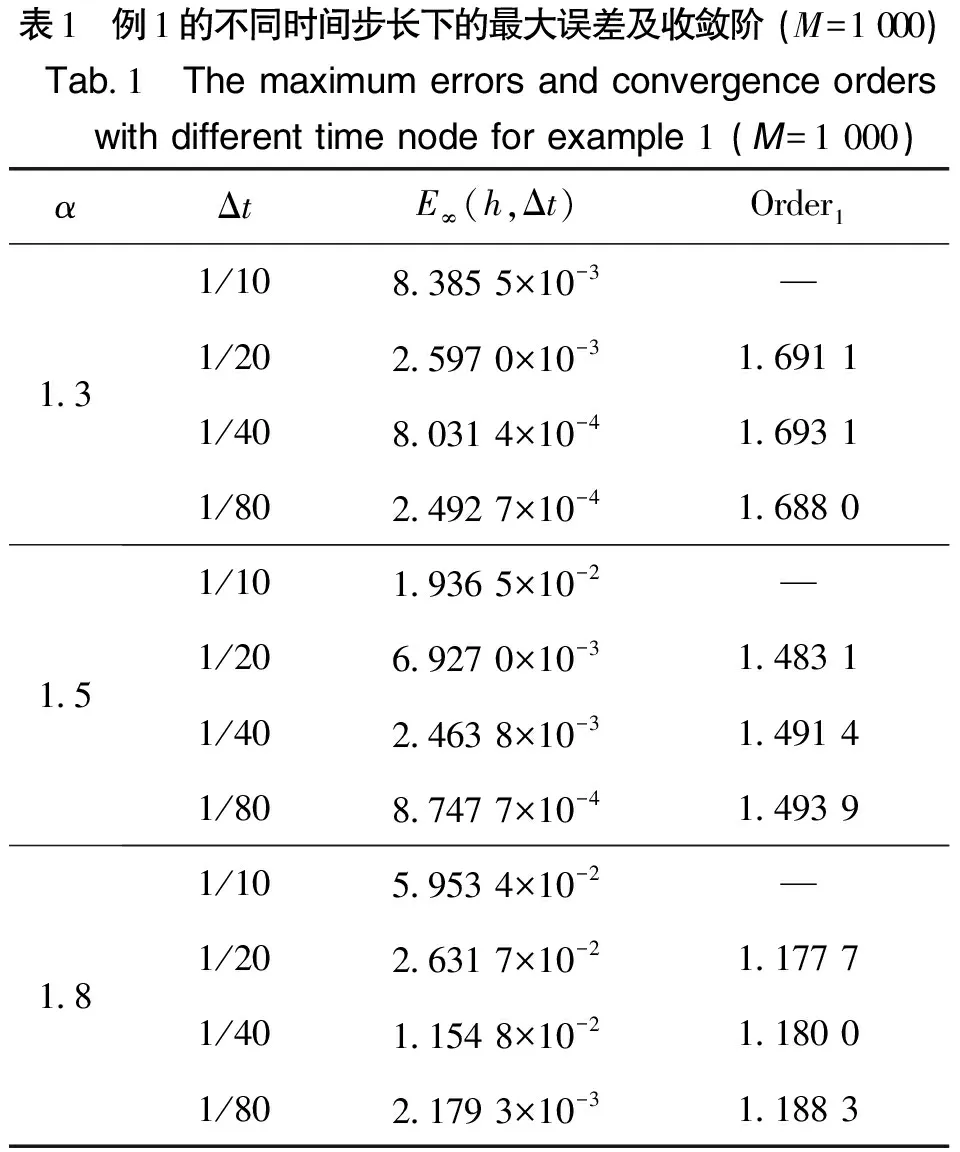
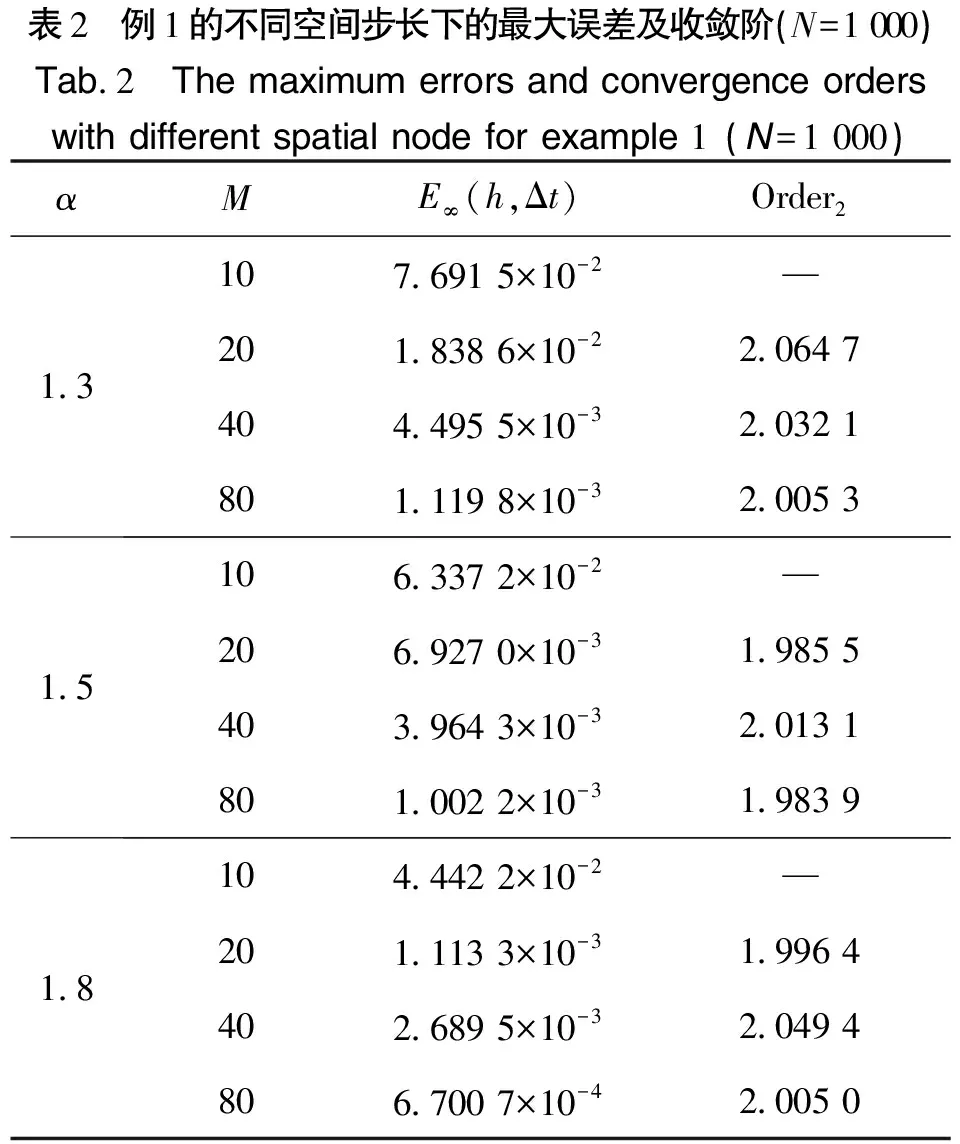
记Λ:=[-L,L],I=(0,T],Ω=Λ×I,将求解区域Ω={(x,t)|-L≤x≤L,0 分别在节点(xi,tn)和(xi,tn-1)考虑方程(1),并相加得到 u(xi,tn-1)]=[f(xi,tn)+f(xi,tn-1)]/2,1≤i≤M-1,1≤n≤N。 对时间Caputo导数采用L1格式逼近,空间导数采用中心差分格式逼近,得到 (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) 式(14)等式右端第一部分和第二部分分别利用分部求和公式,得到 (15) (16) 将式(15)~式(16)代入式(14)中,得到 (17) 式(17)乘以Δt,将n从1到N求和,并利用引理3,得到 (18) 式(18)利用引理2,得到 (19) 利用引理5,式(19)右端最后一项得 (20) 将式(20)代入式(19)中,得到 (21) (22) 式(22)可改写为 (23) (24) 定理1证毕。 类似于定理1的证明,差分格式(11)~(13)有如下的收敛性,即定理2。 证明用式(5)~式(7)减去式(11)-式(13),得到 (25) (26) (27) 表1分别给出了α=1.3、1.5、1.8和Δt=1/10、1/20、1/40、1/80差分格式(11)~(13)的误差和收敛阶。从表1中可以看出,差分格式(11)~(13)在无穷模下的时间方向上收敛阶为3-α。表2给出了α=1.3、1.5、1.8和M=10、20、40、80差分格式(11)~(13)在T=1处的误差和收敛阶,得到无穷模下的空间收敛阶为2。由表1和表2可以看出,差分格式(11)~(13)的收敛速度较快,而且数值结果和理论分析结果是一致的。 表1 例1的不同时间步长下的最大误差及收敛阶 (M=1 000)Tab.1 The maximum errors and convergence orders with different time node for example 1 (M=1 000)αΔtE∞(h,Δt)Order11.31/108.385 5×10-3—1/202.597 0×10-31.691 11/408.031 4×10-41.693 11/802.492 7×10-41.688 01.51/101.936 5×10-2—1/206.927 0×10-31.483 11/402.463 8×10-31.491 41/808.747 7×10-41.493 91.81/105.953 4×10-2—1/202.631 7×10-21.177 71/401.154 8×10-21.180 01/802.179 3×10-31.188 3 表2 例1的不同空间步长下的最大误差及收敛阶(N=1 000)Tab.2 The maximum errors and convergence orders with different spatial node for example 1 (N=1 000)αME∞(h,Δt)Order21.3107.691 5×10-2—201.838 6×10-22.064 7404.495 5×10-32.032 1801.119 8×10-32.005 31.5106.337 2×10-2—206.927 0×10-31.985 5403.964 3×10-32.013 1801.002 2×10-31.983 91.8104.442 2×10-2—201.113 3×10-31.996 4402.689 5×10-32.049 4806.700 7×10-42.005 0 同例1,例2给出了有关时间和空间方向上无穷模下的误差和收敛阶。由表3可以看出,当α=1.3、1.5、1.8、时间步长成1/2倍减少时,差分格式(11)~(13)的时间方向上是3-α阶收敛的。由表4可以看出,当α=1.3、1.5、1.8时差分格式(11)~(13)在无穷模下的空间方向上收敛阶为2。这与定理2中差分格式的收敛阶是O(Δt3-α+h2)是一致的,说明数值结果和理论分析是一致。 表3 例2的不同时间步长下的最大误差及收敛阶(M=1 000)Tab.3 The maximum errors and convergence orders with different time node for example 2 (M=1 000)αΔtE∞(h,Δt)Order11.31/101.112 2×10-1—1/203.448 2×10-21.689 61/401.064 8×10-21.695 21/803.282 7×10-31.697 71.51/102.470 4×10-1—1/208.845 8×10-21.481 71/403.146 9×10-21.491 11/801.115 9×10-21.495 61.81/107.116 8×10-1—1/203.131 2×10-11.184 41/401.371 1×10-11.191 31/805.988 1×10-21.195 2 表4 例2的不同空间步长下的最大误差及收敛阶(N=1 000)Tab.4 The maximum errors and convergence orders with different spatial node for example 2 (N=1 000)αME∞(h,Δt)Order21.3102.949 9×10-2—207.129 2×10-32.048 9401.768 4×10-32.011 3804.435 9×10-41.995 11.5102.543 1×10-2—206.266 0×10-32.021 0401.572 3×10-31.994 7804.073 4×10-41.948 61.8101.913 9×10-2—205.048 4×10-31.922 6401.447 6×10-31.802 2805.453 9×10-41.408 3 本文利用新的能量分析方法,证明了时间分数阶Klein-Gordon方程标准L1差分格式的稳定性与收敛性。数值例子证明,该方法是一个简单、经济和高效的数值方法。下一步的研究将基于L1新的能量分析方法推广应用到其他时间分数阶偏微分方程上,证明其有限差分格式解的稳定性和收敛性。除此之外,还可以建立基于L2新的能量分析法来证明时间分数阶微分方程高阶的差分格式稳定性和收敛性。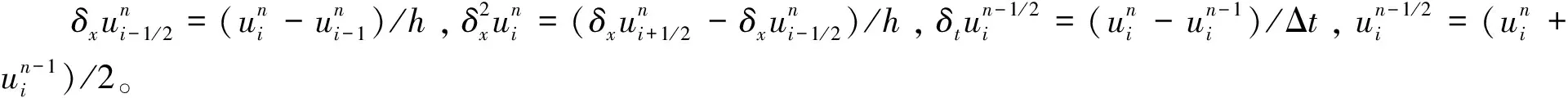
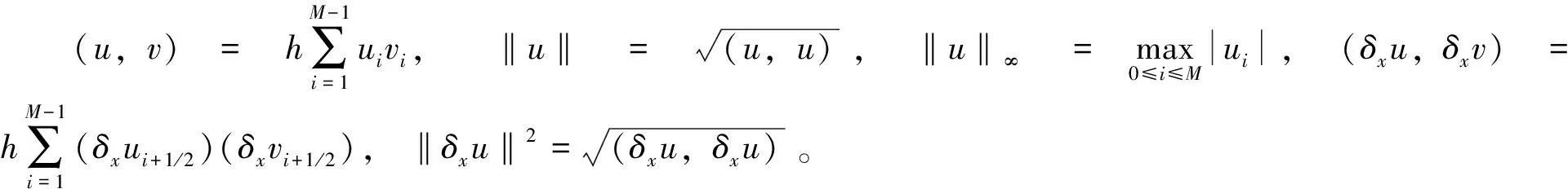
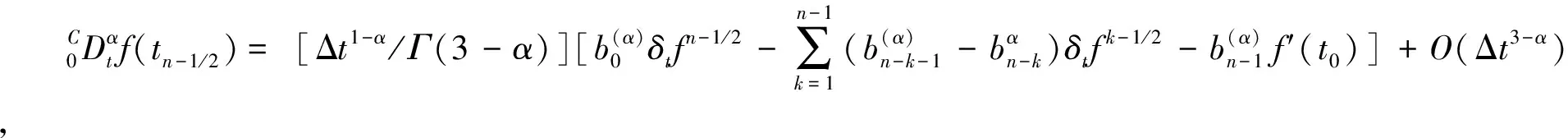
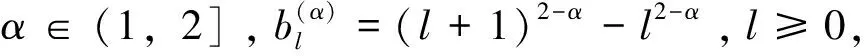
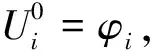
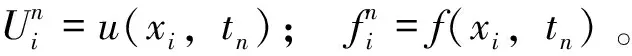
2 收敛性和稳定性分析

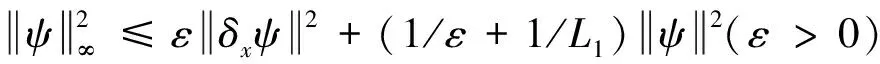



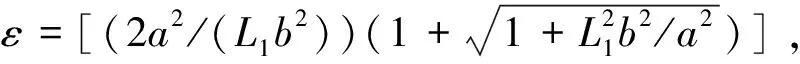
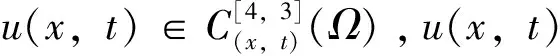
3 数值例子
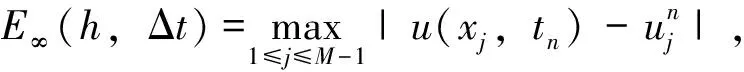
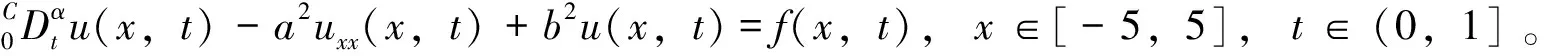
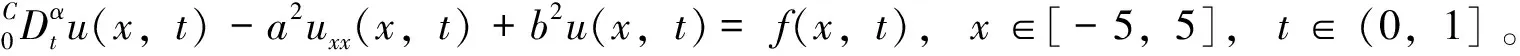


4 结论
