一类离散无向图模型诱导的概念类的样本压缩方案

2024-01-04李本崇郭丰毅

纯粹数学与应用数学 2023年4期

李本崇, 郭丰毅

(西安电子科技大学数学与统计学院, 陕西西安 710126)

1 引言

泛化和压缩是统计学习中的两个重要方面. 泛化是指对现有知识的扩展, 而压缩则强调对知识的简化. 它们紧密相联: 学习算法执行压缩, 而压缩能力保证了良好的泛化性能. 这种联系的一种运用, 正是在统计学习中被广泛遵从的奥卡姆剃刀准则: 如果输入样本可以被压缩为一部分与其保持一致的子样本, 良好的泛化性能就可以得到保证[1].

概念类的样本压缩方案由压缩函数和重构函数两部分组成: 压缩函数能够将有限样本压缩为带标签或无标签的子样本, 而重构函数则能够将这些子样本恢复为与原始样本一致的一个概念. 一个自然的问题是: 是否每个概念类都有一个大小仅依赖于其VC(Vapnik-Chervonenkis)维数的压缩方案?其中VC 维数是函数类复杂性的一个度量[2].文献[3-4] 给出了一个猜想: 每个VC 维数为d的概念类都存在一个大小为O(d) 的样本压缩方案. 这个猜想引发了学者们的系列研究. 文献[3] 为每个概念类C 构建了大小为log ∣C∣的样本压缩方案. 文献[5] 证明了关于样本压缩方案的紧致性定理, 并且还指出对于无限类的压缩方案的存在性是从有限类的存在性中得出的, 因此只需要考虑有限的概念类. 文献[6] 考虑了最大类的一个推广: 极端类(基于三明治定理[7-8]), 并为极端类构建了大小为d的带标签压缩方案. 文献[9] 构造了大小为exp(d) 的样本压缩方案. 对一些自然而重要的概念类, 学者们对其无标签样本压缩方案(压缩函数将给定的样本压缩到样本域的一个子集) 做了积极探索, 取得了显著成果[10-14].

从代数几何学的视角, 一个统计模型是一个实代数簇[15]. 考虑离散模型, 它是一些多项式的解集与概率单形的交集[16-17]. 文献[18] 证明了一般离散无向图模型(非完全图) 诱导的概念类不属于定向拟阵复形的范畴. 对于包含两个顶点X1,X2且无边连的无向图,X1∈{0,1},X2∈{0,1,…,k2-1} (k2∈N,k2≥2). 针对该离散无向图模型诱导的概念类, 文献[18] 给出了一个带标签压缩方案, 但方案是非适当的. 本文考虑这类无向图模型诱导的概念类, 基于文献[19-20] 的工作, 应用模型的二次二项式表示, 构建了大小为其VC 维数的带标签样本压缩方案, 证明了所提方案的适当性.

文章结构安排如下: 第二节介绍文中用到的主要定义和符号; 第三节给出了一类离散无向图模型诱导的概念类的带标签样本压缩方案, 大小为其VC 维数, 并证明了方案是适当的; 第四节总结了本文的工作.

2 预备知识

2.1 概念、概念类、VC 维数

一个概念c是指从域X 映射到{0,1} 的一个函数. 本文假定∣X∣是有限的, 这里∣X∣指X 的基数. 一个概念c也可以看作是X 的一个子集,x∈c当且仅当c(x)=1.一个概念类C 是定义在X 上的一个函数族, 是具有相同域的概念构成的一个集合.

考虑X 的子集A, 类C 在A上的限制是一个概念类C∣A{c∩A∶c∈C}. 如果∣C∣A∣=2∣A∣,则称A被概念类C 打散,其中∣A∣是A的基数. 进一步,概念类C 的VC维数定义为

2.2 离散无向图模型及其代数几何表示

考虑简单无向图. 一个无向图G= (V,E) 包含一个顶点集V和一个无序顶点对的集合E. 如果图G中的任两个顶点之间都存在一条边, 则称图G是完全的.设图G′= (V′,E′), 若V′⊆V且E′⊆E, 则称G′为G的子图. 若子图G′的顶点集V′中任意两个顶点对应原图G中的边均在E′中, 则称G′为图G的导出子图. 给定一个无向图G, 一个团指的是G的一个极大完全导出子图, 用κG来表示G的所有团的集合. 本文中,V={X1,X2,…,Xn}, 每个Xi表示一个离散随机变量,Xi∈[ki]={0,1,…,ki-1},ki∈N 且ki≥2. 进一步, 令X=(X1,X2,…,Xn) 是一个n-维向量, 则样本空间X =[ki].

一个离散无向图模型P是一族离散分布,P中X 上的一个分布P可表示为

其中x=(x1,x2,…,xn)∈X,ψK(x) 是定义在X 上的只通过K中变量取值依赖X 的非负实函数. 本文仅考虑P中正概率分布, 记为P+.

接下来介绍离散无向图模型的代数几何表示. 考虑实多项式环R[X], 它的未定元是初等概率px1x2…xn. 考虑一个子集I⊆R[X], 若满足: (1) 0 ∈I; (2) 如果f,g∈I,则f+g∈I;(3)如果f∈I且h∈R[X],hf∈I;则称它是一个理想.每一个理想I∈R[X]对应一个簇

其中k=ki,是由k维向量组成的集合, 其每一个向量的各分量均为正实数.

给定一个无向图G, 如果(Xi,Xj)∉E, 则称给定{X1,X2,…,Xn}{Xi,Xj} 时Xi与Xj独立, 记为XiXj∣{X1,X2,…,Xn}{Xi,Xj}, 称为一个对条件独立情形. 每一个XiXj∣{X1,X2,…,Xn}{Xi,Xj} 对应二次二项式的一个集合: ∀xi,x′i∈[ki],∀xj,x′j∈[kj], ∀z∈[kl],

记Ipairwise(G)是R[X] 中由所有对条件独立情形对应的二次二项式生成的理想.Hammersley-Clifford 定理表明=P+(见文献[19]).

例2.1图1 中的G1是一个简单无向图, 其中V={X1,X2},κG1={{X1},{X2}},E=∅. 若X1,X2∈[2], 则X 中有四个元素:x(0,0),x(1,1),x(0,1),x(1,0).

由于X1X2, 该离散无向图模型对应的二次二项式的集合为

2.3 离散无向图模型诱导的概念类

首先定义符号函数

其中x∈R. 给定一个离散无向图模型, 其诱导的概念类C 为X 上的二值函数构成的集合, 即

考虑无向图G1, 不存在一对概率分布P,Q∈P+使得

取值为(1,1,0,0) 或(0,0,1,1). 由于

(0,0,0,0) 也不可能出现.

例2.2上例中, 离散无向图模型诱导的概念类C1如图2 所示, VCdim(C1)=3(见文献[20]).

图2 一个概念类C1

2.4 带标签样本压缩方案

一个带标签的样本是一个集合S= {(x(1),y(1)),…,(x(m),y(m))}, 其中x(i)∈X,y(i)∈{0,1}. 概念类C 的一个带标签样本压缩方案由一个压缩函数g和一个重构函数h组成, 函数g将一个来自C 中某个概念的样本映射到一个带标签的子样本, 即压缩集. 函数h将子样本映射到X 上的一个与原始样本一致的概念. 如果对于任何样本S,有h(g(S))∈C, 则称此压缩方案是适当的, 否则称为不适当的.

3 主要结果

考虑图1 中的无向图G1, 若X1∈[2],X2∈[k2] (k2∈N,k2>2), 该离散无向图模型对应() 个二次二项式

其中j,k∈[k2],j2 时可能存在(0,0,0,0)的情况,即k2>2 时最多有14 种情况,记为C2,其中VCdim(C2)=k2+1(见文献[20]).

考虑(1) 式, 已知px(0,j),px(1,k),px(0,k),px(1,j)中的任意三个数值时, 即可得另一个概率值. 若已知{(x(0,j),0),(x(1,k),0),(x(1,j),1)},x(0,k)的标签必为0, 否则会出现(0,0,1,1) 的情况. 同理, 若已知

必分别重构为 (0,0,1,0), (0,1,0,0), (1,0,0,0), (1,1,0,1), (1,1,1,0), (0,1,1,1),(1,0,1,1). 这8 种情况, 每种对应一个大小为3 的带标签压缩集, 记为Part 1, 其中Part 1 对应的带标签压缩集构成的集合记为L1. 剩余的6 种情况, 每种对应四个大小为3 的压缩集, 此部分记为Part 2, 其中Part 2 对应的压缩集构成的集合记为L2. C2的一个压缩方案如表1 所示, 这里x(1),x(2),x(3),x(4)代表x(0,j),x(1,k),x(0,k),x(1,j).

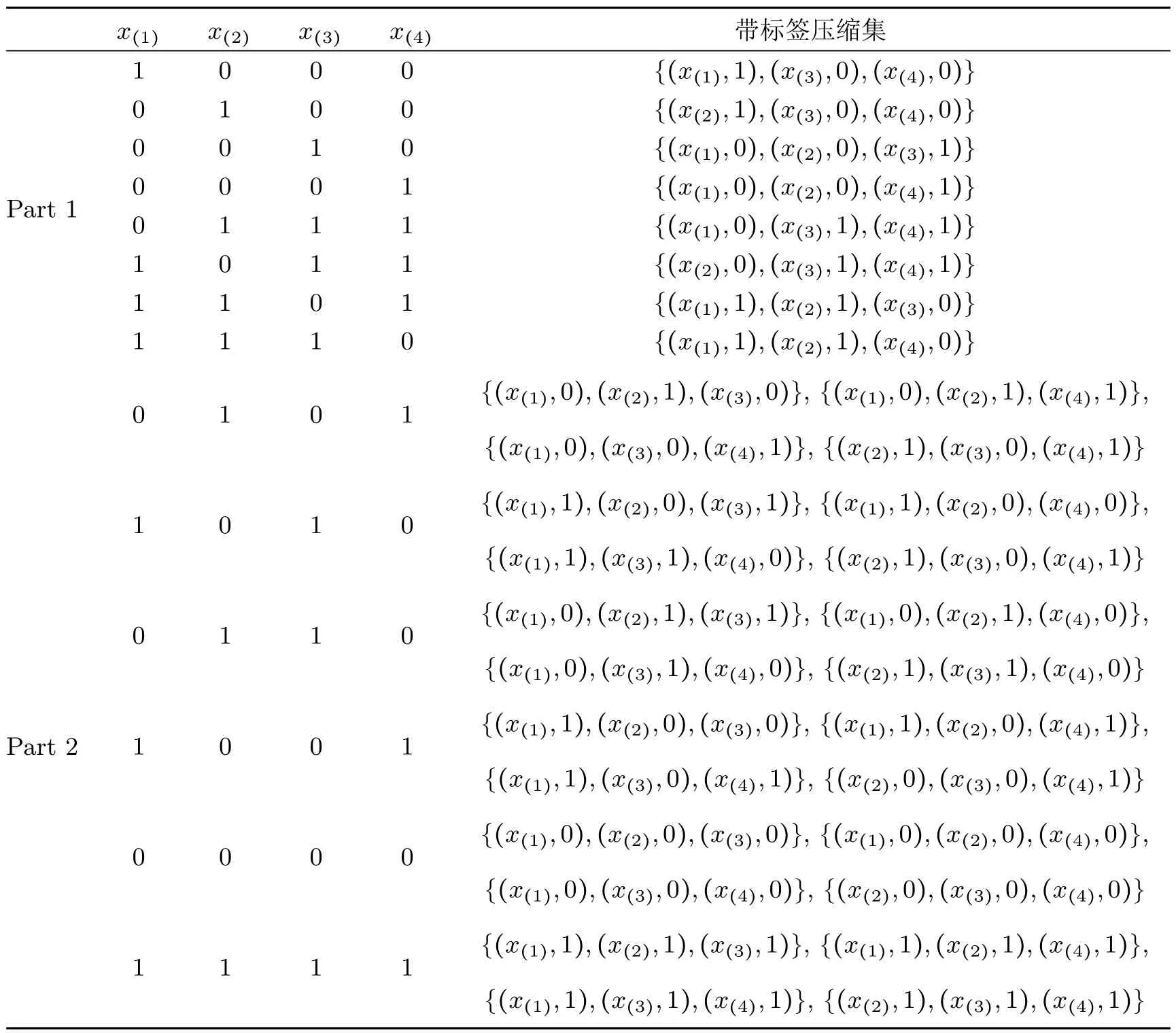
表1 C2 的一个带标签压缩方案

用B1,B2,…,Bn分别记2k2个域点需要满足的每个二次二项式对应的域集, 其中n=(), 考虑样本S(∣S∣≥k2+1) 来自于C2中的某个概念c. 基于表1, 下面给出C2的带标签压缩方案.

带标签压缩方案:

(1)压缩算法: 输入样本S. 在样本中选定一对样本点{(x(0,i),y(0,i)),(x(1,i),y(1,i))}(选择时优先考虑满足(y(0,i),y(1,i))=(0,1) 或(1,0) 的点). 令

若B′≠∅, 则依据压缩方案Part 1, 从B′的每个元素中移除一个相应样本点, 剩余样本点的集合记为D. 再令

如果D′≠∅, 保留样本点{(x(0,i),y(0,i)),(x(1,i),y(1,i))}, 利用压缩方案Part 2 从D′的每个元素中移除一个样本点, 将保留的样本点记为s并输出.

(2) 重构算法: 输入一个大小至多为k2+1 的子样本s. 在子样本中选定一对样本点{(x(0,i),y(0,i)),(x(1,i),y(1,i))} (优先选择(y(0,i),y(1,i))=(0,1) 或(1,0) 的点). 令

若B′′≠∅, 则可通过L2重构出每个Bt中的未知样本点. 其余的未知样本点可利用L1重构(使用{(x(0,i),y(0,i)),(x(1,i),y(1,i))} 对应的二次二项式). 若y(0,j),y(1,j)标签未知, 任意补充y(0,j)或y(1,j)的值, 通过样本点{(x(0,i),y(0,i)),(x(1,i),y(1,i))} 和补充点对应的二次二项式预测相应未知样本点. 输出重构出的概念.

下面证明本文构建方案的正确性. 首先说明所构建的算法产生了一个大小至多为k2+1 的压缩集, 且由该压缩集重构出的概念与样本S是一致的.

定理3.1输入一个样本S, 该方案输出一个大小至多为k2+1 的压缩集s, 重构出的概念与原始样本S是一致的.

证明由于∣S∣≥k2+1, 至少存在一对样本点{(x(0,i),y(0,i)),(x(1,i),y(1,i))} 在样本S中, 其中i∈{0,…,k2-1}. (y(0,i),y(1,i)) 的取值有以下三种情形.

情形1: ∃i∈{0,…,k2-1}, (y(0,i),y(1,i))=(1,0).

考虑样本点{(x(0,j),y(0,j)),(x(1,j),y(1,j))},其中j∈{0,…,k2-1},j≠i,(y(0,j),y(1,j))有三种可能的情况: (y(0,j),y(1,j)) = (1,1) 时, 由压缩算法可得样本点(x(0,j),1)被移除; (y(0,j),y(1,j)) = (0,0) 时, (x(1,j),0) 被移除; (y(0,j),y(1,j)) = (1,0) 时, 样本点{(x(0,j),1),(x(1,j),0)} 中任意一个可被移除. 即得∣s∣≤k2+1.

情形2: ∃i∈{0,…,k2-1}, (y(0,i),y(1,i))=(0,1). 与情形1 类似, 通过压缩算法可得∣s∣≤k2+1.

情形3: ∀i∈{0,…,k2-1}, 有y(0,i)=y(1,i)= 0 或y(0,i)=y(1,i)= 1. 然后可由方案Part 2 输出压缩集s, ∣s∣≤k2+1.

综上所述, 压缩算法可产生一个大小至多为k2+1 的压缩集s. 下面考虑重构. 若∣s∣

情形1: (y(0,i),y(1,i))=(1,0). 当y(0,j)=1 时,由压缩方案可得y(1,j)=0;当y(0,j)=0时, 由压缩方案可得y(1,j)=0; 当y(1,j)=1 时,y(0,j)=1; 当y(0,j)=0 时,y(1,j)=1. 同理,(y(0,i),y(1,i))=(0,1) 时也可预测出相应的样本点.

情形2: (y(0,i),y(1,i))=(0,0). 当y(0,j)=1 时, 由压缩方案可得y(1,j)=1; 当y(0,j)=0时, 由压缩方案可得y(1,j)=0; 当y(1,j)=1 时,y(0,j)=1; 当y(0,j)=0 时,y(1,j)=0. 同理,(y(0,i),y(1,i))=(1,1) 时也可预测出相应的样本点.

若子样本s提供的信息不足以重构为某个概念, 则需要补充一些样本点, 此时重构出的概念属于概念类C2吗？

定理3.2对于图1 的无向图G1,X1∈[2],X2∈[k2], 压缩方案重构出来的概念都属于概念类C2.

证明由定理3.1 中重构的证明可知, 通过方案重构出的任一概念对应的二次二项式中(x(0,j),x(1,k),x(0,k),x(1,j)) 对应标签不存在(0,0,1,1) 或(1,1,0,0) 的情况. 要证方案重构出的概念属于C2, 即证存在一对分布P,Q对应此概念. 概念类C2有2k2个域点, 记为x(0,0),x(1,0),…,x(1,k2-1). 下面分情况讨论域点对应的标签.

情形1: ∀i∈{0,…,k2-1}, 有(y(0,i),y(1,i))=(1,1). 此时P和Q满足条件P=Q即可得到相应概念.

情形2: ∀i,j∈{0,…,k2-1}, 有(y(0,i),y(1,i))=(1,1), (y(0,j),y(1,j))=(0,0).

当k2=2 时, 至少存在

使得

例如

当k2> 2 时, 记{0,…,k2-1} 中满足(y(0,i),y(1,i)) = (1,1) 的个数为m, 满足(y(0,j),y(1,j))=(0,0) 的个数为n,m+n=k2. 将(p(0,0),p(1,0),q(0,0),q(1,0)) 同时除以m, 并将这m对值对应至域{(x(0,i),x(1,i))} 上, 此时有

同理,将(p(0,1),p(1,1),q(0,1),q(1,1))同时除以n,并将这n对值对应至域{(x(0,j),x(1,j))}上. 即得到相应的概念.

情形3: ∀i,j∈{0,…,k2-1}, 有

由情形2 保证存在相应的概念.

情形4: ∀i,j,l∈{0,…,k2-1}, 有

当k2=3 时, 至少存在一对

使得

例如

当k2>3 时,记0,…,k2-1 中满足(y(0,i),y(1,i))=(1,1)的个数为m,(y(0,j),y(1,j))=(0,0) 的个数为n, (y(0,l),y(1,l)) = (1,0) 的个数为v,m+n+v=k2. 类似情形2 中的做法, (p(0,0),p(1,0),q(0,0),q(1,0)) 同时除以m; (p(0,1),p(1,1),q(0,1),q(1,1)) 同时除以n;(p(0,2),p(1,2),q(0,2),q(1,2)) 同时除以v, 将这些比值对应到相应的域上, 即可得到相应的概念.

情形5: ∀i,j,l∈{0,…,k2-1}, 有

由情形4 保证存在相应的概念.

综上所述, 重构出的概念都在概念类C2中, 所提的压缩方案是适当的.

下面看一个例子.

例3.1X1∈[2],X2∈[3], 令C3表示该离散无向图模型诱导的概念类, 则它的域为{x(0,0),x(1,0),x(0,1),x(1,1),x(0,2),x(1,2)}. 对应的二次二项式为:

(1)px(0,0)⋅px(1,1)-px(0,1)⋅px(1,0),

(2)px(0,0)⋅px(1,2)-px(0,2)⋅px(1,0),

(3)px(0,1)⋅px(1,2)-px(0,2)⋅px(1,1).

C3的VC 维数是4[20]. 若样本

它是C3的一个概念, 例如

利用压缩算法移除样本点(x(1,1),0), (x(1,2),0) 得到压缩集

重构时, 通过二次二项式(1) 预测x(1,1)的标签为1; 通过二次二项式(2) 预测x(1,2)的标签为0. 即精确恢复S1.

若样本S2={(x(0,0),1),(x(1,0),0),(x(1,1),0),(x(1,2),0)}, 由算法知S2本身就是一个压缩集. 重构时, 通过二次二项式(1) 预测x(0,1)的标签为1; 通过二次二项式(2) 预测x(0,2)的标签为1. 输出的概念为

此概念属于C3, 例如

若样本S3= {(x(0,0),1),(x(1,0),0)}, 此时可补充x(0,1)的标签为0;x(0,2)的标签为1. 重构时, 通过二次二项式(1) 预测x(1,1)的标签为0; 通过二次二项式(2) 预测x(1,2)的标签为0. 输出的概念为

此概念属于C3, 例如

由定理3.1, 可得如下结论成立.

定理3.3对于图3 中的无向图,令X1∈[2],Xi∈[ki],C4表示该离散无向图模型诱导的概念类, 其中ki∈N,ki≥2,i=2,3. 则C4存在一个大小为k2(k3+1)的带标签样本压缩方案. 进一步, 对于任意包含两个团K1={X1,X2,…,Xn1},K2={X2,X3,…,Xn}且X1∈[2] 的无向图, 对应的离散无向图模型诱导的概念类存在一个大小为VC 维数的样本压缩方案.