谈初中数学建模的基本类型和应用

林沁瑶

数学建模是指根据实际建立数学模型，对数学模型进行分析和求解，以解决实际问题。数学建模是全面提升数学核心素养、推进中学数学素质教育的重要组成部分。提高学生的数学建模能力是落实数学核心素养的根本途径和要求。教师应从引导学生建立数学模型解决实际问题出发，培养学生数学建模思想，让学生深入认识数学学科的特点，真正意识到数学来源于生活又应用于生活。

一、建立二次函数模型解决实际问题

新课标要求会用适当的函数表示和刻画一些实际问题中变量与变量之间的关系，初步预测变量的变化规律，从而用函数来解决简单的实际问题。学生在初中阶段学习了一次函数、反比例函数和二次函数后，意识中有了这些基本函数的模型。因此，面对一些实际问题就可以引导学生尝试通过建立函数模型来解决。

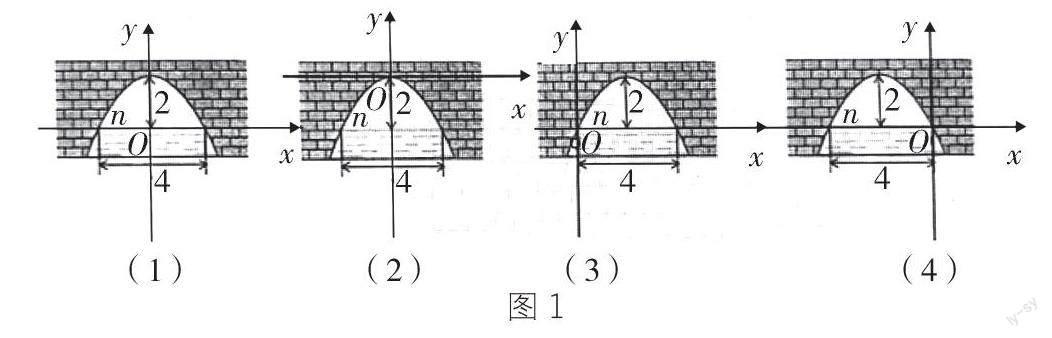
例：潮州西湖里有一条形如抛物线的小拱桥，如图1，当湖面在如图所示的n位置时，拱桥顶（弧的中点）离湖面为2 m ，湖面宽 4 m；当湖面比原来下降 1 m时，问此时水面宽度为多少？水面宽度增加多少 ？

本题是考查以函数为背景的函数型数学模型的问题，学生要解决此问题，首先就要建立函数模型把实际问题转化为函数问题。难点在于如何分析判断这是学过的哪种基本函数模型。从题目中的“抛物线”不难联想到二次函数图像的形状，因此，可以利用二次函数相关的知识解决此问题。由于图像是建立在坐标系中研究的，所以建立适当的平面直角坐标系是解答本题的关键（图1展示了四种不同的建立坐标系模型），再根据函数图像的特征设函数的解析式，并求出相应的二次函数的解析式，进而解决问题。

二、建立几何模型解决实际问题

初中几何图形的学习有很多是三角形、四边形和圆等几何图形的推理证明。几何中的数学建模就是根据几何的基本图形构造模型，需要较强的图形构造能力和空间想象能力。

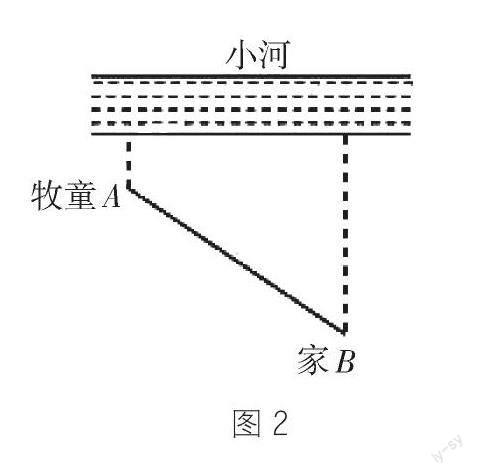
例：如图2，一个牧童在距小河边1千米的点A处放牛，河边同侧且距河边7千米的点B处为牧童的家。已知点A与点B的直线距离是10千米，牧童想先把牛牵到河边去饮水，然后再回家，求牧童要完成这件事情所走的最短路程是多少。

如果“河边”用一条直线l表示，“牧童”用点A表示，“家”用点B表示，那么问题就转化为学生熟悉的几何模型——在直线l上找一个点P，使线段AP与PB之和为最小的数学问题。因此，利用两点关于某条直线对称的性质和勾股定理的知识可以解决。

本题以实际应用问题为背景，从“最短路程”问题中挖掘隐藏着的距离和最值的问题。学生必须以两点关于直线对称的性质为载体，将实际问题转化为距离和最小模型，即两边之和的最小值问题。因三角形A′BA不是直角三角形（如图3），可以进一步构造直角三角形，将问题转化为已知直角三角形两边的长求第三边的基本类型题。把实际问题转化成若干个数学问题就是建模的思想，有利于培养学生的转化思想，从而使思维更具灵活性、创造性。

三、建立概率与统计模型解决实际问题

为满足时代的发展，概率与统计在日常生活中的应用越来越广泛。数学教学应该服务于生活，应注重引导学生将所学概率与统计的知识应用于日常生活等方面，使新课标中提到的“用样本估计总体”数学模型得到更充分地体现。

例：为了估计某一池塘的螃蟹数量，经常采用“抓、放、抓”的方法，即先抓上来n只螃蟹，分别打上标记，再放回去；如果在多次捕获的螃蟹中，每a只中有b只有标记，则尝试估算该池塘的螃蟹数量（用包含b、n、a的代数式表示）。

平时用样本估计总体的试验中，更多的是利用摸球的方式进行试验。对于此种实际问题，学生较为生疏。教学中，教师可以通过平时学生最为熟悉的“摸球问题”进行类比，从而建立数学模型。

１.先从池塘中捉n只螃蟹，做好标记后，重新放回池塘，存在有标记和无标记两种螃蟹——相当于在袋子中放有红和白两种球。

２.让带有标记的螃蟹完全混合于池塘——相当于把两种球搅拌均匀。

３.再捕上来a只螃蟹——相当于在袋子中取出若干球作为样本。

4.发现带有标记的螃蟹只有b只——相当于取出样本中红色球的数目。

5. 样本中有记号的螃蟹的百分比——相当于样本中红色球的百分比。

6. 估计池塘中有记号的螃蟹的百分比——相当于估计总体红色球的百分比。

因此，此题可解答为：设该池塘中有螃蟹x只，则＝，解得x＝。

本题用生活中可能碰到的实际问題，提出了如何估计池塘中螃蟹的数量，激发了学生解决问题的欲望和学习的兴趣。在解决此问题时，重在指导学生类比熟悉的模型，把未知关系转为已知的关系，还可以先用数字表示，再到用字母代替数字，让学生获得对数学知识的理解与认同并掌握用样本估计总体的数学模建，为以后解决新的问题打好基础。

四、建立方程（组）模型解决实际问题

方程模型的题型有工程、增长率、利息和税率、面积、分配等问题。解决此类型题，通常从分析问题的数量关系入手，设定未知数，运用定义、性质、定理、公式和已知条件、隐含条件，把实际问题中已知量和未知量之间的数量关系，转化为方程（组）的数学模型，从而使问题得到解决，有利于提高学生创造性的思维能力。

例：某种病毒具有人传人的特性，若一人携带相关病毒，若未实行有效隔离，经过研究，两轮传染后共有144人患上该种病毒（假设每轮传染的人数基本相同）。问每轮传染中平均每个人对应传染了几个人？

本题考查的是传播问题，可以通过建立一元二次方程的数学模型解决问题。

五、建立不等式模型解决实际问题

在现实问题中，有许多问题很难确定具体的数值，这时教师可以通过问题中的等量和不等量关系列出不等式，可以求出或确定这一问题中某个量的变化范围，从而对所有研究的实际问题有一个比较清楚的认识。这就是不等式模型。不等式建模题型有最佳方案、交通运输、生产规划、方案设计等。

数学建模可以从不同的角度分成很多不同的类型，想要更好地提高学生的数学建模意识，应该从日常生活中学生熟悉的问题入手，帮助归纳不同情况下的不同的模型和方法，让学生在头脑中形成一个数学建模的框架，从而提升学生的数学核心素养。

责任编辑 罗 峰