核心素养视角下初中几何课堂教学的探讨和思考

杨蓓

笔者有一次参加全市初中某个年级的数学期末水平测试的阅卷工作，发现很多学生不会解答一道源于课本的变式题。为什么这么多学生不会解答？我们的几何教学存在哪些问题？如何才能更好地发展学生的几何思维？核心素养视角下初中几何课堂教学应该如何改进？围绕这些问题，我尝试结合这道试题的答题情况对教学进行反思。

一、学生错解中暴露的问题

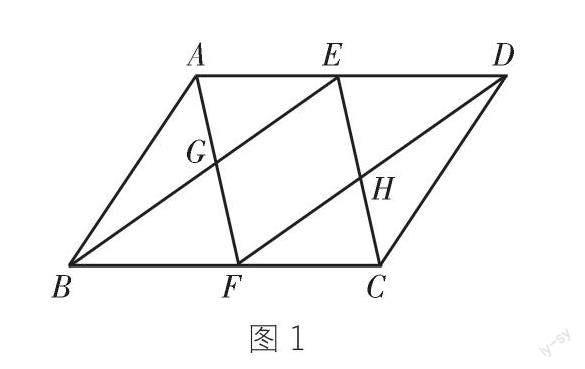
这道试题是這样的：如下页图1，

ABCD中E、F分别是AD、BC中点，AF与BE交于点G，CE和DF交于点H。求证：四边形EGFH是平行四边形。

本题卷面分值7分。这道题是课本例题的变式，而且属于几何证明的基本题型，然而全市学生平均得分仅为3.41分。本题考查的内容是平行四边形的性质与判定，属于平行四边形综合题。我抽查了其中 1600 份试卷，分析这些学生的答案，发现正确解答本题的学生运用了不同的证明方法完成了证明。其中，多数学生由平行四边形的性质得出一组对边平行且相等，再由中点定义得到一组对边平行且相等，从而完成证明；少数学生通过证明三角形全等来完成证明；还有少数学生通过作辅助线来完成证明。同时发现，除了部分学生完全没有作答，相当一部分学生写出的答案基本没有呈现几何证明的思维。学生在答题过程中出现的问题主要表现在：随意添加条件，盲目添加辅助线，过程表达不规范，定理理解不准确，图文不一致，思维定势负迁移等。

二、基于学生错解的反思

为什么学生会出现上述各种各样的错解？除了学生自身的原因之外，教师的教学设计是否存在问题？我们的数学课堂教学应该要注意什么？围绕这些问题，我针对学生的错解作了一些反思。

对于比较抽象的几何知识的学习，如果教师不能采取正确的教学方式，没有结合学生的认知特点进行教学，学生在接受新知识新方法时就会出现很大的困难。这就导致学生在解题的过程中容易因思维定势出现错误，并且相同的错误总会重复出现，因此有必要回到课堂教学环节来查找原因。

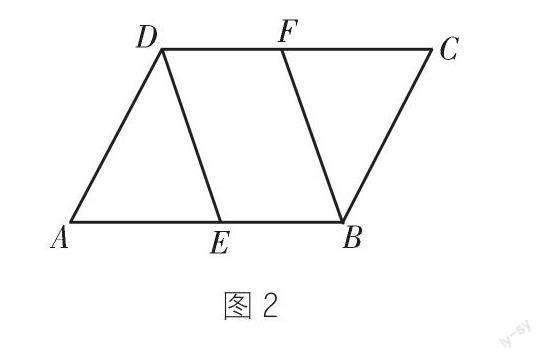
课本里有这样一道例题：如图2，在ABCD中，E、F分别是AB、CD的中点。求证：四边形EBFD是平行四边形。

我对本课时一些课堂实录和教学视频进行整理研究，发现本节课的教学模式一般是“定理—例题—练习—习题”，通过变式训练强调定理的运用。导致学生思维不规范、不完备、不灵活的原因，主要是有些教师忽视了学生的课堂主体地位，没有给学生留出充分的思考时间和空间，也没有回应学生提出的质疑。还比如有些教师在授课时思维不够开阔，回避学生提出的问题，没有让学生经历用全等三角形证明边角相等的过程。事实上，即使学生的方法比较复杂也是他们的一种经历，他们自己会比较和感悟各种方法的优劣。有些教师没有充分发挥典型例题的作用，没有让学生经历概念的发生、发展的过程，缺乏对学生思维能力进行拓展的训练，导致学生形成思维定势。

三、以深度思考促进学生的思维

数学核心素养之一就是会用数学的思维思考现实世界。“图形与几何”的学习与几何直观、推理能力等素养的培养密切相关。

要在几何教学中发展学生的几何直观和推理素养，必须把思考的时间和空间留给学生，让学生经历、体验和享受自主发展数学思维的过程。

要让学生掌握有效的思考方法，优化自己的思维，必须让学生在思考的过程中，在原有认知的基础上拓宽视野，在有关问题上了解更多的知识，养成良好的思考习惯。

教师要引导学生把思维引向纵深，探索正确、有效、简洁的证明方法，将发展学生核心素养落实在课堂教学中，比如对于上述课本例题的教学可以进行如下的改进。

对于上述课本的例题，学生提出用全等三角形来证明时，教师可以引导学生进一步探究，得出下列方案：

教师：用全等三角形如何证明？你能具体说说思路吗？

学生1：由平行四边形的性质得出 ∠A=∠C，AD=BC，又因为AE=CF，可证出ΔAED≌△CFB，从而得到DE=BF，又因为DF=BE，即可证明四边形EBFD是平行四边形。

学生2：我连接 EF，由四边形AEFD是平行四边形，得出DF=AE，又因为AE= BE，可得DF=BE，即可得出四边形EBFD是平行四边形。

此时学生有了从不同的角度来分析问题、运用多种方法来解决问题的经验，教师要通过小结引导学生的思维再往前走一步。“这几种方法中，哪一种最好？为什么？”“平行四边形的证明什么情况下可以利用三角形全等的特点，什么情况下可以利用平行四边形定理？”

这样的设计通过“一题多证”充分暴露学生思维活动的特点，培养了学生思维的求同性，让学生自己灵活选择证明方法，提升学生对课程标准中“四基”的整体掌握程度，从而提高逻辑思维能力。

当学生基本掌握了例题的解决方法后，课堂上可以进一步安排思维跨度较大的题目，让学生对问题进行深度思考。

回到本文开头的试题，在图1的平行四边形ABCD中，E、F分别是AD、BC的中点，连接AF、BE交于点G，连接CE、DF交于点H。

变式问题1：当四边形ABCD是矩形时，四边形EGFH是什么图形？

变式问题2：若将“E、F是AD、BC的中点”改为“AE＝BF”，其他条件不变，画出相应图形，四边形EGFH是平行四边形吗？

总之，核心素养视角下的初中几何课堂教学，需要从传统知识的传授向培养学生的核心素养转变，需要教师落实核心素养目标，体现育人要求，引导学生掌握基本图形的定义、性质与判定方法等，增强学生发现问题、提出问题、分析问题和解决问题的能力，构建由“叶”到“枝”的知识体系，提升学生的思维品质，促进学生形成理性思维和科学精神。

责任编辑 罗 峰