基于基本解法的汽车消声器声学性能分析

张成鑫, 王发杰,b, 吴国正, 程隋福

(青岛大学 a. 机电工程学院; b. 多功能材料与结构力学研究所, 山东 青岛 266071)

对消声器声场进行准确地模拟预测,可为降低排气噪声、功率损失及提高消声器性能提供有力的理论支撑,对汽车消声器分析设计及优化流程等具有非常重要的意义[1]。汽车发动机排气噪声来自发动机活塞四冲程工作循环最后一个阶段[2],即进气、压缩、做功和排气中的排气过程。传统内燃机排气过程由自由排气阶段和强制排气阶段组成[3],排气噪声约占汽车总噪声的55%以上,如何降低汽车排气噪声水平,提高驾驶员和乘客舒适性,已成为各大汽车厂商的研究热点之一[4]。声学系统包括声源、传播途径、接收器[5]3个主要组成部分。目前,降噪处理措施主要从声源及传播途径进行控制[6],从声音源头来控制噪声是最根本有效的措施,但提升相对困难,所以基本都在传播途径中进行合理控制,主要通过消声器来控制排气噪声[7]。声学理论研究和硬件辅助方法逐步完善,各种声学分析也开始使用数值模拟的方法[8]。边界元法[9]在使用中只需要在边界上离散网格单元,降低问题的维数,但是构造的系统矩阵非对称且稠密,使用非常不方便;有限差分法[10]相对比较古老,主要应用领域是流体力学分析;有限元法[11]前处理过程需要在所求区域内划分网格,不仅耗时,而且需要反复修改网格,比较繁琐。基本解法(method of fundamental solutions, MFS)[12]是一种强格式边界型无网格方法,采用基本解作为插值基函数,避免了节点以拓扑的方式连接,可以降低问题的维数。为了防止源点奇异性的出现,该方法在真实边界外引入了虚假边界。陈文等人[13-14]提出一种无需虚拟边界的奇异边界法;L.MARIN等人[15]将此方法用于线性弹性力学反边值问题的数值研究;谷岩等人[16]用MFS分析双材料界面裂纹的断裂力学;A.COLACO[17]用此方法进行分析轨道交通引起的建筑物振动;A.NOORIZADEGAN等人[18]用此方法确定磁场源点的位置。基于此,本文拟采用新型无网格基本解法,对汽车消声器声学性能进行分析。通过借助Matlab平台,采用MFS对二维和三维消声器进行数值模拟。研究结果表明,本方法精度较高,具有一定的可靠性和稳定性。

1 声学问题的基本解法

1.1 Helmholtz方程的声学问题

物体振动发出声音,声音传播需要介质,而介质有一定的质量和弹性,所以会在中间产生压差,由此产生声波。声波在一定范围内传播,传播的范围称为声场[19]。声振是一种物理现象,用传播介质中的声压、质点速度与密度变化量描述声场特性[20]。根据牛顿第二定律、质量守恒定律以及物态方程,得到声压等声学参量随时间与空间的变化关系。声场的这种变化特征可以用数学微分方程来表示,即声学波动方程[21-23],简称声波方程或波动方程。波动方程是一种重要的数学偏微分方程,描述各种波动现象,包括声波、光波和水波等,主要应用于声学、光学、流体力学等领域。波动方程可通过运动方程、连续方程和物态方程推导得到,推导过程如下:

由牛顿第二定律可推导得到运动方程,即在空间中声压的梯度等于质点速度对时间一阶导数和介质密度乘积的负值,其方程为

(1)

其中,∇为矢量微分算符;P为声压;ρ为介质密度;v为质点的振动速度矢量;t为时间。

由质量守恒定律可推导得到连续方程,即介质密度对时间一阶导数等于流体中微小单元质量变化率的负值,描述质点速度和密度之间的关系,其方程为

(2)

物态方程又叫状态方程,描述的是在给定物理条件下的热力学方程,其方程为

(3)

联立式(1)～式(3),消去密度和速度等参数,考虑系统是稳态的,则声压随时间变化规律为简谐运动,有P(x,t)=P(x)eiωt,将此式带入波动方程,即可得到赫姆霍兹(Helmholtz)波动方程为

∇2P+λ2P=0

(4)

其中,λ=ω/c为波数,ω为角频率,c为声速。该方程即声学问题的控制方程,是关于声压的微分方程,描述了稳态声场声压随频率在空间上的分布规律。

1.2 基本解法

考虑二维Helmholtz波动方程,根据MFS数学理论基础,边界点满足边界条件,下面展开介绍此方法的数学理论与数值离散格式求解步骤:

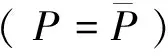
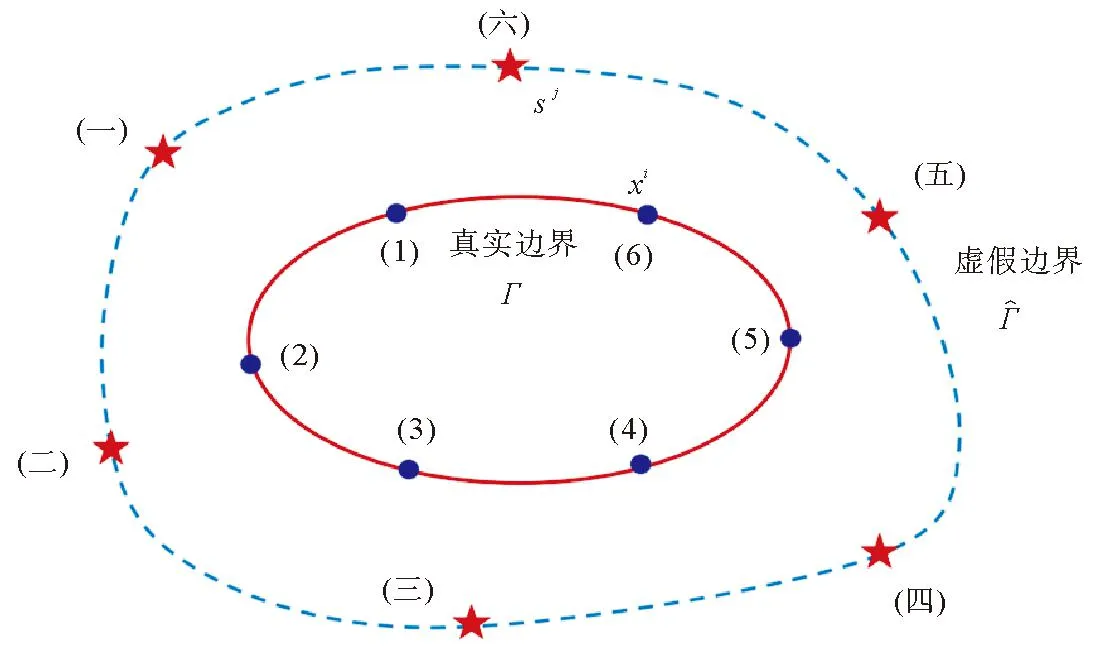
图1 基本解配点

2) 按照数值积分的思想,将每个真实边界点近似表示为离散格式,即

(5)

对满足第一类边界条件的第1个点而言,由已知边界条件可得

(6)

对满足第二类边界条件的第一个点而言,通常此条件为硬边界,由已知边界条件可得

(7)

对满足第三类边界条件的第1个点而言,由已知边界条件可得

(8)

3) 将以上3类边界点的方程组合,可构造得到线性代数方程组,即

(9)

式(9)可简化为

(10)

4) 通过求解式(10),可以得到所有源点密度α,从而可以根据以下表达式求解任意一点处的声压函数值,假设域内待求未知点为x7,所以

(11)

2 方法验证

2.1 二维声学模型

现分析一个经典二维管道声学问题模型,二维管道模型和节点分布示意图如图2所示。管道长为1.0 m,宽为0.5 m,边界为Γ,求解域为Ω,内部介质为空气,气体密度ρ=1.205 kg/m3,声速c=343 m/s。管道左端入口Γ1为声压边界条件,管道内壁Γ2为速度边界条件,右端出口Γ3为阻抗边界条件。该声场解析解为

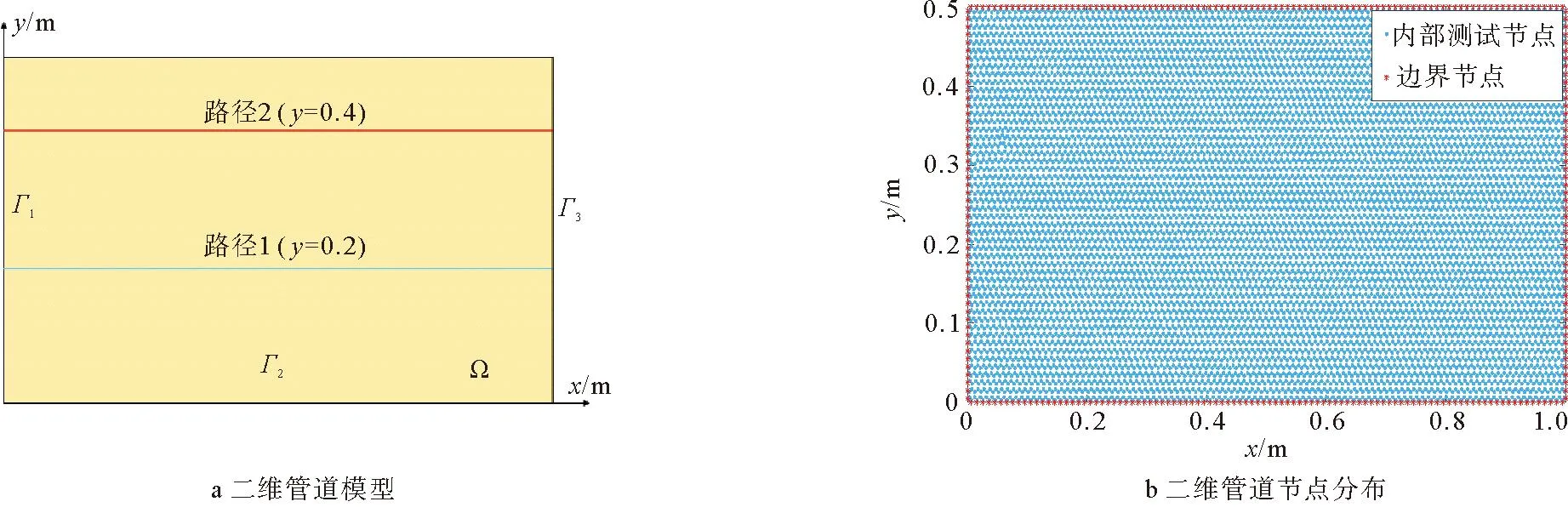
图2 二维管道模型和节点分布示意图

(12)

根据计算需要,首先进行节点离散,节点分布图如图2(b)所示。MFS共离散6 404个节点,其中包括326个边界节点和6 078个内部测试节点,有限元法(finite element method, FEM)中共划分34 954个网格。给定频率为200 Hz,MFS使用Matlab编程求解,二维管道计算域声压分布如图3所示。图3a给出了本方法计算得到的声压值分布结果,图3b和图3c分别为FEM和解析解求得的声场分布图。由图3可以看出,声音沿管道传播,给定的声压沿x轴方向逐步变小降低为0之后反向继续增大,符合声音的简谐运动规律,而且MFS和FEM的计算结果与解析解的声压分布结果非常吻合。以上表明2种方法都有良好的精度,在进一步工作中,FEM结果可作为参考解来检验MFS计算结果的准确性。

图3 二维管道计算域声压分布

为更好地验证MFS的计算精度,将声压值同样进行数字化,给定2条路径,如图2a所示,分别为路径1(y=0.2)和路径2(y=0.4)。在2条路径上等步长均匀选取20个点作为测试点,给出MFS、FEM和解析解在测试点处的声压值曲线,不同测试点路径上节点的声压分布如图4所示。由图4可以看出,两者计算结果和解析解结果几乎重合,无网格方法准确性得到了保证,为汽车发动机排气消声器声学研究提出一个新的解决方案。

图4 不同测试点路径上节点的声压分布

2.2 三维声学模型

将验证思路拓展到三维,三维管道模型示意图如图5所示。图5中,考虑三维圆柱形管道计算域Ω,长0.3 m,内直径0.12 m,内部为空气介质,其密度ρ=1.205 kg/m3,声速c=343 m/s。在左侧入口Γ1均匀施加声压边界条件,内壁Γ2为刚性壁面声学硬边界,出口Γ3为阻抗边界,用此简单模型验证MFS的计算精度。

给出此声场的解析解为

(13)

借助Matlab计算和Comsol有限元软件进行仿真分析,给出了频率f=500 Hz时的三维管道模型表面声压分布情况,三维管道表面声压分布如图6所示。图6a和6b分别为MFS和FEM的计算结果,图6c为解析解给出的表面声压分布。由图6可以看出,MFS和FEM与解析解非常一致,保证了计算准确性。

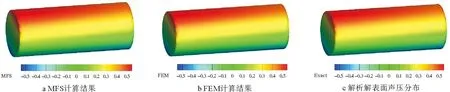
图6 三维管道表面声压分布

给出频率f=300 Hz时,内部测试节点处MFS计算得到的声压值绝对误差曲线,计算域内节点声压绝对误差分布如图7所示。由图7可以看出,本方法计算值和解析解结果误差非常小。综合考虑以上情况,MFS可继续分析计算模拟其他复杂三维几何模型的声场分布情况。

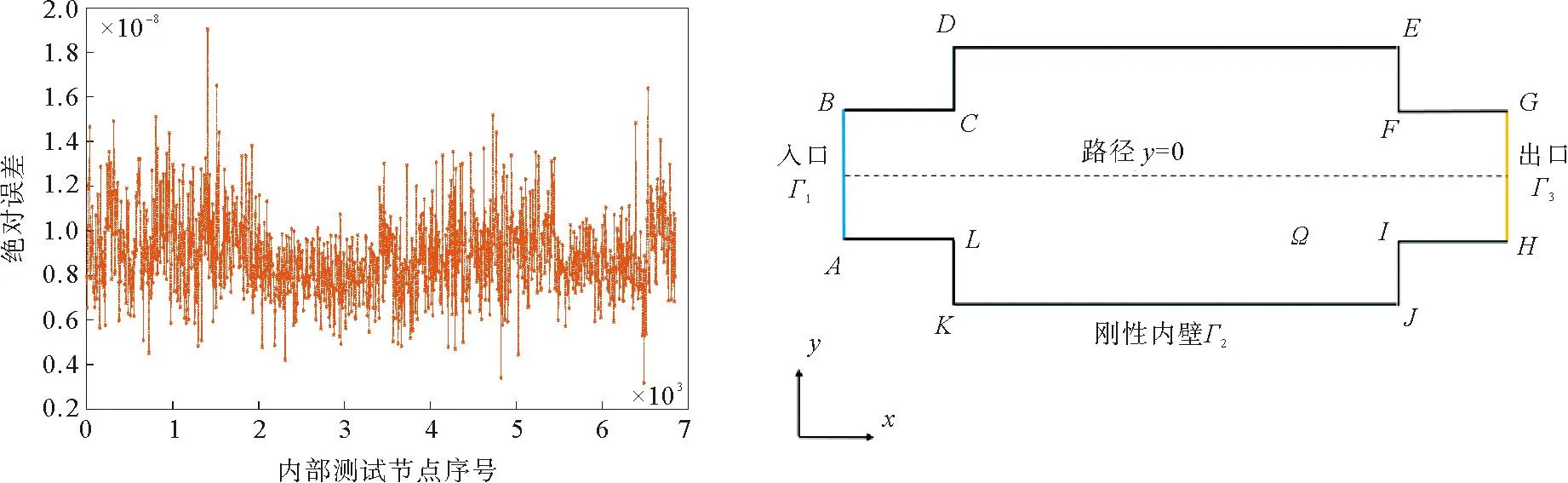
图7 计算域内节点声压绝对误差分布

3 算例

3.1 二维算例

考虑一个二维扩张室消声器平板模型计算区域Ω,总长度为0.3 m,宽度为0.12 m,进出口长度等长,BC=FG=0.05 m,宽度等宽,AB=GH=0.06 m,其他参数均在理想条件下为固定值,包括内部气体密度ρ=1.205 kg/m3,声速c=343 m/s。控制方程为Helmholtz方程,在消声器左端入口Γ1处,施加第1类边界条件,单位声压P=1.0 Pa,右端出口Γ3为阻抗边界条件,阻抗值ZS=413 Pa·s/m3,其他为刚性边界Γ2。用FEM计算得到的数据作为参考解来验证此方法的精确性。二维消声器几何模型示意图如图8所示。

给定频率为f=500 Hz时,计算MFS和FEM在求解域内的声压值,二维消声器计算域声压分布如图9所示。由图9可以看出,声音在内部以平面波的形式沿管道轴向传递,消声器入口处的声压数值最大,且沿x轴正方向呈下降趋势。MFS和FEM计算结果显示,两者吻合度较高,MFS在求解二维消声器声学问题中结果表现良好,为后续研究三维消声器声学问题作了铺垫。

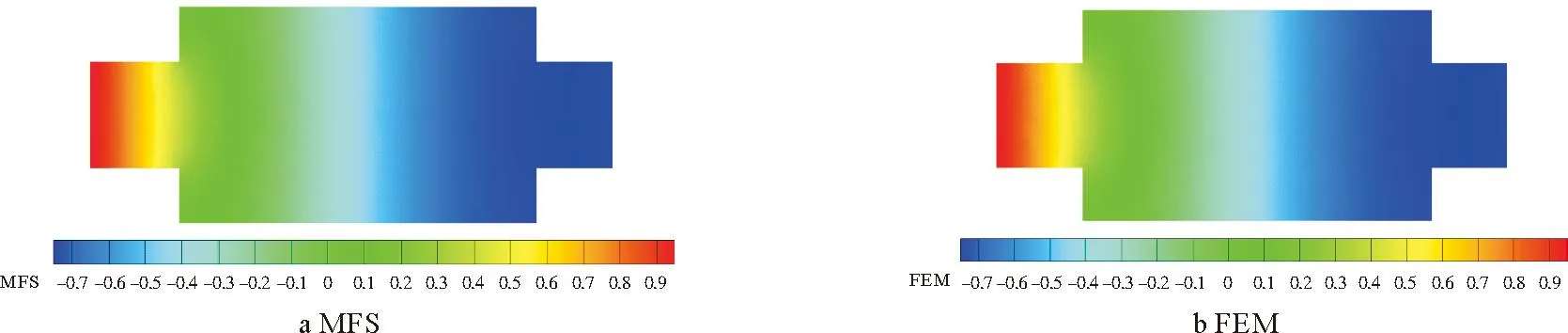
图9 二维消声器计算域声压分布

在消声器中轴线y=0上,均匀选取30个测试点,计算域内路径y= 0上节点声压与误差值曲线如图10所示。图中在频率f=500 Hz时,MFS和FEM计算得到的声压曲线与在此状态下2种方法之间的绝对误差曲线。由图10可以看出,MFS计算得到的结果均分布在FEM曲线附近,MFS表现出良好的计算性能,最大绝对误差仅为2.1074×10-4,表明MFS构造虚拟源点并且使用基本解插值基函数时,解决了源点奇异性问题,同时也保证了计算精度,提高了计算效率,具有良好的平顺性与光滑性。

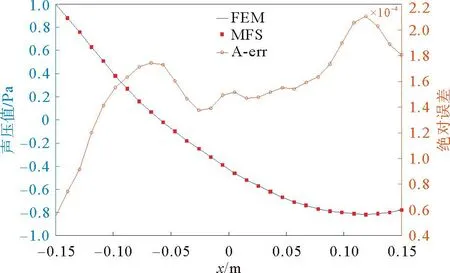
图10 计算域内路径y= 0上节点声压与误差值曲线

对于大多数内燃机汽车的消声器,由于其进出口的管径相对内部腔体的管径较小,声波截止频率较高,因此在工程问题中,考虑的频率范围内的声波可认为以平面波形式传播,所以计算传递损失时,进出口声压可取截面中某一点代替整个截面的声压[26]。汽车噪声频率通常在100～2 000 Hz范围内,所以传递损失在此频率范围内进行分析。在100～2 000 Hz频率范围内,二维消声器的传递损失曲线如图11所示。由图11可以看出,MFS和FEM计算得到的传递损失几乎重合,说明计算过程准确。随着频率升高,传递损失整体呈上升趋势,在800 Hz和1 400 Hz时,传递损失出现峰值,表明在此频段消声器消声效果最显著。而在100～500 Hz频率消声效果不理想,是因为此结构模型和真实消声器结构上存在一定差异,在低频情况下没有达到理想的消声效果。

消声器结构参数对改变消声器消声性能起着关键作用,其中进出口宽度对其性能有重要影响,不同进出口宽度下的传递损失曲线如图12所示,图中为进出口宽度分别为40 mm和80 mm时的传递损失。由图12可以看出,在2种不同进出口宽度的情况下,传递损失呈现周期性增加的趋势。进出口宽度为40 mm消声器的传递损失略高于80 mm消声器,原因是进出口管径过大,声音进入消声器膨胀腔内干涉较少,扩张室作用不明显,大多声音可以顺利传出,导致消声效果不明显。

3.2 三维算例

将MFS应用拓展到三维具有外插进出口管的膨胀腔消声器的声场问题中,三维消声器局部剖面图如图13所示。求解域为Ω,外形尺寸和上节一致,横向总长0.3 m,内部扩张室直径为0.12 m,进出口等长为0.05 m,直径为0.06 m,内插管长度为0.05 m,厚度均为0.002 m,内部气体密度ρ=1.205 kg/m3,声速c=343 m/s。考虑到发动机排气产生的噪声为消声器内部声音的重要来源,综合汽车发动机运行工况,因此假设在左侧入口Γ1处给予单位声压,出口Γ3处为带阻抗的边界,阻抗值Zs=413 Pa·s/m3,其余Γ2均为声学中的硬边界。

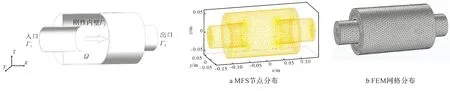
图13 三维消声器局部剖面图

为分析提出的无网格MFS在计算消声器三维声场分布问题的准确性,首先进行节点离散。三维消声器计算域单元离散示意图如图14所示,共有20 714个节点,包括13 350个边界节点和7 364个内部测试节点,MFS节点分布如图14(a)所示,FEM中共划分94 667个网格,FEM网格分布如图14(b)所示。由于本问题没有精确解进行对照参考,所以同样将有限元仿真模拟软件COMSOL得到的结果数据作为参考解进行比较分析。

综合汽车运行工况和消声器的特点,选取频率为500 Hz进行研究分析。三维消声器计算域表面声压级分布如图15所示。由图15可以看出,MFS和FEM计算得到的表面声压级数值非常接近,声音进入消声器扩张室之后,在其内部反射、碰撞并互相干涉,声压级逐渐下降。综合图像显示,一方面表明消声器消声特点以外,另一方面也表明MFS计算具有良好的准确性。

图15 三维消声器计算域表面声压级分布

消声器作为一种用于汽车排气消声的零部件,出口声压值非常重要,所以在出口截面取若干个点作为测试点,准确展示本方法的计算结果,测试与FEM之间的绝对误差。三维消声器出口测试点声压值曲线如图16所示。由图16可以看出,两者计算结果均在同一数值附近,也验证了在消声器内部,声音的确以平面波形式进行传播。给出本方法和FEM之间的绝对误差,三维消声器出口测试点声压绝对误差值曲线如图17所示。由图17可以看出,误差控制在3.325×10-3以内,精度得到保证,为进一步分析消声器的传递损失奠定良好的基础。

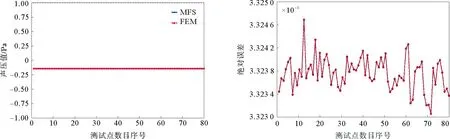
图16 三维消声器出口测试点声压值曲线

消声器消声原理为声波在其内部碰撞、干涉等,使声音减弱,所以其设计结构对消声性能有重要影响。由本章第三节分析显示,汽车正常运行工况下,根据汽车发动机转速和气缸数可得,排气噪声频率控制在100～2 000 Hz,所以本次传递损失同样仅考虑在此范围内的计算结果。三维消声器的传递损失曲线如图18所示。由图18可以看出,两种方法吻合度良好,频率均在700 Hz与1 400 Hz时达到峰值,说明在此频段消声效果最佳,其传递损失数值分别为43.265 1 dB和42.846 2 dB。而在1 700 Hz频段附近传递损失非常小,有大幅度下降,根据研究表明,这是由径向声学模激励引起。综合曲线显示,本方法在计算三维消声器模型的传递损失时准确性与求解精度较高。

图18 三维消声器的传递损失曲线

带有进出口内插管的消声器,内插管的长度对消声器性能有非常重要的影响。给出了内插管长度分别为20,50,80 mm 3种情况,分别计算传递损失并绘制曲线,不同内插管长度的传递损失曲线如图19所示。

由图19可以看出,在700 Hz和1 400 Hz频率下,三者传递损失最突出,说明在此消声频段消声器消声能力最强。随着频率地增加,三者趋势整体一致,内插管长度为50 mm时消声器效果最好,插管长度为20 mm时消声器效果最不理想。在内插管长度到达一定值时,传递损失曲线存在一个驻点,在驻点之前,随着内插管变长,传递损失越来越大,消声效果越来越好;而驻点之后,随着内插管长度增加,消声效果会有所减弱。所以合理选择内插管长度对提高消声器消声性能尤为重要。

4 结束语

本文使用数值模拟方法对消声器进行声学预测,即采用声学的Helmholtz波动方程进行数值计算分析,借助无网格方法对汽车排气消声器声学问题进行计算求解。系统分析了算法的优化参数以及消声器的结构参数对结果精度和稳定性的影响,通过消声器声学模拟验证了算法的可行性,研究表明,该无网格数值方法精度较高,简单易操作且保证了计算效率,声场分布光滑且一致性好,表明此方法有一定的有效性以及稳定性,为声学问题提供了一种便捷、准确、可靠的计算工具。下一步可从消声器声-固耦合问题以及消声器几何设计优化设计等方面进行深入分析。