资源密集型NTT 算法硬件设计与实现研究*

王明东，梅 瑞，吴朋庭，李 军，何卫国，毛发英

（成都三零嘉微电子有限公司，四川 成都 610041）

0 引言

美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）自2016 年12 月开始面向全球公开征集并制定后量子密码算法，在所有候选算法中，基于格理论的后量子密码算法在数量上占据明显优势。同时整数型、浮点型主流全同态密码算法，如BGV[1]、BFV[2]、CKKS[3]算法均是基于格理论的密码体制。格基密码方案的计算主要是基于多项式环开展，涉及多项式环上的加/减法、乘法、模约减等运算，其中加/减法的计算复杂度为O(n)，朴素乘法的计算复杂度为O(n2)。随着多项式阶n的不断增大，多项式乘法运算变得异常复杂。相较于CRYSTALS-KYBER 等后量子密码算法中环上多项式阶与模数较小，在硬件设计时不存在资源利用的瓶颈[4]，而在全同态密码算法中，多项式的次数可以达到上万阶，模数达几百比特，是一种资源密集型算法，在硬件实现整个架构中，多项式乘法部分是最耗时、最耗资源的模块。

目前快速数论变换（Number Theoretic Transforms，NTT）是多项式乘法中最有效的方法之一。NTT算法的本质是定义在有限域上的快速傅里叶变换（Fast Fourier Transform，FFT），使用有限域上的单位原根代替了FFT中的复数原根，由模上的整数运算代替了浮点数运算。使用快速NTT 算法能够将多项式环上乘法的计算复杂度由O(n2)降为O(nlog2n)，当多项式的阶数n增大时，NTT 算法优势明显。高效率的NTT 算法实现是后量子与同态密码算法最关键的核心。

本文基于全同态密码算法资源密集型的特点，结合典型NTT 算法实现流程，分析NTT 算法硬件实现的关键问题与难点，提出多周期并行化设计与全流水化设计两种硬件方案，并对方案的资源消耗与性能进行对比分析。在资源与性能折中的情况下，采用流水化设计具有较高的资源性能比，为优先方案；若完全以性能为主，在资源尽可能满足的条件下，可采用多周期并行化方案，同时进一步提高蝶形运算并行度，获得更高的性能需求。

1 NTT 算法简介

快速数论变换NTT 算法可以看作离散傅里叶变换（Discrete Fourier Transform，DFT）在有限域上的推广形式，其运算流程与快速傅里叶变换的思想相同，主要是通过对多项式在特殊点进行求值运算将多项式的系数表示转变为点值表示，并将求值点选择在n个单位原根（FFT 为n个单位复根）处，则可以通过迭代运算的方式完成点值运算，其时间复杂度为O(nlog2n)。

Zq表示整数环模q的商环，Rq=Zq[x]/φ(x)表示模多项式φ(x)的整系数多项式环，其中φ(x)为不可约简多项式。对于同态密码算法，大部分情况下φ(x)=xn+1。Zq的n次单位原根ωn满足ωnn≡1 modq，且当0＜i＜n时，对于多项式a(x)∈Rq，其系数为(a0,a1,…,an-1)，对a(x)在旋转因子ωni处进行求值，可以得到其点值表示，其中满足∀i∈[0,n-1]。

式中：⊙为卷积。

对于同态密码算法中的多项式环Rq=Zq[x]/(xn+1)，ω，ϕ分别表示n阶、2n阶的原根，那么xn+1 可以分解为

因此，可以得到NTT 运算对应的矩阵形式为：

可以看到，Rq=Zq[x]/(xn+1)上的NTT 运算实际上是先对a(x)∈Rq做预处理变换a'=(a0,a1,…,an-1)⊙(ϕ0,ϕ1,…,ϕn-1)，然后进行标准的NTT 运算。相应地，环上多项式乘法表示为：

NTT 典型算法流程如下：

2 关键问题分析

2.1 存储开销大

在环上容错学习问题（Ring Learning with Errors Problem，RLWE）的全同态加密方案中，为了获得更深电路的计算，希望模数q取得尽可能的大，同时为了保证方案的安全性，在q增大的同时，可以增加环多项式维数N的值，所以q与N在全同态加密方案中需要一种平衡，以保证方案的安全性和同态计算能力。

对于k比特安全性，满足如下关系式[6]：

以128 bit 安全，典型安全参数为q=256 bit，维数N为8 192，单个参数可达256 KB。当安全强度增大时，参数的存储量呈爆炸式增长。

因此，在存储的使用上，尽量采用单口（Single Port）SRAM，避免使用双口（Dual Port）SRAM 进行设计。

2.2 存储跨越式访问

NTT 算法本质上是以蝶形单元为基本操作，共log2n层，每层的蝶形单元为n/2 个，共(n/2)×log2n个蝶形操作。以维数n=8 进行分析说明，如图1 所示。

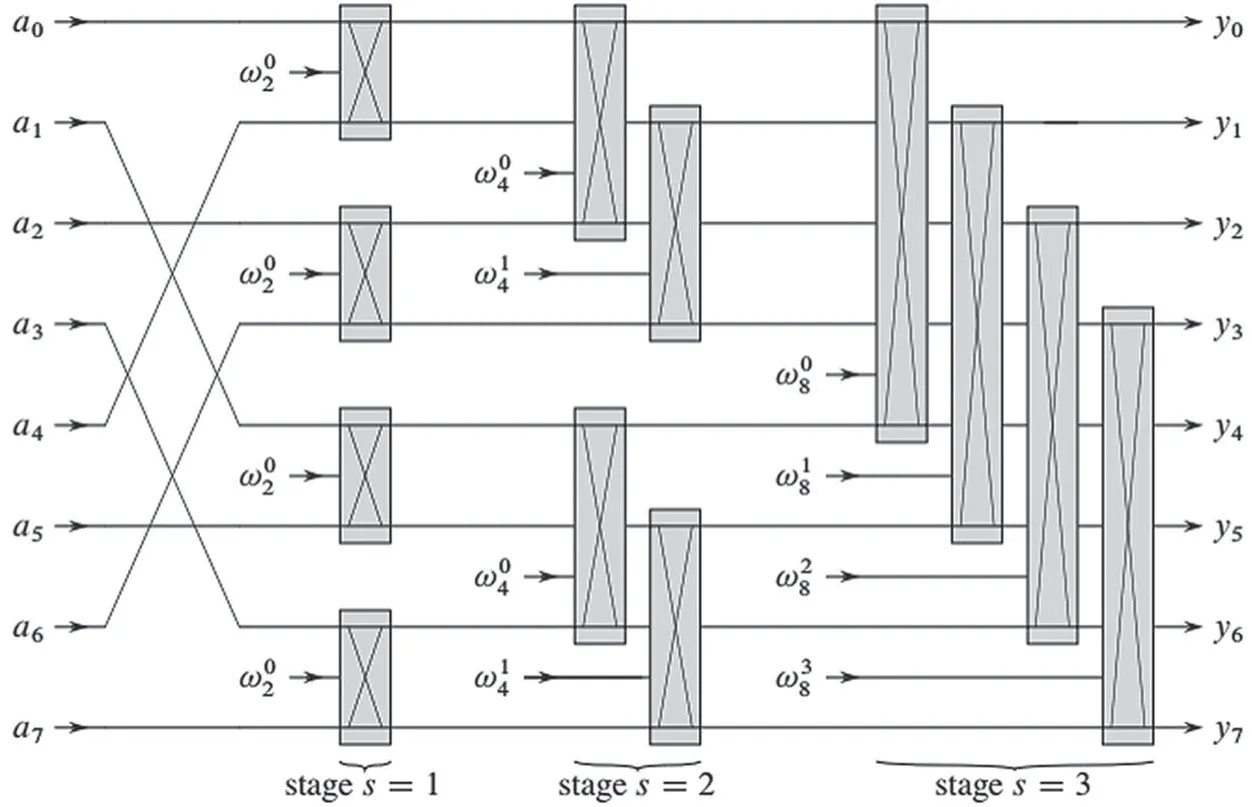
图1 蝶形单元存储跨越式访问

第1 层存储访问：（0,4），（1,5），（2,6），（3,7）。

第2 层存储访问：（0,2），（1,3），（4,6），（5,7）。

第3 层存储访问：（0,1），（2,3），（4,5），（6,7）。

可以看到，存储跨越式访问为算法的高并行或者流水线设计带来了特别大的设计困难。

2.3 读写冲突问题

NTT 算法的蝶形单元操作为算法1 中描述的7～11 步操作。蝶形单元结构如图2 所示。

图2 蝶形单元结构

为了减少存储资源的开销，在设计上应尽量避免使用双口SRAM。因此，上述蝶形单元中对存储的两次读、两次写操作，以及存储地址的跨越式访问，不论采用并行化设计还是流水线设计，都将不可避免地带来存储的读写冲突问题。

2.4 减少额外的存储访问

由于同态密码算法多项式环的维数n通常可达210～217，额外的存储访问开销将直接带来NTT 算法性能的明显降低。

（1）避免对数据的直接Bit Reverse 操作：算法1 流程中的Bit_Reverse_Copy(a’,A)应当直接避免。

（2）NTT运算后的结果，应可直接作用于INTT 运算，避免增加额外Bit Reverse 操作。

2.5 算法设计问题

NTT 算法的标准流程为3 层的for 循环描述，不利于硬件化的高效实现。因此，需要对算法的第2、第3 次循环进行展开式描述，以方便实现高并行或者流水化设计。但是，这会进一步增大存储的跨越式访问与读写冲突问题。

3 硬件设计方案

3.1 NTT 算法流程优化

3.1.1 规避Bit_Reverse_Copy 操作

规避算法1 流程中的Bit_Reverse_Copy(a’,A)操作，即数据的比特逆序拷贝操作。蝶形运算单元中，对存储地址直接进行比特逆序访问。

3.1.2 蝶形单元并行化展开

NTT 的算法描述为3 层for 循环，不利于按层次化进行蝶形单元运算流程控制和并行化设计。因此将后两层for 循环描述进行合并，提出以下并行化地址映射算法流程以2 路并行为例，算法相应地可扩展为多路并行运算，地址映射如下所示。

3.1.3 INTT 优化

INTT 在NTT 的算法流程下，最后一步对所有多项式环系数参数需要做模逆n的操作，由于n是2 的幂次，因此可等效在每层的蝶形操作上增加模除以2 运算，省略INTT 最后的模逆n运算，提升性能。其中，模除以2 运算可优化设计为：

通过向右移位、加法和逻辑与进行实现，简化x除以2 的求模运算。

3.1.4 NTT/INTT 复用

对NTT 的运算进行正向位序数据输入，比特逆序位序输出。对INTT 的运算采用比特逆序位序输入，正向位序数据输出。

采用上述处理方式，复用NTT/INTT 模块，减少硬件资源使用，无须再对数据进行比特逆序操作，只用改变相应的旋转因子，以及INTT 的蝶形单元操作多一个模除以2 运算。

3.2 模乘算法方案

蝶形单元操作中涉及一次大整数的模乘运算。为支持大位宽的模乘运算，同时使模数q具有灵活性，采用经典的Montgomery 算法。算法描述如下：

算法3 中，步骤1 到步骤3 为3 次乘法，分别占用1 个周期，步骤4 到步骤6 一共占用1 个周期，那么一次完整的模乘运算需要4 个周期来完成。

3.3 多周期并行化方案

结合模乘算法方案，将模乘运算的最后一步减法与蝶形操作的一次模加、一次模减进行合并，蝶形单元的单次操作可细化为图3 的形式。

图3 蝶形单元单次操作

（1）若采用单口SRAM 进行数据存储，共需8 个周期完成一次蝶形操作。

（2）若采用双口Dual Port SRAM进行数据存储，将两次读和两次写操作同批完成，共需6 个周期完成一次蝶形操作。例如，在性能提升25%的情况下，以单双口面积的初步比例估计，存储将翻倍增长。同时，若需要达到(n/2)×log2n的性能规模，需要同时并行8 个或者6 个蝶形单元，并将SRAM 分成8 个或者6 个BANK 并行访问，随之带来的是乘法器与加法器的成倍数增长。

（3）多周期并行化处理需要解决算法层地址比特逆序访问的并行化处理，为并行化处理的关键核心。可采用算法2 中的蝶形单元并行化展开的算法流程。

3.4 流水化方案

3.4.1 流水线划分

NTT 算法的本质是(n/2)×log2n个蝶形运算操作，考虑全流水化方式设计。

原始蝶形单元操作如图4 所示。

图4 原始蝶形单元操作

为方便流水线设计，将两次读与两次写分别合并，设计6 级流水线，如图5 所示。

图5 蝶形单元6 级流水

图5 中，DR 为单周期两次读操作，M1 为第一级乘法，M2 为第二级乘法，M3 为第三级乘法，A为模乘的最后一级减法、蝶形操作的模加、模减、INTT 的模除以2 操作的集合，DW 为单周期两次写操作。

3.4.2 存储设计

由于同态密码算法的NTT 运算存储资源消耗巨大，在存储的使用上采取以下策略。

（1）为节省面积，首选单口SRAM 缓存数据。

（2）为解决DR、DW 的流水读写访问冲突，采用乒乓BUFFER 的思路，如图6 所示，将每层的结果写入另一块RAM。同时，多项式乘法时，可复用此RAM。

图6 乒乓RAM

（3）将单个数据存储划分为2 个BANK，支持单周期两读两写操作，同时方便蝶形操作。

（4）对于NTT 与INTT 的旋转因子，可选择同步计算匹配或静态预先存储。若考虑静态型，旋转因子数据可存储在ROM 中。

3.4.3 蝶形地址映射

全流水设计的蝶形地址访问是NTT 算法设计最关键的要素。以n=16 进行说明，地址实际访问序列如图7 所示。

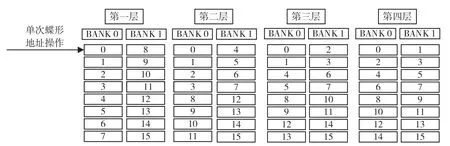
图7 蝶形单元地址访问序列

（1）首先，将0～7 位序数据存储在BANK0 的0～7 地址；其次，将8～15 位序数据存储在BANK1的0～7 地址。形成第一层的蝶形比特逆序访问。

（2）完成单次蝶形运算后，按正常流程，如（0,8）序列对，运算结果需要相应地写入实际地址0、地址8。但是，第二层的0、8 地址位于同一个BANK，将造成单周期两次读的冲突，并且不满足第二层（0,4）蝶形序列对的要求。相应地，提出以下的存储调整方案思路，如图8 所示。

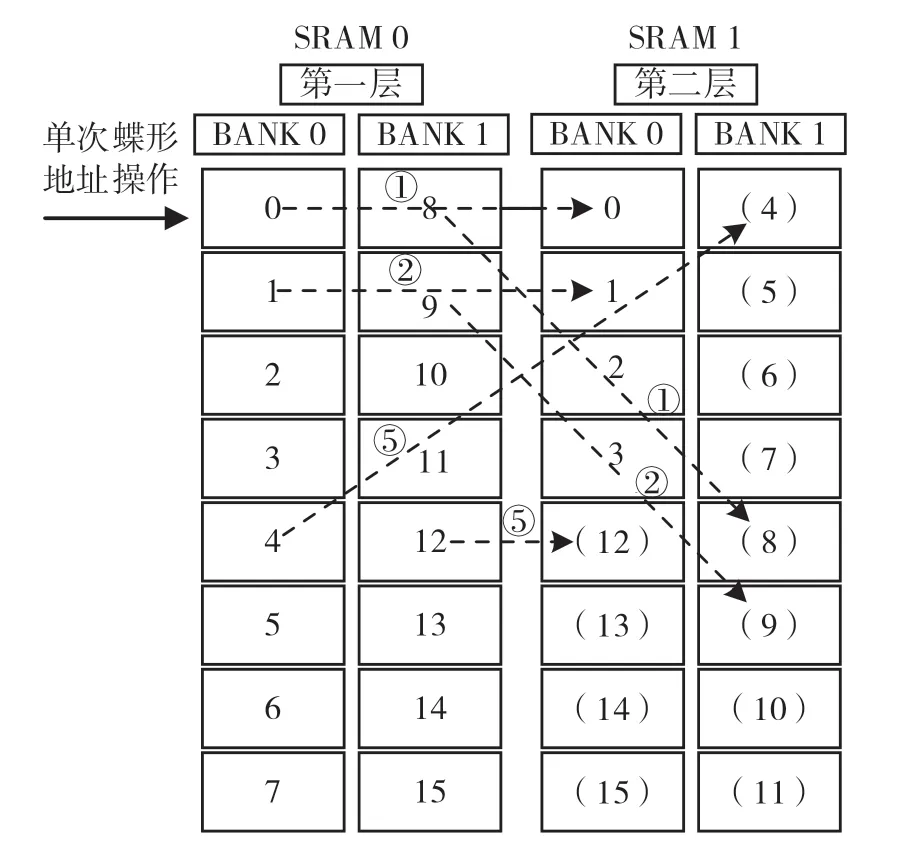
图8 蝶形单元地址调整方案

①将SRAM0 蝶形操作（0,8）位序的0 位序结果写入SRAM1 BANK0 的0 位序，8 位序结果写入SRAM1 BANK1 的4 位序。

②将SRAM0 蝶形操作（1,9）位序的0 位序结果写入SRAM1 BANK0 的1 位序，9 位序结果写入SRAM1 BANK1 的9 位序。

③以此类推，形成图8中第二层的存储分布关系。

（3）调整读顺序，匹配实际读序列对的需求。

调整后的位序同实际的位序位置关系对比如图9所示。

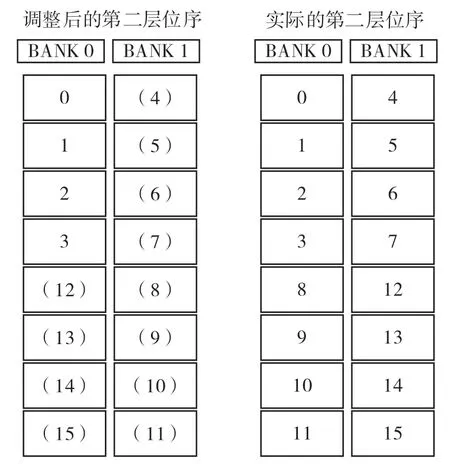
图9 蝶形调整地址与实际地址对比

可以看到，只需要对带双括号的读顺序进行互换，就可满足真实的蝶形比特逆序操作，问题得以解决。

3.4.4 旋转因子

旋转因子模块是NTT 中的重要子模块，在实现中分为动态运算型旋转因子电路与静态存储型旋转因子电路。

动态型的资源花费主要在模乘运算上，在流水化设计中，需要提前启动旋转因子的运算，与NTT运算流水线进行匹配，如图10 所示。同时需要调整蝶形的地址映射，使旋转因子的模幂指数连续化。以n=16 为例，动态运算型需存储对应每层的单位根，共log2n=4 个数据，第一层ϕ0，第二层ϕ8，第三层ϕ4，第四层ϕ2，ϕ为2n阶原根。每层经模乘器运算动态匹配，旋转因子存储量由n/2 减少到logn。

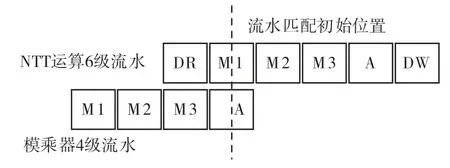
图10 旋转因子动态计算流水匹配

静态存储型旋转因子电路由RAM 或者ROM 存储所有运算的旋转因子和相关参数。与动态型相比，静态型只花费存储资源，且主要与数据宽度和多项式维度n相关。旋转因子的数据深度为n/2。

3.4.5 流水中断

考虑以下两个问题。

（1）如果采用动态型同步计算旋转因子的方式，须将旋转因子的地址映射调整为连续性访问（旋转因子为连续型模乘运算），对应的蝶形单元的地址映射为比特逆序操作。由于是地址比特逆序的访问操作，在每层流水分界线前后，将带来读写数据相关性问题。

（2）如图11 所示，在NTT 运算每层的流水分界线后，同一时刻的下一层DR 与上一层的DW 操作将产生同片RAM 读写冲突问题。

图11 流水读写冲突

在上述两个问题中，问题（1）的处理方式一般采用数据前推操作，但是比特逆序的前后相关性问题在相关性的直接判断上，难以进行统一判断处理。结合问题（2），直接采用中断流水的方式，可同时解决问题（1）和（2），如图12 所示。

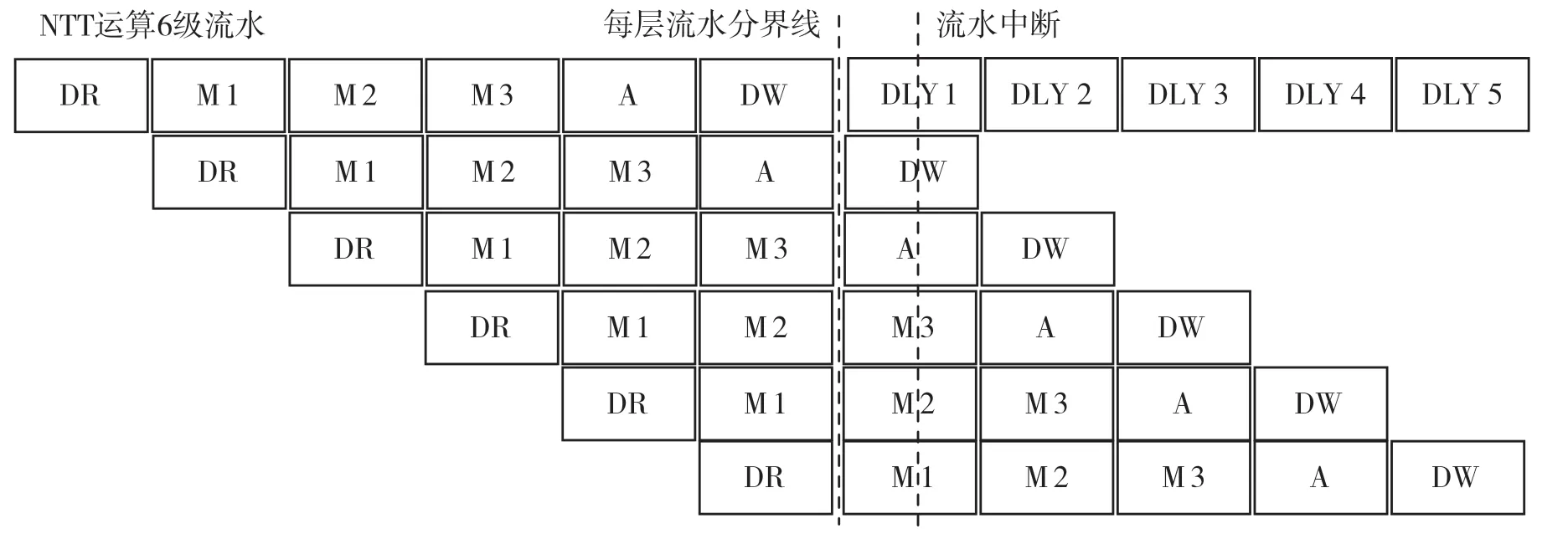
图12 流水中断

在性能上，由于每层蝶形运算将中断5 个周期，性能降低约5/(n/2)，n通常取8 192，163 84 等，降低约0.1%及以下，可忽略不计。

3.4.6 模块整体结构

NTT 算法流水化设计整体结构如图13 所示，包括流水化蝶形单元、存储模块、地址映射模块等。

图13 NTT 算法流水化设计整体结构

ntt_pipe：6 级流水的访问控制、存储的读写访问控制。

butterfly_pipe：蝶形单元的4 级流水运算。可同时支持6 级流水蝶形运算，4 级流水模乘操作，单周期的模加、模减运算。

madd_alg：模乘运算的最后一步减法操作、蝶形模加、蝶形模减、模除以2 运算。

addr_reflect：地址重映射，每层运算实际位序的调整。

bit_rev：地址逆序模块，对最后一层蝶形运算的数据调整，用以支持INTT 运算的位序以及结果的正常序输出。

SPRAM0/1：数据存储器，存储多项式系数。

ROM：mtwd 模块存储NTT 旋转因子；minvtwd模块存储INTT 旋转因子。

3.4.7 性能评估

采用单蝶形单元全流水实现，NTT/INTT 运算的周期数约等于(n/2)×log2n个周期。当n=256 时，约1 000 个周期；当n=8 192 时，约5.3 万个周期。

当n=256 时，硬件RTL 代码仿真波形如图14所示，一次NTT 运算的周期数为1 065，同时经INTT 运算后，数据可成功还原。

图14 NTT 算法流水化实现仿真验证波形

3.5 方案评估对比

以(n/2)×log2n个时钟周期为等同参考量：若n=8 192，q=256 bit，时钟频率约束500 MHz 的情况下，一次NTT/INTT 约耗时0.1 ms。方案评估结果对比说明如表1 所示

表1 方案评估结果对比说明

在资源的消耗上，若采用静态型旋转因子，单蝶形单元流水化设计需要3 个乘法器以及一组乒乓SRAM（即两个单口SRAM）。

多周期并行化方案，若采用双口SRAM，蝶形单元需要1 个乘法器，单次蝶形操作需要6 个时钟周期，因此在并行6路的情况下，共使用6个乘法器。若采用单口SRAM，则单次蝶形操作需要8 个时钟周期，并行8 路共使用8 个乘法器。

若采用动态型旋转因子，乘法器资源相对于静态型旋转因子方案将翻倍。

因此，在资源与性能折中的情况下，采用流水化设计具有较高的资源性能比，为优先方案；若完全以性能为主，在资源尽可能满足的条件下，可采用多周期并行化方案，同时进一步提高蝶形运算并行度，获得更高的性能需求。

4 结语

本文针对典型整数型、浮点型全同态密码算法资源密集型的特点，结合典型NTT 算法的实现流程，分析了NTT 算法硬件实现的关键问题与难点，为了支持算法参数的普适性，基于Montgomery 模乘算法结构，提出了多周期并行化设计与全流水化设计方案。方案中重点给出了蝶形单元并行化展开的地址映射算法，分析了全流水化设计的核心要点并给出了模块整体结构以及仿真验证结果。最后对两种实现方案进行了资源性能的对比分析，依据资源和性能需求，为资源密集型NTT 算法的高效硬件设计提供参考。

另外，为了进一步提高整个模块或系统的频率，针对同态密码算法的大位宽乘法器，可采用Wallace 压缩树[8]，对乘法器进行两级或多级展开。在性能资源等同参考量下，对于多周期并行方案，将直接增加并行度的资源消耗，相应地，流水化设计仅增加流水深度和少量流水寄存器消耗，因此流水化设计将更具优势。