水泥原料辊压产品粒度特性方程式的研究
2023-12-30潘卫宁杨纪昌王亚珍仝丽娟
潘卫宁,杨纪昌,王亚珍,仝丽娟
1洛阳矿山机械工程设计研究院有限责任公司 河南洛阳 471039
2智能矿山重型装备全国重点实验室 河南洛阳 471039
物料粒度分布的表示方法有表格法、图示法以及粒度分布方程法,粒度分布方程是根据物料的粒度筛分数据,运用数学分析方法建立的。物料的粒度分析,通常是由一系列尺寸的筛网筛分获得的,其结果是一组离散的点,粒度方程可以对复杂的筛分数据进行概括、描述,可以便捷地计算各粒级的产率,避免了繁杂费时的筛分工作,尤其是对较难进行筛分的小粒级。侯英等人对粒度特性参数与粒度分布均匀程度的关系进行了研究,利用粒度方程式进行物料颗粒的比表面积计算及均匀性分析,以反映物料的均匀程度[1]。近年来,也有学者将粒度特性方程式与碎矿、磨矿的功耗相联系,成为研究碎磨过程的重要手段[2]。
多年来,学者已经通过统计方法总结出 10 余种粒度方程,应用较广的粒度方程有高登 Gaudin 方程(简称 G 方程) 和罗任-拉姆勒 Rosin-Rammer (简称 RR方程)。实践证明,G 方程对粗、中碎产品或对辊压机、棒磨机产品较为符合,RR 方程则对破碎的煤、细碎的矿石和细磨的矿料以及水泥等较为符合[2]。段希祥教授对球磨机产品粒度特性进行研究,分析了 G方程和 RR 方程之间的关系[3];邬小骐等人对破碎产品的粒度特性方程进行研究,建立了常用破碎设备的排矿标准粒度曲线[4];刘晨敏等人对原生煤粉粒度特性进行研究,证实了原生煤粉粒度特性符合 RR 方程[5]。辊压机 20 世纪 80 年代被引入国内,广泛应用于建材、矿山等行业,在生料和水泥粉磨系统节能优势较为明显[6-7]。丁凯等人的试验研究,证实了辊压机在铁矿石粉磨中的节能效果[8];中信重工杨纪昌等人经过多年努力,建立了用于矿山和建材领域的辊压机选型试验方法[9]。目前对于辊压产品粒度特性方程的研究鲜见有报道。辊压机的破碎机理与传统破碎机、球磨机显著不同,其破碎产品的粒度分布理应与传统的碎磨设备有所不同。笔者借助近年在实验室进行的水泥原料辊压产品粒度筛分数据,对 G 方程和 RR 方程进行验证、分析,探讨适合水泥原料辊压产品粒度分布描述的粒度方程。
1 常用粒度方程介绍
1.1 高登 Gaudin 方程
高登 Gaudin 方程为幂函数,形式为
式中:y为筛孔尺寸x的筛下累积产率,即筛下累积,%;x为筛孔尺寸,µm;Ag为与变量 (x,y) 选用单位有关的参数;k为与物料性质有关的参数,硬度大者k值大,硬度小者k值小。
对式 (1) 两边分别取对数,得
显然,在以lnx为横坐标,lny为纵坐标的坐标系内,lny与 lnx呈直线关系,k为直线斜率,lnAg为纵轴截距。
1.2 罗任-拉姆勒 Rosin-Rammer 方程
罗任-拉姆勒 Rosin-Rammer 方程是罗任-拉姆勒于 1934 年用统计方法整理破碎机和磨机产品得出的,形式为
式中:R为筛孔尺寸x的筛上累积,%;b为与破碎方式有关的常数;m为与物料性质有关的常数。
对式 (3) 两边取 2 次对数,得
式中:y为筛孔尺寸x的筛下累积产率,即筛下累积,%。
可得
将式 (5) 代入式 (4),可得
显然,在以 lnx为横坐标,lnln [100/(100 -y)]为纵坐标的坐标系中,lnx与 lnln [100/(100 -y)] 之间呈直线关系,m为直线斜率,lnb为纵轴截距。
2 粒度方程试验验证与分析
2.1 辊压试验方法
智能矿山重型装备全国重点实验室建立了水泥原料辊压机终粉磨工艺装备选型试验方法[7]。辊压试验机规格为φ420-100,辊子直径为 420 mm,辊面宽度为 100 mm,试验液压缸压力在 1.5~ 3.5 MPa,辊子外缘线速度为 0.46 m/s,试验入料粒度为 -13.2 mm。试验分为开路试验和闭路试验,闭路试验流程如图1所示。

图1 闭路试验流程Fig.1 Diagram of closed-circuit test flow
闭路辊压试验一般经过 3~ 4 次循环试验可以达到稳定状态,此时给料和排料粒度组成基本保持不变,排料中粗粒级相对减少,物料粒度分布范围变窄。
2.2 辊压产品粒度分析方法
辊压产品的粒度分析以干法、套筛的形式进行,由小到大筛孔尺寸为:0.080、0.106、0.125、0.150、0.200、0.300、0.425、0.600、0.850、1.180、1.700、2.360、3.000、5.000、6.700、9.500 和 13.200 mm,共 17 个粒级。由于辊压过程中可能形成料饼,为避免料饼对筛分结果的影响,在粒度筛分前,先对样品中的料饼进行了打散处理。同时在筛分过程中执行达到筛分终点的原则[2],以确保筛析结果能准确反应辊压产品的粒度分布,并为后续对不同条件下的试验结果进行对比提供了统一基准。
2.3 G 方程式和 RR 方程式验证与分析
某水泥原料辊压试验开路辊压中心料 A2C、开路辊压边缘料 A2S 以及闭路稳定产品中心料 B4C 的筛分粒度分析数据如表1 所列。
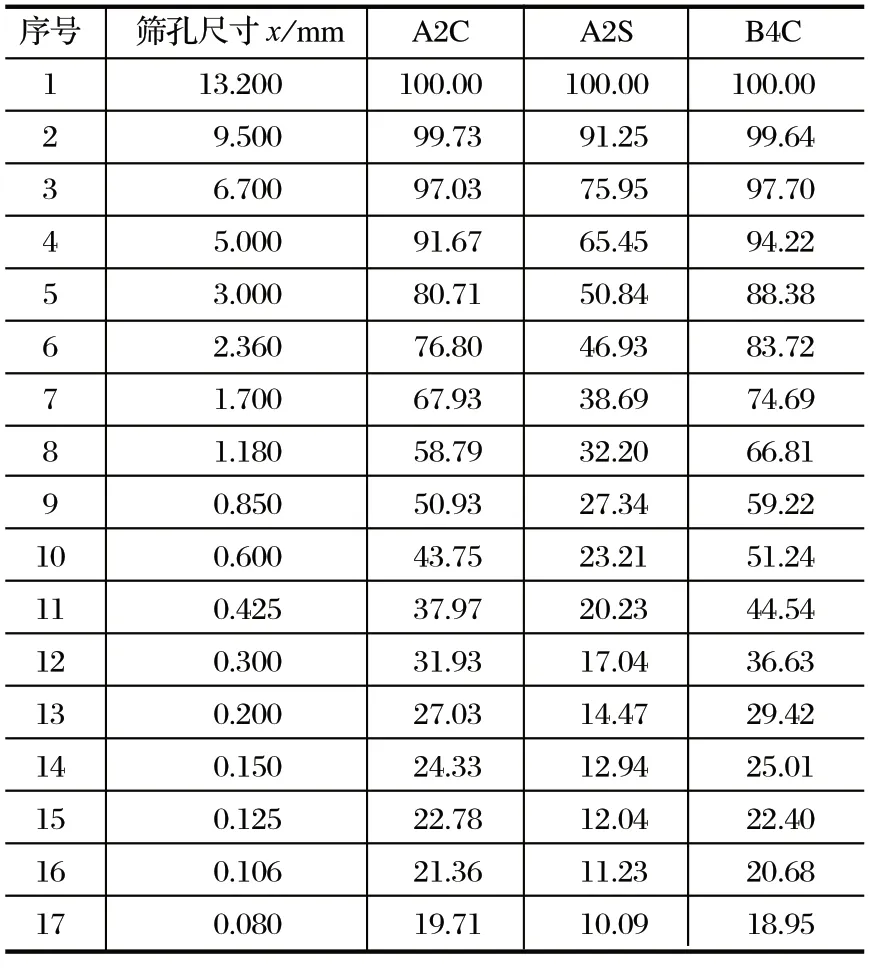
表1 某水泥原料辊压样品粒度筛分数据Tab.1 Particle size screening data of a cement raw material rolling sample
根据式 (2),由表1 数据分别计算出 17 个筛孔尺寸x相应 lnx和筛下累积y相应的 lny,在 Excel 中以 lnx为x数组,lny为y数组,利用最小二乘法原理,计算 G 方程式参数k、Ag,获得 3 个样品的 G 方程式。同理,根据式 (6),以lnx为x数组,lnln [100/(100 -y)] 为y数组,利用最小二乘法原理,计算 RR方程式参数m、b,求得 3 个样品的 RR 方程式,两个方程式回归结果如表2 所列。

表2 G 方程式和 RR 方程式回归结果Tab.2 Regression results of G equation and RR equation
由表2 G 方程式和 RR 方程式,计算不同筛孔尺寸x对应的拟合值Y,然后与表1 中的实际筛分值y进行比较,计算筛分值y与拟合值Y的差值,即为残差s,以残差平方和∑s2来判断方程式的拟合精度,残差平方和∑s2越小认为方程式越优越。
针对开路辊压中心料 A2C、开路辊压边缘料 A2S以及闭路稳定产品中心料 B4C,应用 G 方程式和 RR方程式进行拟合,得到残差分布图,结果如图2~ 4所示。
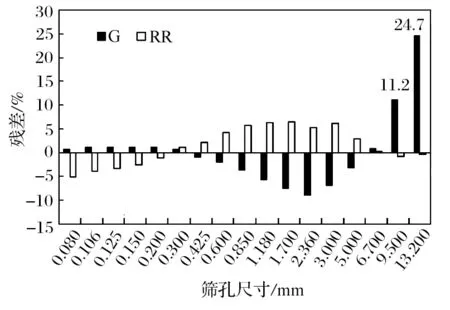
图2 中心料 A2C 各粒级残差分布Fig.2 Residual distribution of each particle size of central material A2C
由图2 可以看出:采用 G 方程式进行中心料A2C 粒度分布的拟合,13.200、9.500 mm 粒级残差较大,分别达到 24.7% 和 11.2%,从而导致残差平方和增加到 988.7,而 RR 方程式残差平方和较小为271.4;但在 0.080 到 0.300 mm 区间内,RR 方程式的残差明显大于 G 方程式;在 0.300 到 6.700 mm 区间内,RR 方程式的残差也明显大于 G 方程式。对中心料 A2C 而言,不论是 G 方程式,还是 RR 方程式,其拟合误差均较大,没有实际使用价值。
由图3 可以看出:采用 G 方程式进行边缘料 A2S粒度分布的拟合,G 方程式各粒级残差较小,残差最大值为 4.3%,残差平方和为 30.6,远小于 RR 方程式残差平方和 639.4。边缘料可以被认为是类似于破碎机的破碎产品。所以对于边缘料的拟合,G 方程式拟合精度较高,反映了 G 方程式对破碎产品进行拟合是可行的。

图3 边缘料 A2S 各粒级残差分布Fig.3 Residual distribution of each particle size of edge material A2S
由图4 可以看出:采用 RR 方程式进行稳定中心料 B4C 粒度分布的拟合,RR 方程式各粒级残差明显较小,残差最大值为 4.1%,RR 方程式残差平方和为50.49,远小于 G 方程式残差平方和为 2 118.8。对辊压闭路稳定产品而言,RR 方程式较优。
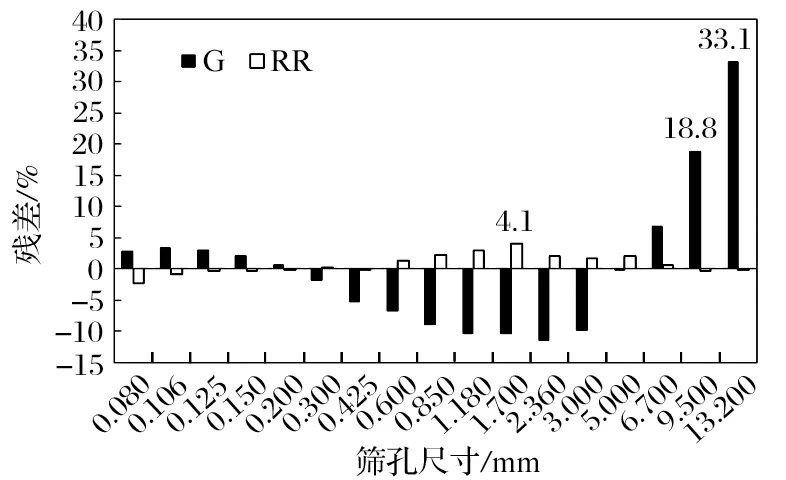
图4 稳定中心料 B4C 各粒级残差分布Fig.4 Residual distribution of each particle size of stable central material B4C
综观图2~ 4 可知,存在一个共性,即在 0.080到 0.300 mm 粒度范围内,两种方程式拟合残差都较小,但在拟合的粒度区间扩展到 13.200 mm 后,两种方程式拟合的残差都大幅增加。分析式 (2) 和式 (6),参数k和m均为定值,如果粒度分布曲线的斜率变化较小,回归精度必然很高,但辊压产品粒度分布曲线的斜率会随筛孔尺寸x不断变化,在以 lnx为横坐标,lny为纵坐标的直角坐标系中,辊压产品的粒度分布曲线大多呈现为上凸形状。对于闭路稳定产品的粒度分布曲线更为明显,表现为由分级筛位置向较粗方向上的曲线斜率明显增加,然后在达到粒度上限时趋于平缓,甚至为零。
RR 方程式中,开路辊压中心料样品 A2C、开路辊压边缘料样品 A2S 以及闭路稳定产品中心料 B4C,不同筛孔尺寸x的斜率变化如图5 所示。
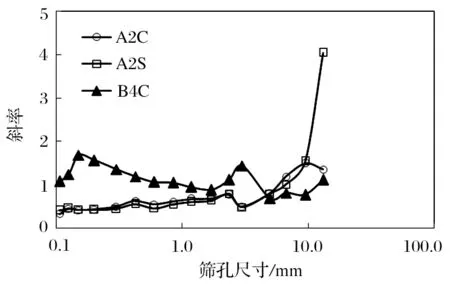
图5 RR 方程式中不同筛孔尺寸的曲线斜率分布Fig.5 Curve slope distribution of different screen sizes in RR equation
综合分析,在方程式中引入描述筛分曲线不同位置斜率的参数有可能是提高方程拟合精度的有效办法,由于 RR 方程进行了两次取对数,对平滑斜率变化更有利,故在 RR 方程式中引入斜率修正参数进行尝试。
在RR 方程式中引入参数M和N,将原方程式中的参数m变为一个与筛孔尺寸x有关的函数,关系如式(7)所示。
将式 (7) 代入式 (3),可得新 RR 方程式
对表1 粒度分布数据重新进行拟合分析,计算参数b、M、N,得到 3 个样品的粒度特性回归方程式如表3 所列。

表3 新 RR 方程式回归结果Tab.3 Regression results of new RR equation
由表3 数据,计算新 RR 方程式拟合的筛下累积Y,并与实际筛分值y做差,计算新方程式各粒级残差s,残差s分布及与修正前残差的比较如图6~ 8 所示。
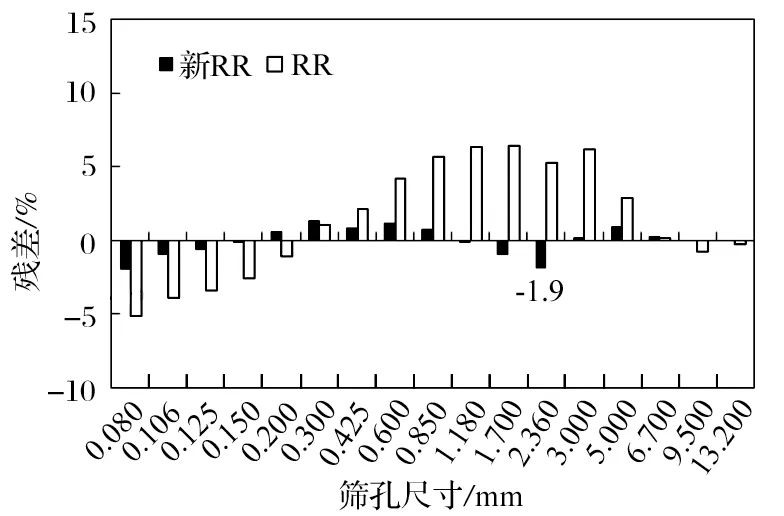
图6 新 RR 方程 A2C 各粒级残差分布Fig.6 Residual distribution of each particle size of A2C in new RR equation
由图6 可以看出:利用新 RR 方程式进行拟合,在 0.080 到 13.200 mm 整个筛分区间上,各粒级残差都很小,残差最大值为 1.9%,残差平方和∑s2为 15.23;而原 RR 方程式残差平方和 ∑s2为271.4,新 RR 方程式的拟合效果明显较好。
由图7 可以看出:利用新 RR 方程式进行拟合,在 0.080 到 13.200 mm 整个筛分区间上,各粒级残差都很小,残差最大值为 2.0%,残差平方和 ∑s2为9.91;而 RR 方程式残差平方和∑s2为 639.4,新 RR方程式的拟合效果明显较好。
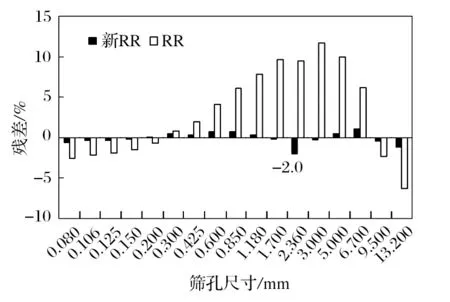
图7 新 RR 方程 A2S 各粒级残差分布Fig.7 Residual distribution of each particle size of A2S in new RR equation
由图8 可以看出:利用新 RR 方程式进行拟合,在 0.080 到 13.200 mm 整个筛分区间上,各粒级残差都很小,残差最大值为 1.2%,残差平方和∑s2为6.2;而 RR 方程式残差平方和∑s2为 50.49,新 RR 方程式的拟合效果明显较好。
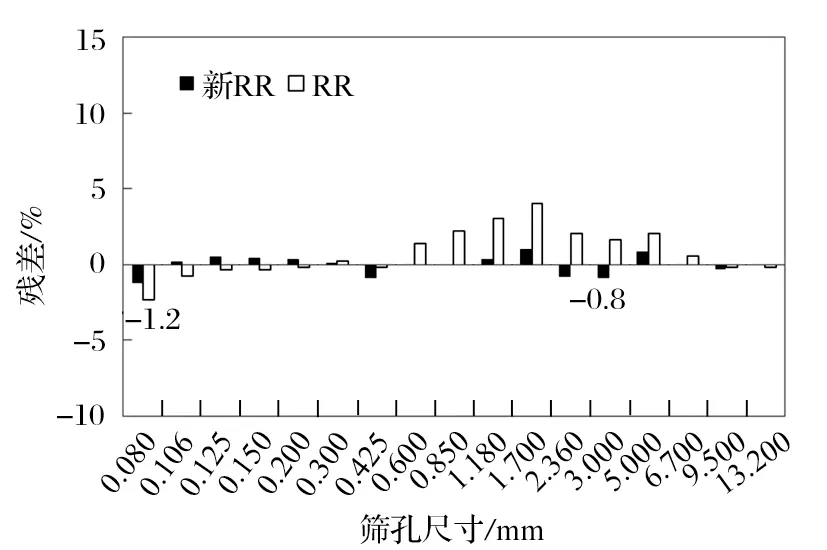
图8 新 RR 方程 B4C 各粒级残差分布Fig.8 Residual distribution of each particle size of B4C in new RR equation
由图6~ 8 可知,新 RR 方程的残差明显减小,为进一步确认新 RR 方程式的可靠性,对数据库中的17 组辊压数据均以新 RR 方程式进行回归计算,并与筛分数据进行对比,结果如图9 所示。
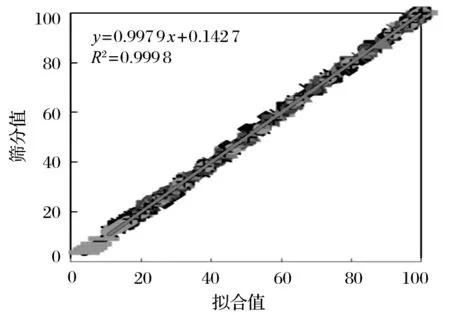
图9 新 RR 方程式拟合值与筛分值对比Fig.9 Comparison between fitting value and screening value of new RR equation
由图9 可以看出,新 RR 方程式回归结果与实际筛分结果非常接近,于是认为新 RR 方程式是可以作为水泥原料辊压产品粒度分布的回归方程式。
3 结语
(1) 在 RR 方程中引入描述粒度曲线斜率的参数M、N,将原固定斜率变为一个与筛孔尺寸有关的函数,方程的拟合精度明显提升,能够较为准确描述水泥原料辊压产品开路中心料、开路边缘料以及闭路稳定产品中心料的粒度分布,是理想的方程形式。在Excel 软件中利用规划求解功能,可以方便地进行参数b、M、N的计算,从而确定粒度分布方程。
(2) 通过粒度分布方程可以求得任意x值对应的筛下累积y,尤其对于获得较难筛分的小粒级筛下累积数据极为便捷。
