基于改进MIP模型的铁路牵引供电系统维护决策优化
2023-12-29邱实伍定泽王卫东胡文博王劲
邱实 ,伍定泽 , ,王卫东 ,胡文博 , ,王劲
(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 中南大学 轨道交通基础设施智能监控研究中心,湖南 长沙,410075;3. 中南大学 重载铁路工程结构教育部重点实验室,湖南 长沙,410075;4. 宁波市轨道交通集团有限公司建设分公司,浙江 宁波,315100;5. 香港理工大学 国家轨道交通电气化与自动化工程技术研究中心香港分中心,中国 香港,999077)
牵引供电系统主要由牵引变电所和接触网组成。目前。国内各铁路局检修维护规模庞大,覆盖面广,而维护人员和资源有限,传统的年度维护计划存在检维修频繁、维护成本较高的问题[1-2],如何在保证牵引供电系统高度可靠的同时,降低维护人员检修频率和维护成本,对于保证铁路安全运营具有重要的科研价值和工程意义。国内外学者对牵引供电系统维护及相关计划编制进行了研究,针对现有牵引供电系统维护模型进行更新,如陈绍宽等[3-6]提出了一种基于事故树分析的铁路牵引供电系统可靠度评价方法,该方法相较于传统评价方法具有用时少、误差低等优点,验证了可靠度评价方法在铁路牵引供电系统上的适用性;同时,对铁路牵引变电所和接触网的维护计划进行了分析优化研究,提出了基于随机寿命模型的通用软件工具和基于系统可靠度分析的牵引接触网维修计划调整方法。陈民武[7]在采用GO 法分析牵引供电系统可靠度的基础上,采用离散粒子群算法设计了维修计划优化仿真程序。黄俊歆等[8]利用混合整数规划法求解露天矿生产计划编制问题,极大减少了求解整数变量数量。毛道晓等[9]提出了越库中心选址的混合整数规划模型,并分别利用lingo算法求问题的精确解,利用2种启发式算法求问题的近似最优解。实验结果表明启发式算法的解接近于精确解,证明了启发式算法的有效性。XU等[10]将固定间隔的预防性维护和预测性维护相结合,并应用于年度接触网检修规划,提出了一种基于混合整数编程和启发式方法的决策支持模型。王玘[11]使用网络分析方法建立了决策模型,对牵引供电系统进行主动决策维护。徐学平等[12]从接触网的状态检修角度出发,建立了基于时变可靠度区间的接触网维护计划编制模型。刘志龙等[13]从维护成本角度出发,提出了一种基于故障率的效费比分析方法,用于地铁车辆预防性维护,对设备的最佳预防更换时机进行决策。BUDAI等[14]提出了一种铁路线路预防性养护维修计划编制模型,在已知线路养护维修任务及其周期的前提下,通过算法优化调整任务排班,集中安排,以减少占道时间,降低故障相关费用。郭然等[15]以费用最小化为目标提出了基于整数规划的铁路养护维修计划优化模型,考虑多条铁路线路内维护资源情况,验证了启发式算法的仿真优化的可行性。卢睿等[16]为了解决维护数据在流转过程中组织架构和数据安全性问题,从维护数据优化角度出发,提出了基于区块链技术的铁路四电信息共享框架。陈雍君等[17]对高铁四电建设工程建设方、设计方和施工方三方之间信息共享演化博弈行为进行研究,构建了单目标三方博弈收益矩阵以分析不同因素的变化对演化路径的影响。林熹东等[18]通过对牵引供电设备施工风险源及其等级进行划分,提出了基于贝叶斯BWM-VMEA 组合模型的优化权重分析方案。这些研究解决了部分维护数据的传递路径和维护权重划分的问题。为了在牵引供电系统的维护成本和部件可靠度之间取较大效费比,本文作者在不考虑铁路其他工种排班的前提下,对接触网系统和牵引变电所系统的可靠度进行建模,在此基础上构建考虑可靠度效比的牵引供电综合系统年度维护优化模型。
1 优化模型
1.1 问题描述与假设
牵引供电系统维护计划由各铁路局和供电段共同制定,通过对牵引变电所和接触网进行检测、分析诊断、质量评价和鉴定,制定详细的年度维护计划和月度维护计划。目前,铁路上牵引供电系统维护坚持“预防为主、重检慎修”的方针,按照“定期检测、状态维修、寿命管理”的原则,在列车运行时间段通过局部检查,对牵引变电所和接触网的外观、绝缘部件状态、外部环境及电力机车、动车组取流情况进行目视检查。在天窗时间内采用断电或带电方式对牵引变电所和接触网相关部件进行检测、维修及更换,如图1所示。

图1 不同时间段检维修事项Fig. 1 Inspection and maintenance matters in different time periods
随着牵引供电部件役龄和检维修次数增加,部件的可靠度和使用性能会出现一定规律的衰退,为了更好地进行维护,通常基于部件的性能阈值将维护任务分成更换、维修、检查3类,如图2所示。为了尽可能发挥部件的使用价值,在部件维护过程中比较计划性维护和预防性维护的可靠度和效费比,根据故障状态不同,将牵引供电系统分成计划维修部件和可靠度预维修部件。考虑到牵引供电系统部件的可靠度概率分布大多符合威布尔可靠度分布,本文从时间、可靠度、效费比3个方面进行牵引供电系统年度维护决策优化。
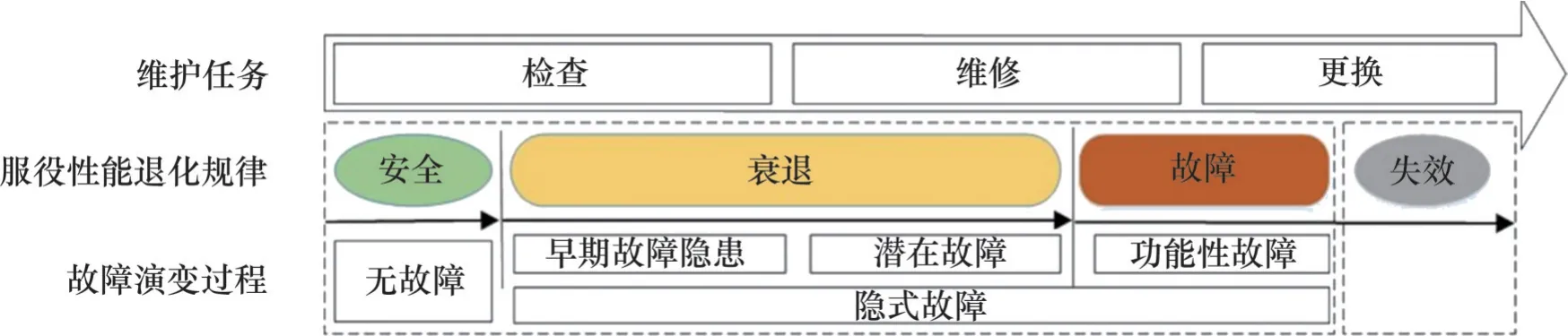
图2 牵引供电系统部件维护任务对应的服役性能退化规律和故障演变过程Fig. 2 Service performance degradation pattern and fault evolution processes corresponding to maintenance tasks of traction power supply system components
根据已建成的铁路运营管理经验,牵引供电系统维护的基层机构(工班和电车间)设置密度越大,机构间的距离越短,部件维护的效率和可靠度就越高,相互协作能力越强,但容易导致维护成本成倍增加,造成资源浪费,如何合理根据部件状态和成本因素安排牵引供电系统维护计划是本文的研究重点。为了简化维护计划关系,本文只考虑牵引供电系统下的牵引变电所和接触网系统。模型假设如下:
1) 在系统初始状态下,部件的状态为全新状态。
2) 系统在月计划内存在最低可靠度约束。
3) 由于维护任务均安排在天窗时间进行,暂不考虑停机时间对系统退化的影响。
1.2 故障概率模型及故障树分析
目前,常用的可靠度概率分布主要是威布尔分布、指数分布、正态分布和泊松分布等[16]。本文研究牵引供电系统部件在年度维护过程中的时间相关故障模型,采用威布尔分布对预维护的部件故障率建模,采用指数分布对计划维修的部件故障率建模。威布尔分布故障率函数λ(t)和可靠度函数R(t)的定义式分别见式(1)和式(2)。式(1)和(2)中,β为形状参数,决定故障率函数的增减趋势;θ为特征寿命,影响分布函数的均值和广度;t为时间。
变电所和接触网这2个子系统中符合部件可靠度分布的主要部件和参数如表1所示。

表1 供电分区内主要部件参数[5-7]Table 1 Main equipment parameters in the power supply subzone[5-7]
以牵引供电系统失效为研究对象,建立故障树模型,如图3 所示。图3 中,三角弧形为逻辑门,圆形为基本事件。所建故障树共由3 个或门、12 个彼此独立的基本事件组成,故障树顶事件定义为牵引供电系统不能正常运转,所假定的可靠度分布函数见表1。采用本文建立的故障树模型对牵引供电系统可靠度进行定性评价,描述系统各故障之间的内在联系,指出部件故障与系统故障之间的逻辑关系,结合各部件的可靠度分布模型对牵引供电系统可靠度进行定量评价,为MIP 模型提供牵引供电系统的可靠度和其他可靠度特征量,为计算和评估系统的可靠度提供定量依据。

图3 牵引供电系统故障树Fig. 3 Traction power system fault tree
1.3 MIP模型
本研究建立的基于可靠度效比的优化模型中具有连续变量、0-1决策变量,同时还包含非线性函数,属于混合整数非线性规划模型(mixed integer programming, MIP)[19]。
1.3.1 变量和集合参数
MIP模型主要变量、集合参数见表2~4。

表2 MIP模型集合参数Table 2 MIP model set parameters

表4 MIP模型决策变量Table 4 MIP model decision variables
1.3.2 双子系统耦合可靠度约束下的维护费用最小模型
牵引供电系统年度总维护成本P(c)包括接触网各部件和变电所在每一区间内维护(维修、更换和检查)成本和故障相关成本,即
式(4)和(5)构成了模型的可靠度约束条件,式(4)表示牵引供电部件在t时间段时平均可靠度不低于最小值,式(5)表示牵引供电系统可靠度在t时间段时不低于最小值。
式(6)为牵引供电系统工时条件约束,保证每个子系统的任务分配工时不超过最大使用工时,也不低于最小使用工时。
式(7)是天窗时间的约束条件,在所有天窗期,维护任务安排总时间不得高于该段维护期内的天窗时间。
式(8)表明牵引供电系统年度维护计划维修支出不超过预算。
1.4 分配流程和优化算法
1.4.1 分配流程
本文建立的基于MIP 的铁路牵引供电系统维护决策优化模型的求解算法流程如图4所示。第一步,输入牵引供电系统年度维护数据,主要包括各个部件的数量可靠性概率及寿命等数据,通过分类识别模块按照固定间隔维护策略和预维护策略对部件进行分类,将含有退化模型的部件依据退化模型得出全年各时间点发生故障的概率,对于一些不存在退化模型的部件采用线性换算法计算再次需要更换的概率。第二步,根据识别的维护任务进行分配,在维护规章和系统可靠度的约束下,用改进的退火算法对维护任务进行优化计算。第三步,通过计算结果分别分配接触网系统和牵引供电系统的维护任务,得到优化后的牵引供电系统年度维护计划。

图4 牵引供电系统年度维护计划优化算法流程Fig. 4 Optimization algorithm processes of traction power system annual maintenance plan
1.4.2 优化算法
启发式算法和精确算法在求解大规模调度问题时存在一定的局限性[20]。启发式算法可在可行范围内获得求解问题的较好解,但无法保障解的质量。精确算法的最大优点是可以为问题寻得最优解,但随着问题规模变大,计算量剧增。随着改进智能算法的引入,可克服启发式算法在全局搜寻最优解的不足。本文实验案例有16 种共计超过1 000 项检修单元,计算难度和时间成本过高,为此,采用一种改进的模拟退火全局搜索算法,如图5所示,用于解决混合整数全局优化问题。该算法在标准的模拟退火算法中加入了特殊的截断程序,增加了可行点生成的随机性,打破了在接触网和变电所各自系统内及年度维护计划各月份内搜索最优解的局域限制,提高了搜索全局最优解的可能性。

图5 基于模拟退火算法的牵引供电系统年度维护计划求解流程Fig. 5 Annual maintenance plan solving processes for traction power supply system based on simulated annealing algorithm
2 案例分析与算法实现
2.1 案例背景及数据
某铁路局下属运营维修段包括6个接触网综合维修车间和1个变配电修试队。选择接触网系统和变电所系统共16 种部件的维修和检查任务,某铁路局运营维修段年度部件故障数量如表5所示,表中数字表示某部件在某月的故障数量。

表5 某铁路局运营维修段年度部件故障数量Table 5 Annual number of component failures in a railroad bureau operation and maintenance section
2.2 优化结果
通过优化算法得出该铁路段牵引供电系统年度维护费用、故障相关费用、总成本及总工时,如表6 所示。优化算法所得提升结果见表7。从表7可见:采用本文优化模型得到的维修费用相较于现有维护计划费用减少了7.94%,故障相关费用减少了8.03%,总成本降低了7.97%,总维护工时降低了11.18%。这说明通过本文的优化算法模型减少了故障总成本和总工时,合理分配了维护任务,降低了维护成本。

表6 不同月份不同解决方案的成本Table 6 Cost of different solutions for different months

表7 优化算法提升结果Table 7 Improvement results of optimize algorithms
由优化算法得出牵引供电系统各子系统可靠度如图6所示。从图6可以看出:在现有维护方案下,最初几个月份系统可靠度较低,在全周期(1~12月)内可靠度波动较大。然而,在应用优化算法后,随着维护任务不断增加,系统可靠度上下波动幅度较小,在全周期内系统可靠度较平均,其主要原因是该算法在各子系统可靠度的基础上进行维护任务分配,保持系统可靠度在一定阈值之上。

图6 现有方法和优化算法的可靠度对比Fig. 6 Comparison of reliability of existing methods and optimized algorithms
3 结论
1) 既有研究关于牵引供电系统年度维护计划优化方案通常涉及接触网系统和牵引变电所这2个子系统,为了降低模型复杂程度,大多将接触网系统或牵引变电系统作为相互独立系统进行研究。而接触网系统和牵引变电所系统的维护从本质上是相互联系、相互影响的,通过整体考虑可以更加全面提升铁路牵引供电系统维护管理体系的优化效果,且在模型构建方法和算法上是可行的。
2) 本文优化算法相较于现有算法,在稳步优化可靠度的基础上,更加合理安排年度维护计划,从维护费用、故障相关费用及工时三方面量化分析优化结果,减少了障总成本和总工时的同时,合理分配了维护任务,降低了维护成本。因此,本文所建立的基于可靠度效比的维护决策优化模型可行且有效。本文只考虑了铁路牵引供电系统的年度维护,并没有考虑通信、信号、车辆等方面的维护需求,因此,在未来的研究中,基于可靠度效比的全局优化算法,需考虑维护任务间的相互关系,提出铁路年度综合维护计划优化方案,探索不同因素对综合维护计划优化的影响。
