基于遗传算法的CRTS Ⅱ型无砟轨道简支梁桥纵向抗震简化模型
2023-12-29蒋丽忠钟不凡张云泰周旺保余建赵胤婷
蒋丽忠 ,钟不凡,张云泰,周旺保 ,余建,赵胤婷
(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 高速铁路建造技术国家工程实验室,湖南 长沙,410075)
中国现在拥有最大的高速铁路网[1]。其中,多条高速铁路线路跨越地震带,为保证公共财产和生命安全,高速铁路桥梁的地震响应一直是学术界的热点问题[2-3]。高速铁路桥梁-轨道系统结构复杂,运用精细的高速铁路桥梁模型BM(bridgetrack system model)会降低大样本数据以及参数分析的研究效率,为了快速获得精确的桥梁地震响应结果,有必要对BM进行合理简化。
为了提高模型计算效率,研究人员提出了许多简化方法。《铁路工程抗震设计规范》[4]建议不考虑轨道结构的约束效应将其质量进行析减,附加到主梁上。LI 等[5]开发了一种非线性S-P 弹簧系统,在模型边界处的每根钢轨切割处进行布置,用于模拟轨道系统所提供的纵向支撑。JIANG等[6]提出了一种单独研究目标结构,将边界相邻结构简化为弹簧系统的简化方法。GUO 等[7]通过主梁力-位移曲线将整个轨道结构简化为连接相邻主梁的非线性弹簧。张永亮等[8]将所有的钢轨、轨道板和底座板视作一个整体,通过弹性梁柱单元来模拟。LI等[9]在简化时只保留钢轨而移除轨道结构其他构件。ÜLKER-KAUSTELL 等[10]将铁路桥梁系统假设为具有一定质量和刚度的门式框架结构。
上述研究有助于简化模型模拟高速铁路简支梁桥的地震响应,但简化模型中存在如下不确定性因素和误差:1) 边界条件的不确定性,如路基长度;2) 有限元网格划分质量差或单元过于简化所引起的误差;3) 有限元模型建模过程中进行的假设,如结构构件的刚性连接假设。这些因素会导致简化模型SM(simplified model)不能准确模拟BM地震响应结果。研究人员开始借助优化算法来获取合理的有限元模型结构参数。DENG等[11]基于梯度的优化算法提出一种多目标优化技术,对润阳悬索桥的初始多尺度模型进行更新,大幅度减少了全局最优解的搜索工作量。ZHU 等[12]结合响应面法和基于梯度的多目标优化方法对香港昂船洲斜拉桥的多尺度模型进行了修正,得到了全局最优解和相应的模型参数。
优化算法辅助能有效、快速地获得模型结构的合理参数,减少工作量,因此,为了建立高质量的SM,有必要借助优化算法辅助进行参数优化完成建模。利用优化算法更新有限元模型结构参数在许多结构中已有许多成功应用。LEVIN 等[13]使用模拟退火算法和遗传算法通过更新悬臂梁的质量和刚度来得到结构的固有频率。DENG等[11]结合响应面法和遗传算法,基于既有桥梁的现场试验数据对比并更新了模拟简支梁桥模型的5个材料参数。ZHANG 等[14]基于支持向量机的响应面法,并结合遗传算法对某扭转梁结构的有限元模型进行了更新。优化算法的高效和精确能为优化有限元模型结构参数提供帮助,但目前鲜有关于高速铁路桥梁复杂耦合效应结构模型参数优化的研究。
建立同时兼顾计算效率和计算精度的SM是保证快速获得桥梁地震响应精确结果的前提。为克服以往SM 的局限性,本文以CRTS II 型板式无砟轨道结构高速铁路梁桥为研究对象,基于轨道结构约束效应等效的设计原理,提出以等效弹簧模拟轨道约束效应的方法,建立考虑轨道结构纵联效应的SM,构建基于遗传算法的有限元模型结构参数优化框架,通过不断更新等效弹簧刚度使SM与BM的固有振型达到一致,从而获取SM等效弹簧最优刚度。从PEER 地震数据库中随机选择10条地震波,对标准5 跨SM 和BM 开展地震分析,对比有限元模型的地震响应计算时间以及计算结果,以验证SM的快速性及有效性。
1 有限元模型简化方法
CRTS Ⅱ型板式无砟轨道结构是中国高速铁路梁桥使用的标准化轨道结构之一,由纵向连续构件(钢轨、扣件和轨道板)以及层间连接构件(CA砂浆层、底座板、滑动层等)组成,精细的CRTS II型板式无砟轨道结构桥梁有限元模型单元数量众多,如图1所示。轨道结构的单元数量庞大,将导致有限元模型地震响应计算时间过长。对于传统有缝线路,钢轨不连续,梁轨相互作用小,甚至可以忽略[15]。无砟轨道为桥梁结构提供了一定的纵向刚度和约束[16],增强了高速铁路桥梁的整体性,使得桥梁成为一个弱耦合结构。研究表明,忽视轨道结构约束效应会产生不合理的桥梁地震响应结果[17-18],因此,合理简化轨道结构是提高SM计算效率和计算精度的关键。本文基于轨道约束效应等效的设计原理,提出BM抗震计算的简化轨道结构有限元模型,构建基于遗传算法的有限元简化模型参数优化框架,该框架流程如图2 所示,具体步骤如下:

图1 高速铁路简支梁桥有限元模型Fig.1 Finite element model of simply supported beam bridge of high-speed railway

图2 简化模型参数优化框架Fig. 2 Simplified model design and parameter optimization framework
1) 建立BM,根据设计原理对BM 进行合理简化。
2) 确定优化预期目标,将优化预期目标作为判断简化模型参数完成优化的依据,根据优化预期目标构建目标函数,确定SM优化参数及其约束条件。
3) 利用优化算法更新优化参数,并更新SM。
4) 提取BM 以及SM 用于构建目标函数的指标,计算优化参数对应的目标函数值。
5) 若目标函数值满足优化预期目标,则执行步骤6),若不满足,则返回步骤3)。
6) 对BM以及SM开展地震响应时程分析,提取模型地震响应计算结果,计算地震响应结果误差。
7) 若结果误差满足要求,则SM建立完成;若不满足,则返回步骤2),重新确定优化预期目标。
该框架的实现需要定义优化参数、目标函数和优化算法。
1.1 优化参数
优化参数决定整个优化程序的质量。选择的优化参数在更新后需要体现BM的动态特性,准确模拟BM轨道结构的约束效应。优化参数的取值具有不确定性,且对结构预期目标结果的影响具有敏感性。
为了有效模拟轨道结构约束效应并同时降低有限元模型的复杂性,这里提出一种等效弹簧模拟轨道结构约束效应的方法,将轨道结构简化为连接相邻主梁的等效弹簧,等效弹簧刚度取值是否合理决定了等效弹簧模拟轨道结构约束效应是否有效。有限元简化模型如图3 所示,其中,k为等效弹簧刚度,i为弹簧编号。

图3 有限元简化模型Fig. 3 Finite element simplified model
CRTS Ⅱ型板无砟轨道结构具有纵联效应,因此,在地震作用下,高速铁路桥梁结构的纵向运动将受到路基系统的约束效应,不同位置的桥跨将受到不同程度的路基约束效应;轨道结构中剪切钢筋、剪力齿槽和侧向挡块的位置不对称;主梁两侧固定支座和滑动支座的力学特性存在差异,这些因素都会导致桥梁不同位置处等效弹簧的刚度产生差异,因此,获得不同位置的等效弹簧最优刚度具有重要工程实用价值,而其参数存在不确定性,为此,本文将等效弹簧刚度设置为优化参数。
1.2 目标函数
目标函数可表征目标指标和模拟指标之间的差异。指标的选取不仅要考虑优化参数更新对该指标的敏感性,而且要衡量获取该指标的难易程度。在地震作用下,研究人员提取地震响应结果作为指标,利用结果差异构造目标函数,对桥梁参数进行优化。这种方式优化效率较低。本文优化预期目标是使BM 与SM 的固有振型达到一致,鉴于固有振型对高速铁路梁桥纵向地震响应的贡献最大,BM 与SM 的固有模态越接近,模型地震响应结果误差越小。为了量化固有振型,有必要提取关键的模态数据作为指标构造目标函数。本文选取的目标指标为BM的固有频率以及相邻主梁振型位移比,模拟指标为SM的固有频率以及相邻主梁振型位移比,利用2个模型固有频率的相对误差与相邻主梁振型位移比的相对误差之和来构造目标函数,该指标避免在搜索全局最优解时反复迭代结构地震响应结果,提取易获得的模态信息,有效提高搜索等效弹簧最优刚度的效率。定义固有频率相对误差δf与固有振型相邻主梁位移比相对误差δD为:
其中:
式中:下标b、s 分别表示BM、SM;f为固有频率;D为固有振型下相邻主梁位移比;di为固有振型下第i跨主梁位移。则本文的目标函数可表示为
可以看出,y越小,则SM 与BM 的模态数据相对误差越小,固有振型越接近,SM等效弹簧模拟BM轨道约束效应效果越好。当y等于或近似等于0时,定义当前等效弹簧刚度为最优。
1.3 优化算法
优化算法是用于最小化目标函数的算法。本文采用遗传算法来优化SM等效弹簧刚度。遗传算法[19]是基于种群的随机搜索算法,是一种通过模拟自然进化过程搜索最优解的方法,能够在许多局部极小值中找到全局极小值。遗传算法流程如图4所示。

图4 遗传算法流程图Fig. 4 Optimization process of the GA method
为了搜索全局最优方案,遗传算法在搜索范围内随机产生一个初始种群,种群由许多不同的个体(优化参数的集合)组成,个体中的参数用于更新简化模型并开展模态分析。初始种群产生后,计算该种群每个个体的目标函数值,为子代创建3种类型个体(精英个体、交叉个体、变异个体)。
精英个体指的是种群中适应度高的个体,每一代种群的精英个体会被保留成为下一代种群个体。式(4)为本文遗传算法的目标函数,由于本文目的是得到BM与SM模态信息误差的最小值,故在精英个体的选择过程中,目标函数值小的个体将视为精英个体被保留。交叉个体指的是将上一代种群中成对的个体进行信息相互交叉处理,从而产生新一代个体。成对个体之间发生交叉操作的可能性由交叉概率pc来控制。变异个体指的是种群中每个个体对应的存储信息在随机位置发生随机变异。个体发生变异操作的可能性由变异概率pm来控制。
2 算例分析
2.1 高速铁路桥梁模型
选取8 度地震区内1 座CRTS Ⅱ型板式无砟轨道结构的高速铁路简支梁桥为研究对象,高速铁路桥梁-轨道系统由桥梁结构和轨道结构组成。桥梁结构由主梁、支座和桥墩组成。主梁跨度为32 m,采用箱型截面,桥墩高度为20 m,采用圆端型截面,主梁及桥墩横截面分别如图5和图6所示。CRTS Ⅱ型板式无砟轨道结构由钢轨、轨道板、底座板、扣件、CA 砂浆层、滑动层、剪力齿槽、剪切钢筋、侧向挡块等构件组成。钢轨、轨道板和底座板是纵向连续构件。扣件、CA砂浆层、滑动层是层间连接构件。剪力齿槽布置在固定支座的上方,剪切钢筋布置在梁缝两端的底座板和轨道板之间,侧向挡块布置在桥面板上轨道结构的两侧。

图5 主梁横截面示意图Fig. 5 Cross-section of grider

图6 桥墩横截面示意图Fig. 6 Cross-section of pier
采用ANSYS 有限元软件建立高速铁路桥梁-轨道系统的有限元模型。简支梁的跨数取为5。钢轨、轨道板、底座板、主梁和桥墩使用BEAM189单元模拟,单元长度设置为0.645 m。轨道板的截面长×宽为2.55 m×0.20 m,底座板的截面长×宽为2.75 m×0.20 m。扣件、CA砂浆层、滑动层、侧向挡块、剪力齿槽、剪切钢筋等连接构件使用COMBIN14 单元建模,根据文献[20-23],各构件在不同方向上的计算刚度见表1。扣件、CA 砂浆层、滑动层使用间隔为0.645 m 的等间距弹簧模拟,侧向挡块的纵桥向以及横桥向的刚度均为1.2×104kN/m,竖直方向上的刚度取1.38×109kN/m,32 m 简支梁桥侧向挡块的间距为5.74 m,路基段侧向挡块的间距一般为8.00 m,因此,在有限元模型中,简支梁上每间隔9 个扣件布置1 个侧向挡块,路基段上间隔12 个扣件布置1 个侧向挡块,其余弹簧按照桥梁中实际位置布置。本文不考虑各构件的刚度折减。基于ZHANG[24]对桥梁边界特性的研究结果,路基长度取90 m,摩擦板长度设置为50 m。结构阻尼采用瑞利阻尼,阻尼比为0.05。

表1 连接构件弹簧刚度Table 1 Stiffness of interlayer componentskN·m-1
2.2 简化模型
由简化方法(轨道结构简化为等效弹簧)可知,有限元SM的桥梁结构信息与BM的桥梁结构信息完全相同,等效弹簧使用COMBIN14 单元模拟,刚度参数由框架优化得到。本文采用ANSYS进行桥梁模态分析,使用MATLAB 程序编制的遗传算法进行参数优化。软件实施的具体流程是:首先,MATLAB产生简化模型参数(等效弹簧刚度)并分配到ANSYS 的简化模型,对BM 和SM 开展模态分析;然后,将模态信息结果发送到MATLAB 进行结果评估;最后,将参数更新分配到ANSYS,直到满足优化收敛性准则为止。本文简化模型等效弹簧最优刚度见表2。

表2 简化模型等效弹簧最优刚度Table 2 The optimum stiffness of equivalent spring of simplified model
2.3 地震动记录选取
进行结构地震分析时首先要对地震动记录进行选择。本文从太平洋地震工程研究中心数据库(PEER)中选取10条加速度波(编号分别为E1、E2、E3、E4、E5、E6、E7、E8、E9、E10),见表3。参照《铁路工程抗震设计规范》[4],抗震设防烈度为8度,设计地震峰值加速度为0.2g,考虑剪切波速为250~500 km/s的II类型场地,调整记录峰值加速度。有限元模型输入地震波的持续时间取15 s。
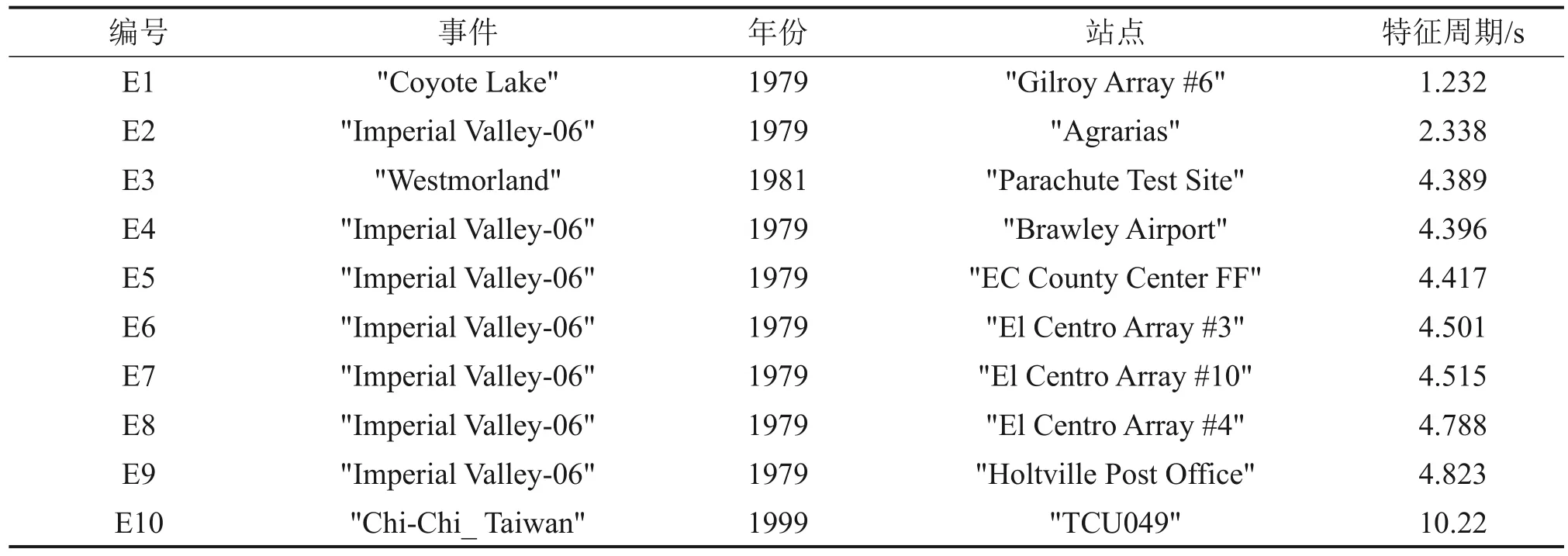
表3 地震动记录Table 3 Ground motions record
以往的研究表明,高速铁路桥梁系统在横向的抗震性能会比纵向的抗震性能更加优越[25]。桥墩纵向刚度较低,在纵向上也更容易被破坏[26]。桥梁的一阶纵向模型振动对大部分地震响应都有贡献[27],因此,本文的地震输入方向选为纵向。
2.4 简化模型有效性验证
合理的SM必须提高计算效率并保证计算结果的精度。与BM相比,SM的节点和单元数量减小,节点及单元数量的对比结果见表4。输入选定的地震动,获得不同模型所需的计算时间,见表5。从表5 可见:SM 的单元简化率为97%,节点简化率为90%;BM的计算时间是SM的8~10倍,这表明SM降低了建模难度,同时提高了计算效率。

表4 数值模型单元及节点数量对比Table 4 Comparasion of element and node information of numerical models

表5 不同模型地震分析的计算时间Table 5 Calculation time of seismic analysis with different modelss

图7 最大地震响应相对误差δRFig. 7 Relative errors of seismic responses δR

图8 中跨主梁位移时程曲线对比Fig. 8 Comparisons of time history seismic responses of middle span
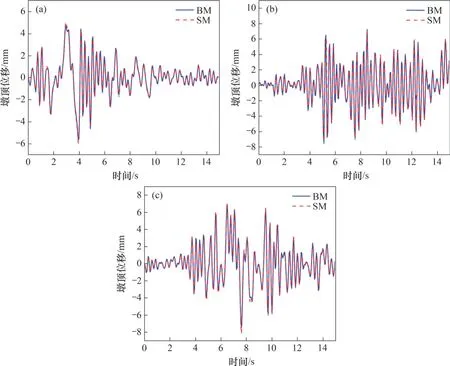
图9 中墩墩顶位移时程曲线对比Fig. 9 Comparison of time history seismic responses of middle pier
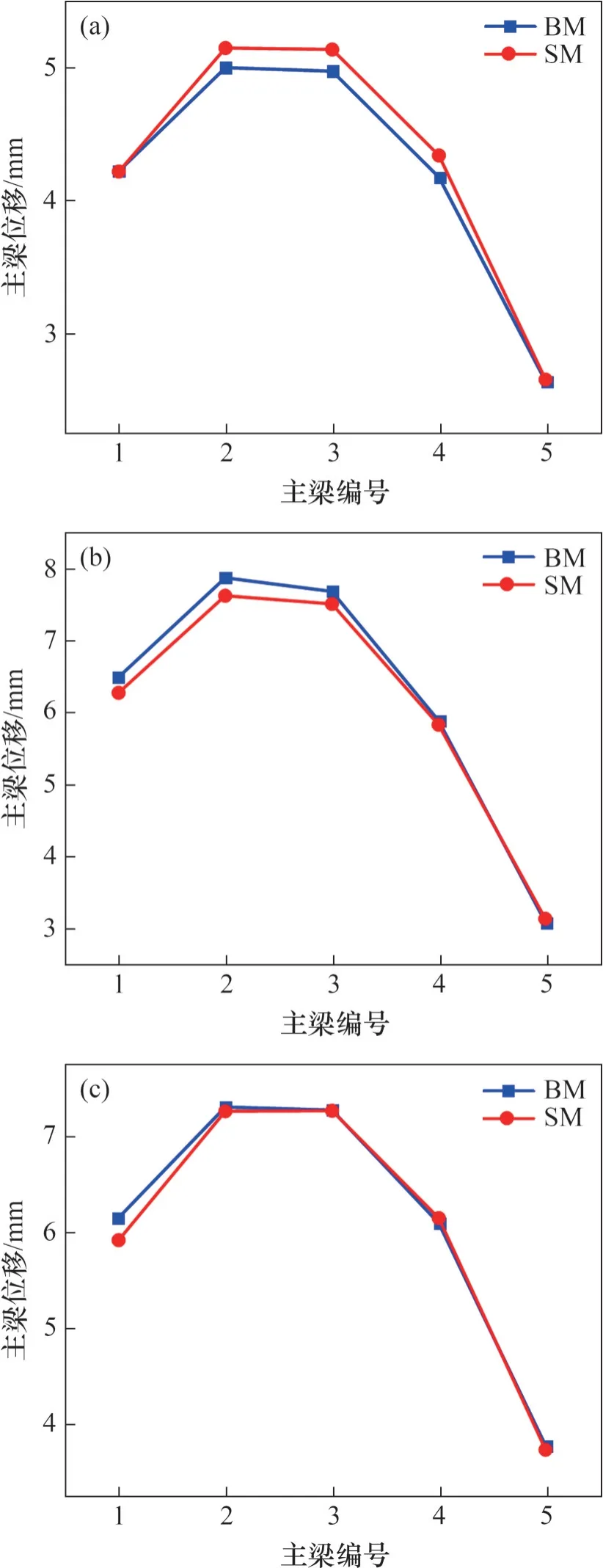
图10 主梁位移包络图Fig. 10 Envelope diagrams of displacement of girder
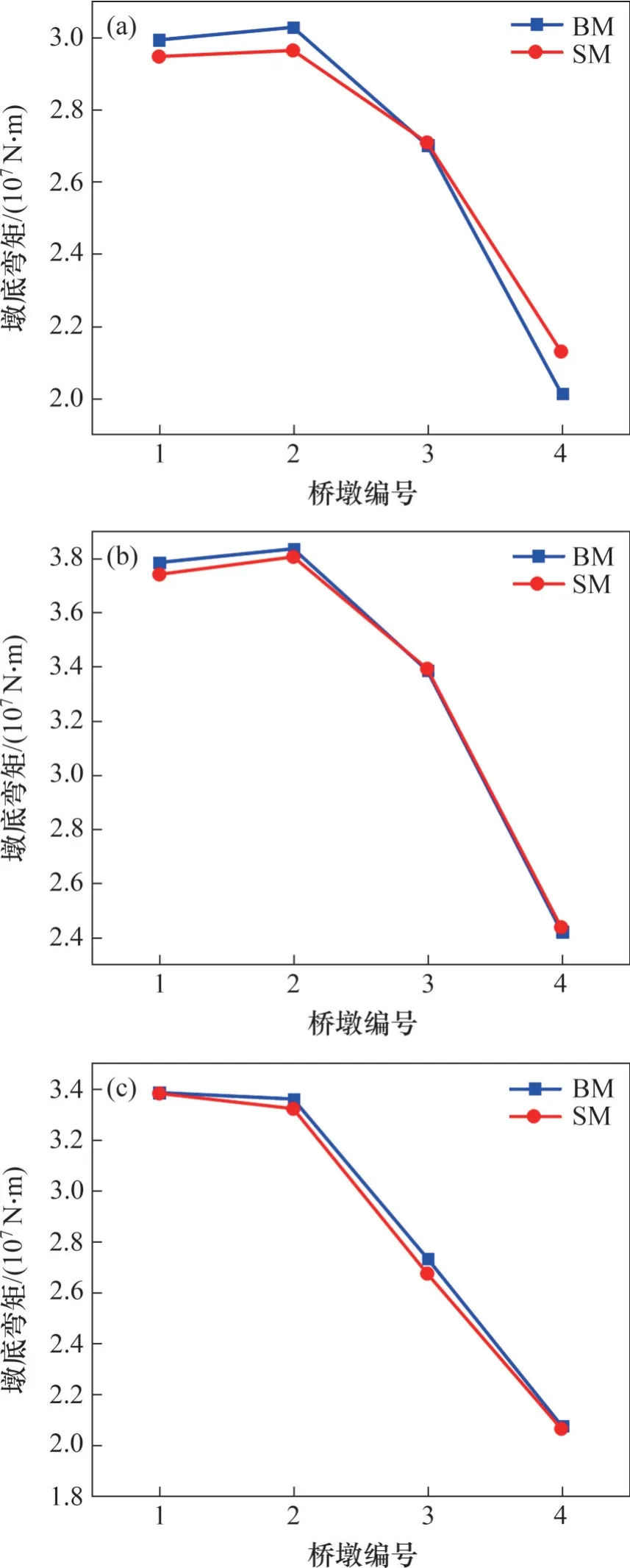
图11 墩底弯矩包络图Fig. 11 Envelope diagrams of bending moment of bottom of pier
从图7~11可见:BM和SM地震响应结果的相对误差平均值约为3%,最大相对误差不超过5%;SM 和BM 的时程曲线和包络图无论是峰值还是形状都较吻合。综上可知,SM保证了每一跨结果的精度,能正确反映出轨道约束对每一桥跨的地震响应的影响,SM 能有效模拟BM 在地震作用下的地震响应。
3 结论
1) SM抗震计算的有效性得到了验证。无论是时程曲线形状还是包络图分布,SM地震响应计算结果与BM较吻合,最大相对误差不超过5%。
2) SM 抗震计算的快速性得到了验证。SM 的单元简化率达到97%,节点简化率达到90%,BM的地震响应计算时间为SM计算时间的8~10倍。
3) 有限元模型结构参数优化框架可用于SM等效弹簧刚度参数的优化,以模态信息误差作为SM参数优化的目标函数是合理的,遗传算法获得的最优等效弹簧刚度可有效模拟轨道结构对桥梁结构的纵联约束作用。
